Basal conditions and glacier motion during the winter/spring transition, Worthington Glacier, Alaska, U.S.A.

Abstract

Observations of the motion and basal conditions of Worthington Glacier, Alaska, U.S.A., during late-winter and spring melt seasons revealed no evidence of a relationship between water pressure and sliding velocity. Measurements included borehole water levels (used as a proxy for basal water pressure), surface velocity, englacial deformation, sliding velocity, and time-lapse videography of subglacial water flow and bed characteristics. The boreholes were spaced 10–15 m apart; six were instrumented in 1997, and five in 1998. In late winter, the water-pressure field showed spatially synchronous fluctuations with a diurnal cycle. The glacier’s motion was relatively slow and non-cyclic. In spring, the motion was characterized by rapid, diurnally varying sliding. The basal water pressure displayed no diurnal signal, but showed high-magnitude fluctuations and often strong gradients between holes. This transition in character of the basal water-pressure field may represent a seasonal evolution of the drainage system from linked cavities to a network of isolated patches and conduits. These changes occurred as the glacier was undergoing a seasonal-velocity peak. The apparent lack of correlation between sliding velocity and water pressure suggests that local-scale water pressure does not directly control sliding during late winter or early in the melt season.

1. Introduction

A central component of glacier dynamics is the process whereby basal ice becomes partially decoupled from the bed, causing sliding motion. Often, half of the motion of a wet-based (temperate) glacier is due to basal slip, and it is not uncommon for nearly all of a temperate glacier’s movement to result from sliding (Paterson, 1994). Likewise, surges and fast glacier flow phenomena are typically attributed to sliding processes (e.g. Kamb, 1987; Raymond, 1987; Kamb and others, 1994; Meier and others, 1994; Engelhardt and Kamb, 1998). Despite the established significance of glacier sliding, the difficulties associated with directly observing basal conditions have impeded understanding of this process.

Sliding of a temperate glacier over a rigid or “hard” bed entails complex processes involving interactions of basal ice, water at the base of the glacier, and the bed itself. Numerous studies have compared direct measurements of glacier motion with observations of the subglacial hydrological system (e.g. Iken and others, 1983; Kamb and others, 1985; Iken and Bindschadler, 1986; Kamb and Engelhardt, 1987; Hooke and others, 1989; Blake and others, 1994; Jansson, 1995; Raymond and others, 1995; Harbor and others, 1997; Iken and Truffer, 1997; Hanson and others, 1998). Yet, a predictable linkage between sliding velocity and measurable parameters of the hydrological system has been elusive. Spatial and temporal changes in water inputs, drainage-configuration responses to those inputs, and complex feedbacks between basal processes and ice dynamics all confound the relationship between glacier movement and hydrology (Kamb, 1970). An important aspect of the problem is that models of subglacial water flow suggest that water pressure and water storage increase jointly (Lliboutry, 1968; Iken, 1981; Fowler, 1987; Kamb, 1987). Individual observations, however, have detected correlations between velocity and either pressure or storage, but not with both (Fountain and Walder, 1998).

This study adds to the empirical linkages between subglacial conditions and glacier movement. We describe the results of simultaneous monitoring of multiple parameters related to the problem: surface velocities, internal deformation, basal sliding velocities, borehole water levels, and direct observations of basal conditions. This range of information enables the sliding velocity to be examined with respect to the conditions present at the bed. In an effort to reveal short time- and length-scale variability, measurements were made at a time interval of hours and over a length scale of 10–15 m. All data were collected during the same month (June) of two consecutive years, although data from the two years were markedly different in character. We hypothesize that this is due to variation in the timing of seasonal transitions: one year’s data represent the late-winter mode of the drainage system, while data from the other year represent the transition from winter to spring.

The field research was conducted on Worthington Glacier, Chugach Mountains, Alaska, U.S.A. Worthington Glacier is a temperate valley glacier, about 8 km long, 1 km wide and 200–220 m thick near the equilibrium line. The measurements were made just down-glacier of the equilibrium line (Fig. 1) in a reach of the glacier that has been mapped in detail with ice-penetrating radar (Welch and others, 1998). This reach has also been the focus of several detailed investigations of stress–strain relationships and glacier motion (e.g. Harper and others, 1998; Pfeffer and others, 2000).

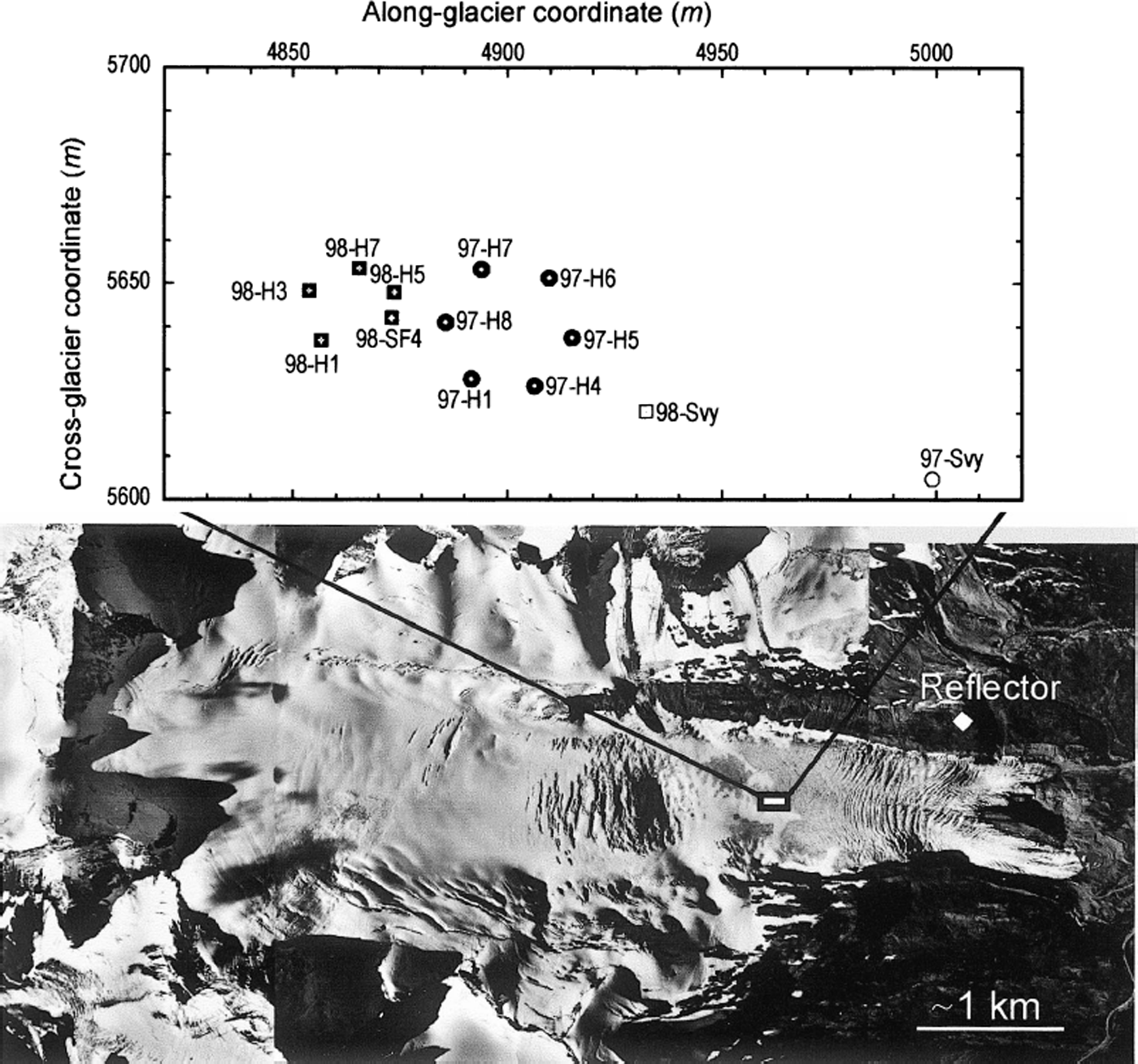
Fig. 1. Vertical air photograph of Worthington Glacier showing the location of the borehole and velocity measurements. Flow direction is from left to right. Holes drilled in 1997 are shown as squares; holes drilled in 1998 are shown as open circles. The survey sites in 1997 (97-Svy) and 1998 (98-Svy) are shown.

2. Data Collection

2.1. Surface measurements

Seasonal velocity

Surface velocities were measured within the study reach between 1992 and 1998. During most of these years, 20–60 velocity markers were surveyed daily to weekly between June and August, and 4–12 markers were used to measure the displacement over the period September–May. The survey methods, data reduction and error analysis are described in Harper and others (1996).

Short-term velocity

High-resolution surface velocity data were collected at one point on the glacier surface using a laser ranging system. The laser ranger was installed on the glacier, and retro prisms were mounted on the valley wall, approximately 1.125 km from the ranger (Fig. 1). The laser ranger was fixed to the glacier surface via three footings that were drilled through the seasonal snow and into glacier ice.

Glacier displacement was measured as the laser ranger moved toward the prism array. Displacements were measured four times daily as weather permitted. The measurements were not always made at equal time intervals but were made within a 30 min window. Each measurement consisted of the mean and standard deviation of several hundred distance recordings made by the laser ranger over approximately 10 s. An error component of velocity was then computed from the standard deviation of these measurements.

The distance measured by the laser ranger was not directly in line with the direction of maximum surface movement. To correct for this, the laser ranger itself was surveyed from the valley wall every 2–3 days. The flow path of the laser ranger was then used to correct the measured displacements in order to compute the high-time resolution velocity vector.

2.2. Borehole measurements

Boreholes extending approximately 200 m to the bed of the glacier were drilled using hot-water methods. The diameter of the holes was approximately 0.1 m. In 1997, six boreholes spaced 15 m apart were drilled for the study, and five holes with a similar spacing were installed in 1998 (Fig. 1). The bed was identified during drilling when the measured load on the drill stem fell to zero as the stem came to rest on the glacier bed. Connection of the holes with the basal hydrological system was confirmed by monitoring the water level in the holes during drilling: a sudden draining of the hole indicated that communication had been established with the basal system at a pressure below ice overburden pressure.

A submersible video camera was lowered down each hole immediately after drilling. The holes were inspected for connection with the basal drainage system, degree of water turbidity and basal sediment character. Each hole’s connection to the basal hydrological system was confirmed by visual inspection of the motion of air bubbles, turbidity clouds or small sediment particles. The holes were re-filmed repeatedly during the study periods, at least every other day and often more frequently. The repeat video observations suggested that during both years all of the holes remained connected to the hydrological system for the entire period of study.

We believe that none of these boreholes intersected englacial conduits. Three lines of evidence support this: (1) sudden changes in water level in the hole were not observed while drilling at depths above the bed; (2) each hole was filmed multiple times with a video camera, and no conduits were observed within the borehole walls; and (3) statistical analysis of the concentration of conduits within this reach of the glacier suggested that conduits make up only (2.0 × 10⁻²) − (9.4 × 10⁻⁴)% of the ice mass (Harper and Humphrey, 1995).

Ice deformational velocity

Englacial deformation within the study area was measured by repeated inclinometry of boreholes. Data were collected in the study reach in an array of 30 boreholes over a 90 day interval during 1994 (Harper and others, 1998), and within four boreholes over the year-long interval 1997/98. The latter boreholes were fitted with wire cable in 1997, and then redrilled in 1998 by following the wire through frozen portions of the hole. The drilling, inclinometry and data-processing techniques are presented elsewhere (Harper and others, 2001).

Sliding velocity

Sliding velocity was directly measured via time-lapse videography of the bottom of boreholes. The procedure consisted of lowering the camera to within 0.1 m of the base of the holes and fixing it in place. Video recordings of the bed were then made over various time periods, from continuous filming for up to 10 hours, to time-lapse filming at 30 min intervals for 24 hours. Sliding velocity was measured by tracking the displacement of features on the bed relative to the ice of the borehole wall.

Water levels

Each year, the water level in one hole was measured at 5 min intervals using a pressure transducer, installed at approximately 150 m depth and attached to a data logger at the surface. The water levels in the other holes were measured manually at least four times per day. The manual measurements were not made at exactly the same time of day, but within a 30 min window.

The water level in each hole was monitored as a proxy measurement of the subglacial water pressure in the region of the hole. Thus, holes were essentially used as manometers. This technique is only valid provided that: (1) the hole is well connected with the basal hydrological system; (2) surface and englacial water inputs to the hole do not influence the hydrological system or water level in the hole; and (3) the volume of the hole is small compared to the volume of water at the bed. Fluctuating water levels, as well as video observations of water flow at the bed, imply that the holes were always connected to the drainage system. As discussed previously, several lines of evidence suggest that there were no englacial conduit inputs to the boreholes. We also assume that the presence of the boreholes did not significantly alter the basal drainage system since existing holes showed no discernible changes in water level or turbidity when new holes connected to the drainage system. Nevertheless, we note that a major assumption is made hereafter by using borehole water levels to refer to the “basal water pressure”.

3. Results

3.1. Bed observations

A combination of radar measurements, the depths of more than 140 boreholes drilled for various studies, and video observations of hummocks on the bed suggest that the topographic relief of the bed within the region is on the order of a few meters up to a maximum of about 10 m. Video observations of the bed showed it to be a patchwork of bare bedrock and bedrock covered by coarse sediment with particles 10–100 mm in diameter (Fig. 2). Time-lapse recordings of holes moving over cavities and hummocky terrain, and video observations where drilling penetrated sediment cover both suggest that the sediment layer was typically 10 cm, and was not more than a few tens of cm, in thickness. Filming of adjacent holes spaced 10–15 m apart, both in this study and in previous work (e.g. Harper and Humphrey, 1995), suggests that the patches cover considerably less than 50% of the bed and the aerial extent of individual sediment patches is limited to 1–10 m. No differences in the character of the basal sediment were noticeable between the two years of observation. Therefore, we believe that the sediment cover is not of sufficient thickness and extent to allow till deformation to be a significant contributor to glacier motion.

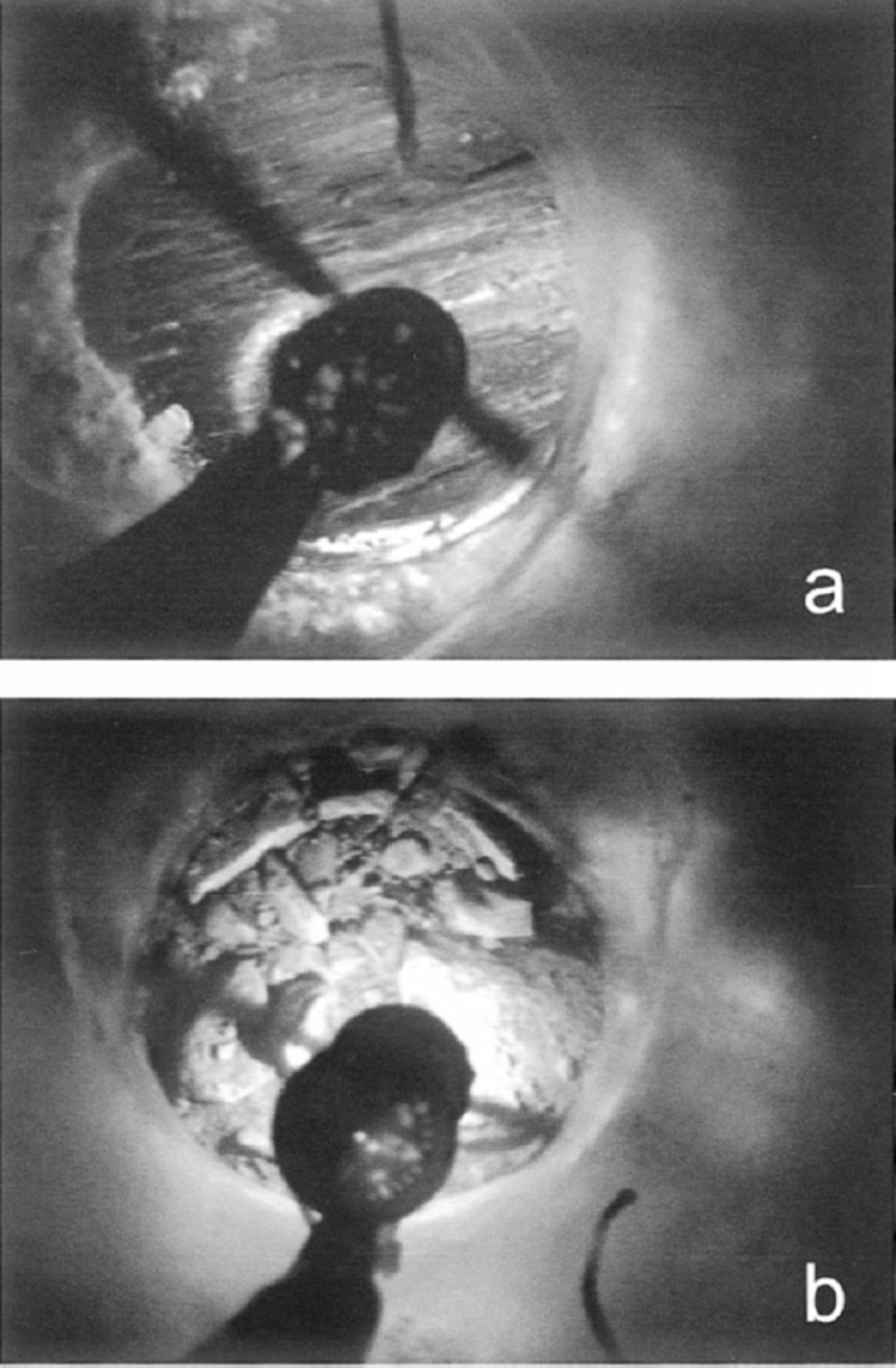
Fig. 2. Borehole video images of hole 98-H5 filmed 5 days apart in 1998. (a) The hole initially encountered bare bedrock. (b) Five days later the hole had moved over coarse sediment. The sediment remained at the base of the hole throughout the observation period and overturned as the hole moved over the bed.

3.2. Seasonal velocity variability

The survey program defined a seasonal pattern to Worthington Glacier’s surface velocity similar to those identified on numerous other glaciers (e.g. Hodge, 1974; Hooke and others, 1983). Worthington Glacier’s seasonal velocity pattern consists of a period of rapid motion during the late spring to early summer, followed by a steady decrease in speed over the remainder of the summer and fall. Average weekly velocity during the spring peak is on the order of 20–30% higher than during the late summer (Harper and others, 1996). For example, in 1994 the mean velocity of 64 stakes located near the study reach was 225 mm d⁻¹ during 2 weeks of late June, but slowed to <181 mm d⁻¹ by early August. The timing and magnitude of the spring velocity peak is not necessarily consistent from year to year and appears to be related to meteorological conditions driving water input to the glacier system (Röthlisberger and Lang, 1987). While no mid-winter surveys were conducted, measured displacements between late fall and early spring suggest that velocities remain relatively low throughout the winter.

Annual surveys may be used to infer the timing of the 1997 and 1998 measurements with respect to the seasonal velocity changes. The annual surface displacement of ice within the study reach averaged approximately 75 m in the years 1992–96, with a variability of about 10% from year to year. Stakes installed in late summer 1996 were displaced an average of 72 m by June 1997. This suggests a full seasonal cycle, including the spring speed-up, had nearly been completed between the June 1997 measurements and the previous summer. In 1998, however, the measured displacements of 1 year-old markers averaged only 54 m. This implies that the seasonal peak had not yet arrived during the 1998 study period. The earlier arrival of the spring speed-up in 1997 was likely the result of an earlier than usual melt wave due to warm, dry conditions that resulted in bare ice across the entire study reach by the end of June. Conditions in 1998 were more typical of our experiences at the site, with roughly 2 m of snow covering the study reach at the end of June.

3.3. Short-term surface velocity

The mean velocity from the 1997 record is 205 mm d⁻¹ (Fig. 3a). The time series is characterized by high-amplitude swings between fast and slow events. Some sustained periods of velocity in excess of 250 mm d⁻¹ were observed, while slow periods with movement at rates of 120–150 mm d⁻¹ were also present. Thus, the measured peak velocities were about twice the minimum values.

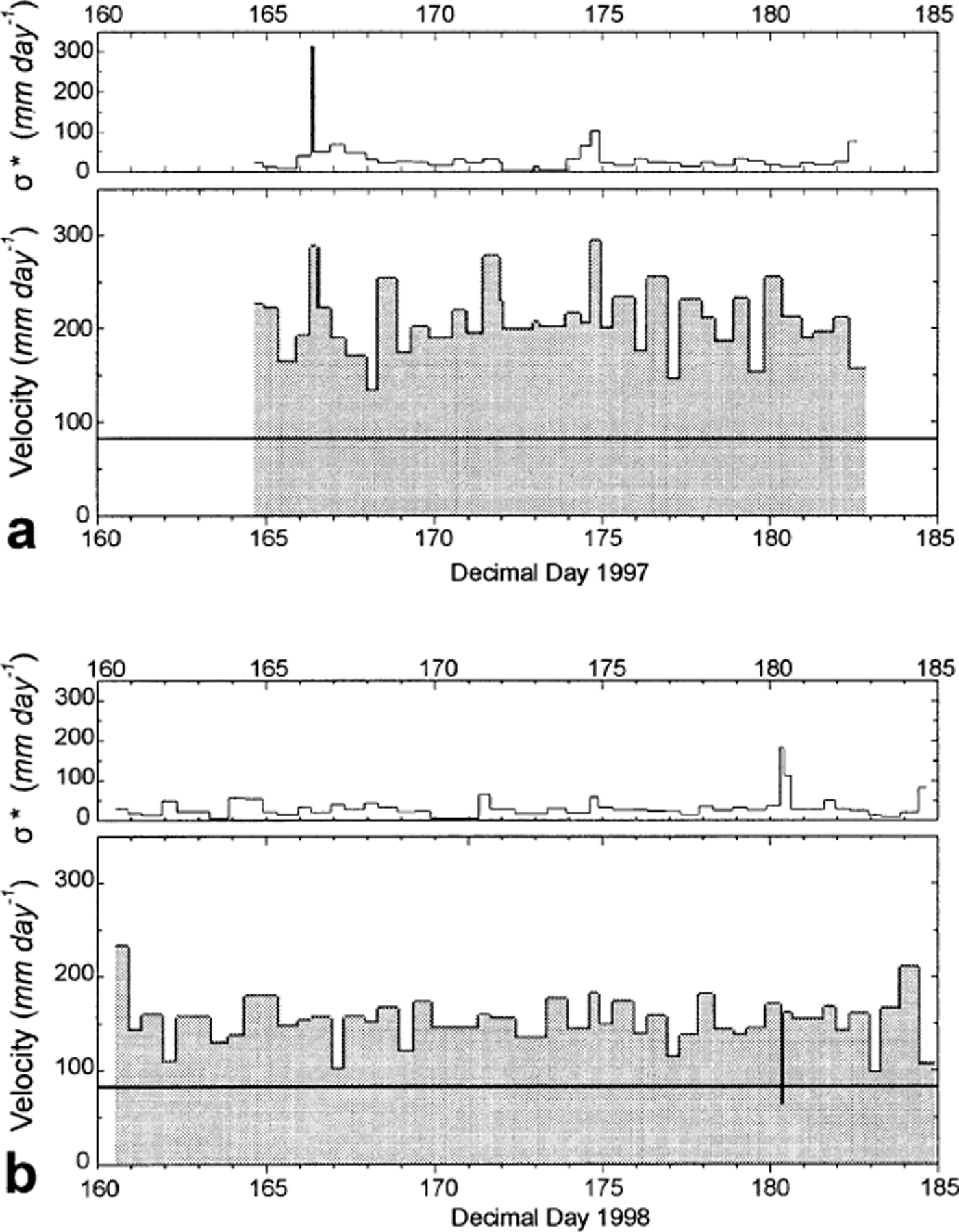
Fig. 3. Time series of surface velocity during 1997 (a) and 1998 (b). In each pair, lower panel shows velocity and upper panel shows the possible error component (σ ^*). Error is calculated as , where σ ₁ and σ ₂ are the standard deviations of the first and second distance measurements and t is the time interval between measurements. The error velocity is considered a worst case, as the errors are not necessarily additive. Measured deformational velocity of hole 97-H6 during 1997/98 (83 mm d⁻¹) is shown by solid horizontal line in each velocity panel. Low-velocity spike at day 180.3 is believed to be a survey error.

Velocities during the 1998 study interval averaged about 25–30% less than those measured in 1997, with a mean velocity of only 150 mm d⁻¹ (Fig. 3b). Compared to the 1997 time series, motion during 1998 was relatively steady with small-amplitude velocity swings. Several sustained periods with low velocity (e.g. 100–120 mm d⁻¹) were also observed. The peak velocities were also lower than in 1997, typically on the order of only 180 mm d⁻¹.

3.4. Ice deformational velocity

Borehole inclinometry measurements revealed spatial gradients in the flow field but no evidence for time-dependent deformation (Harper and others, 1998). The profile of borehole 97-H6 following 374 days of deformation is shown in Figure 4. The hole, which was approximately straight and vertical immediately after drilling (Harper and others, 2001) , has an offset between its top and bottom of about 30 m due to internal ice deformation. The total velocity of the top of the borehole that may be attributed to internal deformation is 83 mm d⁻¹. The other three boreholes showed very similar profiles.

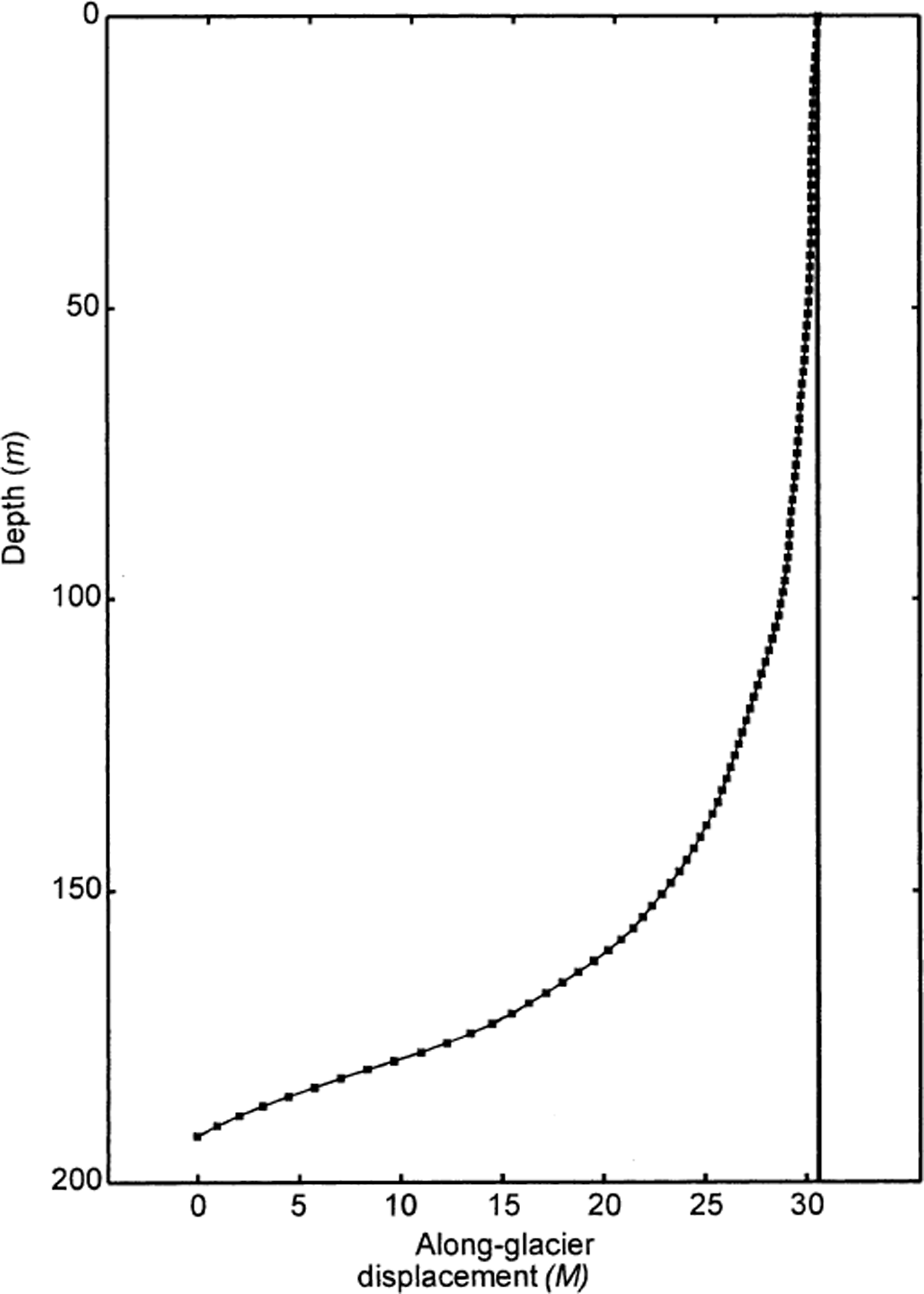
Fig. 4. Trajectory of borehole 97-H6 after 1 year of deformation. Abscissa gives the displacement of points along the hole relative to the bottom of the borehole. The hole was drilled to the bed and measured to within 1 m of the bed.

3.5. Sliding velocity

A time series of the displacement of a point on the bed relative to the borehole wall is shown in Figure 5. These data were collected over a 2 hour interval (1930–2130 h) on decimal day 171, 1997. Displacements were calculated at 5 min intervals, with an estimated measurement error of < 1 mm. A least-squares fit to the displacement record gives a mean sliding velocity of 128 mm d⁻¹. Slight variations in the sliding rate were observed, although these were relatively minor with no major stick-slip events evident. Other time-lapse recordings made during both 1997 and 1998 also contained no evidence of stick–slip motion.

Fig. 5. Sliding velocity from time-lapse video and effective pressure in borehole 97-H5. (a) Displacement time series of a point on the bed relative to the ice within the borehole wall. Measurements were made from 1930 to 2130 h on the evening of day 171 in 1997. (b) Effective pressure (overburden minus water pressure) during the same period.

Seven surface velocity measurements were made during the interval shown in Figure 5. The mean surface velocity during the interval was 199 mm d^−l, and steadily decreased during the sliding-velocity measurement from a recent peak of 300 mm d⁻¹. Over the 2 hour interval, the mean sliding velocity and the deformational velocity sum to 211 mm d⁻¹, or to within about 5% of the measured surface velocity. While the consistency of the three velocity components is reassuring, we note that the surface velocity measurements have high error since they represent small displacements collected over short time intervals.

3.6. Water levels

The 1997 time series of water levels are displayed in Figure 6. During the entire record, none of the holes showed cyclic variations on a diurnal, or any other, time-scale. Each of the holes did exhibit fluctuations in pressure over a wide range of values, from greater than overburden pressure to less than half of overburden.

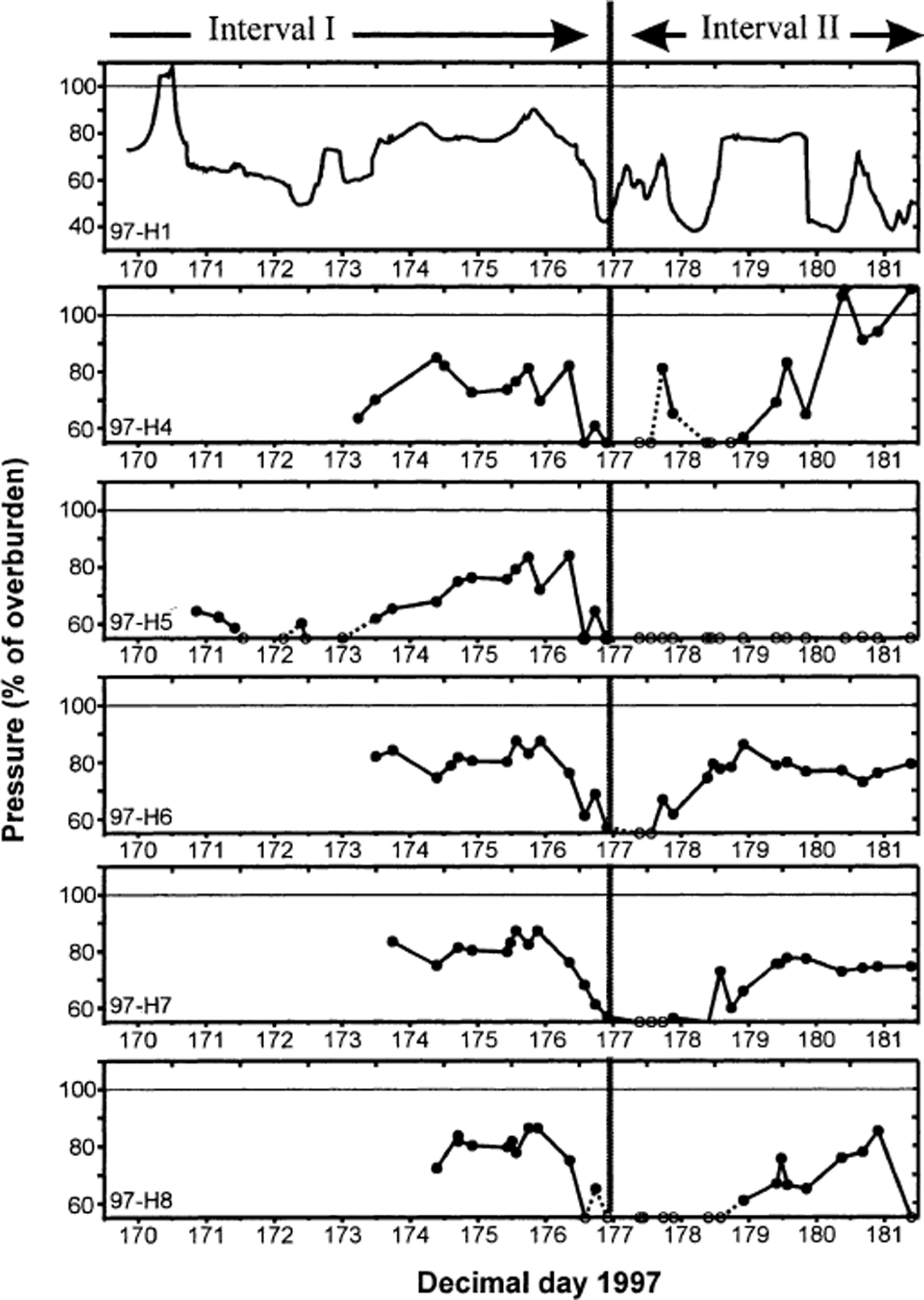
Fig. 6. Time series of borehole water levels during 1997 displayed as a percentage of overburden pressure. Interval I had roughly synchronous water levels. Interval II had complete asynchroneity between holes. Open circles represent water levels known only as having been less than 55% of the ice overburden pressure; dashed lines have uncertain slopes.

The time series is divided into time intervals I and II (Fig. 6) during which the fluctuations of borehole water levels were different. During interval I, each of the boreholes exhibited roughly similar pressure fluctuations over time intervals of hours to days. In two instances, pairs of holes temporarily showed variations in water level that were different from those in the other holes. In each case the pairings involved different holes.

Interval II is characterized by water-level variations that differed from hole to hole. The period began with universally low water pressure, followed by asynchronous changes over the remainder of the record. For example, 97-H5 showed pressure of less than 55% of overburden for the remainder of the period; hole 97-H7 showed only minor variability, in the vicinity of 80% of overburden; and hole 97-H4 showed several high- and low-pressure events, including a period of artesian flow. Pressure gradients between the holes were large, reaching values as high as 48 kPa m⁻¹ between holes 97-H4 and 97-H5 on day 180. Each hole showed at least one pressure spike during the period. However, the timing, duration and magnitudes of spikes were inconsistent between holes.

The pressure time series of the five boreholes measured in 1998 is markedly different in character than the 1997 measurements (Fig. 7). Throughout the 1998 study period, water pressures remained continuously in the range of 70–90% of overburden. The entire array of holes exhibited variations in water level that were synchronous and similar in magnitude. Water levels fluctuated diurnally, with other superimposed variations that were minor. The maximum magnitude of the diurnal swings was approximately 16% of the overburden pressure.

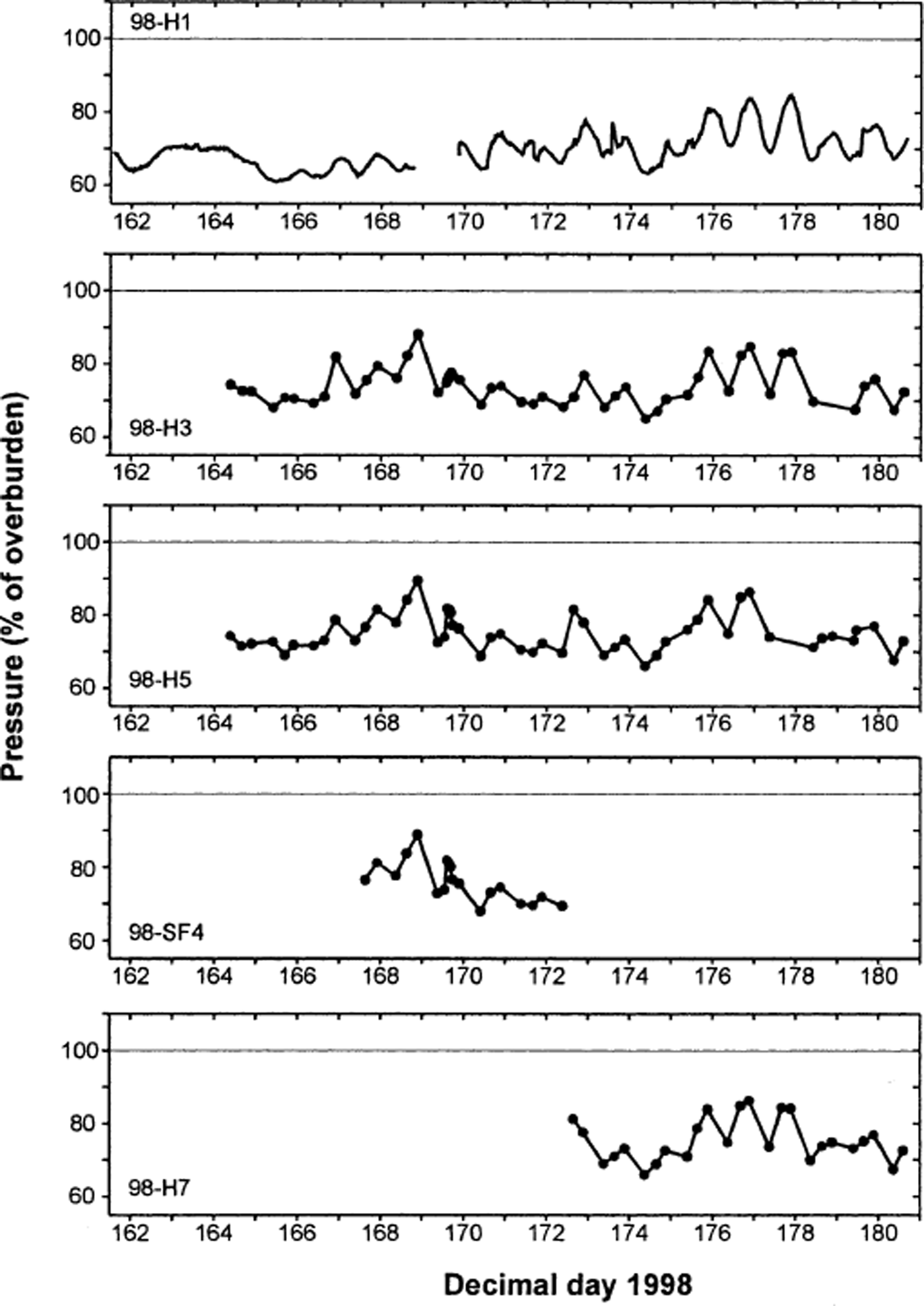
Fig. 7. Time series of borehole water levels during 1998 displayed as a percentage of overburden pressure.

4. Statistical Analysis

We use several statistical methods to examine the character of the water level and velocity time series. Our statistical objectives are not comprehensive; we simply evaluate the time series for trends and periodic patterns (i.e. diurnal variations) by testing for a difference in velocities by time of day, and by using Fourier analysis and state–space modeling techniques. Secondly, we use cross-correlations to investigate the relationship between pressure and velocity.

We begin by examining the mean velocities at different times of the day to test for evidence of time-dependent motion. The mean velocities of four equal time intervals are shown in Table 1. The evening hours in 1997 show a notably larger mean velocity than other times of day, whereas in 1998 they show only a slightly higher mean velocity than other time intervals. The means are formally compared by testing for equality of the four means. However, there are significant correlations between the different times of the day, which must be accounted for to appropriately test for a difference in the means. The statistic described by Jobson (1992, p. 160), which has an F distribution and yields a p value, is used to perform a test in the presence of these correlated observations. The p value gives a statistical measure of the difference between means of a group, with smaller p values indicating more difference between the means. The p value for the 1997 velocities indicates that the various time intervals are significantly different from one another, while the 1998 p value suggests a smaller difference between mean velocities of different time periods of the day (Table 1). Thus, there is stronger evidence for time-variable motion in 1997 than there is in 1998.

Table 1. Mean surface velocities (mm d⁻¹) over hourly time intervals

State–space models are used to linearly decompose a series into trend, systematic and irregular components. The trend component describes long-term changes in the mean of the series, the systematic component represents repeating patterns, and the irregular component models other, short-term structures in the series (Shumway and Stoffer, 2000). The observed series and independent components are assumed to have errors that follow independent normal (Gaussian) distributions that do not change over time. Our original observations of water level and velocity were first linearly interpolated to provide observations on an evenly spaced time grid with four observations per day. State–space models were then fit to each series using the Kalman filter and Expectation-Maximization (EM) algorithm, where the Kalman filter linearly filtered the series into these different components and the EM algorithm was used to estimate model parameters (Shumway and Stoffer, 2000).

Once the state–space model was fitted, the trend was subtracted from the original series. Removal of the trend allows Fourier analysis to focus exclusively on short-term periodic variations in the series, including possible diurnal patterns. The power spectrum at differing frequency oscillations was then computed using a discrete Fourier transform. The periodogram for each “de-trended” series is displayed in Figure 8. These periodograms differ only slightly from those calculated directly from raw data. The periodograms of 1997 velocity and 1998 pressure display peaks of relatively high power at 1 cycle per day. In contrast, the 1997 pressure and 1998 velocity show no major peaks at any cycle of up to 2 days. Fourier analysis relies on large-sample theory. Thus the results should be used only as an indication of the strength of the diurnal pattern and absence of variation at other frequencies.

Fig. 8. Periodograms showing the power spectrum of the pressure and velocity time series during 1997 (spring) and 1998 (late-winter) study intervals.

State–space modeling offers an independent check on the Fourier periodograms through comparison of models that include or do not include a diurnal component. Additionally, state–space models do not rely on the large-sample assumptions of the Fourier analysis. Model fits were evaluated using Akaike’s information theoretic criterion (AIC) as described in Kitagawa and Gersch (1996). The AIC comparison favors models with a diurnal component for the 1997 velocity and 1998 pressure series. Agreement of the hypothesis-testing, Fourier and state–space methods adds confidence to the conclusions regarding the presence or absence of diurnal variations.

Finally, lagged and unlagged Pearson correlation coefficients were calculated between the pressure and velocity records for a range of ±1 day. No statistically significant cross-correlations between velocity and pressure were identified. This suggests that there is no significant linear relationship between pressure and velocity. The possibility remains, however, that the cross-correlations did not identify a relationship because the sampling was insufficient, or because the relationship is non-linear and more complicated.

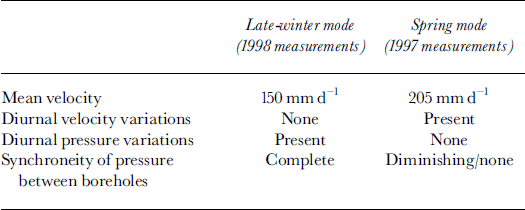
From the statistical analysis of pressure and velocity data we draw the following conclusions: (1) a strong diurnal cycle is present in both the 1997 velocity and 1998 pressure series; (2) no significant diurnal cycle exists within the 1997 pressure and 1998 velocity series; (3) there is no simple correlation between water pressure and velocity. These results are summarized in Table 2.

Table 2. Characteristics of water-pressure and velocity time series

5. Discussion

5.1. Evolution of drainage system

Datasets were collected during the months of June 1997 and June 1998. We assume, based on observations of surface melt and annual displacements, that 1998 and 1997 data represent late-winter and early-spring hydrological conditions, respectively (see section 3.2). During late winter (1998 data) the water pressure at the bed underwent diurnal fluctuations and showed complete spatial synchroneity at the 15 m length scale. Thus, all sampled points on the bed were in good communication with each other, and at least some points on the bed were well connected to the surface. The basal hydrological system is inferred to have had a relatively low volume due to the general lack of available water at this time of the year; drainage in the borehole area likely occurred through a system of linked cavities. Water flux through the system was sufficiently small that daily increases in input caused a pressure build-up over the bed, but were low enough that the pressure fully recovered on a diurnal cycle.

Later in the hydrological year, during the spring velocity peak (1997 data), meltwater production at the surface was relatively high, with strong diurnal variations. Initially, regions of the bed with similar water pressure encompassed several holes, indicating that interconnected regions extended over tens of meters. Eventually there was no common pattern in the pressure of holes that were 15 m apart. We surmise that interconnected areas of the bed had decreased in size to less than the hole spacing. At no time did the pressure vary diurnally in response to input variations. We hypothesize that during this transitional period the initial drainage configuration of linked cavities was evolving into a new drainage system. The low-pressure areas may have been connected to a fast draining system while the adjacent high-pressure areas were hydraulically isolated. If a conduit system was in fact evolving, the process was episodic as holes tended to connect and disconnect to the low pressure. This process could be related to high sliding rates, which may cause sudden re-routing of the drainage over the hard bed.

Worthington Glacier’s apparent breakdown of spatially synchronous and diurnally varying water pressure is the reverse of observations of Haut Glacier d’Arolla, Switzerland, where these hydraulic characteristics were established over time (Gordon and others, 1998). The Arolla data were collected in summer, from late July to late August, when a major subglacial channel is interpreted to have been established. Assuming that the hydrological processes between the two glaciers are similar, a possible interpretation would be that our data represent the transition from a winter mode with low sliding velocity (linked cavities) to a spring mode with high sliding velocity (hydraulically isolated patches with areas of fast drainage), while the Gordon and others (1998) data represent a later transition from the spring mode to a summer mode.

5.2. Relationship between velocity and pressure

The study reach showed sliding variability that at no time matched local pressure fluctuations: when diurnal pressure variations were present, there were no corresponding variations in motion, whereas daily sliding variations occurred with no corresponding pressure signal. This suggests that local water pressure was not the primary factor driving the sliding velocity of the reach.

The relevant pressure, however, may be associated with a longer length scale than the 15 m spacing of the boreholes. Kamb and others (1994) suggest that sliding velocity is controlled by the mean coupling length over which basal shear stress is effectively averaged by ice dynamics. The longitudinal coupling length for Worthington Glacier, using Kamb and Echelmeyer’s (1986) analysis, is on the order of 200–600 m. The local water pressure may differ from the 200–600 m mean due to local differences in the drainage system. A difficulty with this explanation is that it requires a period when local pressure varied diurnally while the regional mean did not, and another period when the regional mean varied diurnally while local pressure did not.

Another possible explanation for the lack of correlation between local pressure/velocity cycles is that the local velocity resulted from longitudinal forcing by the ice. If the glacier below the study reach was experiencing enhanced sliding rates, the result could be pulling on the study reach from below. A diurnal cycle in the pulling could explain diurnal motion of the study reach at times when the reach’s pressure was non-cyclic. Differential sliding rates between the study reach and the lower glacier could result from focused water input to the bed at the lower icefall, differences in the subglacial drainage systems of the two locations, or a time lag in meltwater generation and routing to the bed along the length of the glacier (Fountain and Walder, 1998).

A final explanation for the lack of correlation between pressure and velocity could be that water storage at the bed is the primary factor in determining the sliding speed. Forcebalance modeling of basal processes suggests that sliding speed directly correlates with storage but storage does not necessarily correlate with pressure (Humphrey, 1987). Consequently, sliding speed may not necessarily correlate with pressure. Unfortunately, we do not have measurements of basal water storage and can only offer qualitative field observations suggesting the magnitude and cycles of sliding speed were similar to the magnitude and cycles of water input.

6. Summary and Conclusions

The character of Worthington Glacier’s motion and subglacial hydrological conditions showed significant change between a late-winter mode and a spring mode. In late winter the glacier’s surface velocity was relatively small and steady, averaging 150 mm d⁻¹. During a few brief intervals, the glacier moved almost entirely by ice deformation. In late winter, the basal water pressure measured in boreholes spaced 15 m apart was characterized by synchronous diurnal variations without spatial pressure gradients.

In contrast, during the spring velocity peak the surface velocity fluctuated diurnally, averaged 205 mm d⁻¹, and had peak periods in excess of 250 mm d⁻¹. Comparisons of surface velocity with measurements of internal deformation indicate that sliding dominated the motion. Water pressures during this time fluctuated widely but did not exhibit cyclic behavior. Each borehole showed unique changes in water level, with strong spatial pressure gradients between holes spaced only 15 m apart. We hypothesize that the changes in the pressure field from late winter to spring represent the breakdown of a linked-cavity system.

Analysis of the data collected on Worthington Glacier identified no simple relationship between water pressure and sliding speed, in terms of either magnitudes or temporal cycles. Diurnal variations in sliding speed occurred when there were no diurnal water-pressure fluctuations, while diurnal water-pressure variations were observed when sliding was non-periodic.