1. Introduction
Owing to limitations of time and expense, field measurements of variables such as mass balance and velocity have been made on only about 250 out of the roughly 160 000 glaciers worldwide. Some glacier properties are relatively easy to measure (such as surface areas from remote sensing), but others are virtually impossible to measure without major investments in ground-based field studies (e.g. ice volume, thickness, flux and mass balance). As a substitute for direct measurements, power-law- scaling relations are gaining in popularity as a simple method for relating unknown glacier quantities to easily measured parameters such as length and surface area. Volume–area relations are a much-studied example (e.g. Reference Macheret, Cherkasov and BobrovaMacheret and others, 1988: Reference Chen and OhmuraChen and Ohmura, 1990; Reference Meier and BahrMeier and Bahr, 1996). Response-time–area relations are another example (Reference Pfeffer, Sassolas, Bahr and MeierPfeffer and others, 1998). When no direct observations are available, these power laws can also be used to predict the probability that a glacier has some particular volume, response time, average velocity or other properly (Reference BahrBahr, 1997a).
These predictions and power-law relations, however, all rely on a set of three closure conditions (analogous to boundary conditions) which fix the power-law scaling exponents (Reference BahrBahr and others, 1997). These closures are the relations between glacier lengths and (1) widths, (2) slopes and (3) mass-balance rates. Observations have shown that valley glacier width is related to length raised to an exponent of approximately 0.6 (Reference BahrBahr, 1997b). In addition, indirect theoretical considerations suggest that valley-glacier slopes may the independent of length (Reference BahrBahr and others, 1997), but this has not been verified by direct observations.
In this paper, we use recently compiled mass-balance data (Reference Dyurgerov and BahrDyurgerov and Bahr, 1999) to examine the third closure condition and to determine if glacier length scales with a characteristic measure of the mass-balance rate. The mass-balance rate ![]() can be measured at every point on a glacier; scaling relations use the balance rate from a single representative point or average of points. Although it is an obvious first choice, averages over an entire glacier are not useful, because no matter how large or small their size, glaciers in a steady state must have net balances near zero. Instead, a commonly selected characteristic point measurement is the balance rate at the terminus or the average along the terminus (e.g. Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others, 1989; Reference OerlemansOerlemans, 1997; Reference Pfeffer, Sassolas, Bahr and MeierPfeffer and others, 1998). The characteristic value could be selected elsewhere, such as at the head of a glacier, but in this paper we continue with the convention of choosing the balance rate at the terminus,
can be measured at every point on a glacier; scaling relations use the balance rate from a single representative point or average of points. Although it is an obvious first choice, averages over an entire glacier are not useful, because no matter how large or small their size, glaciers in a steady state must have net balances near zero. Instead, a commonly selected characteristic point measurement is the balance rate at the terminus or the average along the terminus (e.g. Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others, 1989; Reference OerlemansOerlemans, 1997; Reference Pfeffer, Sassolas, Bahr and MeierPfeffer and others, 1998). The characteristic value could be selected elsewhere, such as at the head of a glacier, but in this paper we continue with the convention of choosing the balance rate at the terminus, ![]() . Characteristic quantities are enclosed in square brackets to clearly distinguish them from functions which can have different values at different points. For example
. Characteristic quantities are enclosed in square brackets to clearly distinguish them from functions which can have different values at different points. For example ![]() is a function of position, while [
is a function of position, while [![]() ] is selected to be the value at the terminus,
] is selected to be the value at the terminus, ![]() .
.
Individual glaciers are expected to have increasingly negative mass-balance rates at the terminus as they grow larger and longer and sample the climate at lower elevations. Given a collection of glaciers, however, it is less clear if the larger glaciers will typically have more negative balance rates at the terminus than the smaller glaciers in the same collection. Certainly local climate may play a role. A large continental glacier could have a less negative terminus balance rate than a similar-sized maritime glacier. In addition, debris on the terminus, measurement errors and other considerations specific to each individual glacier will add significant noise to any scaling relation between glacier size and terminus mass-balance rate. However, previous observations of accumulation area ratios (the ratio of accumulation area to glacier area) and volume–area relations have already suggested indirectly that [![]() ] may scale roughly as the square of glacier length (Reference BahrBahr, 1997b; Reference BahrBahr and others, 1997). If such a relation (or similar one) can be confirmed, even partially and despite the noise, then the balance-rate closure condition could be used more confidently in a variety of scaling applications ranging from climate-change studies that use response-time estimates (Reference Pfeffer, Sassolas, Bahr and MeierPfeffer and others, 1998) to sea-level-rise calculations which use glacier volumes (Reference BahrBahr and others, 1997).
] may scale roughly as the square of glacier length (Reference BahrBahr, 1997b; Reference BahrBahr and others, 1997). If such a relation (or similar one) can be confirmed, even partially and despite the noise, then the balance-rate closure condition could be used more confidently in a variety of scaling applications ranging from climate-change studies that use response-time estimates (Reference Pfeffer, Sassolas, Bahr and MeierPfeffer and others, 1998) to sea-level-rise calculations which use glacier volumes (Reference BahrBahr and others, 1997).
Using mass-balance observations for 68 valley and cirque glaciers, we regress glacier length [x] against terminus balance rate, and vice versa; these show a definite scaling trend that suggests ![]() with m constrained to be within the approximate range 0.64–1.7. As expected, the data are noisy and the regressions have relatively low correlations. Nonetheless, the data do imply that terminus balance rates for all glaciers follow roughly the same power-law scaling trend with length.
with m constrained to be within the approximate range 0.64–1.7. As expected, the data are noisy and the regressions have relatively low correlations. Nonetheless, the data do imply that terminus balance rates for all glaciers follow roughly the same power-law scaling trend with length.
2. Observations
Reference Dyurgerov and BahrDyurgerov and Bahr (1999) describe a compilation of 80 glaciers and ice caps worldwide, each with a comprehensive set of morphological and mass-balance observations. We consider a subset of these glaciers which is restricted to cirque and valley glaciers. Polar ice caps were excluded because of potential differences from temperate ice dynamics, as were calving glaciers because the terminus mass balances are complicated by calving events. Two additional glaciers (Sonnblickkees, Austria, and Nordlicher Schneeferner, Germany) were also eliminated because their terminus mass balances were positive over the periods of observation (1964–78 and 1967–68, respectively), suggesting unusual local climatic conditions or significant departures from steady-state conditions.
For the remaining 68 glaciers, we have measurements of terminus mass-balance rate, length and surface area. As discussed, the characteristic mass-balance rate is measured at the terminus, so ![]() is the same as
is the same as ![]() . The glacier length, x, and area S are also the same as the characteristic length [x] and characteristic area [S]. Because it does not make a difference in the context of this paper, we will use the characteristic quantities ([x], [S] and [b]) interchangeably with the measured values of the actual variables x, S and b
t on each glacier. Reference Hutter and ReidelHutter (1983), Reference Jóhannesson, Raymond and WaddingtonJóhannesson and other (1989), Reference FowlerFowler (1992) and many others describe the choice of characteristic quantities in more detail.
. The glacier length, x, and area S are also the same as the characteristic length [x] and characteristic area [S]. Because it does not make a difference in the context of this paper, we will use the characteristic quantities ([x], [S] and [b]) interchangeably with the measured values of the actual variables x, S and b
t on each glacier. Reference Hutter and ReidelHutter (1983), Reference Jóhannesson, Raymond and WaddingtonJóhannesson and other (1989), Reference FowlerFowler (1992) and many others describe the choice of characteristic quantities in more detail.
3. Analysis
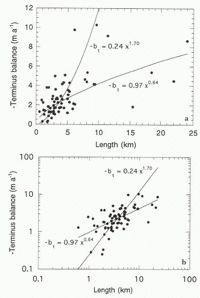
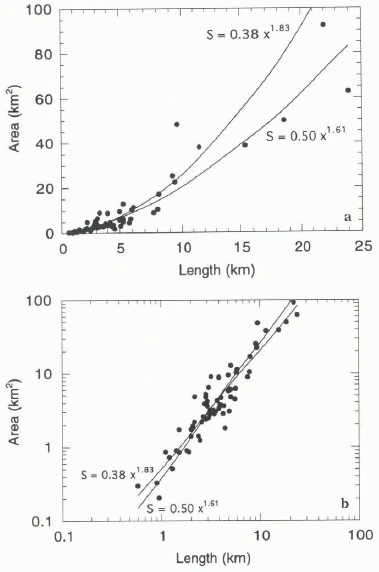
For the 68 valley and cirque glaciers, the terminus balance rate can be plotted against glacier length (Fig. 1) and size (Fig. 2). Surface area and length are also compared (Fig. 3). The terminus balance-rate data have a lot of scatter, but there is a clear trend towards increasing size and length with increasingly negative terminus mass-balance rates.
Correlation coefficients, r, for each plot suggest that power-law relations are as likely as linear relations. For area vs length, power-law fits give r = 0.94, and linear fits give r = 0.93. For terminus balance rate vs length, r = 0.61 for power-law fits, and r = 0.60 for linear fits. For terminus balance rate vs area, r = 0.56 for power-law fits, and r = 0.57 for linear fits. Power-law relations between these characteristic quantities are expected based on dimensional arguments. Visual inspections of Figures 1–3 suggest that the power-law relations are reasonable. (Because area and length have a clear power-law relation, the balance–length relation is a power law if, and only if, the balance–area relation is a power law. In other words, showing one will be equivalent to showing the other. Consequently, much of this discussion will focus on establishing the balance–length relation.)

Fig. 1. Terminus balance rate vs glacier length with OLS regressions ![]() and
and ![]() . (The two equations are obtained by using
. (The two equations are obtained by using ![]() as the dependent and independent variable, respectively.) (a) Linear plot. (b) Log–log plot.
as the dependent and independent variable, respectively.) (a) Linear plot. (b) Log–log plot.
Three different regressions, two ordinary least-squares (OLS) and one organic correlation (OC), were performed for each pair of variables (![]() vs x,
vs x, ![]() vs S, and x vs S). OLS regressions assume that one variable is dependent on the other (e.g.
vs S, and x vs S). OLS regressions assume that one variable is dependent on the other (e.g. ![]() (x)), and then minimize the variance of only the dependent variable relative to the fit. For example, using OLS we can calculate two linear regressions,
(x)), and then minimize the variance of only the dependent variable relative to the fit. For example, using OLS we can calculate two linear regressions, ![]() and
and ![]() . The slopes are given by
. The slopes are given by ![]() and
and ![]() where s
i
is the standard deviation of i. If the two OLS regressions were the same, then b
1 would equal 1/b
2, which is not the case (unless the relation between the two variables were perfect). OLS regressions are most appropriate when one variable can be identified as independent and the other as dependent. On the other hand, OC regressions minimize the variance of both variables simultaneously, so OC is a more appropriate choice when neither variable is clearly dependent on the other (e.g. Reference TillTill, 1974). For OC regressions, the slopes are given by
where s
i
is the standard deviation of i. If the two OLS regressions were the same, then b
1 would equal 1/b
2, which is not the case (unless the relation between the two variables were perfect). OLS regressions are most appropriate when one variable can be identified as independent and the other as dependent. On the other hand, OC regressions minimize the variance of both variables simultaneously, so OC is a more appropriate choice when neither variable is clearly dependent on the other (e.g. Reference TillTill, 1974). For OC regressions, the slopes are given by ![]() and
and ![]() , so b
1 = l/b
2 as expected.
, so b
1 = l/b
2 as expected.
Table 1 lists the scaling exponents determined by each of the different regressions. The appropriate regression depends on the variable’s functional relations. Which of ![]() and [x] is dependent on the other is difficult to establish with certainty. The usual form of the continuity equation (Reference PatersonPaterson, 1994) relates ice thickness (and hence size) to mass-balance rate which implies that a glacier’s length and area are at least partially dependent on the balance flux. This suggests the OLS fits (using
and [x] is dependent on the other is difficult to establish with certainty. The usual form of the continuity equation (Reference PatersonPaterson, 1994) relates ice thickness (and hence size) to mass-balance rate which implies that a glacier’s length and area are at least partially dependent on the balance flux. This suggests the OLS fits (using ![]() as independent)
as independent)
and
are most appropriate. The functional relation between surface area and length is less clear, but previous work by Bahr (1997b) with a larger dataset (303 Eurasian glaciers) has shown that [S] ? [x] q+1 with q ≈ 0.6, so the appropriate regression is most likely to be the one that predicts an exponent of roughly 1.6. If area is selected to be dependent on length, then an OLS fit of the 68 glaciers predicts
in close agreement with the previous study. The OC regression [S] ? [x]1.71 is also reasonable.

Fig. 2. Terminus balance raie vs glacier surface area with OLS regressions ![]() and
and ![]() . (a) Linear plot. (b) Log–log plot.
. (a) Linear plot. (b) Log–log plot.
4. Discussion
Some noise in the data (and hence some difficulty in choosing an appropriate regression) is expected. Glaciers can experience similar climates, be at the same mean elevation and have the same length, but due to bedrock geometries they may have different surface slopes. Steeper glaciers of the same length will reach lower elevations and have more negative terminus mass-balance rates. Even though two glaciers may have the same length, differences in local climate can also lead to different term inns balance rates. Differences in debris cover can also alter the terminus balance rates for otherwise similar glaciers. Additional data may improve the regressions, but Figures 1 and 2 demonstrate that despite natural variability and inherent noise, a trend (holding across many glaciers) does exist between characteristic mass-balance rate and length.

Fig. 3. Glacier surface area vs length with OLS regressions S = 0.50x1.61 and S = 0.38x1.83. (a) Linear plot. (b) Log–log plot.
Establishing the existence of a scaling trend is sufficient to validate using a closure condition for mass balance, but pinning down an exact value for m is still important. The regressions suggest that the exponent m should fall roughly between 0.64 and 1.7, the latter value being optimal if the glacier length is dependent on the balance rate. Certainly, mass-balance rates are usually treated as the forcing function when studying changes in glacier geometry (e.g. Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others, 1989; Reference PatersonPaterson, 1994; Reference Raper, Briffa and WigleyRaper and others, 1996; Reference OerlemansOerlemans, 1997). So as long as climate (and not the glacier) dictates the mass-balance–altitude relation and as long as the glacier’s bedrock profile is fixed, then the glacier’s length will depend on the balance, and Equation (1) with m = 1.7 is the best option. Other arguments, however, support m = 0.64, or at least suggest that none of the values between 0.64 and 1.7 are better than another.
Table 1. Scaling exponents for OLS and OC regressions*

For example, smaller values of m appear more reasonable when considering the change in terminus balance rates with a corresponding change in length. If m = 2, then two glaciers with lengths differing by a factor of 100 (say 1 km and 100 km) will have terminus balance rates differing by a factor of 104. On the other hand, when m = 0.5, glacier lengths differing by a factor of 100 will translate to terminus balance rates differing by a factor of 10. The latter seems physically more plausible. The existing data in Figures 1 and 2 can support cither claim, but the balance and length data only span two orders of magnitude.
Both OLS regressions are shown in Figures 1–3. On the log-log plots, the fits ![]() and
and ![]() (see Table 1) appear visually to be slightly better than the regressions selected for Equations (1) and (2). Noise in the data, however, makes such visual judgements tricky, and the correlation coefficients are the same for both of the fits shown on each plot; without additional information there is no statistical reason to believe that either OLS fit is superior. These alternative OLS fits are also heavily biased by the four largest glaciers, those greater than 15 km in length (Andrei, Tiedemann and White Glaciers in Canada, and Tunsbergdalsbreen in Norway), and the fits in Equations (1) and (2) appear more reasonable if these glaciers are neglected (although we have no reason to eliminate these data points).
(see Table 1) appear visually to be slightly better than the regressions selected for Equations (1) and (2). Noise in the data, however, makes such visual judgements tricky, and the correlation coefficients are the same for both of the fits shown on each plot; without additional information there is no statistical reason to believe that either OLS fit is superior. These alternative OLS fits are also heavily biased by the four largest glaciers, those greater than 15 km in length (Andrei, Tiedemann and White Glaciers in Canada, and Tunsbergdalsbreen in Norway), and the fits in Equations (1) and (2) appear more reasonable if these glaciers are neglected (although we have no reason to eliminate these data points).
Also note that each of the OLS and OC regressions is consistent with observations of volume–area scaling. Ice volumes V are not available for most of the glaciers used in this analysis, but observations for 144 other valley glaciers demonstrate that [V] ? [S]γ with γ ≈ 1.36 (Reference Meier and BahrMeier and Bahr, 1996). Theoretical arguments show that γ = 1 + {(1 + m + 3r)/[5(q + 1)]} for valley glaciers where r is the slope scaling exponent mentioned in the introduction (Reference BahrBahr and others, 1997). (The characteristic slope [α] is related to glacier length by the closure condition [α] ? [x]-r .) In the past, r has been assumed zero for valley glaciers. In that case, when m = 1.70 (Equation (1)) and q + 1 = 1.61 (Equation (3)), the volume area scaling exponent is γ – 1.34, which is within 2% of the observed value.
The other OLS regression (m = 0.64) may be consistent with volume–area observations when r has a different value. If valley-glacier profiles have a roughly square-root shape (as commonly suggested for ice sheets (e.g. Reference PatersonPaterson, 1994)) then the slope exponent is r = 0.5. In that case, when m = 0.64 (the other OLS regression) and q + l = 1.61 (Equation (3)), then the volume–area scaling exponent is γ = 1.39, which is within roughly 2% of the observed value.
Similarly, the remaining OC regression (m = 1.04) is consistent with the volume–area scaling exponent as long as r ≈ 1/3. In that case, γ = 1.38. For r = 0–0.5 (a reasonable range (Reference BahrBahr and others, 1997)), other values of m between 0.5 and 2 will also agree with the volume–area observations. So until a belter slope–length scaling relation ran be established, volume–area scaling can support any of the proposed m.
The balance-rate scaling exponent m also plays a role in glacier response times. As detailed in Pfeffer and others (1997), smaller values of m imply that response times shorten for increasingly large glaciers. However, larger values of m imply that response times shorten with increasingly large glaciers. In particular, m = 0.64 (with r = 0.5) implies that larger glaciers have longer response times. On the Other hand, m = 1.7 (with r = 0) and m = 1.04 (with r = 1/3) both imply the less intuitive result that larger glaciers have shorter response limes. Actual data on response times are nearly non-existent, and another study, verified to some extent using Storglaciaren data, concludes that response times decrease with increasing glacier size (Reference Raper, Briffa and WigleyRaper and others, 1996). Basing the choice of m solely on intuition about response times could be misleading.
Most balance-rate profiles are concave down-glacier, positive at the head and negative at the terminus. Visually these balance profiles appear to be roughly quadratic (m ≈ 2). Such visual inspections can be misleading, however, and over a limited range, even a square root can be crudely approximated by a quadratic fit. Also, balance profiles are typically presented as a function of altitude, a rid not distance along the glacier as required for the closure condition. Additional data-compilation efforts could focus on converting existing balance–altitude data to balance–length relations by using observed area–altitude curves. The observed areas could be convened to lengths with the comparatively well-established area–length scaling relation (Reference BahrBahr, 1997b).
Conclusions
The characteristic glacier mass-balance rate (terminus balance rate) scales with glacier length and surface area. Larger glaciers have increasingly negative terminus balance rates. The trend is easily identified in Figures 1 and 2, although scatter in the data results in relatively low correlation coefficients. Only 68 valley and cirque glaciers are represented, and more terminus balance, length and area data are necessary to refine the fits. Without additional constraints, any of the fits in Table 1 might be reasonable.
Much of the preceding discussion supports a power-law relation ![]() with m ≈ 0.5–2. The data in Figures 1 and 2 can support any value of m within the range 0.64–1.7. The larger value of m ≈ 2 is consistent with glacier lengths being dependent on the mass-balance rate. Smaller values of m appeal to intuition about the physically plausible range of balance rates. However, all of the values between 0.64 and 1.7 are consistent with a previously derived volume–area scaling relation. Clearly, the presented data (which we believe to be the most complete currently available) are insufficient to determine the balance–length scaling exponent accurately. Until clearer arguments or additional data are presented, we conclude only that m = 0.5 and m = 2 are reasonable lower and tipper bounds.
with m ≈ 0.5–2. The data in Figures 1 and 2 can support any value of m within the range 0.64–1.7. The larger value of m ≈ 2 is consistent with glacier lengths being dependent on the mass-balance rate. Smaller values of m appeal to intuition about the physically plausible range of balance rates. However, all of the values between 0.64 and 1.7 are consistent with a previously derived volume–area scaling relation. Clearly, the presented data (which we believe to be the most complete currently available) are insufficient to determine the balance–length scaling exponent accurately. Until clearer arguments or additional data are presented, we conclude only that m = 0.5 and m = 2 are reasonable lower and tipper bounds.
Regardless of the exact value for the power-law scaling exponent, the analysis of the terminus mass-balance data supports the existence of a mass-balance-rate closure condition. By supporting its general validity, the closure condition ![]() can be used in theoretical analyses of volume scaling, response-time scaling and the derivation of other glacier parameters that are difficult to measure. Future analyses of the physical basis of the mass-balance closure condition could have tangible benefits for climate-change and sea-level-rise studies which make use of the volume and response-time scalings that depend on m. Although the data are not yet conclusive, this study is a first step in establishing bounds for m and focusing attention on the importance of mass-balance scaling. Given the wide-ranging social consequences of climate and sea-level scenarios, it is particularly important to continue making progress in establishing a value for the mass-balance scaling exponent.
can be used in theoretical analyses of volume scaling, response-time scaling and the derivation of other glacier parameters that are difficult to measure. Future analyses of the physical basis of the mass-balance closure condition could have tangible benefits for climate-change and sea-level-rise studies which make use of the volume and response-time scalings that depend on m. Although the data are not yet conclusive, this study is a first step in establishing bounds for m and focusing attention on the importance of mass-balance scaling. Given the wide-ranging social consequences of climate and sea-level scenarios, it is particularly important to continue making progress in establishing a value for the mass-balance scaling exponent.
Acknowledgements
We are grateful for the helpful reviews by R. LeB. Hooke, W. Tangborn, M. F. Meier and an exceptionally thorough anonymous referee who facilitated much of the preceding discussion. This work was supported by U.S. National Science Foundation grant OPP-9634289 to M. Dyurgerov.