1. INTRODUCTION
More than half a century after Voellmy (Reference Voellmy1955) published his heuristic bed-friction law for snow avalanches,
it is still at the heart of most avalanche flow models that are used in practical applications such as hazard mapping, the design of protection dams or dimensioning of buildings (e.g. Volk and Kleemayr, Reference Volk and Kleemayr1999; Sampl and Zwinger, Reference Sampl and Zwinger2004; Christen and others, Reference Christen, Kowalski and Bartelt2010).
S
b is the bed shear stress, σ
n the basal bed-normal stress,
![]() $ \bar{\hskip -0.9pt{\bi u}}$
the depth-averaged flow velocity, ρ the flow density, μ the dry-friction coefficient, and g/ξ a dimensionless ‘turbulent’ drag coefficient, with g the gravitational acceleration. Calibration work (e.g. Buser and Frutiger (Reference Buser and Frutiger1980); Gruber (Reference Gruber1998); Blagovechshenskiy and others (Reference Blagovechshenskiy, Eglit and Naaim2002)) and accumulated experience from practical application of the model led to recommended parameter pairs (μ, g/ξ) that vary strongly with avalanche size, assumed avalanche frequency, terrain form and altitude (Salm and others, Reference Salm, Burkard and Gubler1990; Christen and others, Reference Christen, Kowalski and Bartelt2010). Typical ranges are 0.15 < μ < 0.5 and 0.003 < g/ξ < 0.03, with some particular events needing even lower values of μ and/or higher values of ξ (see also (Ancey, Reference Ancey2012)). Recent high-resolution observations also show that such models cannot describe avalanche motion with constant coefficients (Köhler and others, Reference Köhler, McElwaine, Sovilla, Ash and Brennan2016). This indicates that the model does not correctly capture important physical mechanisms in snow avalanches, chief among them flow-regime transitions that alter the mechanisms generating friction and erosion and entrainment of the snow cover. (Issler and Gauer (Reference Issler and Gauer2008) illustrate the effect of flow-regime transitions. For the importance of erosion, see e.g. Eglit and Demidov (Reference Eglit and Demidov2005); Mangeney and others (Reference Mangeney2010).) A consequence is that such models cannot make predictions from a priori measurable data such as snow characteristics and topography (often called class-1 predictions in the engineering literature). Instead, an extensive calibration using past events is needed for each region in which one wishes to apply them.
$ \bar{\hskip -0.9pt{\bi u}}$
the depth-averaged flow velocity, ρ the flow density, μ the dry-friction coefficient, and g/ξ a dimensionless ‘turbulent’ drag coefficient, with g the gravitational acceleration. Calibration work (e.g. Buser and Frutiger (Reference Buser and Frutiger1980); Gruber (Reference Gruber1998); Blagovechshenskiy and others (Reference Blagovechshenskiy, Eglit and Naaim2002)) and accumulated experience from practical application of the model led to recommended parameter pairs (μ, g/ξ) that vary strongly with avalanche size, assumed avalanche frequency, terrain form and altitude (Salm and others, Reference Salm, Burkard and Gubler1990; Christen and others, Reference Christen, Kowalski and Bartelt2010). Typical ranges are 0.15 < μ < 0.5 and 0.003 < g/ξ < 0.03, with some particular events needing even lower values of μ and/or higher values of ξ (see also (Ancey, Reference Ancey2012)). Recent high-resolution observations also show that such models cannot describe avalanche motion with constant coefficients (Köhler and others, Reference Köhler, McElwaine, Sovilla, Ash and Brennan2016). This indicates that the model does not correctly capture important physical mechanisms in snow avalanches, chief among them flow-regime transitions that alter the mechanisms generating friction and erosion and entrainment of the snow cover. (Issler and Gauer (Reference Issler and Gauer2008) illustrate the effect of flow-regime transitions. For the importance of erosion, see e.g. Eglit and Demidov (Reference Eglit and Demidov2005); Mangeney and others (Reference Mangeney2010).) A consequence is that such models cannot make predictions from a priori measurable data such as snow characteristics and topography (often called class-1 predictions in the engineering literature). Instead, an extensive calibration using past events is needed for each region in which one wishes to apply them.
A number of attempts have been made to replace Eqn (1) by a formulation closer to the physics of granular media (Salm and Gubler, Reference Salm and Gubler1985; Norem and others, Reference Norem, Irgens, Schieldrop, Salm and Gubler1987; Gubler, Reference Gubler1989; Issler and Gauer, Reference Issler and Gauer2008), but they have only met with partial success and are rarely used in practice. Perhaps the most comprehensive and ambitious of these attempts is by Bartelt and co-workers, who set out to modify the Voellmy-type model RApid Mass MovementS (RAMMS; Christen and others, Reference Christen, Kowalski and Bartelt2010) with features suggested by the theory of granular flows, centred on what these authors term random kinetic energy (RKE). These papers can be characterised briefly as follows (we will refer to them henceforth as [I]–[VII]):
-
[I]: Buser and Bartelt (Reference Buser and Bartelt2009) [Production and decay of RKE in granular snow avalanches] introduce the notion of RKE, propose a balance equation for it and fit the model to experimentally observed velocity profiles. They also indicate an exponential dependence of Voellmy's friction parameter μ on RKE.
-
[II]: The RKE dependence is extended to g/ξ by Bartelt and Buser (Reference Bartelt and Buser2010) [Frictional relaxation in avalanches], who also discuss a number of conceptual issues.
-
[III]: Bartelt and others (Reference Bartelt, Meier and Buser2011) [Snow avalanche flow-regime transitions induced by mass and RKE fluxes] reduce the model sketched in [II] to a block model that can be described by ordinary differential equations and study its properties as a dynamical system (fixed points, stability, flow in phase space) in detail.
-
[IV]: In this paper, [Modelling mass-dependent flow-regime transitions to predict the stopping and depositional behaviour of snow avalanches], Bartelt and others (Reference Bartelt, Bühler, Buser, Christen and Meier2012) formulate the model from [II] as a depth-averaged model, solve it numerically and test it against a number of full-scale experiments.
-
[V]: In order to account for avalanche volume expansion due to particle collisions, Buser and Bartelt (Reference Buser and Bartelt2011) [Dispersive pressure and density variations in snow avalanches] develop equations for the vertical motion of the centre-of-mass of a control column in the avalanche under the action of what they call dispersive pressure.
-
[VI]: Extending the approach in [V], Buser and Bartelt (Reference Buser and Bartelt2015) [An energy-based method to calculate streamwise density variations in snow avalanches] supplement the model from [IV] with three further conservation equations connected to dispersive pressure.
-
[VII]: Bartelt and others (Reference Bartelt, Buser, Vera Valero and Bühler2016) [Configurational energy and the formation of mixed flowing/powder-snow and ice avalanches] equip the model introduced in [VI] with a second layer for the powder-snow cloud and propose that the latter is formed by intermittent ejection of a mixture of fine snow grains with air from the dense core.
Recently, Bartelt and Buser (Reference Bartelt and Buser2016) applied their approach to debris flows. We chose not to include that paper in the present discussion because Iverson and George (Reference Iverson and George2016) already provided a concise critique of the way the authors use the notions of excess pore pressure and particle–fluid interactions.
These seven papers use non-standard terminology in many instances. To help readers who read the original papers [I]–[VII] alongside the present analysis, we will use that terminology most of the time. However, it may be useful to establish correspondence with standard terminology in advance for a few key terms:
Random kinetic energy: ‘Fluctuation energy’ or ‘granular temperature’ are established notions to describe the same phenomenon. There is a potential pitfall in the definition given, e.g., in [VII], which reads ‘…the kinetic energy associated with all particle movements different from the mean velocity of the flow’. Apparently, the mean velocity is to be understood as the velocity averaged over both time and the flow depth. In shear flows, a large part of this energy is not random, but due to the non-uniformity of the mean velocity profile. In [I] and [II], no depth-averaging is involved and velocity profiles are explicitly discussed. There is also ambiguity since fluctuation energy can be present at the grain scale (granular temperature) or at an eddy scale (turbulent kinetic energy).
Dispersive pressure: This is taken to mean the excess of the slope-normal stress at the base over the slope-normal component of the depth-integrated weight; it is positive when the avalanche dilutes and negative when it contracts. Readers familiar with the literature on snow avalanche dynamics should note that the same term was used a quarter century earlier by Norem and others (Reference Norem, Irgens, Schieldrop, Salm and Gubler1987, Reference Norem, Irgens and Schieldrop1989) to designate the (always positive) pressure due to particle collisions. Iverson and George (Reference Iverson and George2016) also discuss the notion of dispersive pressure in the context of a follow-up paper by Bartelt and Buser (Reference Bartelt and Buser2016) on debris-flow modelling.
Configuration energy: This is a central notion in [VI]. It is otherwise probably most often used in the context of atomic and many-body physics, where it describes the potential energy of the system due to the mutual interactions between its components (usually by means of electromagnetic forces). In the context of [VI] and [VII], it is simply the depth-integrated gravitational potential energy density of the avalanche core relative to densest random packing.
Plumes: In [VII], the authors use this term for puffs of the air–snow mixture that are ejected near the avalanche front. ‘Plume’ has a standard, technical meaning in fluid dynamics, namely a column of one fluid moving through another. In the extensive literature on gravity currents, ‘plume’ usually refers to the entire gravity current on an incline, e.g. see (Simpson, Reference Simpson1987). What the authors are describing is simply turbulent entrainment by eddies.
So far, these models have not been discussed in the literature by other workers. Given the wide-spread use of RAMMS and the prospect of the proposed extensions being moved into the production version, a critical assessment of the physical foundation of the models and their mathematical implementation is called for. Our analysis of the papers [I]–[VII] revealed that the model assumptions have a number of important implications that appear not to have been recognised earlier. Also, we found that a number of fundamental equations in the earlier papers were tacitly corrected in later papers, which can make the reading confusing at times. Yet, we believe there remain problems with the proposed mechanisms, regarding both their physical plausibility and their mathematical formulation, that need to be addressed before the model can be applied to practical problems with confidence.
We will first discuss the concept and mathematical formulation of the base model without density variation [I]–[IV] in Section 2, then scrutinise its extension to variable density [V]–[VII] in Section 3. We consider the problems posed by the suspension layer (powder-snow cloud) in [VII] separately in Section 4 and conclude with suggestions for further work in Section 5. Technical details are relegated to the appendices. Due to space constraints, the present paper cannot be completely self-contained. We reproduce key equations and attempt to summarise the argumentation of the authors, but refer the readers to the original papers for details and precise wording.
2. THE BASIC RKE MODEL
There are significant differences in the mathematical formulation of some key concepts between the papers [I]–[IV]. Our analysis in this section will concentrate on a comparison between the Voellmy friction law, the RKE-modified friction law – most succinctly proposed in [III] and [IV] – and an example from the kinetic theory for granular materials, adapted from (Jenkins and Askari, Reference Jenkins and Askari1999). Papers [I] and [II] contain several conceptual errors that were tacitly corrected in [IV]; as they do not affect the formulation of the model directly, but have led to confusion among readers, we will briefly discuss them in Appendix A.
2.1. Summary of model assumptions
Paper [IV] starts from the long-established depth-averaged balance equations of mass and momentum. For the earliest formulation in snow-avalanche dynamics, see (Eglit, Reference Eglit1968; Plam and others, Reference Plam, Radok and Taylor1984). Parker and others (Reference Parker, Fukushima and Pantin1986) give a detailed derivation in a two-layer situation similar to the one discussed in Section 4. In a coordinate system following the terrain, these equations read as follows if terms due to non-orthogonality and curvature (Gray and others, Reference Gray, Wieland and Hutter1999; Gray, Reference Gray2001; Bouchut and Westdickenberg, Reference Bouchut and Westdickenberg2004) are neglected:
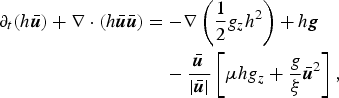 $$\eqalign{\partial_t \lpar h\hskip 0.9pt{\bar{\hskip -0.9pt{\bi u}}}\rpar + {\bf \nabla} \cdot \lpar h\hskip 0.9pt {\bar{\hskip -0.9pt{\bi u}}}\hskip 0.9pt {\bar{\hskip -0.9pt{\bi u}}}\rpar = & -\!{\bf \nabla} \left({1\over 2} g_{z} h^{2} \right) + h {\bi g} \cr & - {{\bar{\hskip -0.9pt{\bi u}}} \over \vert \hskip 0.9pt{\bar{\hskip -0.9pt{\bi u}}}\vert} \left[\mu h g_z + {g\over \xi} \hskip 0.9pt{\bar{\hskip -0.9pt{\bi u}}}^2 \right]\comma }$$
$$\eqalign{\partial_t \lpar h\hskip 0.9pt{\bar{\hskip -0.9pt{\bi u}}}\rpar + {\bf \nabla} \cdot \lpar h\hskip 0.9pt {\bar{\hskip -0.9pt{\bi u}}}\hskip 0.9pt {\bar{\hskip -0.9pt{\bi u}}}\rpar = & -\!{\bf \nabla} \left({1\over 2} g_{z} h^{2} \right) + h {\bi g} \cr & - {{\bar{\hskip -0.9pt{\bi u}}} \over \vert \hskip 0.9pt{\bar{\hskip -0.9pt{\bi u}}}\vert} \left[\mu h g_z + {g\over \xi} \hskip 0.9pt{\bar{\hskip -0.9pt{\bi u}}}^2 \right]\comma }$$
where
![]() $\bar {{\bi u}} = (u,\,v)^{\rm T}$
, ∇ = (∂
x
, ∂
y
) and
g
= (g
x
, g
y
)T denote the depth-averaged mean flow velocity, the two-dimensional (2-D) gradient operator, and the slope-parallel components of the gravitational acceleration vector, respectively. Finally, h is the flow depth, and Q is the volumetric entrainment rate, which we will not discuss here. Incidentally, Eqn (3) assumes
$\bar {{\bi u}} = (u,\,v)^{\rm T}$
, ∇ = (∂
x
, ∂
y
) and
g
= (g
x
, g
y
)T denote the depth-averaged mean flow velocity, the two-dimensional (2-D) gradient operator, and the slope-parallel components of the gravitational acceleration vector, respectively. Finally, h is the flow depth, and Q is the volumetric entrainment rate, which we will not discuss here. Incidentally, Eqn (3) assumes
![]() $\overline {\hskip -0.9pt{\bi uu}} \approx \hskip 0.9pt{\bar {\hskip -0.9pt{\bi u}}}\hskip 0.9pt{\bar {\hskip -0.9pt{\bi u}}}$
, i.e., a uniform velocity profile. This is a poor approximation if RKE is important, as the velocity profiles presented in [I] show.
$\overline {\hskip -0.9pt{\bi uu}} \approx \hskip 0.9pt{\bar {\hskip -0.9pt{\bi u}}}\hskip 0.9pt{\bar {\hskip -0.9pt{\bi u}}}$
, i.e., a uniform velocity profile. This is a poor approximation if RKE is important, as the velocity profiles presented in [I] show.
The basic RKE model departs from standard Voellmy-type models such as RAMMS in that the friction parameters μ and g/ξ in Eqn (3) are postulated to depend on R K , the RKE density due to fluctuations of the particle velocities about their mean values, as
With R 0, a new parameter enters the model that needs to be determined empirically. A further balance equation describing advection, production and dissipation of RKE complements the balance equations shown above:
where S b is the bed shear stress given by the second line in (3), and 0 < α < 1, β > 0 are two parameters. Crucial ingredients of the model are the production and dissipation terms for R K as well as the postulated dependence of the Voellmy friction parameters (Eqn (4)).
While papers [I]–[IV] refer to the kinetic theory of granular flows, they depart from one of its well-established results without mentioning or justifying their choice: both for dilute and dense granular flows (and also for turbulent fluid flows), the dissipation rate is found to grow as R K 3/2 (Jenkins and Richman, Reference Jenkins and Richman1985; Jenkins and Berzi, Reference Jenkins and Berzi2010). This is known as Haff's law and is a basic result of kinetic theory (Haff, Reference Haff1983). If dissipation is assumed to grow only linearly with R K as in Eqn (5), much higher equilibrium values of R K result for a given production rate. Equation (5) contains another strong assumption for which no justification is given, namely that a fixed fraction of the shear dissipation rate is converted into RKE.
2.2. Velocity dependence of the effective friction coefficient in the RKE model
From Eqns (4) and (5), one can deduce the speed of steady, uniform flow for a given slope angle θ and flow depth h, and thus the effective friction law: the left-hand side of Eqn (5) vanishes in steady, uniform flow so that
For simplicity, let us define
![]() $U \equiv \vert\bar {{\bi u}}\vert$
, the non-dimensional RKE r ≡ R
K
∞/R
0, the velocity scale
$U \equiv \vert\bar {{\bi u}}\vert$
, the non-dimensional RKE r ≡ R
K
∞/R
0, the velocity scale
and the effective Voellmy friction coefficient,
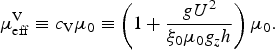 $$ \mu_{\rm eff}^{\rm V} \equiv c_{\rm V}\mu_0 \equiv \left(1 + {g U^2 \over \xi_0 \mu_0 g_z h} \right)\mu_0. $$
$$ \mu_{\rm eff}^{\rm V} \equiv c_{\rm V}\mu_0 \equiv \left(1 + {g U^2 \over \xi_0 \mu_0 g_z h} \right)\mu_0. $$
This brings Eqn (6) into the form
which is solved by
W0 is the upper branch, defined on (−e−1, ∞), of Lambert's W function, which is the solution to x = W(x) exp (W(x)). As x → ∞, also W(x) → ∞, but for x > e, W(x) < ln x. Applying this to Eqn (4) and carrying out a few algebraic manipulations involving the defining equation of W(x), we can rewrite the effective friction coefficient of the RKE model in steady, uniform flow as
2.3. Comparison with kinetic theory
It is interesting to compare this heuristic bed-friction law to one derived using methods of the kinetic theory for collisional grain flows. We consider an essentially passive slab that is suspended and transported on a relatively thin region of intensely sheared grains at its base (Jenkins and Askari, Reference Jenkins and Askari1999). This may represent a slab avalanche in a very early phase, when the slab is only about to disintegrate and is gliding on the thin weak layer whose collapse caused the avalanche to release. We do not propose this model as a replacement for any other model, but have chosen it because it describes the same flow configuration as the Voellmy model (Salm, Reference Salm1993), namely a deformable but essentially passive heap riding on a thin, intensely sheared basal layer. Yet, the Jenkins–Askari model shows distinctly different behaviour from both the original Voellmy model or the basic RKE model of [IV].
Expressions for the shear stress, normal stress, energy flux and rate of collisional dissipation at the base result from detailed consideration of the transfer of momentum and energy in particle collisions with a bumpy, rigid boundary (Richman, Reference Richman1988). Their values are obtained as solutions of boundary value problems for the RKE and average particle velocity in the thin region of intense shearing at the base. The resulting expression for the dynamic, or rate-dependent part, of the ratio of the shear stress, S, and normal stress, P, at the base, when added to the rate-independent part, μ 0, gives the effective friction coefficient (Jenkins and Askari, Reference Jenkins and Askari1999):
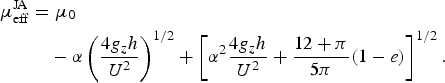 $$\eqalign{\mu_{\rm eff}^{\rm JA} & = \mu_0 \cr & \quad - \alpha \left({4g_z h\over U^2}\right)^{1/2} + \left[\alpha^2{4g_z h\over U^2} + {12+\pi\over 5\pi}\lpar 1-e\rpar \right]^{1/2}.}$$
$$\eqalign{\mu_{\rm eff}^{\rm JA} & = \mu_0 \cr & \quad - \alpha \left({4g_z h\over U^2}\right)^{1/2} + \left[\alpha^2{4g_z h\over U^2} + {12+\pi\over 5\pi}\lpar 1-e\rpar \right]^{1/2}.}$$
Here, α measures the difference between slip working and collisional dissipation at the boundaries; it is a function of the boundary roughness and the coefficient of restitution, e w, in a collision between a flow sphere and the boundary. e is the coefficient of restitution in a collision between two particles in the flow. Note that the model is restricted to low and moderate velocities so that the slab on top of the thin shear layer does not become strongly agitated.
Figure 1 compares the velocity dependence of the effective friction coefficient of the original Voellmy friction law (in two different calibrations), the kinetic theory and the RKE-enhanced Voellmy model. Note that these curves are valid only for the specific choice of parameters. For all friction laws, we chose a slope angle of 30° and a flow depth of 1 m. For the Voellmy model, we set μ = 0.15 and g/ξ = 0.0049 in the usual calibration, but μ = 0.4 and g/ξ = 0.00018 in the calibration proposed by Gauer (Reference Gauer2014). For the Jenkins–Askari model, we selected μ 0 = 0.4, volume fraction at the base ν 0 = 0.45, and restitution coefficients e = 0.85 inside the shear layer and e w = 0.80 at its boundaries. Assuming a rough boundary of smaller particles, we set α = 0.463. For the RKE model, μ 0 = 0.4, g/ξ 0 = 0.017, α = 0.1, β = 0.5 s−1 and R 0/ρ = 15 m2 s−2 were assumed. With the traditional calibration of the Voellmy model, the resistance is dominated by the velocity-dependent term already at speeds of 15–20 m s−1 so that the model generally underpredicts avalanche velocities substantially. This defect is mitigated in Gauer's calibration – at the expense of an almost linear dependence of μ on the mean slope angle of the path and a linear dependence of ξ on the drop height (Gauer, Reference Gauer2014). The Jenkins–Askari model exhibits rapid growth of μ eff at low velocity, but moderate growth at high velocity, thus allowing the avalanche to reach high velocity even on moderately steep slopes. Finally, the RKE model shows completely different, non-monotonic behaviour, with μ eff decreasing with increasing velocity above some threshold speed. We caution, however, that Fig. 1 takes the models beyond their range of applicability. Within the realistic range 0–60 m s−1, a constant value μ ≈ 0.42 and g/ξ = 0 – corresponding to the Savage–Hutter model (Savage and Hutter, Reference Savage and Hutter1989, Reference Savage and Hutter1991) – would give fairly similar behaviour.
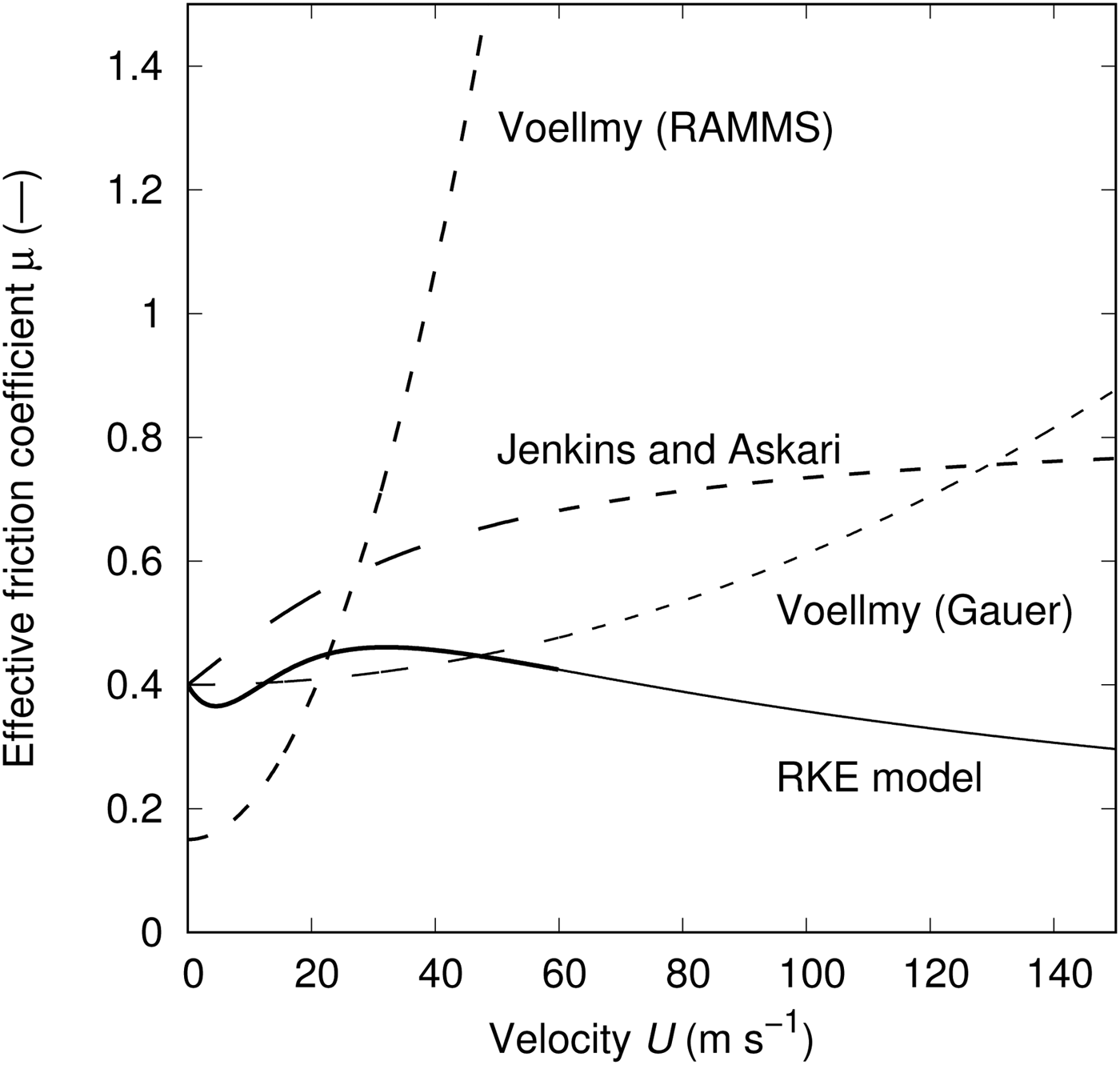
Fig. 1. Comparison of the velocity dependence of the effective friction coefficient for an avalanche with flow depth 1 m on a 30° slope. (i) Voellmy model with traditional calibration (Christen and others, Reference Christen, Kowalski and Bartelt2010), μ = 0.15, g/ξ = 0.0049. (ii) Voellmy model with the calibration suggested by Gauer (Reference Gauer2014), for an average slope angle β ≈ 30°: μ 0 = 0.4, g/ξ = 0.00018. (iii) Jenkins and Askari (Reference Jenkins and Askari1999) model with μ 0 = 0.4, ν 0 = 0.45, e = 0.85, e w = 0.8 and α = 0.463. (iv) RKE model [IV] with μ 0 = 0.4, g/ξ 0 = 0.017, α = 0.1, β = 0.5 s−1 and R0/ρ = 15 m2 s−2.
The Jenkins–Askari model predicts that stationary flows are only possible in a limited range of slope angles (22°–38° for the choice of parameters in Fig. 1). The original Voellmy law (1) clearly has a lower bound
![]() $\theta \geq \arctan \mu $
, but no upper bound because μ
eff grows as the square of the velocity. A stationary flow can thus be attained in arbitrarily steep terrain. From Figure 1, one can infer the following scenario in the RKE model: an avalanche starting in sufficiently steep terrain will quickly attain high velocity and low effective friction. If the slope angle decreases in such a way that always tanθ(x) ≳ μ
eff
RKE(U(x)), the avalanche will continuously accelerate while the slope angle tends to 0. Of course, slopes on Earth are too short for this to happen, but the theoretical possibility illustrates that Eqn (4) is an extremely strong assumption.
$\theta \geq \arctan \mu $
, but no upper bound because μ
eff grows as the square of the velocity. A stationary flow can thus be attained in arbitrarily steep terrain. From Figure 1, one can infer the following scenario in the RKE model: an avalanche starting in sufficiently steep terrain will quickly attain high velocity and low effective friction. If the slope angle decreases in such a way that always tanθ(x) ≳ μ
eff
RKE(U(x)), the avalanche will continuously accelerate while the slope angle tends to 0. Of course, slopes on Earth are too short for this to happen, but the theoretical possibility illustrates that Eqn (4) is an extremely strong assumption.
It has been known for a long time that the shear stress in rapidly sheared granular materials increases with the square of the shear rate if the volume is held constant. If the experiment is carried out at constant normal stress (as in free-surface chute flows), the shear stress increases also, but much more slowly due to the material expanding. For example, experiments on a wide range of slope angles (Holyoake and McElwaine, Reference Holyoake and McElwaine2012) show that the effective friction always increases with velocity for a fixed flow rate. Kinetic theory successfully predicts this behaviour.
It is conceivable that one sometimes can obtain satisfactory simulations of observed events if completely different mechanisms have a similar friction-reducing effect, e.g., lubrication by a thin water layer, progressive comminution of snow particles or excess pore pressure. However, if the objective is to construct a physically founded model of snow avalanche motion, it appears more promising to adopt the key results from the theory of granular flows and to add such non-granular effects in a more specific manner.
2.4. Comparison with experiments
Paper [IV] points out that chute experiments with snow (Platzer and others, Reference Platzer, Bartelt and Kern2007) show significantly smaller ratios of basal shear stress S to basal normal stress N in the head of the flows than at the snout and in the tail. The authors attribute this difference to different levels of RKE and argue that, therefore, a separate balance equation for RKE is needed. However, this conclusion does not follow: the entire flow mass started from rest simultaneously, so its flow depth, velocity and RKE should evolve in the same way unless some other process differentiates between head and tail. Longitudinal normal stresses reinforce gravity at the snout and counteract it in the tail, leading to a significant decrease of the velocity from snout to tail (Platzer and others, Reference Platzer, Bartelt and Kern2007). Thus, a shear-rate-dependent rheology may also be able to capture the observed variation in the ratio of shear stress to normal stress.
There is, however, a finding from the chute experiments (Platzer and others, Reference Platzer, Bartelt and Kern2007) that deserves closer consideration: independent of whether the flow is stationary or not, S/N is the effective bed friction coefficient, μ eff. The snow chute experiments indicate that μ eff is higher in the slower tail than in the faster head, while the snout, which moves at the same speed as the head, also has a high value of μ eff. This appears to be in stark contrast to the findings of the granular–flow experiments and the granular rheology, in which μ eff increases monotonically with the velocity. It should be illuminating to reanalyse the snow-chute experiments in terms of granular rheology in order to confirm or refute the discrepancy with the granular experiments. One may then try to relate the variation of μ eff to, e.g., the dominant particle size at different locations in the flow.
2.5. Is a dynamical equation for RKE necessary?
Another interesting question is whether the extra balance equation for RKE is really necessary. Certainly, it is needed in a complete theory of granular flows because RKE (or granular temperature) may be produced at one location, transported by advection and diffusion, and finally dissipated somewhere else. Bartelt and co-workers emphasise that RKE is produced at the bed interface and diffuses into the avalanche body. Much of the RKE is certainly produced near the bed, where the shear rate is highest, but in highly agitated flows with a Bagnold-type velocity profile, significant RKE production occurs also inside the flow so that bed-normal diffusion of RKE need not play a dominant role in the balance equation. In fact, kinetic theory shows that boundary effects decay exponentially, with a decay length that is only a few particles long for dense inelastic flows. This means the equilibrium granular temperature is slaved to the local shear rate with an extremely rapid relaxation time. Moreover, the flow model is depth-averaged and bed-normal RKE diffusion is not directly visible in the model; this makes it much less compelling to use an extra equation for RKE unless the dissipation coefficient β is very small, which hardly can be the case in a dense granular flow with rather inelastic collisions. Typical values of the inverse RKE decay constant 1/β ≳ 1 s used in [IV] are short compared with the macroscopic timescale of avalanche flow, i.e., the RKE is almost always close to its instantaneous equilibrium value. In addition, it is inconsistent to include a process with such rapid relaxation while excluding processes with much slower relaxation.
The RKE model, using the Voellmy friction law as a basis, inherits from it the general disadvantage that it only specifies the basal shear stress. If the shear stress inside the flowing material or the normal stresses are needed, then additional assumptions have to be made. Bartelt and others (Reference Bartelt, Buser and Platzer2006) assume the Voellmy model for the basal shear stress, a viscous-frictional model inside the flow and an exponential decrease of the RKE with distance from the bed in order to approximate velocity profiles measured at the test site, Vallée de la Sionne. In particular, these rheological assumptions determine the bed-normal stresses inside the flow. This approach was, however, abandoned in subsequent papers.
3. THE VARIABLE-DENSITY MODEL
Paper [V] marks an important turning point relative to [I]–[IV] at the conceptual level: it acknowledges – albeit somewhat ambiguously – that RKE can do work expanding the flow in the bed-normal direction:
In general, the energy, R, is random in nature and therefore R cannot perform mechanical work. However, at the base of the avalanche a flux of R is deflected by the running surface upwards into the segment [a bed-normal control volume across the depth of the avalanche] (…). The granular burst is given by the flux,
![]() $\dot{\hskip -0.9ptR}$
. This energy flux raises the center of mass, converting a random energy flux into potential energy (it performs mechanical work).
$\dot{\hskip -0.9ptR}$
. This energy flux raises the center of mass, converting a random energy flux into potential energy (it performs mechanical work).
In fact, it is a fundamental property of agitated granular masses that the random particle motion creates stresses inside the mass and at solid boundaries. Where particle impacts move a boundary against an externally applied force or where stress gradients inside the granular flow accelerate a portion of the mass, the granular mass performs mechanical work. This process is analogous to the conversion of internal energy (heat), associated with random molecular motion, in a combustion engine.
In [V], the emphasis is on the bed-normal motion of a column of avalanching snow with constant mass hold-up; RKE is assumed given. Paper [VI] extends this mass-point or infinite-slope model to a complete flow model, with a dynamical equation for the RKE. In [VI], there are a few changes in the equations for bed-normal motion (or, equivalently, density change) due to the newly introduced concept of configuration energy, which is defined as the difference in depth-integrated gravitational potential energy relative to a completely settled configuration at the same location on the slope.
Buser and Bartelt decompose the bed-normal stress at the bed, N (b), into the weight-induced part N g (b) = ρ g z h ≡ mg z with m the constant mass hold-up (or mass per unit footprint area) in this idealised situation, and the dispersive (or excess) pressure N K (b), which is proportional to the bed-normal acceleration of the centre-of-mass position k. With slightly changed notation,
Assuming a uniform density profile, one may approximate k = h/2. At this point, a constitutive equation specifying N
(b) (or N
K
(b)) in terms of the flow variables h (or k),
![]() $\hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}$
and R
K
is needed. In [V] and [VI], Buser and Bartelt pursue two different approaches, which we will examine in turn.
$\hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}$
and R
K
is needed. In [V] and [VI], Buser and Bartelt pursue two different approaches, which we will examine in turn.
3.1. The approach of [V]: analogy with an ideal gas.
In the text following (V.6), Buser and Bartelt postulate that the equation of state of a granular snow avalanche is essentially equivalent to that of an ideal gas, i.e., they assume
in their notation. Next, they take a total time derivative of the equation of motion (V.4) to arrive at (V.5) and then do the same with the equation of state shown above. However, in doing so, they only keep
![]() $\gamma\hskip 0.9pt \dot{\hskip -0.9pt R}_K h$
on the right-hand side and omit
$\gamma\hskip 0.9pt \dot{\hskip -0.9pt R}_K h$
on the right-hand side and omit
![]() $\gamma R_K {\dot h}$
:
$\gamma R_K {\dot h}$
:
With
![]() ${\hskip2pt}\dot {{\hskip-2pt}N}_g^{(b)} \equiv 0$
and
${\hskip2pt}\dot {{\hskip-2pt}N}_g^{(b)} \equiv 0$
and
![]() ${\hskip2pt}\dot {{\hskip-2pt}N}_K^{(b)} \equiv {\dot {{\hskip-2pt}N}}^{(b)}$
, this mathematical error leads to the third-order equation adopted in [V],
${\hskip2pt}\dot {{\hskip-2pt}N}_K^{(b)} \equiv {\dot {{\hskip-2pt}N}}^{(b)}$
, this mathematical error leads to the third-order equation adopted in [V],
Indeed, if one used Eqn (11) in (V.4) and set N K (b) = N (b) + mg z (note that g z < 0), one would immediately arrive at the second-order equation
As the avalanche expands perpendicularly to the bed, the RKE density R K tends to decrease both because the energy is distributed over a larger volume and energy is expended in working against gravity.
A more detailed analysis of the analogy between thermodynamics and the kinetic theory of granular materials suggests to replace the constant γ by a function of the particle volume fraction, f(ν). This function depends on the details of the particular approximation one chooses. Using ν = ν
0
k
0/k, we can express f(ν) in terms of k as
![]() $\tilde{\hskip -0.9pt f}(k) = f(\nu _0 k_0 / k)$
and replace γ with
$\tilde{\hskip -0.9pt f}(k) = f(\nu _0 k_0 / k)$
and replace γ with
![]() $\tilde{\hskip -0.9pt f}(k)$
in Eqn (12).
$\tilde{\hskip -0.9pt f}(k)$
in Eqn (12).
3.2. The approach of [VI]: configuration energy
Paper [VI] arrives at Eqn (VI.25), which is essentially equivalent to (V.7), without invoking analogy with an ideal gas or making an explicit assumption for the constitutive equation; hence, we need to discuss this approach separately. As mentioned above, an important difference between [V] and [VI] is the use of energy balances throughout [VI]. In particular, the notion of configuration energy density (CED), R
V
, is introduced. In [VI], Section 3, it is defined as the gravitational potential energy per unit volume, averaged over the depth of a bed-normal column, relative to the configuration with maximum random packing at the same location. Buser and Bartelt introduce the production rate of CED,
![]() $\hskip 0.9pt \dot{\hskip -0.9pt P}_V$
, and postulate it to be a fixed fraction γ of the net production rate of the sum of RKE and CED.
$\hskip 0.9pt \dot{\hskip -0.9pt P}_V$
, and postulate it to be a fixed fraction γ of the net production rate of the sum of RKE and CED.
The critical step of their derivation is described between Eqns (VI.20) and (VI.21), which we quote here (note that the authors switched notation from h to V Φ, but we will use h in what follows):
The total work done per unit time by the normal pressure at the bottom of the avalanche N […] must be in balance with the total working of the particle interactions per unit volume. We have termed this change in potential energy as the configurational energy production
![]() $\hskip 0.9pt \dot{\hskip -0.9pt P}_V$
. Therefore, the total change in the volume is
$\hskip 0.9pt \dot{\hskip -0.9pt P}_V$
. Therefore, the total change in the volume is
Equation (VI.21) above is identical with (V.6) if one identifies the coefficients γ in [V] and [VI] with each other, extends R
K
in (V.6) to R = R
K
+ R
V
= R
K
/(1 − γ), and replaces the partial time derivative ∂
t
with the advective derivative D
t
≡ ∂t
+u⋅∇ to account for the translational motion of the control volume. We find this text passage somewhat ambiguous, but understand it as making the following interrelated statements: (i) At the mesoscopic level, particle interactions in the avalanche do mechanical work, which manifests itself as (and is quantitatively equal to) the mechanical work done by the basal pressure at the macroscopic level. (ii) The rate of mechanical work done by the pressure due to particle collisions must be equal to the rate of change of the configuration energy. (iii) The work rate of the bed pressure is D
t
(Nh). The paragraphs below will analyse these three statements in detail. Note that we will henceforth write P
V
instead of
![]() $\dot {P}_V$
used by Bartelt and co-workers. Their notation suggests that the production rate is the time derivative of some other quantity, which, however, is never introduced and would have no other meaning than the total of the RKE produced in an advected unit volume – in particular, it is not the RKE.
$\dot {P}_V$
used by Bartelt and co-workers. Their notation suggests that the production rate is the time derivative of some other quantity, which, however, is never introduced and would have no other meaning than the total of the RKE produced in an advected unit volume – in particular, it is not the RKE.
3.3. Pressure, work rate and configuration energy
The first issue to note is that, contrary to the statement (i) above, the pressure at the bottom does not do mechanical work because the bed-normal velocity w(0) vanishes at that boundary. At the top surface, w(h) ≠ 0, but the pressure (relative to atmospheric pressure) vanishes. The mechanical work is being done inside the mass, where w(z) ≠ 0 and N(z) ≠ 0. This is not merely a semantic point because it leads to extra coefficients in the expression for the work rate that are missing on the left-hand side of Eqn (VI.21). We will detail this after mentioning the remaining issues.
Second, statement (ii) neglects the change of kinetic energy associated with bed-normal motion that unsteady expansion necessarily induces. A third issue is intertwined with this one: the text as well as Eqn (VI.21) set the change in configuration potential energy equal to the work done by the total pressure N = N
g
+ N
K
(statements (ii) and (iii) combined). However, only N
g
(z) contributes to the change of CED, whereas the gradient of dispersive pressure, ∂z
N
K
, accelerates the avalanching mass in the z-direction and changes the corresponding contribution to the kinetic energy density
![]() ${\cal K}_z \equiv \overline {\rho w^2}/(2\,h)$
.
${\cal K}_z \equiv \overline {\rho w^2}/(2\,h)$
.
Fourth, Eqn (VI.21) stipulates that the work rate of the pressure is D
t
(Nh); no further explanation for this assertion is given. The expression D
t
(Nh) contains the three terms
![]() $\dot {N}_K h$
,
$\dot {N}_K h$
,
![]() $N_g {\dot h}$
and
$N_g {\dot h}$
and
![]() $N_K {\dot h}$
(
$N_K {\dot h}$
(
![]() $\hskip 1pt \dot{\hskip -1pt N}_g h$
is zero if there is no net mass flux into or out of the control volume). If Eqn (VI.21) were true, pressure would do mechanical work whenever it increases, even if h is held constant. A simple example is heating of a gas in a rigid container: the gas does not do mechanical work in this process, but its capacity to do so increases.
$\hskip 1pt \dot{\hskip -1pt N}_g h$
is zero if there is no net mass flux into or out of the control volume). If Eqn (VI.21) were true, pressure would do mechanical work whenever it increases, even if h is held constant. A simple example is heating of a gas in a rigid container: the gas does not do mechanical work in this process, but its capacity to do so increases.
In Appendix B, we will compare the model [VI] to the general balance equations for mass, momentum and fluctuation energy in a depth-averaged flow model. It may be instructive, however, first to illustrate the issues mentioned above in a simple, quasi-1-D setting, disregarding variations in the x- and y-directions. We assume, however, that shearing motion in these directions produces RKE. The control volume under consideration and the stresses and body forces in the z-direction are schematically represented in Fig. 2. We first consider the momentum balance and then turn attention to the energy balance.
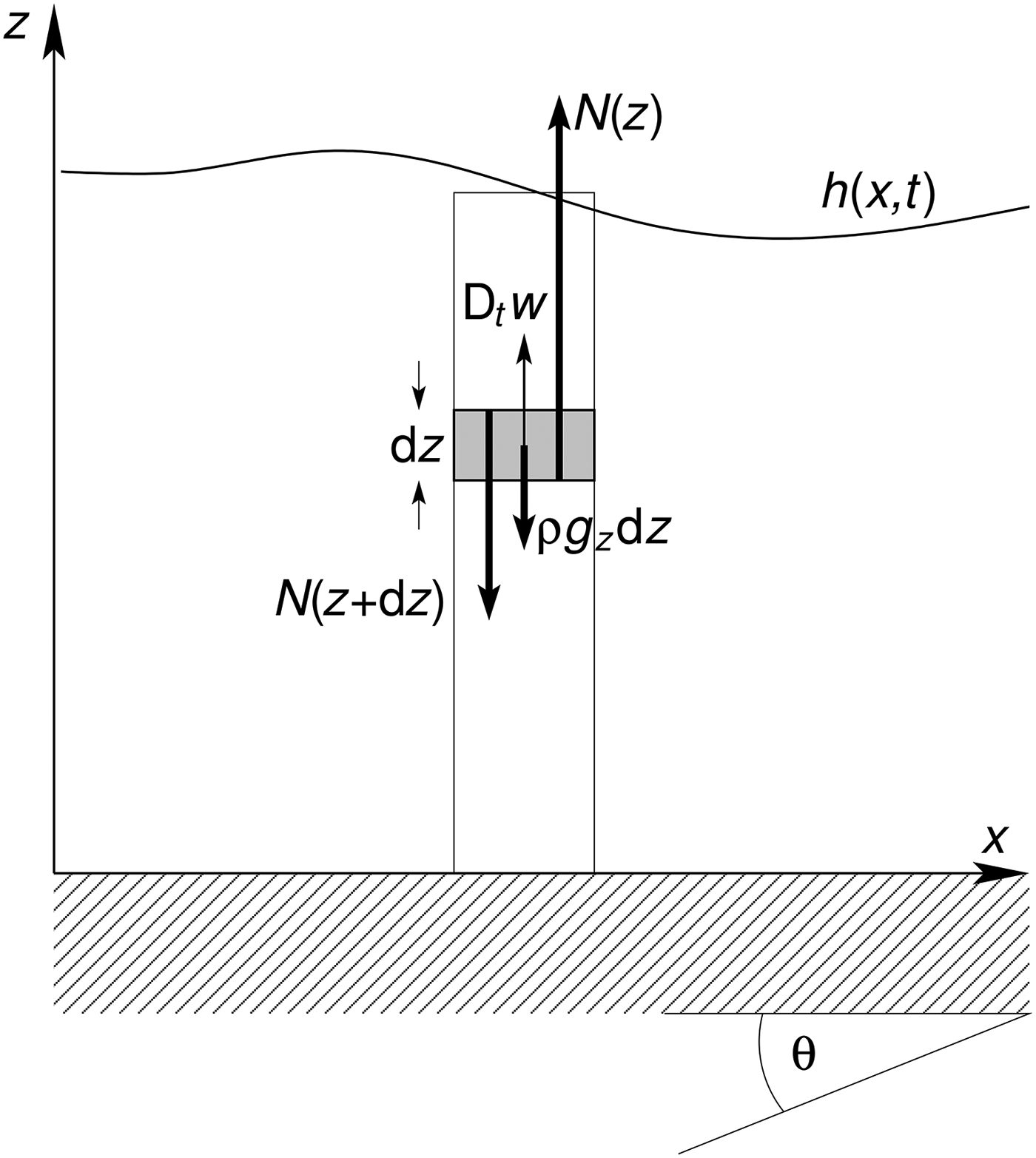
Fig. 2. Schematic representation of an infinitesimally thin column of an avalanche on a plane inclined at an angle θ and an infinitesimal control volume within that column. Only the forces relevant for the bed-normal motion are indicated.
The momentum balance for a thin slope-parallel slice of thickness dz at height z is given by
Integrating this equation over z from 0 to ∞, using the boundary conditions ρ(∞) = w(0) = N(∞) = 0 and introducing the mass hold-up
![]() $m \equiv \int \rho (z) {\rm d} z$
as well as the centre-of-mass velocity
$m \equiv \int \rho (z) {\rm d} z$
as well as the centre-of-mass velocity
![]() $\bar {w} \equiv \int \rho w {\rm d} z$
, one obtains
$\bar {w} \equiv \int \rho w {\rm d} z$
, one obtains
where N
(b) is the value of N at the bed. If one assumes the density to be uniform across the flow depth but variable in time,
![]() $w(z,\,t) = 2 \bar {w}(t) z/h$
for kinematic reasons. Similarly,
$w(z,\,t) = 2 \bar {w}(t) z/h$
for kinematic reasons. Similarly,
![]() $ \hskip 0.9pt\dot{\hskip -0.9pt w}(z,t) \equiv (\partial_t + w(z ,t ) \partial_z)w(z , t)= 2 {\dot {\bar w}}(t) z/h$
in the Lagrangean sense. The dynamics, governed by Eqn (13), then requires the pressure to vary with ζ ≡ z/h as
$ \hskip 0.9pt\dot{\hskip -0.9pt w}(z,t) \equiv (\partial_t + w(z ,t ) \partial_z)w(z , t)= 2 {\dot {\bar w}}(t) z/h$
in the Lagrangean sense. The dynamics, governed by Eqn (13), then requires the pressure to vary with ζ ≡ z/h as
The kinetic and configuration energies are given by
If the density profile is uniform, these energies become
We can calculate the depth-integrated work rate
![]() $ \hskip 0.9pt\dot{\hskip -0.9pt W}$
from the well-known expression for the work rate per unit volume,
$ \hskip 0.9pt\dot{\hskip -0.9pt W}$
from the well-known expression for the work rate per unit volume,
![]() $\hskip 1pt\dot{\hskip -2.4pt{\cal W}}$
, of the internal (Cauchy) stresses in a continuous medium:
$\hskip 1pt\dot{\hskip -2.4pt{\cal W}}$
, of the internal (Cauchy) stresses in a continuous medium:
In our case and with the assumption that the density profile is uniform, the strain rate has only one non-zero component, given by
![]() $D_{zz} = \partial _z w = 2\bar {w}/h$
; the stress tensor has the corresponding component σ
zz
(z, t) = − N(z, t). A straightforward calculation of
$D_{zz} = \partial _z w = 2\bar {w}/h$
; the stress tensor has the corresponding component σ
zz
(z, t) = − N(z, t). A straightforward calculation of
![]() $ \hskip 0.9pt\dot{\hskip -0.9pt W}$
using Eqn (15) then yields
$ \hskip 0.9pt\dot{\hskip -0.9pt W}$
using Eqn (15) then yields
Comparison with Eqn (16) immediately shows
![]() $ \hskip 0.9pt\dot{\hskip -0.9pt W} = {\rm D}_t[({\bar {\cal K}} + R_V) h]$
, as it should be.
$ \hskip 0.9pt\dot{\hskip -0.9pt W} = {\rm D}_t[({\bar {\cal K}} + R_V) h]$
, as it should be.
Now, if D t (N (b) h) indeed is the work rate of pressure, directly evaluating it must give the same result as in Eqn (18). From Eqn (15) and the assumed uniform density profile, we obtain
The right-hand sides of Eqns (18) and (19) differ significantly. Equation (18) is derived directly from the principles of continuum mechanics, with the only additional assumption of w(z, t) being linear in z. Equation (19) follows from the postulate (VI.26) combined with the definition (VI.3), the balance Eqn (VI.8), the postulate (VI.12) and assumed linearity of w(z, t). This leaves two alternatives: either D t (N (b) h) is not a correct expression for the depth-integrated work rate of the pressure, or Eqn (VI.21) must be considered an implicit constitutive assumption for the granular pressure. The first alternative has far-reaching consequences: (VI.21) must be abandoned and the basis for the mathematical development in the rest of Sections 5 and 6 of [VI] is invalidated. Instead, one has to adopt Eqn (18) and state a suitable constitutive equation for the granular pressure as a function of the flow variables, e.g., N = N(R K ).
Now consider the second alternative: in this case, D
t
(N
(b)
h) is not the total work rate of the granular pressure. In order for D
t
(N
(b)
h) to be equal to D
t
(R
V
h), the equation
![]() ${\rm D}_t(N^{(b)}h) = {\dot W} \,-\, {\rm D}_t({\bar {\cal K}}h)$
must hold. In the case of linear w(z, t) with h ≡ 2k and
${\rm D}_t(N^{(b)}h) = {\dot W} \,-\, {\rm D}_t({\bar {\cal K}}h)$
must hold. In the case of linear w(z, t) with h ≡ 2k and
![]() $\bar {w} \equiv {\dot k}$
, this leads to
$\bar {w} \equiv {\dot k}$
, this leads to
If m and gz are constant along the avalanche path, then we can perform the time integration (more precisely, the integration along the characteristic line of the control volume) easily and obtain
If the avalanche is at rest (and its depth is 2k 0), N (b) must equal the weight, thus cst. = − (1/2)mgz . However, this leaves no room for a dynamical evolution of the flow depth, and we conclude that the second alternative is not viable.
In our opinion, the most immediate solution of this dilemma in the energy formalism is to explicitly state a constitutive equation for N (b), to express the work rate of the granular pressure in terms of N (b) as
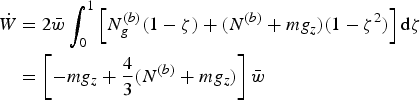 $$\eqalign{ \hskip 0.9pt\dot{\hskip -2pt W} &= 2{\bar w} \int_0^1 \left[N_g^{\lpar b\rpar } \lpar 1-\zeta\rpar + \lpar N^{\lpar b\rpar } + m g_z\rpar \lpar 1-\zeta^2\rpar \right]{\rm d}\zeta \cr &= \left[-m g_z + {4\over 3} \lpar N^{\lpar b\rpar } + m g_z\rpar \right]{\bar w} }$$
$$\eqalign{ \hskip 0.9pt\dot{\hskip -2pt W} &= 2{\bar w} \int_0^1 \left[N_g^{\lpar b\rpar } \lpar 1-\zeta\rpar + \lpar N^{\lpar b\rpar } + m g_z\rpar \lpar 1-\zeta^2\rpar \right]{\rm d}\zeta \cr &= \left[-m g_z + {4\over 3} \lpar N^{\lpar b\rpar } + m g_z\rpar \right]{\bar w} }$$
and to set it equal to the rate of change of kinetic and configuration energy. Using Eqn (16), dividing by
![]() $\bar {w}$
and rearranging terms, we arrive at
$\bar {w}$
and rearranging terms, we arrive at
Not surprisingly, this is the same as Eqn (12) if one makes the constitutive assumption N (b) = γR K . We note that such modification of the extended RKE model also requires modifying the RKE balance equation to properly account for the conversion of RKE to kinetic and configuration energy:
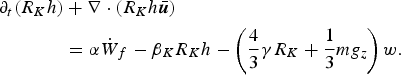 $$\eqalign{\partial_t\lpar R_K h\rpar & + {\bf \nabla} \cdot \lpar R_K h \hskip 0.9pt{\bar{\hskip -0.9pt{\bi u}}} \rpar \cr &= \alpha \hskip 0.9pt\dot{\hskip -0.9pt W}_f - \beta_K R_K h - \left({4\over 3}\gamma R_K + {1\over 3}m g_z\right)w.}$$
$$\eqalign{\partial_t\lpar R_K h\rpar & + {\bf \nabla} \cdot \lpar R_K h \hskip 0.9pt{\bar{\hskip -0.9pt{\bi u}}} \rpar \cr &= \alpha \hskip 0.9pt\dot{\hskip -0.9pt W}_f - \beta_K R_K h - \left({4\over 3}\gamma R_K + {1\over 3}m g_z\right)w.}$$
This will be discussed further when comparing the extended RKE model with the general form of the balance equations for mass, momentum and RKE in Appendix B.
3.4. First-order equation for the flow depth implied by the model assumptions
Our fifth remark is that the modelling assumptions put forth in the text of [VI] together with the energy partitioning postulate (VI.12) imply a simple, first-order evolution equation for h. As the cited text from [VI] states, Eqn (VI.21) is to describe the (advected) rate of change of CED,
![]() ${\rm D}_t R_V \equiv \partial _t R_V +\hskip 0.9pt {\bar {\hskip -0.9pt{\bi u}}}\,\cdot \,{\bf \nabla} R_V$
. Its right-hand side is the production rate of CED, P
V
, integrated over the flow depth. Buser and Bartelt postulate the following equations:
${\rm D}_t R_V \equiv \partial _t R_V +\hskip 0.9pt {\bar {\hskip -0.9pt{\bi u}}}\,\cdot \,{\bf \nabla} R_V$
. Its right-hand side is the production rate of CED, P
V
, integrated over the flow depth. Buser and Bartelt postulate the following equations:
In an avalanche starting at rest, R K (0) = R V (0) = 0. Due to(VI.12), P K = (1 − γ)P so that the advected rates of change of R K and R V are proportional. This immediately leads to
The system of the first four equations defined by (VI.30), (VI.37)–(VI.39), is closed by the assumptions (VI.34)–(VI.36) for
S
b together with Eqn (23) and specified values for α, β
K
and γ. Moreover, throughout [VI] (and [VII]), the authors assume in addition that the density profile is uniform. Then the depth-integrated change rate of the CED can be expressed straightforwardly in terms of
![]() ${\dot h}$
and the mass hold-up: the integral of the potential energy over z relative to the reference configuration is
${\dot h}$
and the mass hold-up: the integral of the potential energy over z relative to the reference configuration is
We will disregard terrain curvature and entrainment for the sake of simplicity. In the Lagrangian point-of-view, D t m = 0. From this, we obtain directly
This first-order differential equation describes relaxation of h to a (quasi-)steady-state value governed by the RKE. This enslavement of R V and h is a direct consequence of the very strong assumption (VI.12). We emphasise that this first-order evolution equation for h is implied by the model assumptions stated in [VI] and that the additional three equations in (VI.30), (VI.37)–(VI.39) at best are superfluous. If one desires a model with more complicated dynamics in the z-direction, one has to replace the assumption (VI.12) by a weaker one that does not enslave R V h.
Closer examination reveals that Eqn (25) does not strictly conserve energy. According to the assumptions made in [VI], part of the frictional work is directly converted to heat, the rest to Rh = (R
K
+ R
V
)h, where R
V
is potential energy and R
K
is fluctuation energy, i.e., 〈w′2〉 = 0 for a suitably defined time or ensemble average 〈.〉. However, if the density changes, D
t
h ≠ 0 and
![]() $\overline {\rho w^2} \gt 0$
, thus there is a contribution from the slope-normal expansion to the total kinetic energy that is not accounted for in the modified model. As mentioned earlier, it might be more natural to include this non-random part of the kinetic energy in the CED; if one does so, energy is conserved. However, Eqn (24) is then no longer valid and a separate evolution equation for the flow depth must be constructed. As explained above, Eqns (VI.5)–(VI.7) are not suitable for this.
$\overline {\rho w^2} \gt 0$
, thus there is a contribution from the slope-normal expansion to the total kinetic energy that is not accounted for in the modified model. As mentioned earlier, it might be more natural to include this non-random part of the kinetic energy in the CED; if one does so, energy is conserved. However, Eqn (24) is then no longer valid and a separate evolution equation for the flow depth must be constructed. As explained above, Eqns (VI.5)–(VI.7) are not suitable for this.
As in the case of the basic RKE model, an analysis of the timescales associated with different processes – in this case, relaxation of the depth-averaged velocity, the RKE, the velocity profile and the density to their steady-state values – is required for a consistent approximation of avalanche flow. We cannot pursue this question further here, but the tight coupling between h,
![]() $\hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}$
and R
K
revealed by Eqn (15), the rapid relaxation of R
K
and our experience from studying alternative snow avalanche models all suggest that algebraic equations for R
K
and h instead of differential ones would produce a simpler, yet more consistent and equally accurate model.
$\hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}$
and R
K
revealed by Eqn (15), the rapid relaxation of R
K
and our experience from studying alternative snow avalanche models all suggest that algebraic equations for R
K
and h instead of differential ones would produce a simpler, yet more consistent and equally accurate model.
3.5. Mathematical formulation of the flow model
A final remark concerns [VI], Section 6, where all model equations are reformulated for implementation in a numerical code. The procedure for doing so is well known and correctly applied for the conserved quantities mass, momentum and RKE in Eqns (VI.30)–(VI.34). Section VI.5 then states that the three first-order evolution Eqns (VI.27)–(VI.29) for k, w and N K (obtained from the erroneous third-order Eqn (VI.17)) are extended to include advection, which indeed is necessary. However, Eqns (VI.37)–(VI.39) present these equations in conservation form, which does not follow from the advected form for non-conserved quantities. For example, the difference between the conservative and advective extensions of (VI.27) is
Clearly, the (2-D) divergence
![]() ${\bf \nabla}\,\cdot \,\bar {{\bi u}}$
does not vanish identically.
${\bf \nabla}\,\cdot \,\bar {{\bi u}}$
does not vanish identically.
4. THE MIXED-AVALANCHE MODEL
4.1. General considerations
The notion of powder-snow avalanche is somewhat fuzzy in the literature. To avoid ambiguity, we will use the term ‘mixed snow avalanche’ (MSA) for flows that simultaneously feature three different flow regimes, namely dense flow (DF), light (or intermediate-density or fluidised) flow (LF) and suspension flow (SF) (see Sovilla and others (Reference Sovilla, McElwaine and Louge2015) for an in depth discussion of these regions). The original RKE-extension of the Voellmy model (Section 2) with constant density is, in principle, applicable only to the DF, but is in practice used to model both the DF and LF regimes. The variable-density model (Section 3) attempts to explicitly model transitions between the DF and LF regimes in a single-layer model. In [VII], the SF regime is added to the model through a second layer.
Based on today's knowledge from observations and measurements, the LF regime may be attained in small avalanches, but is typically more strongly developed in larger avalanches. The SF regime will not be attained unless a considerable part of the avalanche has reached the LF regime. Due to their elevated velocity, parts of the avalanche in the LF regime will reach farther than the parts in the DF regime, and the part in the SF regime may travel yet farther (by several kilometres in extreme cases).
There is probably a smooth transition between flow regimes. This would favour a mathematical description in terms of a multi-phase model (air and snow particles of different sizes), where the density and the stress tensor depend on the volumetric concentrations of the different particle size classes and where air turbulence plays an important role at low particle concentration. However, such a model would have to be formulated as a genuine 3-D model and would at present be poorly suited for practical applications. The different deposit characteristics (Issler and others, Reference Issler, Gauer, Schaer and Keller1996) of the DF and LF regimes as well as some measurements with Frequency-Modulated Continuous-Wave (FMCW) radar suggest that the three flow regimes nevertheless may often be fairly distinct, with large density gradients at their boundaries. This opens the way for models with several layers corresponding to different flow regimes and with depth averaging applied to each layer. Virtually all models proposed so far follow this path. We note in passing that recent detailed measurements in large MSAs at the Vallée de la Sionne test site in Switzerland (Sovilla and others, Reference Sovilla, McElwaine and Louge2015; Köhler and others, Reference Köhler, McElwaine, Sovilla, Ash and Brennan2016) suggest a more complex picture in which sudden, intermittent bursts of rather large and high-density volumes of snow particles play an important role – perhaps not unlike horse-shoe vortices detaching from the bottom surface in turbulent flows. If confirmed, these measurements may question the traditional approach of modelling avalanches in terms of continuum models with slowly varying, depth-averaged fields.
Considered in isolation, the SF is a turbulent suspension of small snow grains in air and a sub-type of particulate gravity currents (Simpson, Reference Simpson1987). The volume concentration of the grains is usually very low (≪0.1) so that grain interactions are not important, though due to the high density of the grains they carry most of the momentum. The excess density of the mixture over the air is referred to as the buoyancy of the current. The density is not constant as on the upper surface ambient air is entrained by turbulence and on the lower surface snow can be lost due to particle settling or gained due to entrainment. All models must therefore have at least three equations for momentum, air mass and snow mass or – equivalently and more commonly – buoyancy and volume. In its initial and final stages, the SF is in the Boussinesq regime where the average density is almost the same as the ambient air density, but it is far in the non-Boussinesq regime when fully developed.
There is a large body of experimental, theoretical and numerical work on density and particulate gravity currents in a variety of idealised settings. It is an important question which of these results remain valid in the case of MSAs and must be taken into account in the modelling of the SF regime. Density and turbidity currents in the laboratory are typically produced from a dilute initial suspension and run over a relatively smooth, non-erodible bed. In contrast, the SF in an MSA forms at the front and on top of the highly agitated LF, and mass is exchanged between the LF and the SF at a high rate. The particle concentration in the SF layer typically being less than 0.01 and the particle settling velocity <1 m s−1, the mechanism of particle suspension inside the layer has to be the same as in other dilute particulate gravity currents and the processes at the upper surface that govern entrainment of ambient air have to follow the general laws observed in high-Reynolds number jet flows, plumes or thermals.
A number of theoretical analyses determine the front velocity of gravity currents by treating them as inviscid, energy-conserving flows without explicitly taking into account turbulence (Benjamin, Reference Benjamin1968; McElwaine, Reference McElwaine2005; Nokes and others, Reference Nokes, Davidson, Stepien, Veale and Oliver2008). The applicability of the results from this approach appears a priori questionable, but recent numerical studies nevertheless appear to confirm it at least for flows without a dense undercurrent (Konopliv and others, Reference Konopliv, Llewellyn Smith, McElwaine and Meiburg2016). In all these situations, one finds that the bed shear stress is negligible compared with the effect of ambient-fluid entrainment along the upper surface. It remains to be seen, however, whether this also holds true in MSAs, where there presumably is a pronounced vertical density gradient across the depth of the SF layer and where the surface of the DF/LF layer beneath can be strongly agitated. Both these flow properties increase the shear stress at the lower interface of the SF layer.
4.2. Basic modelling assumptions in [VII]
The approach proposed in [VII] is a two-layer formulation: a lower layer of intermediate to high (variable) density, consisting of large snow balls, fine snow grains and air for the DF and LF regimes, and an upper layer of low (variable) density containing air and fine snow grains in the SF regime. The air in the SF layer is treated as incompressible and the layer depth and mass per unit footprint area are used instead of air and snow mass. The relative motion between snow grains and air is neglected so that a single momentum balance equation is sufficient for the SF layer. Perhaps surprisingly, the balance of turbulent energy is not considered here, even though the concept of RKE is borrowed from the theory of turbulence, and turbulence is instrumental in maintaining the snow grains in suspension (Parker and others, Reference Parker, Fukushima and Pantin1986; Fukushima and Parker, Reference Fukushima and Parker1990).
We need not discuss the left-hand sides of the balance equations further because they have standard form. Paper [VII] postulates the following source terms for the conservation equations for mass, x− and y-momenta and volume of the suspension layer:
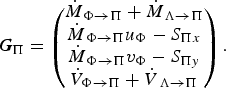 $$ {\bi G}_\Pi = \left(\!\matrix{\hskip 0.9pt\dot{\hskip -0.9pt M}_{\Phi \rightarrow \Pi} + \hskip 0.9pt\dot{\hskip -0.9pt M}_{\Lambda \rightarrow \Pi} \cr \hskip 0.9pt\dot{\hskip -0.9pt M}_{\Phi \rightarrow \Pi} u_\Phi - S_{\Pi x} \cr \hskip 0.9pt\dot{\hskip -0.9pt M}_{\Phi \rightarrow \Pi} v_\Phi - S_{\Pi y} \cr {\dot V}_{\Phi \rightarrow \Pi} + \hskip 0.9pt\dot{\hskip -0.9pt V}_{\Lambda \rightarrow \Pi} }\!\right). $$
$$ {\bi G}_\Pi = \left(\!\matrix{\hskip 0.9pt\dot{\hskip -0.9pt M}_{\Phi \rightarrow \Pi} + \hskip 0.9pt\dot{\hskip -0.9pt M}_{\Lambda \rightarrow \Pi} \cr \hskip 0.9pt\dot{\hskip -0.9pt M}_{\Phi \rightarrow \Pi} u_\Phi - S_{\Pi x} \cr \hskip 0.9pt\dot{\hskip -0.9pt M}_{\Phi \rightarrow \Pi} v_\Phi - S_{\Pi y} \cr {\dot V}_{\Phi \rightarrow \Pi} + \hskip 0.9pt\dot{\hskip -0.9pt V}_{\Lambda \rightarrow \Pi} }\!\right). $$
![]() $\dot{\hskip -0.9pt V}_{\Phi \rightarrow \Pi }$
and
$\dot{\hskip -0.9pt V}_{\Phi \rightarrow \Pi }$
and
![]() $\dot{\hskip -0.9pt V}_{\Lambda \rightarrow \Pi }$
are the volume fluxes from the dense core (Φ) and the ambient air (Λ) to the suspension layer (Π), and
$\dot{\hskip -0.9pt V}_{\Lambda \rightarrow \Pi }$
are the volume fluxes from the dense core (Φ) and the ambient air (Λ) to the suspension layer (Π), and
![]() ${\hskip .5pt \dot{\hskip -0pt M}}_{\Phi \rightarrow \Pi }$
and
${\hskip .5pt \dot{\hskip -0pt M}}_{\Phi \rightarrow \Pi }$
and
![]() $\dot{\hskip -0.9pt M}_{\Lambda \rightarrow \Pi }$
are the associated mass fluxes.
S
Π denotes the surficial shear stress on the suspension layer. In what follows, we will change the notation from
$\dot{\hskip -0.9pt M}_{\Lambda \rightarrow \Pi }$
are the associated mass fluxes.
S
Π denotes the surficial shear stress on the suspension layer. In what follows, we will change the notation from
![]() $\dot{\hskip -0.9pt M}_{\Phi \rightarrow \Pi }$
,
$\dot{\hskip -0.9pt M}_{\Phi \rightarrow \Pi }$
,
![]() $\hskip 0.9pt\dot{\hskip -0.9pt M}_{\Lambda \rightarrow \Pi }$
,
$\hskip 0.9pt\dot{\hskip -0.9pt M}_{\Lambda \rightarrow \Pi }$
,
![]() $\hskip 3pt \dot{\hskip -0.9pt V}_{\Phi \rightarrow \Pi }$
,
$\hskip 3pt \dot{\hskip -0.9pt V}_{\Phi \rightarrow \Pi }$
,
![]() $\dot{\hskip -0.9pt V}_{\Lambda \rightarrow \Pi }$
to
$\dot{\hskip -0.9pt V}_{\Lambda \rightarrow \Pi }$
to
![]() $Q_{\Phi \rightarrow \Pi }$
,
$Q_{\Phi \rightarrow \Pi }$
,
![]() $Q_{\Lambda \rightarrow \Pi }$
,
$Q_{\Lambda \rightarrow \Pi }$
,
![]() $W_{\Phi \rightarrow \Pi }$
,
$W_{\Phi \rightarrow \Pi }$
,
![]() $W_{\Lambda \rightarrow \Pi }$
because these quantities are not advective derivatives of M
Φ, M
Π, h
Φ and h
Π, as the dot notation would imply.
$W_{\Lambda \rightarrow \Pi }$
because these quantities are not advective derivatives of M
Φ, M
Π, h
Φ and h
Π, as the dot notation would imply.
4.3. The role of gravity
A particular feature of the MSA model of [VII] – immediately apparent from the second and third components of G Π in (VII.35) – is that gravity is neglected in the dynamics of the SF layer, both as the driving force and as the cause of sedimentation. This is different to every other model of gravity currents and contradicts a large body of well-documented research showing that gravity and air entrainment at the top surface are the dominant terms in the momentum balance of density currents (Hopfinger, Reference Hopfinger1983; Meiburg and others, Reference Meiburg, McElwaine, Kneller and Fernando2012). Such an approximation might be justified when describing the motion of jets of almost particle-free air ejected from the avalanche, but this would be devoid of practical relevance. Neglecting sedimentation is less grave unless one is interested in the late run-out phase of the PSA, where the flow rarely does damage.
The missing processes are easily introduced into the source term (VII.35):
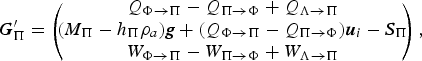 $$ {\bi G}_\Pi' = \left(\!\!\! \matrix{ Q_{\Phi\rightarrow\Pi} - Q_{\Pi\rightarrow\Phi} + Q_{\Lambda\rightarrow\Pi} \cr \lpar M_\Pi-h_\Pi\rho_a\rpar {\bi g} + \lpar Q_{\Phi\rightarrow\Pi}-Q_{\Pi\rightarrow\Phi}\rpar {\bi u}_i - {\bi S}_\Pi \cr W_{\Phi\rightarrow\Pi} - W_{\Pi\rightarrow\Phi} + W_{\Lambda\rightarrow\Pi} }\!\!\! \right)\comma $$
$$ {\bi G}_\Pi' = \left(\!\!\! \matrix{ Q_{\Phi\rightarrow\Pi} - Q_{\Pi\rightarrow\Phi} + Q_{\Lambda\rightarrow\Pi} \cr \lpar M_\Pi-h_\Pi\rho_a\rpar {\bi g} + \lpar Q_{\Phi\rightarrow\Pi}-Q_{\Pi\rightarrow\Phi}\rpar {\bi u}_i - {\bi S}_\Pi \cr W_{\Phi\rightarrow\Pi} - W_{\Pi\rightarrow\Phi} + W_{\Lambda\rightarrow\Pi} }\!\!\! \right)\comma $$
where ρ
a
is the density of the ambient air. The buoyancy term (the left-most term in the middle row of Eqn (26)) is present in all earlier PSA models we are aware of. The grain-borne shear stress (middle term in the second row) represents the momentum flux from one layer to the other due to the mass flux. It is the product of the net entrainment rate (entrainment minus sedimentation) and the (slope-parallel) velocity at the interface,
u
i
. The latter needs to be modelled as a function of
![]() $\bar {{\bi u}}_\Phi $
,
$\bar {{\bi u}}_\Phi $
,
![]() $\bar {{\bi u}}_\Pi $
and the densities in the two layers, but we will not go further into this question. The relation between mass and volume loss of the PSA cloud due to settling of snow grains is
$\bar {{\bi u}}_\Pi $
and the densities in the two layers, but we will not go further into this question. The relation between mass and volume loss of the PSA cloud due to settling of snow grains is
![]() $Q_{\Pi \rightarrow \Phi } = \rho _i W_{\Pi \rightarrow \Phi }$
, assuming that all particles in the PSA cloud are snow grains with the density of ice, ρ
i. A candidate model for the sedimentation rate is the one used by Parker and others (Reference Parker, Fukushima and Pantin1986),
$Q_{\Pi \rightarrow \Phi } = \rho _i W_{\Pi \rightarrow \Phi }$
, assuming that all particles in the PSA cloud are snow grains with the density of ice, ρ
i. A candidate model for the sedimentation rate is the one used by Parker and others (Reference Parker, Fukushima and Pantin1986),
where M Π/h Π is the depth-averaged PSA density, w s the average settling velocity of the snow particles, and θ the local slope angle. c b, the ratio of bottom snow concentration to depth-averaged concentration, needs to be assumed, the most plausible values being in the range 3–10.
4.4. Air entrainment and drag on the suspension layer
Paper [VII] does not specify the air entrainment rate
![]() $Q_{\Lambda \rightarrow \Pi }$
appearing in (VII.35) and in the first row of Eqn (26). This entrainment rate has been measured repeatedly in inclined plumes and particulate gravity currents since the pioneering experiments by Ellison and Turner (Reference Ellison and Turner1959). It is well understood by now that it is governed by the Richardson number (Turner, Reference Turner1973). (Turnbull and others (Reference Turnbull, McElwaine and Ancey2007) provide a summary of these ideas applied to avalanches.) The Richardson number is the ratio of the potential energy to the kinetic energy of a parcel of fluid. For an entire layer, one defines the bulk Richardson number,
$Q_{\Lambda \rightarrow \Pi }$
appearing in (VII.35) and in the first row of Eqn (26). This entrainment rate has been measured repeatedly in inclined plumes and particulate gravity currents since the pioneering experiments by Ellison and Turner (Reference Ellison and Turner1959). It is well understood by now that it is governed by the Richardson number (Turner, Reference Turner1973). (Turnbull and others (Reference Turnbull, McElwaine and Ancey2007) provide a summary of these ideas applied to avalanches.) The Richardson number is the ratio of the potential energy to the kinetic energy of a parcel of fluid. For an entire layer, one defines the bulk Richardson number,
where θ is the angle between the slope normal and vertical. This implies that the entrainment rate depends both on the slope inclination, as shown experimentally, e.g., by Ellison and Turner (Reference Ellison and Turner1959) and Beghin and Olagne (Reference Beghin and Olagne1991), and on the density difference.
Based on laboratory experiments, Turner (Reference Turner1986) proposed the following formula for the entrainment coefficient:
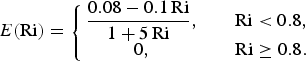 $$ E\lpar {\rm Ri}\rpar = \left\{\matrix{{} \displaystyle {0.08 - 0.1\, {\rm Ri}\over 1 + 5\, {\rm Ri}} \comma & \quad {\rm Ri} \lt 0.8 \comma \cr 0\comma & \quad {\rm Ri} \geq 0.8.} \right. $$
$$ E\lpar {\rm Ri}\rpar = \left\{\matrix{{} \displaystyle {0.08 - 0.1\, {\rm Ri}\over 1 + 5\, {\rm Ri}} \comma & \quad {\rm Ri} \lt 0.8 \comma \cr 0\comma & \quad {\rm Ri} \geq 0.8.} \right. $$
Ancey (Reference Ancey2004) more recently fitted unpublished data of Beghin by the function
where λ = 1.6. This provides an even better closure for the volume and air-mass balances
Bartelt and co-workers assume the sum of the shear stresses on the upper and lower interfaces of the SF layer to be proportional to the square of the cloud velocity, u Π 2, and the cloud density, ρ Π, writing
The drag coefficient ξ Π is considered a constant to be selected by the user. The authors state that the dominant contribution to the drag is from air entrainment at the upper boundary.
There are two issues with these assumptions: (i) If indeed air entrainment is the dominant contribution to the retarding forces on the SF layer, S Π ≈ 0 would result because entrainment of ambient air at rest does not remove momentum from the SF layer, but distributes it over an increasing mass and thus decelerates the flow. To see this, multiply the mass-balance equation
by
![]() $\bar {{\hskip -0.9pt{\bi u}}}$
and subtract it from the momentum-balance equation
$\bar {{\hskip -0.9pt{\bi u}}}$
and subtract it from the momentum-balance equation
This produces the equation of motion
which correctly features the decelerating force due to the acceleration of the ingested mass if this mass originally is at rest. (ii) Drag at the lower boundary should depend, not on the SF layer velocity, but on the difference between SF layer and DF/LF layer velocities. It is thus seen that the model presented in [VII] effectively assumes the interfacial shear stress between the DF/LF layer and the SF layer to be given by Eqn (VII.37), whereas the entrainment function
![]() $W_{\Lambda \rightarrow \Pi }$
is not specified in the paper. Replacing
$W_{\Lambda \rightarrow \Pi }$
is not specified in the paper. Replacing
![]() $\bar {{\bi u}}_\Pi ^2$
by
$\bar {{\bi u}}_\Pi ^2$
by
![]() $(\bar {{\bi u}}_\Pi \,-\, \bar {{\bi u}}_\Phi )^2$
in (VII.37) and specifying
$(\bar {{\bi u}}_\Pi \,-\, \bar {{\bi u}}_\Phi )^2$
in (VII.37) and specifying
![]() $W_{\Lambda \rightarrow \Pi }$
and
$W_{\Lambda \rightarrow \Pi }$
and
![]() $Q_{\Lambda \rightarrow \Pi }$
according to Eqn (31) with either (29) of (30) would then provide a physically consistent, but rather crude closure, provided the opposite term +
S
Π is added to the momentum-balance equation of the DF/LF layer: the modified Eqn (VII.37) does not take into account that the interfacial shear stress will depend strongly on the densities in both layers.
$Q_{\Lambda \rightarrow \Pi }$
according to Eqn (31) with either (29) of (30) would then provide a physically consistent, but rather crude closure, provided the opposite term +
S
Π is added to the momentum-balance equation of the DF/LF layer: the modified Eqn (VII.37) does not take into account that the interfacial shear stress will depend strongly on the densities in both layers.
The authors correctly note that air entrainment at the upper interface is the main source of resistance for the powder-snow cloud. However, there are also pressure forces acting, though the distinction between pressure drag and turbulent entrainment is not as straightforward as it first appears. For pressure to have a net retarding force there must be a separation region behind an object and a turbulent wake, otherwise we have D'Alembert's paradox that there is no drag. Thus, the momentum transfer from the pressure drag goes into a momentum deficit in the turbulent wake. This turbulent mixing region contains snow and if we regard it as part of the SF layer, then correctly accounting for the momentum balance here means that we do not need to directly consider the pressure drag. A more detailed discussion and quantitative analysis from a direct numerical simulation is contained in (Konopliv and others, Reference Konopliv, Llewellyn Smith, McElwaine and Meiburg2016).
This is correct if we consider the momentum balance over a large region containing the front, but if we wish for a more detailed model this can be improved. The pressure distribution along the SF layer surface is obtained by solving an elliptic potential flow problem in the ambient fluid. At the nose of the avalanche there will be a positive (with respect to the background pressure) stagnation pressure, but moving back along the top surface the pressure decreases linearly and may become negative (McElwaine, Reference McElwaine2005). Perhaps the best method would be to solve this potential flow problem using a boundary element method (Nokes and others, Reference Nokes, Davidson, Stepien, Veale and Oliver2008). This approach has not yet been directly applied to geophysical flows (see (De Blasio and others, Reference De Blasio2004) for a simplistic approximation). In addition, the shallowness approximation is violated since the front angle will be approximately 60 degrees (McElwaine, Reference McElwaine2005). Instead, the more usual approach is to apply a front condition by imposing a constant Froude number, thus setting the front velocity as a function of the front height.
In addition, added-mass effects (which give additional drag when an avalanche is accelerating) may also be relevant for powder-snow clouds of low density (Turnbull and others, Reference Turnbull, McElwaine and Ancey2007).
4.5. Formation of the suspension layer
The authors of [VII] interpret the cleft-and-lobe structure of MSA fronts as firm evidence for what they term blow-out. This proposed mechanism for SF layer formation can be summarised as a consequence of a hypothetical ‘breather’ mode in the motion of the dense core: the latter would expand periodically (normal to the slope) due to dispersive pressure and then contract again. During the expansion, air would be ingested and mixed with fine snow dust; when the large particles fall down again, the nascent powder-snow cloud would be expelled from the core as plumes (or rather puffs in conventional terminology), forming the observed lobes and clefts.
Paper [VII] specifies the boundary fluxes for the suspension layer as (in our notation)
where the Heaviside distribution Θ(x) is 1 for x < 0 and 0 otherwise. Precisely speaking, (VII.24) and (VII.25) refer to the avalanche core, and as such (VII.24) is merely a kinematic statement. Together they describe the first half of one cycle in the ‘breather’ mode that is invoked here. The second half of the cycle transfers mass and momentum from the core to the SF layer and is described by (VII.26) and (VII.27).
As stated above and by (VII.24), the core entrains air (without ice dust) at the rate
![]() $W_{\Lambda \rightarrow \Phi }$
. In contrast, (VII.25) states that the core entrains mass from the ambient air at the rate
$W_{\Lambda \rightarrow \Phi }$
. In contrast, (VII.25) states that the core entrains mass from the ambient air at the rate
![]() $Q_{\Lambda \rightarrow \Phi } = \rho _{\Pi _0} W_{\Lambda \rightarrow \Phi }$
, i.e., air laden with ice dust. This is likely a typographical error, and ρ
Π0
should be replaced by ρ
a. Even so,
$Q_{\Lambda \rightarrow \Phi } = \rho _{\Pi _0} W_{\Lambda \rightarrow \Phi }$
, i.e., air laden with ice dust. This is likely a typographical error, and ρ
Π0
should be replaced by ρ
a. Even so,
![]() $Q_{\Lambda \rightarrow \Phi }$
does not appear in (VII.34) and (VII.35), while the terms
$Q_{\Lambda \rightarrow \Phi }$
does not appear in (VII.34) and (VII.35), while the terms
![]() $W_{\Lambda \rightarrow \Pi }$
and
$W_{\Lambda \rightarrow \Pi }$
and
![]() $Q_{\Lambda \rightarrow \Pi }$
appearing in (VII.35) are not explicitly defined in [VII]. Thus, the first, second, third and fifth components in Eqn (VII.34) should be amended to read
$Q_{\Lambda \rightarrow \Pi }$
appearing in (VII.35) are not explicitly defined in [VII]. Thus, the first, second, third and fifth components in Eqn (VII.34) should be amended to read
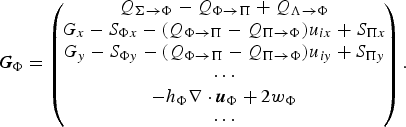 $$ {\bi G}_\Phi = \left(\!\! \matrix{ Q_{\Sigma\rightarrow\Phi} - Q_{\Phi\rightarrow\Pi} + Q_{\Lambda\rightarrow\Phi} \cr G_x - S_{\Phi x} - \lpar Q_{\Phi\rightarrow\Pi} - Q_{\Pi\rightarrow\Phi}\rpar u_{ix} + S_{\Pi x} \cr G_y - S_{\Phi y} - \lpar Q_{\Phi\rightarrow\Pi} - Q_{\Pi\rightarrow\Phi}\rpar u_{iy} + S_{\Pi y} \cr \cdots \cr - h_\Phi {\bf \nabla}\cdot{\bi u}_\Phi + 2 w_\Phi \cr \cdots }\!\! \right). $$
$$ {\bi G}_\Phi = \left(\!\! \matrix{ Q_{\Sigma\rightarrow\Phi} - Q_{\Phi\rightarrow\Pi} + Q_{\Lambda\rightarrow\Phi} \cr G_x - S_{\Phi x} - \lpar Q_{\Phi\rightarrow\Pi} - Q_{\Pi\rightarrow\Phi}\rpar u_{ix} + S_{\Pi x} \cr G_y - S_{\Phi y} - \lpar Q_{\Phi\rightarrow\Pi} - Q_{\Pi\rightarrow\Phi}\rpar u_{iy} + S_{\Pi y} \cr \cdots \cr - h_\Phi {\bf \nabla}\cdot{\bi u}_\Phi + 2 w_\Phi \cr \cdots }\!\! \right). $$
The first term of the fifth component corrects for the conservation form of the left-hand side of the balance Eqn (VII.28); see Section 3 for further necessary modifications of (VII.32) and (VII.34).
Besides these technical issues, the proposed SF formation mechanism presents two conceptual problems. First, lobes and clefts cannot be considered evidence for this mechanism. They form inevitably as instabilities in all types of highly turbulent gravity flows, with or without suspended particles, on completely flat and smooth surfaces (Simpson, Reference Simpson1987). Even if there is no dense underflow and the proposed ‘blow-out’ mechanism cannot be operative, the same type of structure is observed. Engulfing of ambient air by large eddies (similar in size to the flow depth) is the main entrainment mechanism in turbulent gravity currents and may indeed lead to the impression that dense jets are ejected from the flow. In MSAs, the density gradients are expected to be large except in the late stage; this will accentuate the impression of jets shooting out. To make their proposal more than speculation, the authors ought to show that the conventional mechanisms fail to reproduce central aspects of MSA behaviour or, ideally, perform measurements at the interface of the core and the suspension layer.
Another crucial aspect of the ‘blow-out’ mechanism is not addressed in [VI] or [VII], but in [V]: the core must undergo some kind of intermittency or oscillatory behaviour with a rather large amplitude to eject large volumes of snow–air mixture. Such behaviour indeed arose in the model described in [V] since the second-order equation for the vertical velocity derived in that paper has no damping term. However, as we show in Section 3, that equation lacks a proper physical basis.
Finally, we note that the ‘blow-out’ mechanism as described in [VII] requires that there is no suspension layer above the core during the first (expansion) half of the cycle; otherwise, the core could not entrain ‘pure’ ambient air, as is stated before (VII.24) and (VII.25). This means that the puff of snow–air mixture that is ejected during core contraction must immediately move away from the core segment that ejected it before the next expansion begins. This may work for the front, but core segments behind the nose will typically have a puff above them when they expand, and thus ‘swallow’ the suspension layer rather than ingesting ambient air. There is no indication in [VII] of how the model prevents the core from repeatedly incorporating what it has just expelled.
5. CONCLUDING REMARKS
There can be little doubt that the general thrust of the work described in [I]–[VII] is promising and will lead to more realistic avalanche models over time. However, the preceding sections revealed that the models in their present form have shortcomings both in their physical foundations and their mathematical formulation that need to be dealt with. Our main findings can be summarised as follows:
-
1. In sharp contrast with all other models in practical use today, the effective friction coefficient of the RKE-extended Voellmy model decreases with speed rather than increasing (provided the RKE is reasonably close to its equilibrium value). This friction law should therefore be regarded as heuristic, and its predictions should be compared with detailed measurements and, e.g., the Jenkins–Askari model. It will not be suitable as the foundation of a comprehensive, physics-based theoretical model unless one can show it to be a controlled approximation to a more physical model.
-
2. Inclusion of density changes adds a considerable amount of complexity to an avalanche model. Papers [V]–[VII] attempt to circumvent some of it by adopting an energy-based approach rather than a momentum-balance equation in the z-direction. For closure, [VI] and [VII] assume that the energy supply to the configuration energy density (CED) is a fixed fraction of the net production rate of the sum of CED and RKE. A critical issue is the expression for the work rate of pressure, with D t (Nh) used instead of ½
 $ N_g {\rm D}_t h$
in Eqn (VI.21). This leads to a spurious third-order equation for the flow depth in [V]–[VII], in lieu of the first-order evolution equation that results if the stated framework is applied correctly. Additionally it is inconsistent to model such a rapid process by an evolution equation when an anelastic type algebraic closure is much more suitable.
$ N_g {\rm D}_t h$
in Eqn (VI.21). This leads to a spurious third-order equation for the flow depth in [V]–[VII], in lieu of the first-order evolution equation that results if the stated framework is applied correctly. Additionally it is inconsistent to model such a rapid process by an evolution equation when an anelastic type algebraic closure is much more suitable. -
3. If one abandons the simplistic assumption for the energy supply rate to the CED, a more realistic description of the variable-density system becomes possible. We conjecture that a physically consistent and realistic, yet relatively simple model results if one assumes a linear relation between RKE and total bottom pressure. Additionally, the RKE balance equation must be extended to account for the two-way coupling between RKE and CED. This system and possibly additional options need to be studied further in order to find a physically sound and practical model.
-
4. The balance equations of the SF layer in [VII] are in contradiction to all other models and firmly established experimental results on dilute gravity mass flows. The source terms should include gravity, particle settling/entrainment and entrainment of ambient air. The important questions, which are as yet unclear or controversial, are the following: Which parameterisation of the entrainment rate as a function of the Richardson number is most appropriate? What is the form of the density profile? What is the form of the velocity profile? Is there a significant interfacial shear stress between the DF/LF layer and the SF layer other than the momentum flux associated with mass exchange?
-
5. The proposed mechanism for generating a PSA from a dense avalanche is novel, but highly speculative. It depends on a ‘breather mode’ being excited in the dense flow, for which evidence is at best inconclusive. There is need for further work comparing the mechanism proposed in [VII] to more conventional alternatives.
We expect that the necessary changes can be incorporated in the model without major difficulties and that they will simplify the equations for the density-changing DF/LF layer considerably. There is a wide spectrum of alternative formulations, in particular with regard to the DF rheology and the generation mechanism for the SF layer, that are worth exploring. In particular, the early work [I,II] on fitting velocity profiles measured in full-scale experiments holds promise of finding a consistent and experimentally verified rheology to replace the heuristic RKE-modified Voellmy friction law.
ACKNOWLEDGMENTS
Reviewing this paper required an extraordinary amount of effort as it effectively amounted to reviewing papers [I]–[VII] as well. We express our sincere gratitude to C. Ancey and an anonymous referee for their insightful and constructive reviews and to N. Eckert, S. H. Faria and J. C. Cogley for their editorial advice. We are grateful for the hospitality of the Max Planck Institute for the Physics of Complex Systems in Dresden, Germany, where work on this paper started during the geoflow16 workshop. DI acknowledges correspondence from Perry Bartelt that clarified some questions related to paper [VI]. Part of DI's work was funded by the grant for snow avalanche research from the Norwegian Department of Oil and Energy, administrated by the Norwegian Water Resources and Energy Directorate. JJ acknowledges travel support associated with his visit to the Max Planck Program geoflow16 received from US NSF award 1619768 to Cornell University.
APPENDIX A. FURTHER REMARKS ON THE RKE MODEL
Papers [I], [II] and [VI] invoke a number of concepts that look plausible and innocuous at first, but warrant a more detailed discussion. In this appendix, we collect issues that do not directly affect the model equations.
A.1 Viscous shear vs inelastic collisions
Bartelt and Buser distinguish between viscous shear work and inelastic collisions associated with RKE. The first notion stems from a macroscopic description of the granular material, while the second notion corresponds to a microscopic viewpoint. The kinetic theory of granular materials shows in a precise mathematical way how particle collisions give rise to a close analogue of viscosity in fluids (Jenkins and Savage, Reference Jenkins and Savage1983). As in the theory of turbulence, correlations of fluctuation velocities create a contribution to the stress tensor in a granular assembly. This implies that one cannot separate these notions from one another, as is done in [I] and [II].
A.2 Work done by random particle motion
Equations (I.5) and (I.6) stipulate that the forces arising from the random motion of particles average to zero because of their randomness and thus RKE cannot be converted to kinetic or potential energy. In papers [V]–[VII], this statement is tacitly revoked and γR K is effectively used as the dispersive pressure. But where precisely lies the flaw in the argument of [I]? One can trace the problem to the stipulation that random motion produces random forces that average to zero. However, forces are exerted by one system on another. If system A is a granular assembly and we disregard static electricity, A can exert a force on some other system B only if A and B are in contact with each other. System B would typically be a container wall, creating a boundary for the granular assembly. This causes an asymmetry: particles approaching the right-hand side wall have a wall-normal velocity component v ⊥ > 0, but after the collision, v′⊥ < 0. The force on the wall depends, not on the average of v ⊥ and v′⊥, but on v ⊥ − v′⊥, which necessarily is larger than 0 due to the presence of the boundary. If the particle collisions with the wall are strong and frequent enough, they will push the container wall outward and do mechanical work.
A.3 Energy balances
The energy balance (I.19) (or its equivalent forms (I.7) and (I.11)) looks deceptively simple and straightforward:
However, [I] emphasises that
![]() $\dot {W}_f$
is always negative because the friction force opposes the direction of motion. Subtracting a negative work rate from the avalanche energy would therefore increase that energy, thus the sign of this term must be changed. We will henceforth consider the equation with corrected sign. To emphasise the conservative character of the gravitational force in contrast to the dissipative nature of friction, we will apply (I.9),
$\dot {W}_f$
is always negative because the friction force opposes the direction of motion. Subtracting a negative work rate from the avalanche energy would therefore increase that energy, thus the sign of this term must be changed. We will henceforth consider the equation with corrected sign. To emphasise the conservative character of the gravitational force in contrast to the dissipative nature of friction, we will apply (I.9),
![]() $ \hskip 0.9pt \dot{\hskip -2pt U} = - \hskip 0.9pt \dot{\hskip -0.9pt W}_g$
, in reverse and use the gravitational potential energy instead of the gravitational work rate. We thus discuss the equation
$ \hskip 0.9pt \dot{\hskip -2pt U} = - \hskip 0.9pt \dot{\hskip -0.9pt W}_g$
, in reverse and use the gravitational potential energy instead of the gravitational work rate. We thus discuss the equation
The authors apply this energy balance in the framework of a depth-averaged flow model. Moreover, the shear is assumed to be concentrated in a very thin bottom layer, i.e., one assumes the velocity profile to be uniform inside the avalanche and the slip velocity to be equal to the (depth-averaged) flow velocity. Let us therefore test (I.19') by considering a block of mass m sliding on a horizontal surface, with friction coefficient μ and initial velocity u 0. The equation of motion is readily integrated:
and gives the kinetic energy
The time-dependent term on the right-hand side exactly equals the work done on the block by the external friction force,
as s(t) = u
0
t − μ
gt
2/2. Thus, we find K(t) = K
0 + W
f
(t). Since there is no gravitational work in this case, this corresponds to (I.19'), but with
![]() $\dot {R} + {\dot \Phi } = 0$
. However, the frictional work surely has been converted into heat (
$\dot {R} + {\dot \Phi } = 0$
. However, the frictional work surely has been converted into heat (
![]() $\dot {\Phi } \gt 0$
), so why does it not show up in the balance equation? The answer is that the heat is not generated inside the sliding block but at the boundary and (I.19') lacks a term describing the heat flux across the boundary of the block. The correct form of Eqn (I.19) would therefore be
$\dot {\Phi } \gt 0$
), so why does it not show up in the balance equation? The answer is that the heat is not generated inside the sliding block but at the boundary and (I.19') lacks a term describing the heat flux across the boundary of the block. The correct form of Eqn (I.19) would therefore be
where Q a is the sum of the granular and thermal heat fluxes into the avalanche, integrated over the control volume surface.
The equation of motion implies
![]() $\dot {K} + \hskip 2pt \dot{\hskip -2pt U} = {\dot W}_f$
; thus we get
$\dot {K} + \hskip 2pt \dot{\hskip -2pt U} = {\dot W}_f$
; thus we get
![]() $ \hskip 0.9pt \dot{\hskip -0.9pt R} + {\dot \Phi } = Q_{{\rm a}}$
, but we do not know the value of Q
a. We can obtain some qualitative insight if we consider an (infinitesimally) thin control volume along the interface, in which all the shear is concentrated. Friction converts kinetic energy of the sliding block into heat and RKE inside the shear layer at a rate
$ \hskip 0.9pt \dot{\hskip -0.9pt R} + {\dot \Phi } = Q_{{\rm a}}$
, but we do not know the value of Q
a. We can obtain some qualitative insight if we consider an (infinitesimally) thin control volume along the interface, in which all the shear is concentrated. Friction converts kinetic energy of the sliding block into heat and RKE inside the shear layer at a rate
![]() $- {\dot W}_f \gt 0$
. With its infinitesimal volume, the shear layer has, however, only a vanishingly small capacity for storing this energy. This means that the total heat and RKE flux out of the shear layer into the avalanche, Q
a
, and the snow cover, Q
s
, must equal
$- {\dot W}_f \gt 0$
. With its infinitesimal volume, the shear layer has, however, only a vanishingly small capacity for storing this energy. This means that the total heat and RKE flux out of the shear layer into the avalanche, Q
a
, and the snow cover, Q
s
, must equal
![]() $- \hskip 0.9pt \dot{\hskip -0.9pt W}_f$
. Clearly, Q
s
> 0 in a snow avalanche so that
$- \hskip 0.9pt \dot{\hskip -0.9pt W}_f$
. Clearly, Q
s
> 0 in a snow avalanche so that
![]() $0 \lt Q_{{\rm a}} \lt - \hskip 0.9pt \dot{\hskip -0.9pt W}_f = \hskip 0.9pt \dot{\hskip -0.9pt R} + {\dot \Phi }$
. Comparing with (I.17),
$0 \lt Q_{{\rm a}} \lt - \hskip 0.9pt \dot{\hskip -0.9pt W}_f = \hskip 0.9pt \dot{\hskip -0.9pt R} + {\dot \Phi }$
. Comparing with (I.17),
one sees that Bartelt and Buser assume Qs ≈ 0,
![]() $ \hskip 0.9pt \dot{\hskip -0.9pt R} = \alpha Q \, -\beta R$
, and
$ \hskip 0.9pt \dot{\hskip -0.9pt R} = \alpha Q \, -\beta R$
, and
![]() $\dot {\Phi } = (1\,-\,\alpha ) Q + \beta R$
. With these assumptions, the balance Eqn (I.19') reduces to
$\dot {\Phi } = (1\,-\,\alpha ) Q + \beta R$
. With these assumptions, the balance Eqn (I.19') reduces to
In contrast, the original Eqn (I.19') (after correcting the sign error) would imply that the snow cover absorbs all the frictional work. The preceding analysis also applies to a flow with internal shear with a few modifications.
In Section 7 of [VI], Buser and Bartelt attempt to show that their equation system conserves energy. To this end, they split the (non-random) kinetic energy into two components, defined as
![]() $K^{xy} \equiv \overline {\rho {\bi u}^2}/2$
and
$K^{xy} \equiv \overline {\rho {\bi u}^2}/2$
and
![]() $K^z \equiv \overline {\rho w^2}/2$
, and state the following balance equations:
$K^z \equiv \overline {\rho w^2}/2$
, and state the following balance equations:
Among multiple issues connected with (VI.41), we mention the following: (i) The kinetic energy balances should be derived directly from the momentum-balance equations. In doing so, Eqn (VI.40) would receive a contribution from the (slope-parallel) gradient of normal stresses, and Eqn (VI.41) would be supplemented by a contribution due to dispersive pressure. (ii) The model is not fully closed in the sense that evaluating
![]() $\dot {W}_f^z = \int _0^h {\bf \nabla}\,\cdot \,{\bi S}(z)\, {\rm d} z$
would require constitutive expressions for the shear stresses
S
(z) across the flow depth. The Voellmy-type bed-friction law provides only the bed shear stress,
S
b
. (iii) Equation (VI.41) should contain either the rate of change of potential energy, D
t
(R
V
h), or the work rate of gravity,
$\dot {W}_f^z = \int _0^h {\bf \nabla}\,\cdot \,{\bi S}(z)\, {\rm d} z$
would require constitutive expressions for the shear stresses
S
(z) across the flow depth. The Voellmy-type bed-friction law provides only the bed shear stress,
S
b
. (iii) Equation (VI.41) should contain either the rate of change of potential energy, D
t
(R
V
h), or the work rate of gravity,
![]() $- \hskip 0.9pt \dot{\hskip -0.9pt W}_g^z$
, but not both. Gravity being a conservative force, the change of potential energy is the opposite of the work done by gravity, thus
$- \hskip 0.9pt \dot{\hskip -0.9pt W}_g^z$
, but not both. Gravity being a conservative force, the change of potential energy is the opposite of the work done by gravity, thus
![]() $ {\rm D}_t(R_V h) = + \hskip 0.9pt \dot{\hskip -0.9pt W}_g^z$
with the sign convention of Eqn (VI.5). When this is taken into account, (VI.41) degenerates to
$ {\rm D}_t(R_V h) = + \hskip 0.9pt \dot{\hskip -0.9pt W}_g^z$
with the sign convention of Eqn (VI.5). When this is taken into account, (VI.41) degenerates to
![]() $\dot {K}_z = \,-\, \hskip 0.9pt \dot{\hskip -0.9pt W}_f^z$
. As mentioned above, this relation lacks the main term, namely the contribution from the dispersive pressure gradient.
$\dot {K}_z = \,-\, \hskip 0.9pt \dot{\hskip -0.9pt W}_f^z$
. As mentioned above, this relation lacks the main term, namely the contribution from the dispersive pressure gradient.
APPENDIX B. COMPARISON WITH THE GENERAL BALANCE EQUATIONS FOR MASS, MOMENTUM AND FLUCTUATION ENERGY
Further insight into the significance of the constitutive assumptions in the density-changing RKE model can be obtained by comparing it with the general depth-averaged balance equations for mass, momentum and fluctuation energy, of which it has to be a special instance if it is to be consistent. For simplicity, consider flow down a straight, rigid incline at an angle θ to the horizontal. We take x in the flow direction, y horizontal in the sliding plane and z normal to the incline, with origin at the base and positive upward, x α = (x, y, z)T, ρ the average mass density of the grains, and u α = (u, v, w)T the components of the ensemble-averaged grain velocity. We will first state the equations for a general 3-D flow and then discard the variations along the x- and y-directions to make the comparison simpler.
From the general principles of fluid mechanics, the mass-balance equation must take the local form
(We use tensor notation here to emphasise that these equations are 3-D and switch to vector notation after depth-averaging. Summation over repeated indices is understood.) Take σ αβ to be the components of particle stress and f α = g(sinθ, 0, − cosθ)T the components of external force per unit mass, with g the gravitational acceleration. Then the local balance of linear momentum is
With
![]() ${\cal K} \equiv (1/2)\rho u_{\alpha} u_{\alpha} $
, the balance of mechanical energy reads
${\cal K} \equiv (1/2)\rho u_{\alpha} u_{\alpha} $
, the balance of mechanical energy reads
The granular temperature, T, is defined as one-third of the mean square of the particle velocity fluctuations and thus relates to R K as (3/2)T ≡ R K . Let q α be the components of the flux of fluctuation energy, and Γ the rate of collisional dissipation per unit volume. R K then has to obey the following advection–diffusion–dissipation equation:
Next, we average over z between the bed at z = 0 and the surface at z = h(
x
, t). We use the notation
u
≡ (u, v)T, u
α
≡ (u, w)T, ∂
α
≡ (∇, ∂
z
)T. The 3-D stress tensor decomposes into the 2-D tensor σ
ab
≡
σ
, the 2-D vector σ
az
= σ
za
≡
S
, and the 2-D scalar σ
zz
, with a, b∈{x, y}.
S
b is the bed shear stress. For any field ψ(
x
, z, t), the depth average can be written as
![]() $h \bar {\psi }({\bi x},\,t) \equiv \int _0^{h({\bi x},\,t)} \psi ({\bi x},\,z,\,t) {\rm d} z$
. Leibniz's rule, e.g.,
$h \bar {\psi }({\bi x},\,t) \equiv \int _0^{h({\bi x},\,t)} \psi ({\bi x},\,z,\,t) {\rm d} z$
. Leibniz's rule, e.g.,
![]() $\partial _t \int _0^h \psi ({\bi x},\,z,\,t) {\rm d} z = \int _0^h \partial _t \psi ({\bi x},\,z,\,t) {\rm d} z + \psi ({\bi x},\,h,\,t) \partial _t h({\bi x},\,t)$
, and the kinematic boundary condition,
$\partial _t \int _0^h \psi ({\bi x},\,z,\,t) {\rm d} z = \int _0^h \partial _t \psi ({\bi x},\,z,\,t) {\rm d} z + \psi ({\bi x},\,h,\,t) \partial _t h({\bi x},\,t)$
, and the kinematic boundary condition,
are repeatedly used together with the boundary conditions w(
x
, 0, t) = 0 and σ
αβ
(
x
, h, t) = 0. For simplicity, we assume the bed to be non-erodible and the density to be constant with depth. In this case, the height h is a useful variable. When the density varies strongly and the upper edge may not be well defined, it is better to work with mass hold-up
![]() $m = h\bar {\rho }$
and the centre-of-mass,
$m = h\bar {\rho }$
and the centre-of-mass,
![]() $Z = \overline {z\rho }/\overline {\rho }$
. We can rewrite the kinematic boundary condition as a volume-balance equation. Thus, the system is governed by five balance equations for, respectively, the volume, the mass, the linear momenta in the flow plane and normal to the bed, and the fluctuation energy:
$Z = \overline {z\rho }/\overline {\rho }$
. We can rewrite the kinematic boundary condition as a volume-balance equation. Thus, the system is governed by five balance equations for, respectively, the volume, the mass, the linear momenta in the flow plane and normal to the bed, and the fluctuation energy:
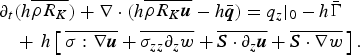 $$\eqalign{&\matrix{\partial_t (h\overline{\rho R_K}) + {\bf \nabla} \cdot(h \overline{\rho R_K {\bi u}} - h {\bar {\bi q}}) = q_z \vert_0 - h {\bar {\it \Gamma}} } \cr &\quad +\, h \left[\, \overline{{\bi \sigma}: {\bf \nabla}{\bi u}} + \overline{\sigma_{zz} \partial_z w} + \overline{{\bi S} \cdot \partial_z {\bi u}} + \overline{{\bi S} \cdot {\bf \nabla} w} \,\right ].}$$
$$\eqalign{&\matrix{\partial_t (h\overline{\rho R_K}) + {\bf \nabla} \cdot(h \overline{\rho R_K {\bi u}} - h {\bar {\bi q}}) = q_z \vert_0 - h {\bar {\it \Gamma}} } \cr &\quad +\, h \left[\, \overline{{\bi \sigma}: {\bf \nabla}{\bi u}} + \overline{\sigma_{zz} \partial_z w} + \overline{{\bi S} \cdot \partial_z {\bi u}} + \overline{{\bi S} \cdot {\bf \nabla} w} \,\right ].}$$
In addition, one must specify expressions relating the average of products of fields to the product of averages, constitutive equations relating the stresses
![]() ${\bar {\bi \sigma }}$
,
S
, σ
zz
to the fields h,
${\bar {\bi \sigma }}$
,
S
, σ
zz
to the fields h,
![]() $\bar {\rho }$
,
$\bar {\rho }$
,
![]() $\hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}$
,
$\hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}$
,
![]() $\bar {w}$
and
$\bar {w}$
and
![]() $\hskip 0.9pt\bar {\hskip -0.9ptR}_K$
, and boundary conditions for the fields and stresses. Within the stated framework, these equations are general. Note that the height equation (B8), mass balance (B9) and the z-momentum balance (B11) need to be used jointly to determine the flow depth and the density. Simplifying assumptions are needed to close the equations and to make them tractable. However, any approximations have to be compatible with the general structure of Eqns (B8)–(B12). Equation (B8) can be thought of in at least three different ways: Firstly, as we have written it here, as a volume-balance equation; secondly as a kinematic equation
$\hskip 0.9pt\bar {\hskip -0.9ptR}_K$
, and boundary conditions for the fields and stresses. Within the stated framework, these equations are general. Note that the height equation (B8), mass balance (B9) and the z-momentum balance (B11) need to be used jointly to determine the flow depth and the density. Simplifying assumptions are needed to close the equations and to make them tractable. However, any approximations have to be compatible with the general structure of Eqns (B8)–(B12). Equation (B8) can be thought of in at least three different ways: Firstly, as we have written it here, as a volume-balance equation; secondly as a kinematic equation
![]() $\partial _t h + \overline {{\bi u}}\,\cdot \,{\bf \nabla} h = w_h$
; and thirdly as an equation for the centre-of-mass h/2. This last interpretation is the most general and most useful since it corresponds to the gravitational potential energy and is well defined for any density distribution including when there is no well-defined upper surface.
$\partial _t h + \overline {{\bi u}}\,\cdot \,{\bf \nabla} h = w_h$
; and thirdly as an equation for the centre-of-mass h/2. This last interpretation is the most general and most useful since it corresponds to the gravitational potential energy and is well defined for any density distribution including when there is no well-defined upper surface.
Now we may compare these equations with the extended RKE model of [V] and [VI]. The indices Φ and Σ refer to the dense flow and the snow cover, respectively. One readily identifies M with
![]() $h\bar {\rho }$
. First, we focus on the equations for M
Φ, M
Φ
u
Φ, M
Φ
v
Φ and Rh
Φ; we will discuss the equations for h
Φ, M
Φ
w
Φ and N
K
afterwards. The left-hand sides of Eqns (B8)–(B12) agree with Eqns (VI.30) and (VI.37)–(VI.39) if one approximates the depth-averages of products of fields by the products of the depth-averaged fields, assuming uniform profiles. The source terms proposed in [VI] are summarised by the first four rows of Eqn (VI.39):
$h\bar {\rho }$
. First, we focus on the equations for M
Φ, M
Φ
u
Φ, M
Φ
v
Φ and Rh
Φ; we will discuss the equations for h
Φ, M
Φ
w
Φ and N
K
afterwards. The left-hand sides of Eqns (B8)–(B12) agree with Eqns (VI.30) and (VI.37)–(VI.39) if one approximates the depth-averages of products of fields by the products of the depth-averaged fields, assuming uniform profiles. The source terms proposed in [VI] are summarised by the first four rows of Eqn (VI.39):
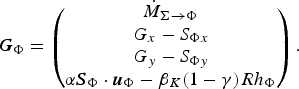 $$\eqalign{ {\bi G}_\Phi = \left(\!\matrix{ {\dot M}_{\Sigma\rightarrow\Phi} \cr G_x - S_{\Phi x} \cr G_y - S_{\Phi y} \cr \alpha {\bi S}_\Phi \cdot {\bi u}_\Phi - \beta_K \lpar 1-\gamma\rpar R h_\Phi }\!\right).}$$
$$\eqalign{ {\bi G}_\Phi = \left(\!\matrix{ {\dot M}_{\Sigma\rightarrow\Phi} \cr G_x - S_{\Phi x} \cr G_y - S_{\Phi y} \cr \alpha {\bi S}_\Phi \cdot {\bi u}_\Phi - \beta_K \lpar 1-\gamma\rpar R h_\Phi }\!\right).}$$
With the erosion rate set to 0, this becomes in our notation
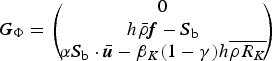 $$ {\bi G}_\Phi = \left(\!\!\matrix{ 0 \cr h{\bar \rho}{\bi f} - {\bi S}_{{\rm b}} \cr \alpha {\bi S}_{{\rm b}} \cdot\hskip 0.9pt{\bar {\hskip -0.9pt{\bi u}}} - \beta_K \lpar 1-\gamma\rpar h\overline{\rho R_K} }\!\! \right)$$
$$ {\bi G}_\Phi = \left(\!\!\matrix{ 0 \cr h{\bar \rho}{\bi f} - {\bi S}_{{\rm b}} \cr \alpha {\bi S}_{{\rm b}} \cdot\hskip 0.9pt{\bar {\hskip -0.9pt{\bi u}}} - \beta_K \lpar 1-\gamma\rpar h\overline{\rho R_K} }\!\! \right)$$
[V] and [VI] model the term
![]() ${\bf \nabla}\,\cdot \,(h\bar {{\bi \sigma }})$
on the left-hand side of (B8) as
${\bf \nabla}\,\cdot \,(h\bar {{\bi \sigma }})$
on the left-hand side of (B8) as
![]() $(1/2){\bf \nabla}(\bar {\rho } h^2 g_z)$
and neglect shear stresses in vertical planes (as virtually all quasi-3-D avalanche models do). The RKE-modified Voellmy friction law is used to model the bed shear stress
S
b – however, now with R
V
instead of R
K
determining the decrease of the friction parameters (cf. Eqns (VI.35) and (VI.36)). The slope-parallel diffusive flux of RKE is neglected (
q
≈ 0), as mentioned earlier. In (B11), the dissipation Γ is assumed proportional to R
K
+ R
V
= R
K
− M(k − k
0)g
z
rather than to R
K
3/2 as suggested by kinetic theory. Neither the different exponent nor the appearance of R
V
in Γ is incompatible with the general framework because the latter does not specify the form of Γ, but it is a clear departure from kinetic theory.
$(1/2){\bf \nabla}(\bar {\rho } h^2 g_z)$
and neglect shear stresses in vertical planes (as virtually all quasi-3-D avalanche models do). The RKE-modified Voellmy friction law is used to model the bed shear stress
S
b – however, now with R
V
instead of R
K
determining the decrease of the friction parameters (cf. Eqns (VI.35) and (VI.36)). The slope-parallel diffusive flux of RKE is neglected (
q
≈ 0), as mentioned earlier. In (B11), the dissipation Γ is assumed proportional to R
K
+ R
V
= R
K
− M(k − k
0)g
z
rather than to R
K
3/2 as suggested by kinetic theory. Neither the different exponent nor the appearance of R
V
in Γ is incompatible with the general framework because the latter does not specify the form of Γ, but it is a clear departure from kinetic theory.
To the extent that Bartelt and co-workers assume the shear layer to be infinitesimally thin, the supply of RKE could be described by setting the boundary flux term
![]() $q_z \vert_0 = \alpha {\bi S}_{{\rm b}} \cdot \hskip 0.9pt \bar {{\hskip -0.9pt{\bi u}}}$
. But it appears more natural to regard α
S
b ·
u
|0 as the limit of
$q_z \vert_0 = \alpha {\bi S}_{{\rm b}} \cdot \hskip 0.9pt \bar {{\hskip -0.9pt{\bi u}}}$
. But it appears more natural to regard α
S
b ·
u
|0 as the limit of
![]() $h {\overline {\bi S}\,\cdot \,\partial _z {\bi u}}$
when the thickness of the shear layer, δ
s, tends to zero: in the shear layer, the shear stress is approximately equal to
S
b, and the shear rate is
$h {\overline {\bi S}\,\cdot \,\partial _z {\bi u}}$
when the thickness of the shear layer, δ
s, tends to zero: in the shear layer, the shear stress is approximately equal to
S
b, and the shear rate is
![]() $\partial _z {\bi u} \,\approx \hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}/\delta _s$
. Integration over z from 0 to h then gives
$\partial _z {\bi u} \,\approx \hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}/\delta _s$
. Integration over z from 0 to h then gives
![]() ${\bi S}_b \cdot \, (\bar {{\hskip -0.9pt{\bi u}}}/\delta _s) \delta _s = {\bi S}_b \,\cdot \hskip 0.9pt \bar {{\hskip -0.9pt{\bi u}}}$
. This would, however, impose α = 1.
${\bi S}_b \cdot \, (\bar {{\hskip -0.9pt{\bi u}}}/\delta _s) \delta _s = {\bi S}_b \,\cdot \hskip 0.9pt \bar {{\hskip -0.9pt{\bi u}}}$
. This would, however, impose α = 1.
The extended RKE model of [V] and [VI] thus neglects all terms on the second line of Eqn (B12) except the third. The first and fourth terms describe RKE generation due to shear along the vertical planes. According to the standard scaling arguments for shallow flows based on the aspect ratio ε ≪ 1,
![]() $\hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}$
and ∂
z
are O(1) while h, w and ∇ are O(ε). Thus, only the third term,
$\hskip 0.9pt\bar {{\hskip -0.9pt{\bi u}}}$
and ∂
z
are O(1) while h, w and ∇ are O(ε). Thus, only the third term,
![]() $h \overline {{\bi S}\,\cdot \,\partial _z {{\bi u}}}$
, is O(ε) while the others are O(ε
2) or O(ε
3) and would be negligible. However, the second term,
$h \overline {{\bi S}\,\cdot \,\partial _z {{\bi u}}}$
, is O(ε) while the others are O(ε
2) or O(ε
3) and would be negligible. However, the second term,
![]() $h\overline {\sigma _{zz}\partial _z w}$
, is special in that it is present even if the flow does not deform in the tangential directions of the incline, but changes density. Moreover, it describes how RKE is transformed into potential (i.e., non-random) kinetic energy as the flow expands in the bed-normal direction. This term thus implements the feed-back mechanism governing density changes and must not be discarded. A more detailed scale analysis of Eqn (B11) would need to introduce different timescales and is beyond the scope of this paper, but will be invaluable in the construction of an improved, consistent model.
$h\overline {\sigma _{zz}\partial _z w}$
, is special in that it is present even if the flow does not deform in the tangential directions of the incline, but changes density. Moreover, it describes how RKE is transformed into potential (i.e., non-random) kinetic energy as the flow expands in the bed-normal direction. This term thus implements the feed-back mechanism governing density changes and must not be discarded. A more detailed scale analysis of Eqn (B11) would need to introduce different timescales and is beyond the scope of this paper, but will be invaluable in the construction of an improved, consistent model.
Finally, comparing the last three equations in the system (VI.30), (VI.37)–(VI.39),
with Eqn (B11) is not straightforward because the extended RKE model here departs from the canonical approach based on the fundamental balance equations. We first note that, if one assumes uniform density and velocity profiles, one may insert Eqn (B9) into Eqn (B11) to obtain
Using the equation for M
Φ with
![]() $\dot {M}_{\Sigma \rightarrow \Phi }$
, which is identical to Eqn (B9), the same procedure can be applied to Eqn (B15) and yields (in our notation)
$\dot {M}_{\Sigma \rightarrow \Phi }$
, which is identical to Eqn (B9), the same procedure can be applied to Eqn (B15) and yields (in our notation)
The neglected term is O(ε), thus smaller than each of the other two terms on the right-hand side of Eqn (B17), but of the same order as D t w and the sum of the O(1) terms. Equation (B14) appears to contain a misprint – w Φ is the centre-of-mass velocity, thus there should be a factor 2 on the right-hand side. Even so, this equation is in conflict with the kinematic boundary condition (B7) because ∇ · u Φ ≢ 0. In fact, tracing its derivation in [VI], one sees that it should be the kinematic boundary condition rather than a dynamical equation. We have discussed the reasons why Eqn (B16) is not valid in Section 3; comparing it with Eqn (B11), it is apparent that it needs to be replaced by a proper constitutive law for σ zz or, equivalently, the pressure.




