Cyclic strengthening of lake ice

Abstract

Further to systematic experiments on the flexural strength of laboratory-grown, fresh water ice loaded cyclically, this paper describes results from new experiments of the same kind on lake ice harvested in Svalbard. The experiments were conducted at −12 °C, 0.1 Hz frequency and outer-fiber stress in the range from ~ 0.1 to ~ 0.7 MPa. The results suggest that the flexural strength increases linearly with stress amplitude, similar to the behavior of laboratory-grown ice.

Introduction

The propagation of ocean swells into a floating ice cover has led, in at least a few recorded instances, to the sudden break-up of the ice cover into smaller ice floes (Asplin and others, 2012; Collins and others, 2015; Kohout and others, 2016). In these works, the sudden break-up of first-year and multi-year ice was observed due to wave action which is discussed in Ardhuin and others (2020). These observations raise a question about the effect of cyclic loading on the mechanical behavior of ice. From a practical perspective, this question is relevant not only to floating ice covers that form on cold lakes and oceans and these were investigated previously in the laboratory and in situ in the field (Mellor and Cole, 1981; Nixon and Smith, 1987; Cole, 1990, 1998; Haynes and others, 1993; Cole and Durell, 1995; Haskell and others, 1996; Langhorne and Haskell, 1996; Bond and Langhorne, 1997; Weber and Nixon, 1997; Cole and others, 1998; Gupta and others, 1998; Langhorne and others, 1998, 1999, 2001; Iliescu and Schulson, 2002; Cole and Dempsey, 2004), but also to the stability of floating ice shelves (Holdsworth, 1969; Vinogradov and Holdsworth, 1985; Sergienko, 2010), accretion of atmospheric ice on power transmission lines (Kermani and Farzaneh, 2009) and, under tidal forcing of an extraterrestrial origin, the strength of the icy crust of Jupiter's Europa and of Saturn's Enceladus (Burns and Matthews, 1986; Hammond and others, 2018). With that in mind, we recently performed systematic experiments (at −25 to −3^o C at 0.03–2 Hz) on the behavior under 4-point cyclic loading of columnar-grained S2 fresh water ice produced in the laboratory and loaded across the long axis of the columns (Iliescu and others, 2017; Murdza and others, 2018, 2019, 2020). We found that the flexural strength increased upon cycling, scaling linearly with the amplitude of the outer-fiber stress (0.1–2.6 MPa) and reaching a factor of two or more greater than the noncycled strength. Is this behavior, we wondered, a characteristic also of ice produced under natural conditions? To explore this point, we performed similar experiments on lake ice. This paper describes our results.

Procedure

We harvested the ice from the ~50 cm thick cover on a lake in the Arctic, located near Mine 7 in Longyearbyen, Svalbard. The ice was characterized by columnar-shaped grains of 17 ± 3 mm diameter, Figure 1, an S2 growth texture (c-axis was randomly oriented within the horizontal plane of the parent ice cover and confined within ~15° to that plane), and a density of 915 kg m⁻³. From large (~120 cm  × 70 cm  × 50 cm) blocks cut from the cover and then transported to and stored at UNIS, we fabricated plate-shaped specimens of dimensions h ~ 45 mm in thickness (parallel to the long axis of the grains), b ~ 100 mm in width and l ~ 600 mm in length. The specimens were equilibrated at −12 °C and then nonreversely loaded across the columns at 0.1 Hz at an outer-fiber stress in the range from ~ 0.1 to ~ 0.7 MPa, using a custom-built 3-point bending rig, Figure 2, attached to a uniaxial loading system termed ‘Knekkis’ (for details on Knekkis see Nanetti and others (2008); Sukhorukov and Marchenko (2014)). The specimens were free from cracks, at least of a size detectable by the unaided eye, but contained a few narrow (< 1 mm dia.) air channels oriented parallel to the long axis of the grain columns.

Fig. 1. Photographs showing the microstructure of lake ice: horizontal (a) and vertical (b) thin sections.

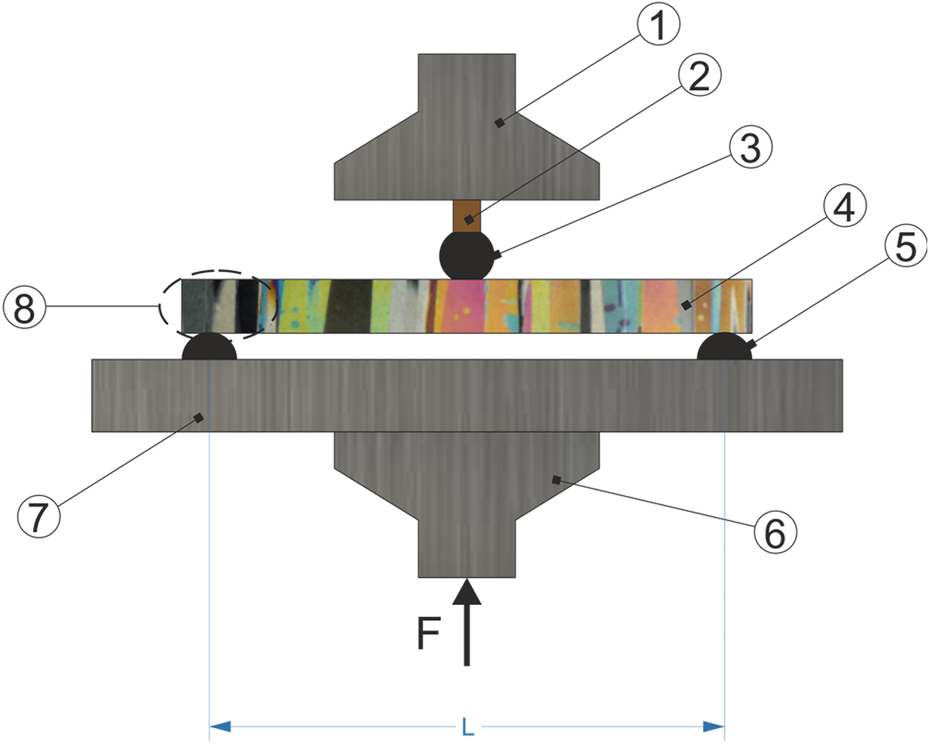
Fig. 2. Sketch of the three-point bending apparatus connected to a ‘Knekkis’ mechanical testing system: 1 – immobile steel plate; 2 – HBM load cell; 3 – mid-loading span; 4 – ice specimen; 5 – outer loading span; 6 – loading press; 7 – steel plate; 8 – schematics of columns within the ice specimen. The upper immobile part 1 is attached to the frame of the machine while the mobile lower part 6 is attached through a fatigue-rated load cell to the piston.

To load and then unload the specimen, the mechanical actuator of ‘Knekkis’ was driven up and down under displacement control with the displacement limited in both directions. In addition to a built-in load cell, an external more accurately calibrated HBM load cell was placed between the middle loading span and the press. The results showed there was no significant difference in measurements made using the two load cells. The displacement of the top surface of the ice plate was measured using three calibrated HBM LVDT gauges and the outer-fiber stress σ _f was calculated from the relationship:

(1)$$\sigma _f = \displaystyle{{3PL} \over {2bh^2}}\;\;\comma \;$$

where P denotes the applied load, L is the load span (460 mm) and b and h the dimensions noted above.

Results and observations

Firstly, we conducted three tests where the flexural strength of noncycled ice was measured. Table 1 lists the results. The average and Std dev. of the measured flexural strength are 1.52 ± 0.04 MPa which indicates good reproducibility. These values compare favorably with the values of 1.73 ± 0.25 MPa reported by Timco and O'Brien (1994) for S2 fresh water ice at temperatures below −4.5 °C and with the values of 1.67 ± 0.22 MPa reported by Murdza and others (2020) for S2 fresh water ice at −10 °C.

Table 1. Flexural strength of both noncycled and cycled lake ice samples

Subsequently, we cycled four specimens in a nonreversed manner for a certain number of cycles (up to 12 000) and then brought the ice to a forced monotonic failure by bending in the same sense as cycled. Table 1 lists the stress amplitude during cycling, the number of cycles imposed and the flexural strength after cycling. Figure 3 plots the flexural strength versus amplitude of outer-fiber stress and compares the present results with those obtained earlier (Murdza and others, 2020) from laboratory-grown ice. Despite somewhat different loading conditions and a different origin of ice, specified in Table 2, the lake ice appears to behave similarly to the laboratory-grown ice under cycling: its flexural strength increases in an apparent linear manner as stress amplitude (and outer-fiber stress) increases.

Table 2. Comparison of the test setup and ice parameters between laboratory-grown ice (Murdza and others, 2020) and present lake ice

^a Density of ice grown in the same manner is taken from Golding and others (2010).

^b In the nonreversed experiments, frequency is lower by a factor of two than in the reversed experiments at the same conditions.

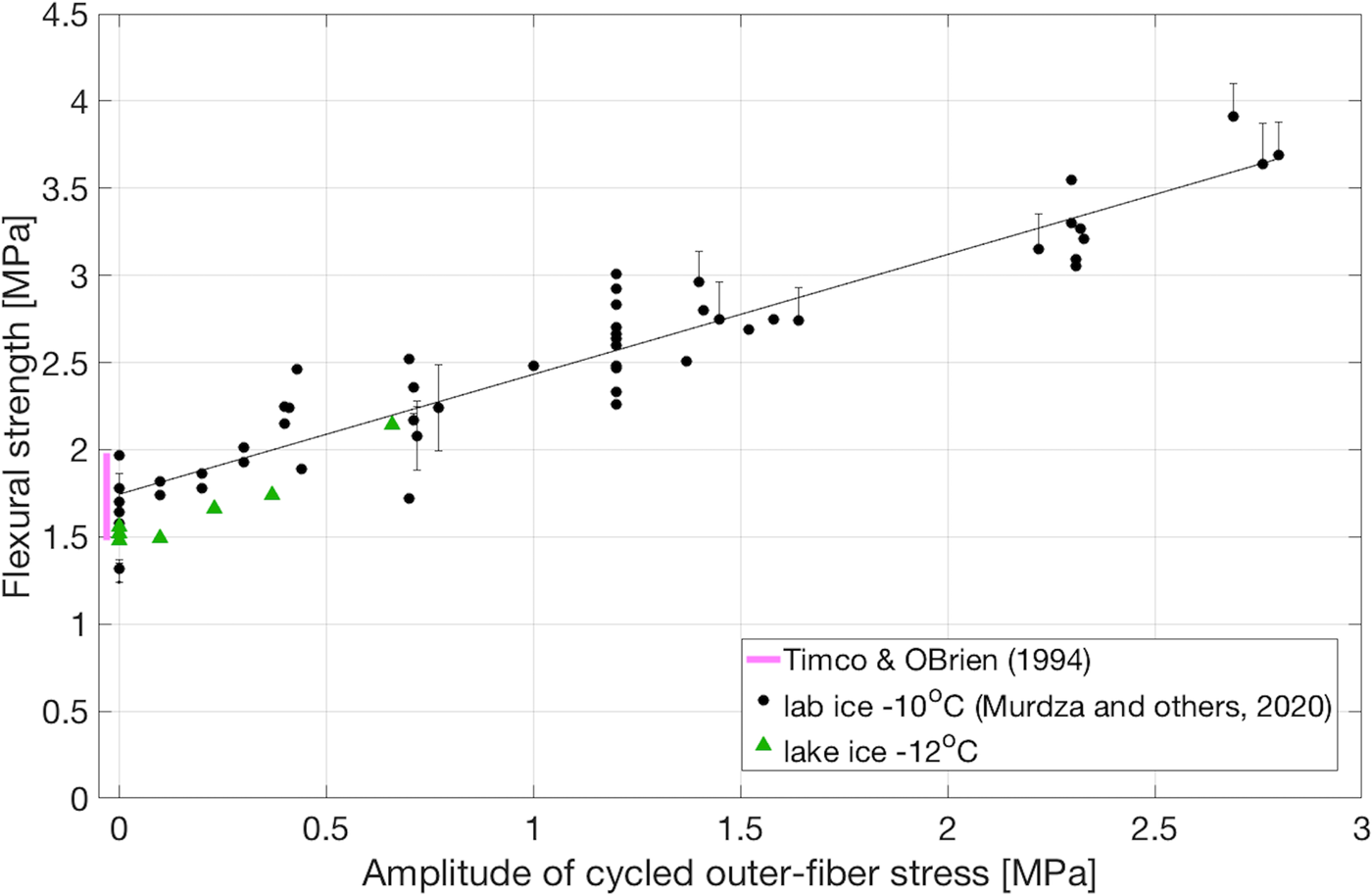
Fig. 3. Flexural strength of fresh water ice as a function of stress amplitude/average amplitude of outer-fiber stress during cycling. The solid pink line indicates the average flexural strength of noncycled fresh water ice plus and minus one standard deviation, i.e. 1.73 ± 0.25 MPa (Timco and O'Brien, 1994). Black points represent laboratory tests presented in Murdza and others (2020) which were conducted on laboratory-grown fresh water ice at −10 °C and 0.1 mm s⁻¹ outer-fiber center-point displacement rate in a reversed manner. Green points represent new tests on the lake ice. During all depicted tests the ice did not fail during cycling but was broken by applying one unidirectional displacement until failure occurred.

In all tests, failure occurred in the midpoint of the sample, i.e. beneath the mid-loading span. Interestingly, that this place is the most ‘strained’ zone within the sample given that the degree of strengthening depends on the outer-fiber stress amplitude and that the outer-fiber stress reaches its maximum in the midpoint of a specimen in 3-point bending test. Therefore, the location of ice failure is an important characteristic of an experiment as it may indicate the dependence of flexural strength on the stress amplitude. This is different from the 4-point bending test where the peak outer-fiber stress is produced along an extended region between inner loading spans and, therefore, failure occurs randomly within the middle section.

In contrast to experiments reported by Iliescu and others (2017) and Murdza and others (2020), where samples were cycled between two specified load limits, in the present experiments specimens were cycled between two specified displacement limits. We observed inelastic deformation during cycling and, as a result, both mean load and maximum load per cycle gradually decreased during cycling. Therefore, stresses in Figure 3 and Table 1 are the average amplitudes of outer-fiber stresses.

It is worth noting that, similarly to the earlier experiments on laboratory-grown ice (Murdza and others, 2020), acoustic emissions were essentially not detected above minimum AE amplitude detection of 45 dB (unlike Langhorne and Haskell, 1996; Cole and Dempsey, (2004, 2006); Lishman and others, 2020) until the ice broke into two pieces and that the remnant pieces contained no cracks large enough to be detected by eye. This means that the flexural strength of both the lake ice and the lab ice was governed by the tensile stress to nucleate the first crack.

Not detected by the unaided eye in the present experiments were grain boundary decohesions (Ignat and Frost, 1987; b; Nickolayev and Schulson, 1995, Picu and Gupta, 1995a; Gupta and others, 1997; Weiss and Schulson, 2000; Frost, 2001). Features of that kind were quite prominent in earlier tests (Iliescu and others, 2017; Murdza and others, 2020) and were taken to be evidence of grain boundary sliding. That we did not observe them here does not necessarily mean that grain boundary sliding did not occur. Fewer grains boundaries appropriately oriented for sliding were located within the narrow region of highest tensile stress in 3-point bending (present case) and so this could account for the apparent absence of decohesions.

Discussion

Although the physical process underlying cyclic strengthening is not the focus of this letter, our sense is that the process is probably similar to the one discussed in Murdza and others (2020) for laboratory-grown ice; namely the development of an internal back-stress that opposes the applied stress in nucleating cracks. It may be significant that of the two possible mechanisms proposed earlier (Murdza and others, 2020) for generating back-stress, namely dislocation pileups and grain boundary sliding, the latter may be the less likely, given that the strengthening measured in the present experiments is very close to that measured earlier, yet decohesions were not detected. However, given that under a 3-point bending much smaller volume of ice is subjected to the critical stress compared with a 4-point bending, there could be no grain boundaries that are favorably oriented for grain boundary sliding. Indeed, Figure 10 in Murdza and others (2020) shows that not all the boundaries are favorably oriented for decohesion development. Therefore, further work is required to elucidate the underlying physics.

Lastly, we would like to caution the reader to not necessarily expect the strengthening of every lake ice upon cycling; for example, in the case of lake ice with c-axis oriented vertically, no shear stress acts on basal planes when the ice cover is flexed and so the results can be different.

Conclusions

New results, although few in number, indicate that ice produced under natural conditions on an Arctic lake when flexed in the laboratory in a nonreversed manner under 3-point loading at −12 °C and 0.1 Hz, is strengthened upon cycling. In other words, cyclic strengthening appears to be a characteristic of ice per se and not of its origin nor of the exact method of cycling.