Densification of layered firn of the ice sheet at NEEM, Greenland

Abstract

Densification of firn at the North Greenland Eemian Ice Drilling (NEEM) camp is investigated using density surrogates: dielectric permittivities ∊v and ∊h at microwave frequencies with electrical fields in the vertical and horizontal planes, respectively. Dielectric anisotropy Δ_∊ (= ∊_v − ∊_h) is then examined as a surrogate for the anisotropic geometry of firn. Its size, fluctuations and mutual correlations are investigated in samples taken at depths from the surface to ~90 m. The initial Δ∊ of ~0.06 appears within the uppermost 0.2 m. After that, Δ_∊ decreases rapidly until 21–26 m depth. Below this, Δ_ɛ decreases slowly. Layers with more ions of fluorine, chlorine and some cations deposited between the autumn and the subsequent summer deform preferentially during all these stages. This layered deformation is explained partly by the textural effects initially formed by the seasonal variation of metamorphism, and partly by ions such as fluorine, chlorine and ammonium, which are known to modulate dislocation movement in the ice crystal lattice. Insolation-sensitive microstructure appears to be preserved all the way to the pore close-off, within layers of the summer-to-autumn metamorphism. Like previous authors, we hypothesize that calcium is not the active agent in the reported deformation– calcium correlations.

1. Introduction

Knowledge of the densification of snow into ice is an important basis for better understanding the various physical processes occurring within polar ice sheets. Once deposited, snow undergoes initial metamorphism processes depending on temperature, temperature gradient, accumulation rate, wind and other surface conditions (e.g. Colbeck, 1989; Cuffey and Paterson, 2010). It subsequently undergoes densification associated with mechanisms such as structural rearrangement of grains, pressure sintering, plastic deformation, recrystallization and fractures (e.g. Bader, 1939; Benson, 1962; Anderson and Benson, 1963; Gow, 1968, 1975; Maeno and Ebinuma, 1983; Alley, 1988; Hondoh, 2000; Fujita and others, 2009; Kipfstuhl and others, 2009; Cuffey and Paterson, 2010; Hörhold and others, 2011, 2012; Lomonaco and others, 2011). Along with the results of this study, Figure 1 shows the three classic stages of firn densification as outlined in the early studies of firn processes cited above.

Fig. 1. Schematic of the evolution of layered densification at NEEM. The general main stages of firn densification (I–III) are given at the bottom. Depth-dependent layered densification is expressed as dielectric permittivity (right axis) and density (left axis) with increasing depth (bottom axis). Based on data of the present study, the upper and lower limits and the mean values of_h are shown. Both the upper and lower limits deviate from the mean by 2σ.

Bender (2002) discovered that the orbital tuning chronology for the Vostok (East Antarctica) deep ice core was supported by the trapped gas composition. This discovery has stimulated recent firn studies. Various factors have been found to influence the physical processes of firn. Some studies highlighted the possible significance of an insolation imprint on the physical properties of firn (e.g. Bender, 2002; Kawamura and others, 2007; Fujita and others, 2009; Hutterli and others, 2009). A correlation between deformation and impurities such as calcium (Hörhold and others, 2012; Freitag and others, 2013) was empirically found. Several studies also suggested ‘density crossover’ in firn (Gerland and others, 1999; Freitag and others, 2004; Fujita and others, 2009; Hörhold and others, 2011). This phenomenon is the local convergence of density fluctuations at a density of ~600 kg m⁻³, commonly found in polar firn. Ice-core researchers also recognized that in the air trapped in ice cores, gas fractionations such as O₂/N₂ ratio and total air content (TAC) are strongly associated with firn densification processes (Bender, 2002; Kawamura and others, 2004, 2007; Raynaud and others, 2007; Suwa and Bender, 2008; Fujita and others, 2009; Hutterli and others, 2009; Lipenkov and others, 2011; Landais and others, 2012).

Despite these recent advances, many important questions remain unanswered. For example, local insolation imprint effects including ice-core gas results (O₂/N₂ ratio and TAC) have been discussed mostly for East Antarctic plateau sites. Fujita and others (2009) proposed that metamorphism of the layered firn at Dome Fuji (Dome F) is a major mechanism for local insolation modulation of gas transport conditions during pore close-off. That is, seasonal variations of meta-morphism modulate the mechanical strength of layered firn due to textural effects such as ice–ice bonding, cluster strength of the c –axis around the vertical axis and anisotropic geometry of ice and pore spaces. Hereinafter, we refer to the mechanical effects from these as ‘textural effects’. However, no studies for dome plateau sites in East Antarctica have examined the possible impurity-softening effect proposed by Freitag and others (2004) and Hörhold and others (2012). As for Greenland ice cores, Suwa and Bender (2008) reported that the O₂/N₂ ratio at the Greenland Ice Sheet Project 2 (GISP2) site is correlated with local summer insolation. However, in terms of firn densification processes, the only possible correlations of densification with impurities such as calcium were noted for sites in Greenland and some East Antarctic coastal sites with relatively low elevation (<~3000 m) (Hörhold and others, 2012; Freitag and others, 2013). In terms of impurities, the correlations between local summer insolation, O₂/N₂ ratio and TAC were not explained (Hörhold and others, 2012). In addition, these papers did not examine possible textural effects. Therefore, the possible roles of summer insolation and various ions must be examined more closely in both Greenland and Antarctica at various elevations. The possible roles of impurity-based softening must also be explored at major deep ice-coring sites in the East Antarctic plateau (e.g. Dome F, Vostok and Dome C).

Here we investigate firn densification at the North Greenland Eemian Ice Drilling (NEEM) camp, northwest Greenland (77.45° N, 51.06° W; surface elevation 2450 m; mean annual temperature –29°C; accumulation 0.22 m ice equivalent a⁻¹) (NEEM Community Members, 2013). A 2540 m long ice core was drilled through the ice during the years 2008–12. We used ‘2010-S3’, which was one of the firn cores drilled down to 88.55 m depth in 2010 in the vicinity of the deep coring site. We also used firn samples dug from a 2 m pit in the 2012 field season. We measured the dielectric permittivity tensor at ~34 GHz, as surrogates for both density and geometrical anisotropy, as explained below. The dielectric permittivity of ice, firn and snow at high frequencies such as short radiowave (MHz) and microwave (GHz) ranges under the temperature range of the cryosphere is primarily dependent on density (Cumming, 1952; Tiuri and others, 1984; Hallikainen and others, 1986; Denoth, 1989; Kovacs and others, 1995; Mätzler, 1996; Fujita and others, 2000). It also depends on temperature (Gough and Davidson, 1970; Gough, 1972; Johari and Charette, 1975; Johari and others, 1984; Mätzler and Wegmüller, 1987; Fujita and others, 1993; Matsuoka and others, 1997) and crystal orientations (Fujita and others, 1993; Matsuoka and others, 1997). Anisotropy in the geometrical structure of ice and pore in firn also causes anisotropy in the dielectric permittivity, which can reach ~0.08 (Lytle and Jezek, 1994; Fujita and others, 2009). This effect is often much larger than the dielectric anisotropy due to crystal orientation fabrics in the polar firn (<~0.01) (Fujita and others, 2009). Therefore, using the dielectric permittivity tensor of firn, we can determine the evolution of both the density and anisotropic structure of ice and pore. We also investigate major ions and the oxygen isotope ratio of the samples to explore possible links between densification, impurities and seasonal origin of the deposition. Our proposals added to classical views are schematically shown in Figure 1. In this paper, we develop data and discuss how our proposals were derived.

This paper sheds new light on the twin puzzles of how impurities accelerate densification of firn and how O₂/N₂ ratios and TAC in mature ice can seemingly record local insolation variations. In Section 2, we summarize methods of measurement and samples. In Section 3, as results of measurements, we present dielectric permittivity vs depth and density. Effects of impurities are also investigated. The discussion first, in Section 4.1, looks at the initial state of layering near the surface, in terms of density, ∊_v, ∊_h, Δ_∊, chemical ions and their seasonality. Then, in Section 4.2, we discuss the evolution of density and the anisotropic structure within firn down to the pore close-off. The three stages shown in Figure 1 are discussed in detail. In Section 4.3 we discuss correlations between deformation, impurities and seasonal effects. We try to find physical links between deformation and impurities. We then, in Section 4.4, discuss the textural effects on mechanical properties of firn caused by summer-to-autumn metamorphism. Finally, we summarize our picture of firn evolution and of the meaning of the dielectric anisotropy at NEEM. The relevance of the geometrical anisotropy to the O₂/N₂ puzzle is discussed in terms of the persistently less deformable nature of the summer-to-autumn layers.

2. Method of Measurement and Samples

2.1. Dielectric permittivity measurement

We used an open resonator method to measure the tensorial components of dielectric permittivity continuously along the depths of firn samples. The method was described by Jones (1976a,b), and applied to ice and firn studies (Matsuoka and others, 1997, 1998; Fujita and others, 2009). It is suitable for precise measurement of dielectric permittivity components and dielectric anisotropy for long slab-shaped samples. A semi-confocal-type open resonator, having a concave mirror with a 200 mm curvature radius and a 186 mm distance between two mirrors, was designed for measurements in the Ka band (26.5–40 GHz). Appropriate sets of frequency and sample thickness are important to minimize experimental errors and achieve precise measurements (Jones, 1976b; Komiyama, 1991). The slab-shaped samples were made using a microtome. A typical sample was 550 mm long, 4.8–7.0 mm thick and 60 mm wide. Sample thicknesses were set to be as thick as the average wavelength of the electromagnetic wave within the sample in the resonator. The sample width needed to be sufficiently larger than the half-power diameter, 22 mm, of the Gaussian distribution of the resonant wave. The measurement temperature was –16.0 ± 1.5°C. The measured permittivity was a volume-weighted average within this Gaussian distribution of the electromagnetic wave in the slab-shaped sample. Each sample was inserted into the center of the electrical field at increments of 5 mm. Permittivity components in both the vertical and horizontal planes of the ice sheet (denoted as_v and_h, respectively) were measured simultaneously by applying the physical principle of birefringence (Jones, 1976b). We confirmed that, by rotating the electrical field vector within the measured samples of firn,_v was always larger than_h. Three sets of resonant frequencies of TEM0,0, q (q: integer) modes (Jones, 1976b; Komiyama, 1991) between 33.6 and 35.0 GHz were chosen. The errors associated with sample thickness variations (<0.1 mm) were minimized by solving equations (Jones, 1976b; Komiyama, 1991) for multiple resonant frequencies simultaneously to find a unique solution of dielectric permittivity with a common sample thickness. Final errors in the permittivity and in the dielectric anisotropy Δ_∊ (= ∊_v − ∊_h) were ±0.005 and ±0.001, respectively. The errors in Δ_∊ were markedly smaller than the permittivity errors due to the physical principle of the measurement of the difference of the two resonant frequencies at once (Matsuoka and others, 1997).

2.2. Samples and analysis of oxygen isotope ratio, impurities and density

Samples were taken from each of 12 portions of 2.0 m long or 1.65 m long sections with depths ranging from 0 m (surface) to 89.65 m. The 12 portions are labelled a–l. Four samples were taken from portion a and three from each of the other portions b–l. The samples are listed in the Appendix, along with statistics of the measured results. More details are presented in the following.

2.2.1. Firn-core samples

To investigate the general trend of densification, 11 portions of the 1.65 m sections were selected. A length of 1.65 m means that several annual cycles can be observed within each section. An actual unit sample was a 0.55 m long piece of core. In all, we used 33 pieces of 0.55 m long samples. After drilling the 2010-S3 core in 2010 at NEEM, pieces of the samples were transported to the National Institute of Polar Research (NIPR), Tokyo. The preservation temperature was set at 223 K to prevent deterioration until measurements were performed in 2012. The core density was measured first at NEEM and then at NIPR using the bulk density method. Dielectric permittivity measurements, analyses of the oxygen isotope ratio and major ions were performed at NIPR. For measurements of the oxygen isotope ratio and major ions, the resolution of the depth measurements was 40 mm at a shallow depth to 25 mm at greater depths. Approximately ten samples could be taken from an annual layer. The instrument used to measure the oxygen isotope ratio was the Delta V mass spectrometer (Thermo Fisher Scientific). Two ion chromatographs, DX500 (Dionex), were used to measure the cations (Na⁺, K⁺, Mg²⁺, Ca²⁺ and NH₄ ⁺) and anions (Cl⁻, SO₄ ²⁻, NO₃ ⁻, F⁻ and several others).

2.2.2. Pit samples

Samples from the uppermost 2 m were block samples of a snow pit. They were collected on 2 and 3 July 2012. We used four pieces of 0.5 m long sample, and the measurements were performed at NIPR within a year. The core density was measured first at NEEM with 30 mm resolution in a pit-wall study, and then at NIPR by the gamma-ray transmission method (e.g. Gerland and others, 1999). As with the firn cores, further measurements and analyses were carried out at NIPR. For measurements of both oxygen isotope ratio and major ions, the resolution of the depth measurements was 30 mm. The Picarro L2120-i isotopic water ionizer was used to measure oxygen isotope ratio. The two ion chromatographs used were the same as for the firn-core samples. In addition, a high-precision gamma-ray density meter (Nanogray Inc. model PH-1100, http://www. nanogray.co.jp/products/) (Miyashita, 2008) was used to determine density at 3.3 mm resolution. It was calibrated using pure ice.

3. Results

3.1. Dielectric permittivity vs depth and density

Examples of the dielectric permittivities in four selected depth ranges are shown in Figure 2. The depth ranges shown are near the surface (~6 m), in the approximate depth range of firn/ice transitions (~65 m) and intermediate depth ranges (~16 and ~32 m). Permittivity components ∊_v and ∊_h increase with increasing depth (upper panels of Fig. 2a–d); dielectric anisotropy Δ_∊ decreases with increasing depth (lower panels of Fig. 2a–d). They show large fluctuations with various fluctuation amplitudes and correlations, as discussed below. Measurements of the three components ∊_v, ∊_h and Δ_∊ with increasing depth are plotted in Figure 3. The graph shows large-scale tendencies and fluctuations. Large-scale tendencies are also shown in Figure 4 for the permittivity components in relation to the average density of each 0.55 m long sample (or 0.50 m long pit sample)._v and_h increase with increasing average density, and Δ_∊ decreases with increasing average density. We note that within the shallowest 0.5 m, Δ_∊ reaches very high values from 0.04 to 0.07. As shown further below (Fig. 8), the initial Δ_∊ of ~0.06 appears within the uppermost 0.2 m. Within several meters of the surface, Δ_∊ is large. For the large-scale tendencies, the increase of permittivity as a function of depth and density is smooth, without any visible sudden change in the gradient. In contrast, Δ_∊ decreases rapidly from ~0.06 near the surface to ~0.02 in the depth range 21–26 m, where density ρ is ~580–620 kg m⁻³. In this density range and at greater depths, Δ_∊ decreases only slowly to ~0.01 at depths near 90 m, where ρ is ~870 kg m⁻³. At ρ = 820–870 kg m⁻³, the gradient of Δ_∊ is steeper (Figs 3 and 4).

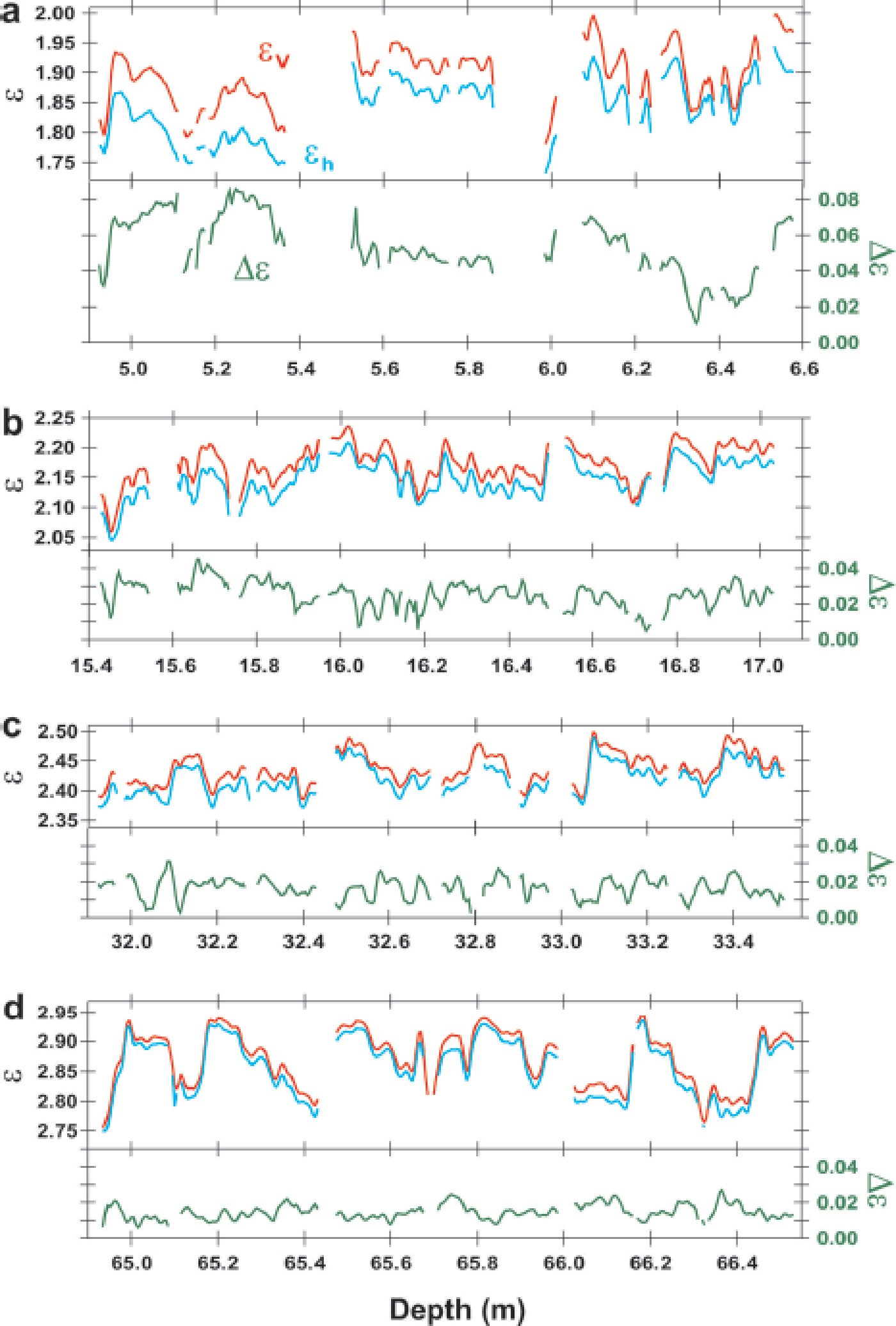
Fig. 2. Examples of dielectric permittivities along depths for four depth ranges of the 1.65 m span. The bottom axis indicates the depth of the ice sheet from the surface. The left and right axes indicate permittivities and Δ_∊ (=∊_v − ∊_h), respectively. The red lines represent ∊_v, the blue lines ∊_h and the green lines Δ_∊. We observe that ∊_v is always larger than ∊_h. These four depth ranges are denoted in later figures as depth ranges b, c, e and i from all 12 depth ranges a–l.

Fig. 3. Evolution of the three components ∊_v, ∊_h and Δ_∊ with increasing depth. The bottom axis indicates the depth of the ice sheet from the surface. The left and right axes indicate permittivities ∊ and Δ_∊, respectively, where ∊_v (red dots), ∊_h (blue dots) and Δ_∊ (green dots) are the raw data from measurements. Data from 12 depth ranges are shown. The top 2 m (a) is from a pit study. The other 11 depth ranges (b–l) are selected depth ranges of the 1.65 m span. The solid lines are fits of polynomial functions for ∊_v, ∊_h and Δ. With increasing depth, ∊_v and ∊_h increase, and the difference between them decreases. Δ_∊ has large values near the surface (Fig. 4), decreases rapidly until ~20 m depth, then has a slower decrease. For depths more than ~70 m, the gradient of Δ_∊ is again steeper.

Fig. 4. Evolution of the three components ∊_v (red), ∊_h (blue) and Δ_∊ (green) as functions of the average density of each 0.55 m long sample. The left and right axes are permittivities and Δ, respectively. The symbols and error bars are averages and standard deviations, respectively, over each 0.55 m long core segment. For the 2 m deep pit, a 0.50 m span is used instead of 0.55 m. The profiles are fitted curves for the polynomial functions. With increasing density, ∊_v and ∊_h increase, and the difference between them decreases. Δ_∊ has large values near the surface, decreases rapidly until the density range ~580–620 kg m⁻³, then decreases more slowly. For densities more than ~820 kg m⁻³, the gradient of Δ_∊ is again steeper.

Fluctuations of ∊_v and ∊_h are large in the shallowest samples (Fig. 2a), smaller in samples from intermediate depths (Fig. 2b and c) but larger again at ~65 m depth (Fig. 2d). This depth-dependent size of the fluctuations is also apparent in Figures 3 and 4. In Figure 5, the standard deviations of_v and_h within each 0.55 and 0.50 m long sample are plotted as a function of depth (Fig. 5a) and density (Fig. 5b). The standard deviations (hereinafter, σ _v and σ _h) have local minima in the depth range ~21–26 m and density range ~580–620 kg m⁻³. Using an arbitrary threshold of 0.04, σ _v and σ _h have broad maxima over the depth range 45– 72 m and density range 730–830 kg m⁻³. In contrast, fluctuations of Δ_∊ (hereinafter σ _{Δ ∊}) are largest near the ice-sheet surface, and decrease with increasing depth and density (Fig. 5a and b). The rate of decrease is steep at depths shallower than ~21–26 m compared with the rate at greater depths. Therefore, the σ _{Δ ∊} transition occurs in the depth range 21–26 m and density range ~580–620 kg m⁻³, as with the transition of the size of Δ_∊ over the same depth/density range. In the density range between ~820 and ~870 kg m⁻³, the gradient of σ _{Δ ∊} is steeper than that of shallower firn (Fig. 5).

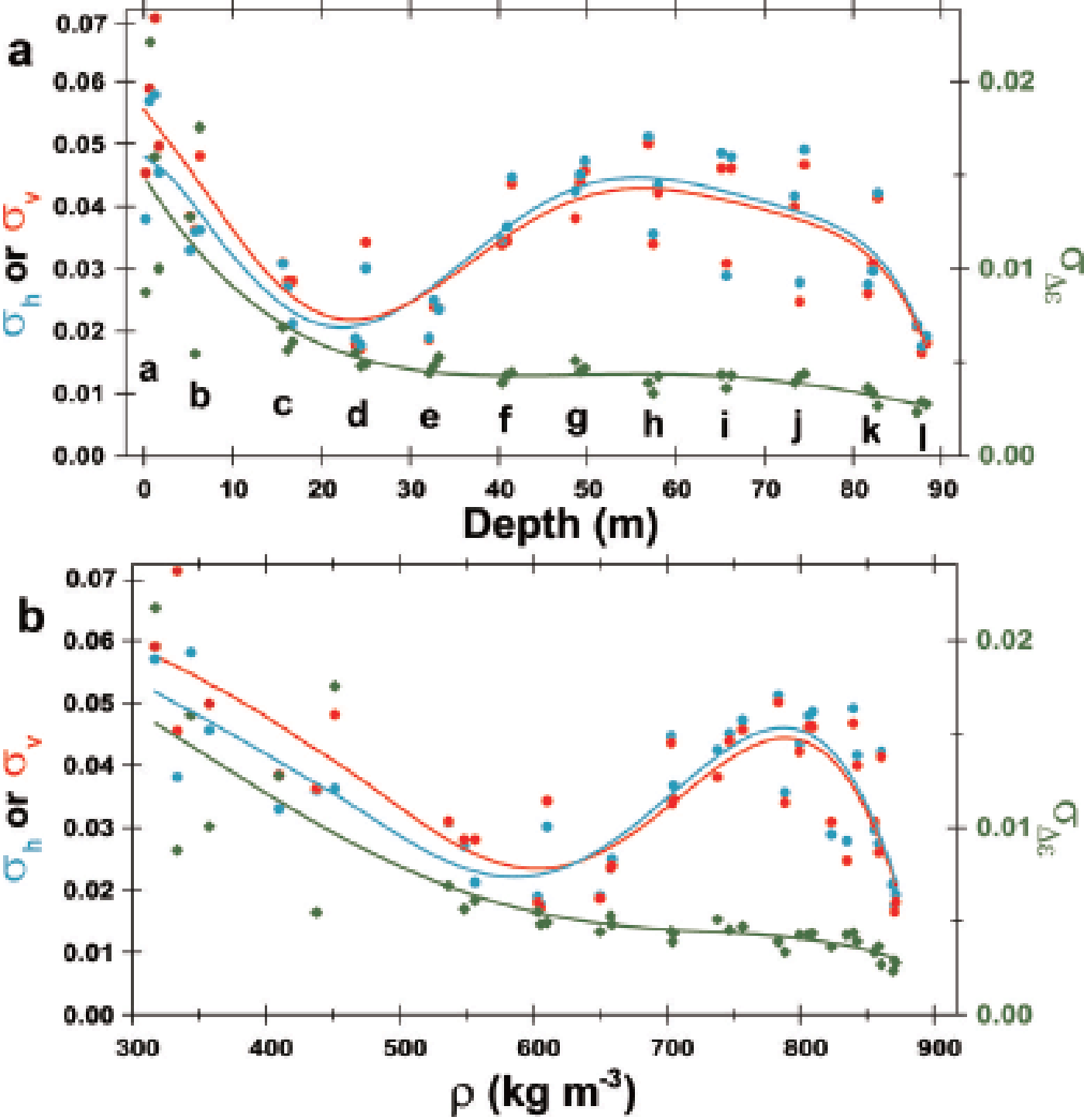
Fig. 5. Evolution of the standard deviations of the three components ∊_v, ∊_h and Δ_∊ with depth (a) and density (b) for the 37 pieces of 0.55 m long (or 0.50 m for the pit) core segments. The left axis indicates σ ∊_v or σ _h. These are the standard deviations of ∊_v (red) and ∊_h (blue), respectively. The right axis is σ _{Δ ∊} which is the standard deviation of Δ_∊ (green). The 12 depth ranges are indicated with letters a–l; σ ∊_v and σ _h have local minima at depths of ~21–26 m and at densities of 580–620 kg m⁻³, then have broad local maxima in the depth range 45–72 m and at densities of 740–830 kg m⁻³ if we use an arbitrary threshold, 0.04. In contrast, σ _{Δ ∊} decreases with increasing depth. The steep decreasing gradient changes into a less steep gradient at ~21–26 m depth and at densities of 580–620 kg m⁻³. At depths more than ~70 m and densities more than ~820 kg m⁻³, the gradient is again steeper.

The correlations show an evolution between Δ_∊ and permittivity components (∊_v and_h). The relations between Δ_∊ and_h are presented in Figure 6 as positive correlations at shallower depths, and negative correlations at greater depths. The distribution of data points in Figure 6 appears to ‘rotate’ in a counterclockwise direction with increasing depth, but the evolution shows a discontinuity in the density range 580–620 kg m⁻³; the left shallower side and the right deeper side of depth range ‘d’ have a contrasting distribution of data points. In addition, the transition from positive to negative correlation occurs in the density range ~580– 620 kg m⁻³. The evolution of the correlation is further shown in Figure 7 as the linear correlation coefficient r between Δ_∊ and ∊_h for the 37 pieces of the 0.55 or 0.50 m long samples. Only ∊_h is shown here, but ∊_v gives very similar correlations. Near the surface the correlation is positive (r ~ +0.5), and r decreases with increasing depth and density. It is zero in the depth range 21–26 m and at an average density of ~580– 620 kg m⁻³. In the depth range 50–80 m, r reaches a minimum of ~–0.5. The center of the broad minimum is ~50–80 m (Fig. 7a) at a density of ~750–850 kg m⁻³ (Fig. 7b) if we use an arbitrary threshold of –0.4. At greater depths with average density ~820–870 kg m⁻³, r again comes closer to zero. At a depth close to 90 m, where the average density is ~870 kg m⁻³, r is ~–0.3 (Fig. 7a and b). As shown below in Section 4 (Figs 9 and 10), these changing correlations are also shown with correlations against oxygen isotope ratio and various ions. The statistics of the measured values mentioned in this section are listed in the Appendix.

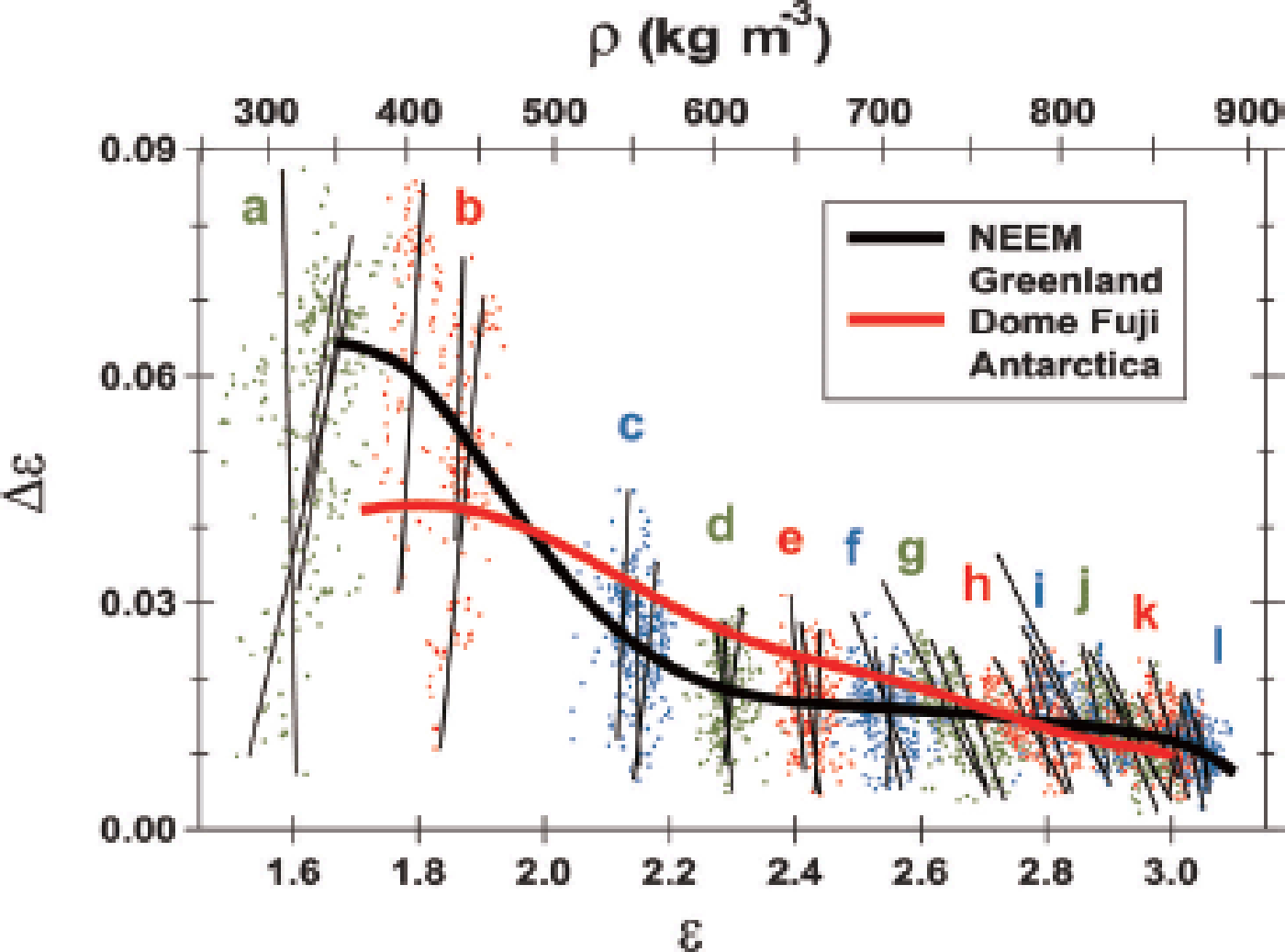
Fig. 6. Distribution of Δ_∊ vs ∊_h for all measured samples from the 12 depth ranges. Dots and letters with three different colors (green, red and blue) are used to discriminate between neighboring depth ranges. The lines are fitted every 0.55 m or 0.50 m. By using the empirical relation between ∊_h and density in Figure 4, a scale of density ρ is given as the top axis. In the shallow depth range of a and b, Δ_∊ and ∊_h have positive correlations. The correlations decrease and reach nearly zero in the depth range of c and d, and then become negative. The negative correlations are dominant at deeper ranges from e to l (Fig. 2), with minimum correlations near the firn-to-ice transition density (Fig. 7). The average tendency for all data is given as the black solid line. For comparison, the Δ_∊−∊_h relation for the Dome F station ice core (Fujita and others, 2009) is given as a red solid line. In the density range 470–700 kg m⁻³, the average Δ_∊ at Dome F is larger than the Δ_∊ of NEEM by up to 0.01 or ~50%. This result suggests more destruction of the anisotropic structure of ice and pore spaces at NEEM than at Dome F under the same density conditions.

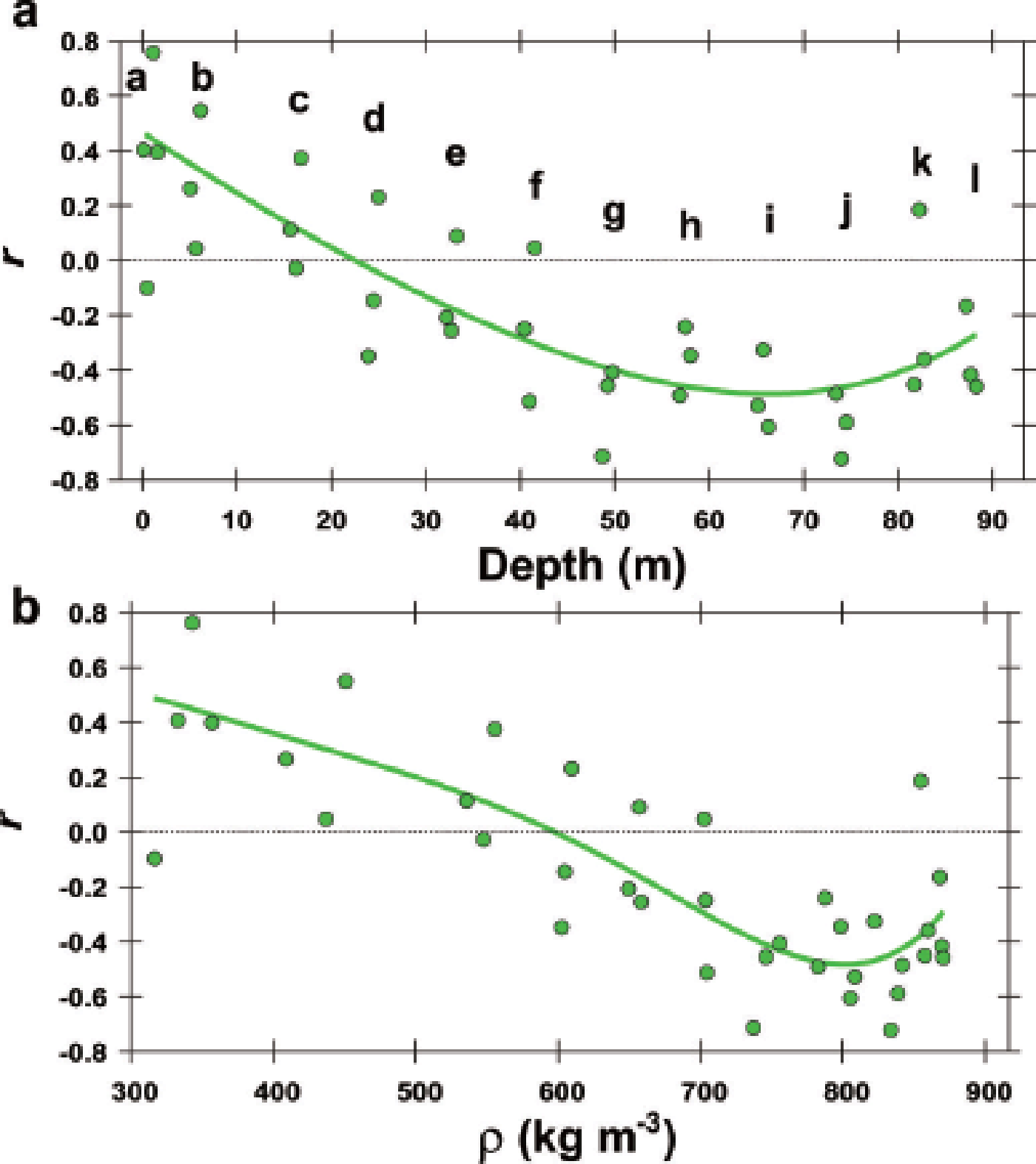
Fig. 7. Evolution of the linear correlation coefficient r between Δ_∊ and ∊_h vs depth (a) and density (b). Letters a–l are the depth ranges. The green symbols are r for the 37 pieces of 0.55 or 0.50 m long samples. The green lines show the mean tendency. The linear correlation coefficient r is ~0.5 at the surface, and r decreases to zero at depths of ~21–26 m and in the density range 580–620 kg m⁻³. Also, r is smallest at depths of 50–80 m and in the density range ~750–850 kg m⁻³ if we use the arbitrary threshold of –0.04. After this minimum, r approaches zero.

3.2. Impurities

Of the ion species investigated, we found that F⁻, Cl⁻, Ca²⁺, Mg²⁺, Na⁺ and NH₄ ⁺ are significantly correlated with the permittivity components. Correlations between these ions and the dielectric permittivities are given in Table 1. The statistics for the concentration of these ions are given in Table 2. The other species, including major ions SO₄ ^2– and NO₃ ⁻, had no significant correlations with the dielectric permittivities (Table 1), so these ions are not discussed in the rest of this paper. F⁻ and Ca²⁺ have a similar seasonal dependency, i.e. rich in winter to spring; Cl⁻, Na⁺ and Mg²⁺ have a common dependency, i.e. rich in winter; and NH₄ ⁺ is rich in summer. This seasonality has been shown in previous studies (e.g. Kuramoto and others, 2011). Linear correlation coefficients between these ions are given in Table 3, and suggest a close link between F⁻, Ca²⁺ and Mg²⁺ and between Cl⁻, Na⁺ and Mg²⁺, and independency of NH₄ ⁺.

Table 1. Linear correlation coefficients between concentration of major ions and deviatoric and Δ_∊ for firn from depth ranges h, i and j. Bold type indicates significant correlations (p < 0.001)

Table 2. Statistics for concentration of major ions (ppb) for firn from depth ranges h, i and j

Table 3. Correlation coefficient matrix for ion species for firn from depth ranges h, i and j. Bold type indicates significant correlations (p < 0.001)

4. Discussion

4.1. Initial state of layering near the surface

Here we discuss the initial state of layering near the surface, in terms of density, ∊_v, ∊_h, Δ, chemistry and their seasonality. We also include additional results from the 2 m pit study; the initial state essentially determines the nature of firn in terms of both physics and chemistry.

4.1.1. Initial state of density strata and their seasonality

Based on a 2 m deep pit study during the NEEM 2010 season, Kuramoto and others (2011) observed pronounced seasonal variations in the stable isotopes of water. These variations indicate that the snow had accumulated evenly during the 4 years of investigation. In addition to their data, we provide a detailed profile of δ¹⁸O, ρ,_h and Δ_∊ within the 2 m pit during the NEEM 2012 season in Figure 8a–c. Considering δ¹⁸O and ion concentrations (not shown), we deduce the seasons of deposition. Approximately three annual cycles occur within the 2 m pit (Fig. 8a). We find numerous density peaks and troughs with 3.3 mm resolution (Fig. 8b). That is, density peaks appear at any time during the annual cycles. Troughs tend to appear in summer, as we see at depths of ~0.1, ~0.7 and ~1.3 m. Winter peaks are not as sharp as summer peaks and troughs (e.g. at depths of 0.2–0.6, 0.8–1.2 and 1.7–2.0 m). These peaks imply that firn is more homogeneous in winter.

Fig. 8. Initial conditions of the layered firn in the shallowest 2 m pit on 2–3 July 2012. (a) δ¹⁸O profile (‰). An annual cycle has ~0.7 m of snow. The shallowest 0.21 m is the snow deposition in June 2012. (b) 3.3 mm resolution density profile measured with the gamma-ray transmission method. The density tends to be high and smoother in winter. Less-dense peaks appear in summer. (c) Dielectric permittivity profile, where ∊_h is the red line referring to the bottom axis. Δ_∊ is the green line referring to the top axis. Both have positive correlations. (d) Relations between deviatoric (deviation from the average tendency) (x –axis), Δ_∊ (y –axis) and δ¹⁸O (color scale z). Summer data points (red) are widely scattered within this plot. Winter data points (purple) tend to be distributed at the top right. (e) Relation between Δ_∊ (y –axis) and δ¹⁸O (x –axis). Summer data points reside within a wide range of Δ. Winter data points reside within a high range of Δ. (f) Relation between deviatoric (y –axis) and δ¹⁸O (x –axis). Winter data points reside within a high range of.

The initial state of the density strata and their seasonality have been studied for >50 years. Based on extensive stratigraphic studies of the snow and firn, including in the inland region of the Greenland ice sheet, Benson (1962) observed that stratigraphic discontinuity forms in late summer or autumn, with a coarse-grained, low-density layer often containing depth hoar overlaid with a finer, dense layer. Traditionally, depth-hoar formation in such a sequence has been linked to metamorphism during autumn in the seasonal temperature cycle. Summer-warmed snow loses vapor to colder overlying air. The vapor is redistributed by diffusion, convection and windpumping (e.g. Bader, 1939; Benson, 1962; Gow, 1968; Alley and others, 1990).

Higher density of snow in winter is explained by a wind-pack effect. This was also discussed for the firn at NEEM (Kuramoto and others, 2011) and at GISP2 (Albert and Shultz, 2002). In summary, density strata are essentially related to metamorphism in summer and autumn at NEEM, whereas they are related to wind packing in winter.

4.1.2. Initial state of Ɛ ∊_v, Ɛ_h and Δ^Ɛ and its seasonality

In Figure 8d–f, we further explore relations among δ¹⁸O, ρ,_h and Δ_∊ within the pit. Figure 8d shows relations between deviatoric (the deviation from the average tendency of evolution along the depth; x –axis), Δ_∊ (y –axis) and δ¹⁸O (z color scale). Deviatoric can be approximated as proportional to deviatoric ρ in a limited density range considering the proportionality between them (Fig. 4). Thus, we use deviatoric in discussions as a substitute for deviatoric ρ, without the need for resampling. In addition, δ¹⁸O values with a depth resolution of 30 mm were linearly interpolated to a depth resolution (5 mm) of the dielectric permittivity measurements. Summer data with higher δ¹⁸O (red in Fig. 8d) are widely distributed within this plot. The winter data (purple in Fig. 8d) tend to be distributed over a limited range at the top right. This observation indicates that winter layers are more homogeneous, whereas summer layers have high variability, as observed in the ρ data. Figure 8e and f give variations of Δ_∊ (y –axis) and deviatoric vs δ¹⁸O (x- axis), respectively. Summer data are distributed over a wide range on the y –axes. Winter data points occur within limited high ranges. Overall, high values of Δ_∊ (~0.06) can initially occur for deposition during any season (Fig. 8e). In denser firn (Fig. 8d), Δ_∊ tends to be high, because the initial snow density influences depth-hoar growth under a temperature gradient (Pfeffer and Mrugala, 2002). However, even when tends to be small in summer hoar formation, the summer firn layers have high Δ_∊ values (Fig. 8e and f). This initial state of ∊_v, ∊_h and Δ_∊ and the seasonality is established already within 0.2 m of the surface (Fig. 8c). This state is a starting point for further evolution of the layered deformation.

4.1.3. Initial state of chemical strata and its seasonality

Based on a pit study during the NEEM 2010 season, Kuramoto and others (2011) reported that concentrations of Na⁺, Cl⁻ and Mg²⁺, which largely originate from sea salt, peaked in winter to early spring, while Ca²⁺, which mainly originates from mineral dust, peaked in late winter to spring, slightly later than Na⁺, Cl⁻ and Mg²⁺. Mg²⁺ also originates from mineral dust (e.g. Whitlow and others, 1992). Our new pit data confirm the results of this report. Though Kuramoto and others (2011) did not report on F⁻, our pit study of 2012 and at deeper firn confirms that F⁻ peaks in winter to late spring, similar to Ca²⁺.

4.2. Evolution of density and the anisotropic structure within firn

We now observe how the initial layering evolves with increasing depth, in order to understand the relations between initial layering and the layered deformation within the firn. The three stages are discussed in detail.

4.2.1. Stage I: rearrangement of grains

An important mechanism in the initial densification of snow is the main structural rearrangement of grains caused by the snow load. Our Δ_∊ data show a rapid decrease at depths of 21–26 m, i.e. to densities of ~580–620 kg m⁻³ (Figs 3 and 4). This rapid decrease in Δ_∊ is most likely caused by the structural rearrangement of grains, which decreases the anisotropic structure of ice and pore spaces. The transitional depth range 21–26 m and the density range ~580–620 kg m⁻³ are the levels of the main physical processes for densification. Below a depth where closest packing of grains has already been attained, it has been proposed that pressure sintering, dislocation creep, recrystallization and fracture become the dominant densification mechanisms (e.g. Gow, 1975; Alley, 1988; Hondoh, 2000; Fujita and others, 2009; Kipfstuhl and others, 2009; Cuffey and Paterson, 2010; Lomonaco and others, 2011). The Δ_∊ data show only gradual decreases at this stage (Figs 3, 4 and 6) and imply that pore spaces decrease slowly. Thus, the data tend to agree with earlier interpretations, though the transition density from the closest packing to the next stage is often given as 550 kg m⁻³ in early papers, which often referred to the initial rearrangement stage as stage I and the second pressure-sintering and dislocation creep stage as stage II (Fig. 1). Hereinafter, we denote the depth range 21–26 m and the density range ~580–620 kg m⁻³ as ‘transition I–II’.

4.2.2. Transition from stage I to stage II

We observe transition I–II to see how these two stages exhibit both continuity and discontinuity. The sign of coefficient correlation r between ∊ and Δ∊ changes from positive to negative at the depth and density of transition I–II (Figs 6 and 7). In addition, standard deviations of the permittivities σ _h and σ _v have local minima there (Fig. 5). In Figures 6 and 9, we observe that layers that deform preferentially catch up with layers that deform less rapidly and thereby create local minima of σ _h and σ _v. In other words, density has ‘local convergence’ at the depth/density of transition I–II. Our study demonstrates how each layer component behaves during the local convergence of density, which has been referred to as ‘density crossover’ (Gerland and others, 1999; Freitag and others, 2004; Fujita and others, 2009; Hörhold and others, 2011). It is noteworthy that these studies commonly show the local convergence of density at a mean density within 600–650 kg m⁻³ (Hörhold and others, 2011). We suggest that the density of transition I–II is 580–650 kg m⁻³ for firn in polar ice sheets, rather than 550 kg m⁻³. In stage II, we observe that σ _h and σ _v increase and the deformed layer has larger ∊ and smaller Δ∊ due to destruction of the anisotropic structure of pore space and ice. This means that the layers are preferentially deformed. In stage II, the density profile oscillates cyclically between more deformed isotropic layers and less deformed layers with higher anisotropy, and thus shows negative correlations within the Δ∊ –∊ _h plot (Fig. 6). In Section 4.3, we investigate the dominant causes of the preferential deformation.

4.2.3. The local maxima of σ_h and σ_v and the local minimum of r

The major phenomena occurring in stage II are the local maxima of σ _h and σ _v and the local minimum of r. These are found in most depth/density ranges, centered at ~45–80 m depth (Fig. 7a) and ~750–850 kg m⁻³ average density (Figs 5 and 7). Earlier studies (e.g. Benson, 1962; Anderson and Benson, 1963; Maeno and Ebinuma, 1983; Cuffey and Paterson, 2010) argued that a ‘second critical density’ existed at 820–840 kg m⁻³, where the shrinkage of entrapped air bubbles starts, until the theoretical density of ice (917 kg m⁻³) is attained. This later stage was sometimes referred to as stage III in earlier studies (Fig. 1), though further stages were proposed by some authors. At a density of ~830 kg m⁻³, air bubbles are closed within the ice matrix (e.g. Cuffey and Paterson, 2010). Our local maxima of σ _h and σ _v and the local minimum of r occur in a much broader density/depth range without a sharp peak or discontinuous changes. The main difference between this earlier study (sharply defined critical density) and the present study (much broader density/depth range) is that the former observed the phenomena only with density averaged over a large depth range, whereas our observations were performed in mm to cm resolution. Therefore, to better understand the relatively broad transition between stages II and III, we argue that it is essential to see the layered conditions with the mm- to cm-scale high-resolution data. Hereinafter, we refer to the relatively wide depth/density range of our local maxima of σ _h and σ _v and the local minimum of r as ‘transition II–III’. The definition is based on the sizes of σ _h, σ _v, the size of density fluctuations σ_ρ , or r.

4.2.4. Transition from stage II to stage III: layered closing of air bubbles

We explain the transition II–III as follows. The transition is reached when the deformation rate of the less deformed layers starts to catch up with that of the preferentially deformed layers. At that time, the density contrast between them is largest. When the firn density approaches the pore-closing density 830 kg m⁻³, the firn has less pore space left for further deformation. Such conditions are reached preferentially in ‘more deformed’ layers. In the layered condition, this process grows only gradually. With increasing depth, higher proportions of layers reach bubble-closing conditions, until the least deformed layers also reach bubble-closing conditions. Thus, transition II–III is a wide zone similar to the ‘lock-in zone’ defined in a study of gas transport within firn (Sowers and others, 1992).

In stage III, we observe that Δ∊ becomes smaller than before along the depth (Fig. 3) and along the density (Fig. 4). In addition, r starts to approach zero (Fig. 7). Moreover, σ _h and σ _v rapidly decrease (Figs 5 and 7). The most plausible explanation for this series of phenomena is that shrinking air bubbles have less volume, so the pore space geometry has less effect on the dielectric permittivities. In summary, we confirm that transition II–III is the transition from open-pore shrinkage to the shrinkage of closed air bubbles in the layers.

4.3. Correlations between deformation, impurities and seasons

Based on the discussions in Section 4.2, causal chains from the initial layering to stages I, II and III are not yet clear. For better understanding, we must investigate correlations among deformation, impurities and seasons.

4.3.1. Empirical correlations

As we saw in Section 3.2 and Tables 1 and 2, ions F⁻, Ca²⁺, Mg²⁺, Cl⁻, Na⁺ and NH₄ ⁺ correlate with the permittivity components. The correlations of F⁻ with the permittivity components are as large as those of Ca²⁺, in spite of F⁻ existing in very small concentrations compared with those of Ca²⁺. Earlier studies (Hörhold and others, 2012; Freitag and others, 2013) reported that, in firn cores in Greenland and in firn cores at some East Antarctic coastal sites with relatively low elevation (<~3000 m), a strong positive correlation exists between the density and the logarithm of Ca²⁺ concentration. As shown in the present study, several other major ions have significant correlations with the amount of deformation. We then hypothesize that one or multiple ions have physical links with layered deformation. Considering earlier studies, we suggest that the possible causes include F⁻, Cl⁻ and possibly NH₄ ⁺, and not cations such as Na⁺, Ca²⁺ or Mg²⁺ for the reasons discussed below.

In Figure 9, we show how δ¹⁸O, F⁻, Ca²⁺ and Cl⁻ change their distributions during the evolution of the Δ∊ –∊ _h relation. Again, to compare the 25–40 mm resolution data of δ¹⁸O and ions with the 5 mm resolution data of the dielectric permittivity measurements, the former data were linearly interpolated. In Figure 9, deviatoric ∊ _h on the x –axis is an indicator of deformation, Δ∊ on the y –axis is an indicator of structural anisotropy, and z values are expressed with a rainbow color scale. For all δ¹⁸O, F⁻, Ca²⁺ and Cl⁻, we do not find a clearly localized distribution within the Δ∊−∊ _h plot in the shallowest data (panels a-1–d-1). However, the localized distribution is developed as we go deeper (a-2–d-2 and a-3–d-3). Finally, the localized distribution is very clear in the depth/density range of transition II–III (a-4–d-4). Preferentially deformed layers have smaller values of δ¹⁸O, and thus are probably ‘non-summer’ layers. Less deformed layers tend to be summer layers with larger values of δ¹⁸O. Panels b-4 and c-4 demonstrate that portions with more F⁻ and more Ca²⁺ deform preferentially. Panel d-4 shows that portions with more Cl⁻ also deform preferentially. Examples of Mg²⁺ (not shown) are very similar to F⁻ and Ca²⁺. Na⁺-rich portions behave very similarly to Cl⁻ because the origin of these ions is commonly sea salt. NH₄ ⁺ (not shown) also has a significant correlation with deformation (Table 1). Panels a-2–d-2 and a-3–d-3 reveal transitional conditions toward the very localized distribution exhibited in panels a-4–d-4. Even in stage I, where the dominant densification mechanism is the rearrangement of grains, this transition is visible. Therefore, the transitions are commonly present in stages I and II.

Fig. 9. To investigate possble causes of the preferential densification and deformation, ‘Δ∊ vs deviatoric ∊ _h’ plots for four depth ranges (columns of the panels) are given with four kinds of information in the panel rows: δ¹⁸O, concentrations of ions F⁻, Ca²⁺ and Cl⁻. In all, 16 panels (4 depth ranges × 4 kinds of z scales) are given. The color scale for z is given at the bottom. Values for the top color (red) and bottom color (purple) are given in the boxes in the far left column. Ion concentrations are in a logarithmic scale under the assumption that deformation is most likely related to the logarithm of the ionic concentrations (e.g. Jones, 1967). The lines in each panel are fitted lines for each 0.55 m (or 0.50 m) at depths shallower than 33.5 m and for each 1.65 m for depths greater than 56.7 m. (a-1–a-4) Firn with smaller (larger) d18O tends to deform more (less) toward the deep (h, i and j) samples. (b-1–b-4) Firn with a larger (smaller) concentration of F– tends to deform more (less) toward the deep (h, i and j) samples. (c-1–c-4) Firn with a larger (smaller) concentration of Ca²⁺ tends to deform more (less) toward the deep (h, i and j) samples. (d-1–d-4) The concentration of Cl– is also correlated with deformation. (a-2–d-2) and (a-3–d-3) are transitional conditions between (a-1–d-1) and (a-4–d-4).

To see both possible textural effects initially formed by the seasonal variation of metamorphism and possible seasonal effects of impurities, we are very interested in correlations between the seasons of deposition and preferential deformation. In Figure 10, we provide the distribution of the first derivative of δ¹⁸O along the depth (y –axis) vs δ¹⁸O (x –axis) for the 4.95 m long core data from 56.7 m to 74.8 m (depth ranges h, i and j). The circular distribution of data points is related to the season of deposition, as schematically shown at the top right. The z properties of each data point are shown as rainbow color scales. They include deviatoric ∊ (Fig. 10a-1) and Δ∊ (Fig. 10a-2) as indicators of the preferential deformation. The z properties are also shown for the concentrations of F⁻, Ca²⁺, Cl⁻ and NH₄ ⁺ on a logarithmic scale (Fig. 10b–e). Preferential deformation occurs mostly between late autumn and the subsequent early summer (Fig. 10a-1 and a-2). In other words, less deformation occurs between midsummer and early autumn. Ions F⁻, Ca²⁺ and Mg²⁺ are rich between late autumn and early summer (e.g. Fig. 10b and c). The seasonal pattern is therefore similar to deviatoric ∊ (Fig. 10a-1) and Δ∊ (Fig. 10a-2). However, Ca²⁺ (Fig. 10c) and Mg²⁺ (not shown) ions are not necessarily rich in late autumn. Cl⁻ (Fig. 10d) and Na⁺ (not shown) are rich between autumn and spring. NH₄ ⁺ is rich between spring and winter (Fig. 10e).

Fig. 10. Seasonal characteristics of the deformation and related conditions for the 4.95 m long data at depths from 57 to 75 m (depth ranges h, i and j). In six panels, plots are common distributions of the first derivative of δ¹⁸O along the depth (y –axis) vs δ¹⁸O (x –axis), but with different z (color scale) properties. The season of each data point can be observed, since the circular distribution of dots is related to the deposition season, as schematically shown in the top right corner. In the top row, z properties are deviatoric ∊ (a-1) and Δ∊ (a-2). They are related to the amount of deformation. Red, green and yellow dots represent more-deformed firn, and purple and blue dots less-deformed firn. Note that the color scale for Δ∊ is reversed to show more destruction as red, green and yellow. In the bottom row, z properties are concentrations of F⁻, Ca²⁺, Cl⁻ and NH₄ ⁺ on the logarithmic scale (b–e). F⁻, Ca²⁺ and Cl⁻ have similar seasonal distributions. The seasonal distribution of NH₄ ⁺ differs from that of the other ions.

Based on the data, we contend that no single component strongly enhances preferential deformation. Nevertheless, some ions, namely, F⁻, Ca²⁺ and Mg²⁺, tend to enhance deformation between winter and summer, with large correlation coefficients (Table 1). Cl⁻ and Na⁺ tend to agree with deformation between autumn and spring, also with large correlation coefficients. Empirically, the concentration of NH₄ ⁺ is negatively correlated with deformation. The snow in less deformed layers is deposited between midsummer and early autumn.

4.3.2. Physical link between deformation and impurities

Tables 1 and 2 give the correlation coefficients between major-ion concentrations and deviatoric ∊ and Δ∊ (Table 1) and statistics for concentrations of major ions (Table 2) for NEEM firn sections h, i and j. As shown in Table 1, correlation coefficients are reasonably high for six of the eight ions analyzed in this study. Ion concentrations range from sub-ppb levels (F⁻, Ca²⁺, Mg²⁺ and Na⁺) to >200 ppb (SO₄ ^2–). Below we discuss three ions (F⁻, Cl⁻ and NH₄ ⁺) that can be compared and referred to data currently available from published work.

In experiments with single ice crystals, Nakamura and Jones (1970), Jones and Glen (1969) and Jones (1967) found that the addition of HF and HCl at a 10⁴–10¹ ppb level could increase ice deformation rates dramatically because of softening of the ice crystals by substituting F⁻ or Cl⁻ ions at locations of O in the crystal lattice of hexagonal ice. These substitutions create a number of point defects in ice and thus facilitate the movement of dislocations (Jones, 1967; Jones and Glen, 1969; Nakamura and Jones, 1970). In contrast, doping NH₄OH can cause point defects in the ice lattice and produce a small hardening (Jones and Glen, 1969). Petrenko and Whitworth (1999) and Fletcher (1970) reviewed and summarized those findings.

Based on Jones and Glen (1969), the addition of 30 ppb of HF could double the deformation rate (a softening effect) at –70°C. Assuming the HF effect on deformation rate is linear, effects of F⁻ ions found in this study, ranging from 0.03 to 2.38 ppb, would then increase deformation rates several percent. Similarly, for the case of Cl⁻, based on Nakamura and Jones (1970) an addition of ~2700 ppb HCl could increase deformation rates by a factor of ~5 at –26°C; another several percent of deformation rate increase, due to the Cl⁻ ions ranging from 1.50 to 77.3 ppb, could be calculated, again assuming Cl⁻ effect on deformation rate is linear.

For NH₄ ⁺, Jones and Glen (1969) found opposite deformation effects compared to those for F⁻ and Cl⁻. They found the deformation rate decreased by ~40% with the addition of ~5000 ppb NH₄ ⁺ in their experiment samples at –70°C. Taking its linear proportion again, the maximum NH₄ ⁺ concentration of ~90 ppb found in the three firn sections would generate hardening, but the effect was <1%.

These evaluations are approximate, because of the complexity of deformation effects by ions and lack of data on the activation energy of ice deformation, as well as the difficulty of precisely measuring dissolved ion concentrations (speciation measurements). In addition, the measurements are for single crystals whereas polar firn is a polycrystalline material. Meanwhile, strain rates used in the earlier laboratory experiments presented above are >10³ times faster than those ongoing within the firn at NEEM (Fig. 11; Section 4.5). However, the aforementioned rough estimation can provide basic information on those ions’ effect on firn deformation. In summary, F⁻and Cl⁻ ions in the NEEM firn can increase firn deformation rates on the order of several percent or more respectively, while NH₄ ⁺ can decrease deformation rates presumably by <1%. Therefore, we argue that F⁻ and Cl⁻ indeed caused a major part of the preferential deformation and that NH₄ ⁺ also contributed significantly.

4.3.3. Superficial deformation–calcium correlations without physical link

Cations Ca²⁺, Na⁺ and Mg²⁺ were also correlated with deformation. However, no reliable physical causality was found to be based on these cations. Table 3 shows that the correlation between Cl⁻ and Na⁺ is close to 1. If Cl⁻ softens ice, the deformation can be superficially correlated with Na⁺ even if Na⁺ itself has no impact on preferential deformation. Thus, it is reasonable to reject Na⁺ as a possible cause. Similarly, Ca²⁺ and Mg²⁺ are well correlated with F⁻ and/or Cl⁻ (Table 3). This provides a possible explanation of why both Ca²⁺ and Mg²⁺ are only superficially correlated with deformation without a real physical link. Indeed, in our ongoing research on firn cores at Dome F we performed a study with very similar analyses and procedures. We found no correlation between the Ca²⁺ concentration profile and the density profile in stage II.

Understanding the forms of impurity ions within firn is also very important. In the Greenland Ice Core Project (GRIP), Iizuka and others (2008) examined the various forms of chemical compounds of the Holocene ice of the GRIP ice core, based on analysis of the ion balance. They estimated that Ca²⁺ ions are present mostly as calcium sulfate and calcium nitrate as solid particles. Sakurai and others (2009) showed that calcium sulfate salts are present as micro-inclusions in the GRIP ice core. The compounds are detected by two independent methods: micro-Raman spectroscopy of a solid ice sample, and energy-dispersive X-ray spectroscopy (EDS) of individual inclusions. They also identified magnesium sulfate and/or sodium sulfate as solid particles. This fact implies that these particles have no correlation with deformation as dissolved Ca²⁺. Since Ca²⁺ ions are present in solid particles, it is unlikely that Ca²⁺ can interfere with the density of point defects within the ice lattice. We comment here that sulfate and nitrate have no significant correlation with densification (Table 1), which implies that these particles have nothing to do with deformation. More recently, using EDS, Lomonaco and others (2011) showed that impurities exist in the GISP2 firn core in two forms: soluble impurities and dust-like particles. They found F⁻ and Cl⁻ within soluble impurities, and Ca²⁺ within dust-like impurities. Most micro-inclusions were found within a grain interior rather than grain boundaries. In addition, no reliable evidence suggests that dust particles significantly soften ice. Rather, it is natural to think that dusts impede dislocation motion.

In Section 4.4, we suggest that the deposition of late summer to autumn is hardened by insolation-based meta-morphism, i.e. the opposite of softening. In this season, concentrations of Ca²⁺ and Mg²⁺ are very low. Therefore, we hypothesize that this seasonality of ions increases the presumed superficially high correlations between Ca²⁺ ions and deformation.

As pointed out in Section 4.3.1, we observe that Ca²⁺ ions are in transition toward a very localized distribution (Fig. 9c-2). In stage I, where the dominant densification mechanism is the rearrangement of grains, this transition already occurs. A very similar condition is observed in other Greenland firn: Hörhold and others (2012) showed that the correlation between Ca²⁺ and densification developed rapidly in their Greenland B29 site firn (their Fig. 3). This observation means that Ca²⁺ is correlated with the rearrangement of grains. It seems that these correlations cannot be reliably explained by a real physical link. First, this rapid development of correlation has nothing to do with dislocation creep nor pressure sintering because stage I does not yet occur for these mechanisms. Second, Ca²⁺ cannot enhance the rearrangement of grains because it occurs mostly in the grain interior. Even an alternative assumption that grain boundary slip is enhanced due to the presence of more impurities is highly unlikely since we find no supporting data for the enhancement of grain boundary slip. Possible causes for the rapid development of the correlation between Ca²⁺ and densification are discussed in the next subsection.

4.4. The textural effects on mechanical properties of firn caused by summer-to-autumn metamorphism

In addition to the proposed physical link between deformation and impurities such as F⁻, Cl⁻ and NH₄ ⁺, we propose another key to understanding firn mechanical properties: the textural effects caused by summer-to-autumn metamorphism. From Section 4.1.1, metamorphism of firn related to solar heating occurs at the ice-sheet surface within the deposition of late summer to early autumn. Curiously, this portion experiences least deformation and shows the least concentration of F⁻ and Cl⁻ ions but the largest amount of NH₄ ⁺, as discussed above. Therefore, we need to be careful not to mix or misjudge the effects of these ions and the possible textural effects caused by summer-to-autumn meta-morphism.

The essential part of the proposed textural effect is more development of mechanical strength due to (1) ice grain– grain bonding, (2) c –axis cluster around the vertical axis and (3) anisotropic geometry of ice and pore. These processes are assumed to work interdependently during a series of densification stages (Fujita and others, 2009). Winter layers are proposed to be locations that do not receive direct heat from the sun; only vapor molecule movement through them occurs in all seasons, attaining only weaker strength. In the previous subsection, we saw rapid development of the correlation between Ca²⁺ and densification in stage I. In light of the proposed textural effect, Ca²⁺-rich portions are winter layers; thus, the above fact is explained.

We further examine the data at NEEM in terms of the textural effects. At NEEM, within several meters of the ice-sheet surface, less-dense layers of the summer depth hoar occur (Fig. 8). These layers are apparently fragile. We observed in our unpublished 5 m deep pit data at NEEM that rapid destruction of the summer depth hoar occurs at depths of several meters. Thus, the present study implies that the summer strata that contain fragile portions at the initial rearrangement stage I are indeed the hardest portions during the deeper part of stages I and II. This inference seems contradictory at first glance. Our question is whether the summer-to-autumn metamorphism can really harden firn during stages I and II.

The key lies in the initial snow properties. We cite here Benson’s (1962) description of snow properties in Greenland. ‘Summer strata are generally coarser-grained and have lower density and hardness values than winter layers; they may also show evidence of surface melt. Also, there is usually more variability in summer layers, with coarse-grained, loose layers alternating with finer-grained, higher-density layers or even wind slabs of variable thickness. Winter layers are generally more homogeneous, with higher density and finer grain size than summer layers.’ Alley (1988) made essentially the same observation. These observations apply to the NEEM case considering features of the strata in Figure 8. Therefore, firn properties in summer and winter strata are very different. As at Dome F, winter layers have no chance to receive direct solar heat. Summer layers receive direct solar heat to attain high variability. They contain weak layers of depth hoar but they still contain higher-density layers. We hypothesize that this layered structure, formed in summer, as a whole makes the summer layers harder than the more homogeneous winter layers during both stages I and II. Rapid destruction of winter layers in stage I (Fig. 9a-2–d-2, and the Greenland B29 site firn case discussed above) is taken as supporting evidence. In addition, the summer-to-autumn layers contain summer formed vapor that is redistributed by diffusion, convection and windpumping (e.g. Bader, 1939; Benson, 1962; Gow, 1968; Alley and others, 1990). Higher-density layers within the summer-to-autumn layers can be harder due to the proposed textural effects. Indeed, the initial fabric measured in the firn from 33 m depth downwards is clustered around the vertical axis and cannot be explained by the level of strain reached at these depths (Montagnat and others, 2014). Another piece of circumstantial evidence is the fact that the O₂/N₂ ratio at the GISP2 site is correlated with local summer insolation (Suwa and Bender, 2008). Without the presence of the insolation-based summer-to-autumn metamorphism effect, this fact cannot be explained. We attempted a multiple regression analysis to explain deviatoric ∊ and Δ∊ by concentrations of F⁻, Cl⁻ and NH₄ ⁺. We found that only 52% and 21% of the deviatoric ∊ and Δ∊, respectively, could be explained by the linearly superposed effects of these ions. We hypothesize that the remaining proportions are closely associated with the proposed textural effects.

4.5. A schematic picture for evolution of the firn at NEEM

We summarize here the evolution of the firn at NEEM, because the entire picture becomes clearer after the above discussions. We come back to Figure 1, which is a schematic representation of the evolution of density and permittivity with increasing depth, based on the data and discussions of the present study. Also, evolution of the vertical strain rates within stages II and III is analyzed from the data and demonstrated in Figure 11. Initial strata are formed based on the deposition and the metamorphism soon after deposition. The largest values of Δ∊ are established within 0.2 m of the surface. This condition is similar to an observation that the degree of the ice/pore anisotropy develops rapidly within meters of the surface at GISP2 (fig. 5d in Lomonaco and others, 2011). Within meters of the surface, the upper limit of the density fluctuations is deposition from all seasons, with a weak bias from winter homogeneously dense layers due to wind packing. The lower limit near the surface tends to be summer depth hoar. All of these layers experience the initial processes of rearrangement and destruction until the convergence of density fluctuations at transition I–II. During stage I, initial snow densities are almost doubled on average. The homogeneous winter layers generally become denser rapidly, with limited summer hoar layers. These phenomena cause the superficial correlations between densification and, already during stage I, some ions (e.g. Ca²⁺).

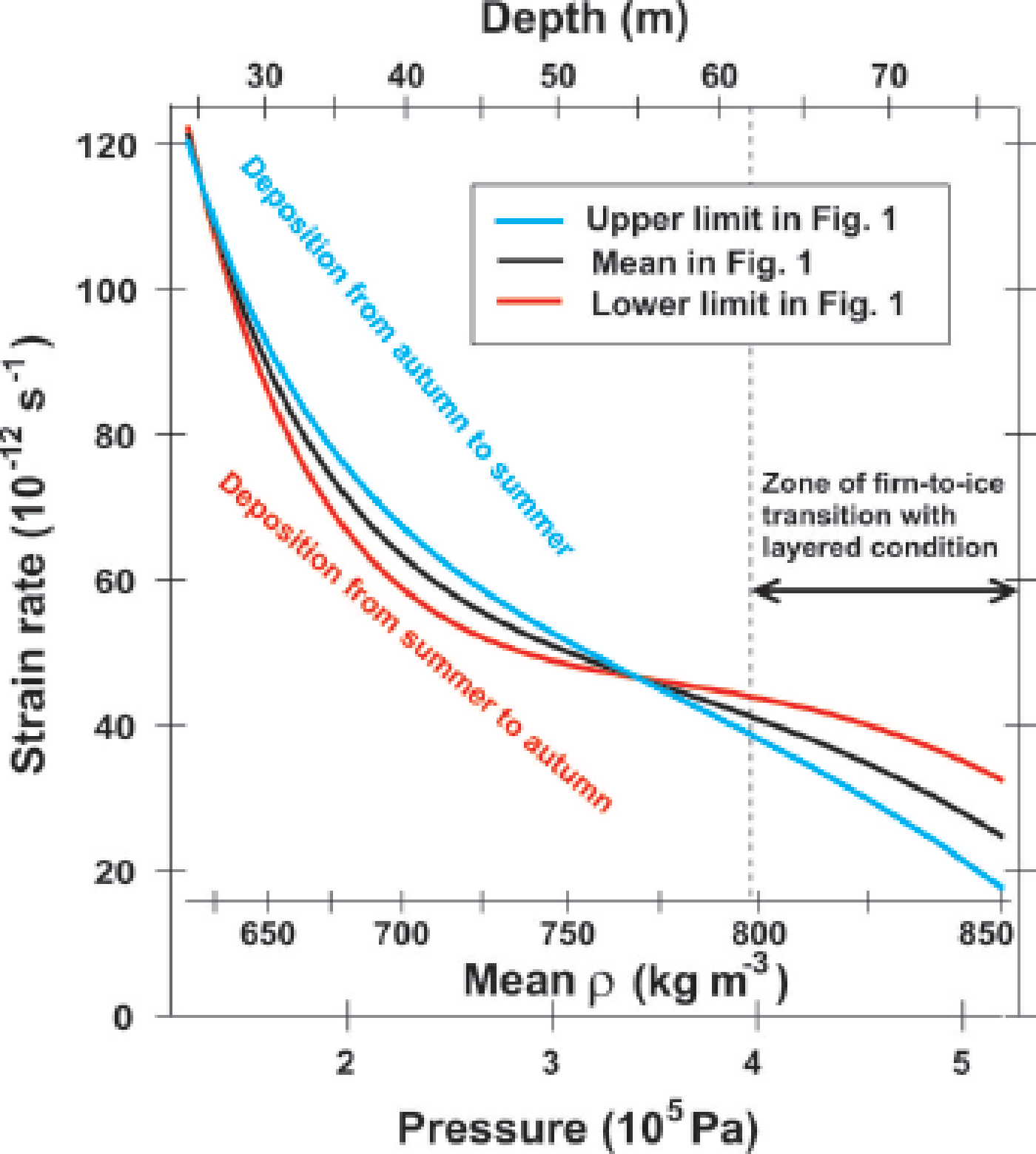
Fig. 11. Evolution of the vertical strain rate in stages II and III within the NEEM firn. The three x –axes are pressure (bottom axis), mean density (second-bottom axis) and depth (top axis). The y –axis indicates the vertical strain rate. The blue and red lines are derived from the ‘upper limit’ and ‘lower limit’ profiles in Figure 1, respectively. The black line is the mean profile of Figure 1. At the convergence of the density at 20–25 m, the vertical strain rate is ~1.2 × 10⁻¹⁰ s⁻¹. The ‘upper limit’ deforms faster than the ‘lower limit’ by up to ~15% because it is softer. The strain-rate crossover is found at ~55 m depth and at a mean density of ~770 kg m⁻³. The vertical strain rate is then 4.7 × 10⁻¹¹ s⁻¹. In the firn-to-ice transition zone, strain rates of the ‘lower limit’ layers are much larger than those of the ‘upper limit’ layers because they have more remaining pore spaces that can deform further. This condition occurs because the ‘lower limit’ is harder and continues to deform for a longer time period.

At transition I–II, the vertical strain rate is ~1.2 × 10⁻¹⁰ s⁻¹ (Fig. 11). At stage II, the upper limit tends to be deposition from autumn to the subsequent summer, with higher concentrations of F⁻, Cl⁻ and other ions. The lower limit in the greater depth range tends to be deposition from summer to autumn with higher concentrations of NH₄ ⁺. These portions experience summer-to-autumn metamorphism. The upper limit deforms faster than the lower limit by as much as ~15% (Fig. 11). We contend that the enhancement of deformation is in good agreement with the amount expected from F⁻, Cl⁻ and NH₄ ⁺. We suggest that this contrast of the deformational rate is caused partially by impurities (F⁻, Cl⁻ and NH₄ ⁺) and partially by textural effects. In the lower-limit layers, our Δ∊ data suggest large anisotropy in the ice/pore geometry. Quantitatively, Δ∊ ~ 0.025 means that the correlation length (Vallese and Kong, 1981) of the pore space along the vertical and along the horizontal (l _v and l _h, respectively) has an axial ratio of ~1.3 (fig. 7 in Fujita and others, 2009). In the upper-limit layers, our data of Δ∊ ~ 0.01 suggest low anisotropy in the ice/pore geometry. Δ∊ ~ 0.01 itself is explained by the cluster of crystal orientations around the vertical (fig. 7 in Fujita and others, 2009). We note that at GISP2, ‘fine-grained layers’ that originate in winter deposition have nearly zero ice/pore anisotropy at ~50 m depth (Lomonaco and others, 2011). Their data are in good agreement with ours for layers where Δ∊ is small (lower values of Δ∊ in Figs 2, 3 and 5). If coarse-grained layers of the GISP2 firn were investigated, we would expect to find large anisotropy in the ice/pore geometry. In Figure 1, the upper-limit profile (blue) and lower-limit profile (red) cross the firn/ice transition density (ρ = 830 kg m⁻³ or ∊ _h = 2.91) at 62 and 78 m, respectively. Between these depths, layers with closed bubbles and layers with open pore spaces coexist in the same depth range as the layered condition, and form the so-called lock-in zone. The crossover of the strain rate is found at ~55 m depth and a mean density of ~770 kg m⁻³ (Fig. 11). The vertical strain rate is 4.7 × 10⁻¹¹ s⁻¹. In a firn-to-ice transition zone, strain rates of the ‘lower-limit layers’ are much larger than those of the ‘upper-limit layers’ to reduce density fluctuation (Fig. 11).

Based on this picture, we suggest that enhanced deformation of late-autumn to subsequent early-summer layers is one of the factors that determine the start of the layered firn/ice transition. The hardness of midsummer-to-early-autumn layers determines the final depth of the layered firn/ice transition. In this way, summer-to-autumn metamorphism can play a dominant role in determining the duration of the firn-to-ice transition to modulate ice-core gas results (e.g. the O₂/N₂ ratio and TAC).

We note that the present discussions for NEEM cannot be immediately applied to other sites (e.g. the East Antarctic plateau) without performing a detailed comparison between firn conditions. The temperature range, accumulation rate, strain rate, amount and seasonality of ions are different. For example, at transition I–II, Δ∊ of Dome F firn is larger than that of NEEM by 0.01 or ~50% (Fig. 6). In addition, the decrease of Δ∊ vs density and depth at Dome F is more gradual and smoother (see figs 3 and 4 in Fujita and others, 2009). These facts mean that the anisotropy of ice and pore spaces is larger and preserved persistently for a much longer period of time at Dome F during stages I and II. Further, the insolation-based metamorphism plays a dominant role in Dome F firn. This topic must be developed elsewhere in detail to highlight the common and different processes among major ice-coring sites.

4.6. Meaning of dielectric anisotropy Δ∊ of the firn at NEEM

Finally, we review both the meaning and behavior of Δ∊ in the NEEM firn. Δ∊ is primarily a substitute for the anisotropic geometry of ice and pore space. In principle, Δ∊ does not contain information on ice–ice bonding. Information on ice– ice bonding must be extracted by two- or three-dimensional imaging methods or by mechanical tests. Δ∊ shows annual oscillations both near the ice-sheet surface (Fig. 8c) and in stage II (Fig. 10a-2). In layers from late autumn to the next early summer, Δ∊ is high near the surface (Figs 8c–e and 9a-1) but it rapidly drops toward ~0.01 during densification stages I and II (Fig. 9). Δ∊ clearly demonstrates the fragility and more deformable conditions of late-autumn to early-summer layers. Isotropic pore-space geometry means that vertical diffusion of the air through pore spaces is less active in these layers. In contrast, in layers from midsummer to early autumn, Δ∊ ranges widely between ~0.01 and ~0.07 near the ice-sheet surface (Figs 8c–e and 9a-1), but it drops only slowly toward ~0.02 during densification stages I and II (Fig. 9). In this case, Δ∊ clearly demonstrates persistently less deformable conditions of the summer-to-autumn layers. Anisotropic pore-space geometry means that in these layers, vertical diffusion of the air through pore spaces is more active. The persistently less deformable nature of the summer-to-autumn layers is similar to that of the firn at Dome F (Fig. 6). The two contrasting natures of Δ∊ in two different seasons in the annual cycle at NEEM indicate a crossover of tracks of Δ∊ within the Δ∊ –∊ _h plot in Figure 6 (not drawn in the figure). We suggest that in the Dome F firn, no major crossover of tracks of Δ∊ occurs within the Δ∊ –∊ _h plot because Dome F summer layers have higher Δ∊ and ∊ _h during stages I and II (Fujita and others, 2009).

5. Concluding Remarks

Evolution of the density and the anisotropic structure of ice and pore space in the layered firn at NEEM was investigated based on the dielectric permittivity components of the firn core. We suggest that layered deformation is explained by the present framework of ice physics. Ions such as F⁻, Cl⁻ and NH₄ ⁺ create a number of point defects in ice that facilitate the movement of dislocations. In addition, we suggest that the textural effects due to the summer-to-autumn metamorphism effects are also dominantly present in the firn at NEEM, as proposed for Dome F. In agreement with previous authors, we hypothesize that calcium is not the active agent in the reported deformation–calcium correlations. We hypothesize that high correlations between Ca²⁺ ions (and Mg²⁺ and Na⁺) and deformation are superficially caused by the seasonal synchronicity with cycles of F⁻, Cl⁻, NH₄ ⁺ and the summer-to-autumn meta-morphism. These processes, metamorphism and impurities, modulate the duration of the firn-to-ice transition and thus the O₂/N₂ ratio and the TAC in the trapped gas. To better understand the mechanisms and causal chains, future investigations need to focus on properties of the layered condition (e.g. summer and non-summer layers) of the firn. Furthermore, the relative roles of the two mechanisms, metamorphism and impurities, must be investigated in detail for major Greenland ice-core sites and major Antarctic ice-core sites. The dielectric permittivity tensor method is a useful tool to observe the evolution of the firn structure.