The Effect of Crystal Size and Dispersed-Solid Inclusions on the Activation Energy for Creep of Ice

Abstract

Steady-state creep-rates of polycrystalline ice were investigated as a function of temperature, grain-size, and inclusion concentration through uniaxial compression in the laboratory. Samples were run at a constant load with the temperature systematically varied between about —5^°C and —40^°C. The presence of inclusions inhibits dynamic recrystallization and grain growth; the average crystal size produced by recrystallization is inversely proportional to the inclusion concentration. At temperatures above —8^°C, creep-rate is enhanced by about a factor of two. This appears to be the result of the combined effects of recrystallization with accompanying grain growth and grain-boundary sliding. Over the temperature range —10^°C to —40^°C, the apparent activation energy for creep increases with increasing volume fraction of inclusions. This is apparently due to a thermally activated process which is modified by internal stresses created by the inclusions.

Résumé

Les effets de la dimension des cristaux et des inclusions solides éparses sur l’énergie d’activation pour le fluage de la glace. On a recherché en laboratoire par compression uniaxiale, les vitesses d’équilibre pour le fluage de la glace polycrystalline en fonction de la température, de la taille des grains et de la concentration en inclusion. Des échantillons furent soumis à des charges constantes avec des températures variant systématiquement entre — 5^°C et — 40^°C. La présence d’inclusions gêne la recristallisation dynamique et le grossissement des grains; la dimension moyenne des grains issus de recristallisation est inversement proportionnelle à la teneur en inclusions. Aux températures supérieures à — 8^°C, la vitesse de fluage est réduite d’environ un facteur 2. Ceci semble être le résultat des effets combinés de la recristallisation avec la croissance des grains qui l’accompagne et le glissement grain sur grain. Dans la gamme des températures allant de — 10^°C à — 40^°C, l’énergie apparente d’activation pour le fluage augmente comme la teneur volumique en inclusions. Ceci est apparemment dû à un processus d’activation thermique qui est modifié par les efforts internes produits par les inclusions.

Zusammenfassung

Der Einfluss der Korngrӧsse und verstreuter, fester Einschlüsse auf die Aktivationsenergie für das Kriechen von Eis. Stetige Kriechraten polykristallinen Eises wurden in Abhängigkeit von Temperatur, Korngrӧsse und Konzentration des Einschlüsse durch einachsige Kompression im Labor bestimmt. Die Proben wurden bei konstanter Last einem systematischen Wechsel der Temperatur zwischen etwa — 5^°C und — 40^°C unterworfen. Einschlüsse verhindern die dynamische Rekristallisation und das Kornwachstum; die mittlere Korngrӧsse bei Rekristallisation ist umgekehrt proportional zur Einschlusskonzentration. Bei Temperaturen über — 8^°C erhӧht sich die Kriechrate auf etwa das doppelte. Dies scheint das Ergebnis der kombinierten Wirkung von Rekristallisation mit Kornwachstum und Gleiten an den Korngrenzen zu sein. Im Temperaturbereich von — 10^°C bis — 40^°C wächst die scheinbare Aktivationsenergie für Kriechen mit wachsendem Volumen des Anteils an Einschlüssen. Dies beruht sichtlich auf einem thermisch verursachten Prozess, der durch innere Spannungen infolge der Einschlüsse abgewandelt wird.

Introduction

Within ice masses, crystal size, debris concentration, and temperature are all variables. However, the combined effect of these parameters on the flow of ice has never been investigated.

Recent studies have demonstrated that, at constant temperature and stress, the creep of polycrystalline ice with a random orientation of c-axes is quite sensitive to variations in ice-crystal size.Baker (1978) found that there is apparently an inversion between dislocation-controlled creep and diffusion-controlled creep at an average crystal size of about 1 mm and that this is an optimum grain-size for creep resistance. Increasing or decreasing the average crystal size from this critical value results in an increase in secondary creep-rate.

The first study of the influence of temperature on creep-rate was conducted by Glen (1955), who tested blocks of polycrystalline ice in uniaxial compression and showed that his data fit Arrhenius law with the secondary creep-rate obeying the following equation:

(1)

Here, A’ is a temperature-dependent constant, n≈3, σ is the applied stress, Q is the activation energy for creep, R is the gas constant, and T is the absolute temperature. Probably the most detailed study to date using inclusion-free ice, was conducted by Mellor and Testa (1969) who found a linear variation of log ϵ̇ with 1/T over a temperature range of —10 to —60°C. For this range of temperatures Q ≈ 67 kJ mol ⁻¹ (16 kcal mol⁻¹). At temperatures above —10°C, Glen (1955) and Mellor and Testa (1969) showed that the variation of log ϵ̇ with 1/T is non-linear and the Arrhenius relation (Equations (1)) for temperature dependence is invalid.

Prior to the present study, no detailed investigation of the effect of dispersed-solid inclusions on the creep of ice over a wide range of temperatures had been conducted. For a narrow range of temperatures near the melting point (above —10°C), Nayar (unpublished) found a non-linear variation of log ϵ̇ with 1/T for ice containing a 1% dispersion of fine silica particles.

Constant-temperature tests on inclusion-bearing ice have been conducted by Nayar and others (1971) and Hooke and others (1972). Both of these studies showed that creep-rate decreases exponentially with increasing volume fraction of dispersed particles. In addition, both studies showed scatter in the measured creep-rates at low inclusion concentrations. Variations in creep at low debris concentrations have also been reported by Butkovitch and Landauer (1958) and Swinzow (1962) who found, in the TUTO ice tunnel in Greenland, that tunnel closure rates were higher in slightly dirty ice than in clean ice.Baker (1978) showed that during freezing the presence of inclusions in low concentrations inhibits crystal growth so that an increase in the volume-fraction of inclusions results in a reduction in average ice-crystal size. Thus the variation in creep-rates observed in the earlier studies could be the result of grain-size differences among the samples due to variable inclusion concentrations.

Experimental procedure

Polycrystalline ice samples containing dispersed-solid inclusions were prepared by packing a porous mixture of well-sorted (having passed a 125 µm seive but retained on a 106 µm seive) Ottawa sand and powdered ice, made from deionized distilled water, into cylindrical moulds 19.5 mm in diameter and 100 mm long. The moulds were de-aerated and the void spaces filled by admitting air-free distilled water at 0°C. A 30 mm section was cut from the portion of the sample having the most uniform sand distribution, and the ends of this sample were carefully faced perpendicular to the long axis. Sample length and diameter, measured at twelve points, were determined using a micrometer which could be read to ±1 µm. After completion of the compression test, samples were halved and inclusion concentrations in the two halves determined by melting the ice and weighing the sand residue. By assuming a density of 0.9 Mg m⁻³ (0.9 g cm⁻³) for ice and 2.7 Mg m⁻³ (2.7 g cm⁻³) for sand, concentrations were reduced to volume per cent sand. Inclusion concentrations in the two halves of the same sample generally varied by less than 5% of the amount present.

A constant uniaxial load was applied parallel to the long axis of each sample. Tests were run in a cold laboratory, generally kept at about —10°C, using the ice-compression apparatus used by Baker (1978) in earlier deformation experiments. To prevent sublimation and control temperature, ice samples were immersed in a bath of kerosene. The bath was stirred with a miniature gear pump and temperature was controlled with a Lauda–Brinkman K-₄/R circulator. Bath temperature generally fluctuated less than 0.5 deg during a run.

Deformation measurements were made using a Hewlett Packard 7 DCDT-500 displacement transducer connected to a strip-chart recorder. Details of the deformation-measuring procedure were described by Baker (1978). Because stress differences between runs ranged from 0.53 to 0.57 MN m⁻² (5.3 to 5.7 bars), creep-rates were normalized to a stress of 0.56 MN m⁻² (5.6 bars) using the following relationship which is based on Glen’s flow law:

(2)

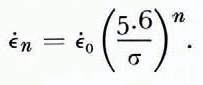
Here, ϵ̇ _n is the normalized secondary creep-rate, ϵ̇₀ is the experimental secondary creep-rate, and the other terms are as defined earlier.

To study the effect of temperature on creep-rate, samples were subjected to a constant load and secondary creep was established; then the temperature was systematically varied without relaxation of the applied load. This procedure was adopted instead of testing a number of samples at different temperatures over the same range of total strain because of the difficulties involved in making samples with identical macroscopic textures. A possible problem with this method is that it assumes that creep-rate is independent of dislocation distribution and density. However, since the density of dislocations during steady-state creep depends only on the applied stress (Bird and others, 1969), and since stress was held constant throughout each test, this procedure appears to be justified.

At each temperature setting, a minimum of 12 h was allowed for thermal equilibrium to become established before the strain-rate was measured. For most tests, the first and second temperature settings were — 5°C and — 40°C, respectively. The next four settings were alternated between these two extremes in a random order.

During the variable-temperature tests, which generally exceeded 400 h in duration, the sample diameter increased due to strain. This increase often resulted in a decrease in applied stress of as much as 0.02 MN m⁻² (0.2 bars). In an attempt to correct for this, the approximate sample diameter at the beginning of each temperature setting was calculated using the total strain versus time data and the fact that ice is incompressible. These values were then used to calculate the stress and strain-rate at each setting. As a check, the calculated final diameter was compared to the measured final diameter. In all cases the calculated value was slightly larger than the measured value—generally less than 1% larger. It is believed that this discrepancy is primarily due to sublimation during the tests.

Thin sections were cut from samples both before and after testing. These sections were photographed and average crystal size was determined from enlarged photographs using the maximum chord-intercept method of Krumbein (1935). This technique was recently shown to be highly efficient in approximating the true seive-diameter distribution from thin sections (Kellerhals and others, 1975). Since crystal sizes and shapes appeared to be uniform, it is assumed that this method provides an accurate measure of the average grain size. From a given thin-section photograph, the measured average crystal size was reproducible to within ±0.05 mm. The average crystal size from thin sections cut from both ends of samples generally varied by less than 0.1±0.05 mm; a grain-size difference of less than 10%. For a more detailed description of the experimental procedure, the reader is referred to Baker (unpublished).

Results

Results of the investigations into the effect of temperature on creep of both inclusion-free and inclusion-bearing ice are presented in Table I. Data from this table were used to make the diagrams of log ϵ̇ versus inverse temperature shown inFigure 1. From Figure 1., it can be seen that in some cases there is considerable scatter of points from a straight line through the data. This non-linearity is most pronounced, however, at temperatures above —10°C.

Table I. Effect of temperature on secondary creep-rate

Fig. 1. Effect of temperature on creep-rate of samples with varying volume fraction of inclusions. f is the volume fraction of inclusions present in the sample. Numbers next to data points show order in which tests on a given sample were made. On all points, error bars representing 99% confidence limits on the slope of the secondary creep curve (Krumbein and Graybill, 1965, p. 230) are smaller than dot. All creep data are plotted as uniaxial compressive strain-rates.

As mentioned previously, non-linear variation of log ϵ̇ with 1/T has been observed in other studies on polycrystalline ice (Glen, 1955; Nayar, unpublished; Mellor and Testa, 1969) Mellor and Testa (1969) argue that this variation is due to an increase in grain-boundary slip at higher temperatures. Weertman (1973), however, suggests that recrystallization and grain growth during creep tests could account for the non-linearity.

In the present study, recrystallization and grain growth were observed in all five of the samples tested (Fig. 2). From Table II and Figure 3, it can be seen that the amount of change in average crystal size due to recrystallization decreased with increasing volume-fraction inclusions.

Fig. 2. Thin sections of sample tested in uniaxial compression showing evidence for recrystallization and grain growth. Sample diameters are approximately 1.9 cm. (a) Thin section of sample before recrystallization. (b) Thin section of the same sample after recrystallization.

Table II. Summary of grain growth due to recrystallization

Fig. 3. The effect of dispersed inclusions on recrystallization of polycrystalline ice.

The role of inclusions in primary recrystallization of two-phase metal alloys has been treated in detail by Cahn (1965). He discussed how it is possible for a dispersed second phase to exert two opposed influences on a deformed alloy:

• (i) Nucleation of new grains may be accelerated if the second phase particles are large compared to the average crystal size. If they are small, nucleation is retarded or prevented altogether.

• (ii) Growth of grains is always impeded, because of the drag exerted on a migrating grain boundary by dispersed particles, especially if they are small and numerous.

In the present study, the inclusion size (0.1 mm) was approximately an order of magnitude smaller than the average ice-crystal size in all of the ice samples tested and Figure 3 suggests that the inclusions inhibited, rather than enhanced, crystal growth during recrystallization. According to Cahn (1965), the average crystal size produced by recrystallization is an inverse function of the concentration of dispersed inclusions. The trends observed for ice in Figure 3 are therefore compatible with recrystallization experiments from metals.

Baker (1978) conducted creep tests on inclusion-free ice at temperatures of about —9°C and detected virtually no grain growth. A. J. Gow (personal communication in 1974) has demonstrated that recrystallization of unstressed ice occurs rapidly, however, at temperatures approaching the melting point and when the recrystallization occurs under stress (dynamic recrystallization), this process is hastened considerably. Thus in the present variable-temperature tests, it seems reasonable to assume that most, if not all, recrystallization occurred during those temperature settings which were about —8°C or above.

The highest temperatures were generally employed at the last or next-to-last temperature setting. By measuring the amount of grain growth that occurred at this setting and knowing what effect this magnitude of grain-size variation should have on creep, it was possible to adjust these data to eliminate the effect of recrystallization (Fig. 4). The normalization procedure is as follows:

• (1) For each sample, the initial and final crystal sizes were used in conjunction with figure 2 of Baker (1978) to determine the approximate change (increase or decrease) in creep-rate due to recrystallization and grain growth.

• (2) This creep-rate increment, ∆ϵ̇, was then adjusted, using the normalization equation described by Baker (1978), in order to determine its value at the temperature settings in question (the settings above —8°C, where all grain growth is assumed to have occurred, and all subsequent settings).

• (3) These normalized creep-rate increments were then added to or subtracted from the measured creep-rate at each of the points in question.

Fig. 4. The effect of temperature on creep. f is the volume fraction of inclusions present in the sample, d is the average crystal diameter, and Q is the effective activation energy for creep in kJ mol⁻¹ (kcal mol⁻¹). Numbers next to data points show order in which tests on a given sample were made. Starred numbers are data points normalized to account for grain growth. (The unadjusted data are plotted in Figure 1.) Lines were fitted to the data gathered below —10°C using least-squares methods, with effective activation energies determined from the least-squares calculations. Error bars are smaller than the plotted dots

For example, the initial and final crystal sizes for sample A in Figure 1 were 1.22 mm and 2.14 mm, respectively. From figure 2 of the previous study (Baker, 1978) a change in grain size from 1.22 mm to 2.14 mm should result in an increase in creep rate ∆ϵ̇ of about 7.61×10⁻⁸ S⁻¹(2.4 year⁻¹) at —9.1°C. The temperature setting for data point 5 in sample A was —8.77°C. At this temperature the adjusted value of ∆ϵ̇ is (7.99×10⁻⁸ S⁻¹(2.52 year⁻¹). Thus, because of recrystallization, the creep-rate measured for point 5 is 7.99×10⁻⁸ S⁻¹ too high. Consequently, the adjusted value of ∆ϵ̇ (7.99×10⁻⁸ S⁻¹) is subtracted from the measured creep rate (1.28×10⁻⁷ S⁻¹) and the difference is plotted in Figure 4 as data point 5^⋆.

Discussion

Creep Enhancement Near the Melting Point

On the average, recrystallization and grain growth resulted in an 80% creep-rate enhancement near the melting point. By comparing Figure 4 with Figure 1, it can be seen that eliminating this effect makes the variation of log ϵ̇ with 1/T much more linear. Notice, however, that in all cases the highest temperature data (those above —8°C) are still displaced above a straight line drawn through the lower temperature points (Fig. 4). Thus, grain growth alone cannot totally account for the non-linearity of log ϵ̇ versus 1/T observed at temperatures above —8°C.

In a comprehensive discussion of high-temperature creep of ice, Barnes and others (1971) indicate that while grain-boundary sliding in ice may occur at lower temperatures, it is most important above —8°C where intergranular water occurs at the junctions of three or more crystals. They cite the works of Clifford (1967), Steinemann (1958), Nye and Frank (1973), Bell and others (1971), and Shreve (1972) for theoretical explanations as well as direct evidence of intergranular water in ice at temperatures down to —8°C. Mellor and Testa (1969, p. 141) also give evidence for intergranular water in their samples above temperatures of about —8°C based on electrical conductivity measurements. This is supported by the work of Jones and Brunet (1978) who found that for single crystals of ice above —8°C the variation of creep-rate with inverse temperature is linear. According to Barnes and others (1971), grain-boundary sliding normally relieves stresses developing within a sample, but it will also generate high stresses near triple junctions of grain boundaries. If liquid is present at the triple points, these high stresses are partly eliminated. Thus grain-boundary sliding and the liquid at triple points may play reinforcing roles in ice and result in creep-rate enhancement at temperatures above —8°C.

Following the ideas of Barnes and others (1971), if the non-linearity of log ϵ̇ versus 1/T at temperatures above —8°C in Figure 4 is due to the presence of liquid at triple junctions and grain-boundary sliding, then the average creep-rate enhancement due to these effects is approximately 25% (Fig. 4). This is certainly compatible with observations made on pure metals near their melting points where as much as 30% of the total strain may arise from grain-boundary shear (Hayden and others, 1965).

Thus, it appears that the non-linearity of log ϵ̇ with inverse temperatures near the melting point is due to the combined effects of crystal growth and grain-boundary sliding which play reinforcing roles affecting creep. The combination of these factors results in a creep-rate enhancement of about a factor of two.

Effect of Crystal Size and Inclusions on Diffusion at High Temperatures

It can be seen in Figure 4 that at a constant temperature of about —10°C, in general, creep-rate increases with increasing volume fraction of inclusions and, contrariwise, decreases with increasing inclusion concentration at temperatures of about — 40°C. Thus, in general, apparent activation energies for creep increase with increasing volume fraction of inclusions (decreasing average crystal size).

Raj and Ashby (1971) discuss how, at elevated temperatures, it is possible for grain-boundary sliding to be controlled by diffusional processes. They show how stresses developed along non-planar crystal boundaries can set up a diffusive flux of matter from portions of the boundary under compression to those under tension. If diffusion is the primary mechanism accommodating the incompatibilities caused by grain-boundary sliding, diffusional flow, and sliding are not independent. They are coupled and according to Raj and Ashby (1971, p. 1121) the resulting deformation is correctly described as “diffusional creep”, or as “grain-boundary sliding with diffusional accommodation”.

Recent investigations have shown that the creep-rate of fine-grained polycrystalline ice (d < 1 mm) is apparently controlled by diffusional processes (Baker, 1978). In the present study, all of the samples tested, with the exception of Sample A, had average crystal sizes of less than 1 mm. Thus, in order to discuss the increase in creep-rates with increasing volume fraction of inclusions at temperatures of about —10°C seen in Figure 4, it is necessary to derive an equation for diffusion-controlled creep which incorporates the influence of both grain size and solid inclusions.

The dual roles of bulk diffusion and grain-boundary diffusion in high-temperature creep have been discussed by Raj and Ashby (1971) and Gittus (1975) who modified the Nabarro-Herring creep equation to the following:

(3)

where δ is the width of a grain boundary, Ω is the atomic volume, k is Boltzmann’s constant, d is the average grain diameter, D_B and D_V are the coefficients for grain-boundary and bulk diffusion respectively, and the other terms are as defined earlier. From this equation it may be noted that at constant stress and temperature, if πδD _B /dD _V is much less than 1, the creep-rate is proportional to 1/d ². For ice at —10°C, D _V ≈ 1×10⁻⁹mm²s⁻¹ (Glen, 1974, p. 44), D _B ≈ 1×10⁻⁵ mm² s⁻¹ (Glen, 1974, p. 44), and δ = 9×10⁻⁸ cm (Goodman and others, (1977). Using d=1.22 mm (Sample A, Fig. 4) it follows that πδD _B/dD _V ≈ 0.023⪡ 1.Thus, from Equations (3), for inclusion-free ice (Sample A)

(4)

We will now proceed to derive an equation similar to Equations (3) but incorporating the influence of solid inclusions. If it can be assumed that grain-boundary sliding is the rate-determining process for high-temperature creep of fine-grained ice, the effect of inclusions on grain boundaries can be examined by using the analysis of Raj and Ashby (1971). This model gives creep-rate as a function of the rate of grain-boundary sliding u̇ where inclusions lie along the boundaries. That is,

(5)

where γ̇ is the shear strain-rate, τ is the shear stress, λ is the spacing between particles, a is the particle diameter and the other terms are the same as in Equations (3).

Although Equations (5) was derived from continuum considerations, Raj and Ashby discuss whether there should not be some microscopic influence of the particles which may provide a threshold stress below which no diffusional creep would take place. Vickers and Greenfield (1968) have considered the effect of inclusions along grain boundaries and discuss how inclusions oppose diffusional creep because they exert internal stresses σ_i which oppose the applied stress. Thus the stresses causing flow are lower, and the applied stress should be reduced to an effective stress

(6)

Taking this into account and using the Lévy–Mises equivalent (ϵ̇/σ = γ̇/3τ) for comparison with compressional strain-rates, Equations (5) becomes

(7)

In order to use this equation for analysis of the data presented in Figure 4, it is necessary to express the particle spacing λ in terms of particle size a and volume fraction of inclusions f. Baker (1978) has derived such an expression, finding that particle spacing depends upon inclusion size and concentration according to the relationship

(8)

From Equations (7) and (8), assuming all inclusions are on crystal boundaries (a reasonable assumption since Baker (1978) found 87% of the included sand particles in similar samples were located on grain boundaries), it is found that

(9)

It can be seen from this equation that at constant temperature, stress, and volume fraction of inclusions, creep-rate is again proportional to the inverse square of the grain-size.

The diameter of inclusions used in the present study was 0.1 mm. Thus, at a temperature of —10°C, the term 5δD _B/aD _v ≈ 0.45. Using this value as well as the grain-size and volume-fraction inclusion data from Figure 4, relative creep-rates can be calculated using Equations (9) and compared to the result obtained from Equations (3) for inclusion-free ice. These results are given in Table III.

Table III. Effects of average crystal size and volume-fraction inclusions on relative creep-rate

If the results in Table III are now compared with the data at —10°C in Figure 4, several important trends can be observed. First, in Figure 4 it is found that creep-rates increase with increasing volume fraction of inclusions; a result predicted in Table III although the high creep-rates predicted at 0.013 and 0.022 volume-fraction inclusions were not found experimentally. Secondly, at volume-fraction inclusions higher than 0.04, the predictions in Table III show the creep-rate to be approximately constant. This agrees well with the measured creep-rates at —10°C presented in Figure 4 (Samples D and E). Normally, variations in inclusion concentration and average crystal size have competing effects on creep-rate, which decreases with increasing volume-fraction inclusions and increases with decreasing grain size (Equations (9)). Thus, the constant creep-rate at higher volume-fraction inclusions may indicate that the competing effects of increasing inclusion concentration and decreasing crystal size are cancelling one another (d ²f ≈ constant).

Equations (3) and (9) predict similar trends to those indicated in Table III throughout the entire range of temperatures in Figure 4. However, if the data at about — 40°C (Fig. 4) are examined, it can be seen that, in general, creep-rates decrease with increasing volume-fraction inclusions. This trend is inconsistent with that predicted in Table III if one considers the inclusion-free versus the inclusion-bearing samples. Furthermore, Equations (3) and (9) predict an opposite trend in apparent activation energies than that observed in Figure 4. Thus, a simple model for grain-boundary diffusion over the full range of temperatures is by itself insufficient to explain the results in Figure 4.

Effect of Inclusions on Activation Energy

Since the previous model does not fit the experimental data over the full range of temperatures, it appears that another rate-limiting step or steps may be controlling creep at low temperatures. Thus, a simple thermal-activation approach to creep will be adopted in order to test the effect of rigid inclusions on activation energy.

Kocks and others (1975) show that by beginning with a creep equation such as that of Dieter ([^C1976], p. 470)

(10)

where A is a constant, Q is the true activation energy for creep, v is the activation volume, and the other terms are as defined previously, the effect of internal stresses due to inclusions can be incorporated so that Equations (10) becomes

(11)

From this equation, it can be seen that the internal stress σ_i combines with the true activation energy Q indicating that the apparent activation energy Q₀ is a measure of both thermal activation and internal stress (Q₀=Q+νσ_i). Thus, inclusion-bearing samples should have higher apparent activation energies than inclusion-free samples and since σ_i increases with increasing volume-fraction inclusions, so should apparent activation energies. As an example, Vickers and Greenfield (1968) found for pure magnesium at about 0.8T _m, the true activation energy was 134 kJ mol⁻¹ (32 kcal mol⁻¹) while for magnesium containing a 1% dispersion of fine magnesium oxide, the apparent activation energy was 419 kJ mol⁻¹ (100 kcal mol⁻¹). Thus the increase in apparent activation energy with increasing volume fraction of inclusions observed in Figure 4 appears to be the result of a thermally activated process which is modified by the internal stresses created by the included sand particles.

Alternatively, the thermal-activation equation of Kocks and others (1975, p. 108) could be adopted.

(12)

Here However, over the range of temperatures employed, this yields essentially the same result as Equations (11).

The magnitude of the internal stress term was estimated in two unique ways. First, one may associate the ν value in Equations (11) with the shear activation volume V^⋆ of the deformation process. If the activation volume were relatively constant, then a plot of apparent activation energy versus volume fraction of inclusions would give the strength of the internal stress term. Estimating V^⋆ as b ²l, with the burgers vector b equal to 4.52 Å and l ≈ λ from Equations (8), one determines V ^⋆ to range from about 4.0 to 6.1×10^–19 cm³. If these values are now used to estimate the strength of the internal stress term, very realistic estimates of 0.036 to 0.141 MN m⁻² (0.36 to 1.41 bars) result; values which are approximately 6 to 25% of the applied creep stress. Furthermore, the internal stresses increase with increasing volume fraction of inclusions as might be expected. A second method of estimating the internal stresses would be to assume they are Orowan stresses (Orowan, 1948) using λ and b as above with an elastic modulus of 9.5×10³ MN m⁻² (Hobbs, 1974). This gives values of 0.028 to 0.044 MN m⁻² (0.28 to 0.44 bars) which increase with inclusion concentration. In either case, these are significant internal stresses which could account for the apparent increase in activation energy measured experimentally.

The only previous study which made measurements of the effect of temperature on creep of inclusion-bearing ice (Nayar and others, 1971), did so in the temperature range of —2°C to —13°C—temperatures where grain-boundary sliding can be enhanced by the presence of intergranular water. Their results showed that the apparent activation energy for creep of ice containing a 1.0% dispersion of ultra-fine amorphous silica (average particle diameter 1.5×10⁻⁵ mm) was 406 kJ mol⁻¹ (97 kcal mol⁻¹) ; approximately three times the activation energy for creep of clean ice measured over the same temperature range (Glen, 1955; Mellor and Testa, 1969; Barnes and others, 1971). This is in qualitative agreement with the apparent activation energies measured over a lower range of temperatures in the present study.

Because average crystal size decreased with increasing volume-fraction inclusions, the possibility remains that the activation energy for creep is influenced by variations in ice-crystal size. In the present study, no tests were conducted on the variation of log ϵ̇ with 1/T for inclusion-free ice with different grain-sizes. However, a number of previous studies of the effect of temperature on creep of polycrystalline ice have made at least approximate measurements of average crystal size. These are summarized in Table IV. Although in most cases the grain-size measurements were not precise, no systematic relationship between activation energy and crystal size is apparent. On this basis, it appears that variations in ice-crystal Size have little or no effect on activation energy for creep and that the differences in Q observed in Table IV may have been due to other factors such as creep-rate enhancement at high-temperature settings due to the presence of intergranular water; possible recrystallization and grain growth at the high-temperature settings; and possible variations in the orientation of c-axes among the samples tested. This matter, however, clearly warrants further detailed study.

Table IV. Values of activation energy for creep and grain-size from steady-state creep tests on polycrystalline ice