Introduction
In order to understand the flow of glaciers and ice sheets it is necessary to know at what rate ice deforms under various stresses. Many calculations have been made assuming ice to be a Newtonian viscous fluid (see, for example, SomiglianaReference Somigliana 1 ), but NyeReference Nye 2 has suggested an alternative model, taking ice to be an ideally plastic solid. To determine the actual behaviour of ice, laboratory tests should be performed so that, as far as possible, the stress is the same throughout the specimen and the temperature conditions are known and comparable from test to test. The grain size of the specimen and the preferred crystal orientation, if it exists, should also be known.
Most tests performed in the past have, unfortunately, failed to meet these requirements ; thus the experiments of McConnell and KiddReference McConnell and Kidd 3 and of HessReference Hess 4 were carried out in the open air, and hence temperatures varied widely between tests and even during a single test. Other investigators such as Weinberg,Reference Weinberg 5a , Reference Weinberg b Kobeko and co-workersReference Kobeko, Shishkin, Marey and Ivanovo 6 and LavrovReference Lavrov 7 have used torsion or bending tests, in which the stress varies from place to place within the specimen, and have calculated a coefficient of viscosity from their data. The discrepancies between the various values obtained together with measurements taken by HöpplerReference Höppler 8 using a viscometer, are sufficient to suggest that the viscosity of ice varies markedly with the applied stress and thus cannot be considered as constant, even at a given temperature. Wartime experiments undertaken in connection with the iceberg-ship project convinced PerutzReference Perutz 9 that ice showed creep properties similar to those of metals, and provided the stimulus for this investigation.
The present experiments are designed to test specimens of ice in tension or compression under controlled temperature conditions. With this object in view methods have been devised for growing single crystals of ice of length about 3 cm. and diameter about 0.4, cm. for use in tension tests, and for preparing polycrystalline compression specimens in which the individual crystal grains are equiaxed and as randomly oriented as possible. For convenience in testing, these specimens were prepared in two sizes, namely 2 in. (5.1 cm.) long with diameter 1 in. (2.5 cm.) and 4 in. (10.2 cm.) long with diameter 2 in. (5.1 cm.). This paper gives details of the method of preparation of these specimens and some preliminary results of compression tests on the polycrystalline cylinders.
Experiments
Ice formed on the surface of a bowl of water which is allowed to freeze consists of columnar crystals with the optic axis as their long axis perpendicular to the surface. If a piece of glass tubing is held under freezing water and at an angle to the surface, one or two of the columnar crystals enter the top of the tube and then grow along it. The ice formed in the tube is therefore often found to be a single crystal with its optic axis vertical, and thus it is possible to obtain a single crystal in the form of a cylinder and with its optic axis at any desired angle to the cylinder axis. Ice is believed to deform by slip of thin layers perpendicular to the optic axis ; when a single crystal is pulled, the shear stress tending to produce this slip is greatest when the optic axis is at 45 degrees to the cylinder axis. The diagram in Fig. 1 (p. 113) shows the type of deformation which is envisaged, and the photograph shows a specimen of such an orientation which has been stretched to nearly twice its original length ; the right half, which has been turned through a right angle relative to the left half, shows that the ice crystal has become a thin tape, and optical measurements confirm that the optic axis has become more nearly perpendicular to the tension axis.

Fig. 1. Single crystal of ice, initially 25.4 mm. between grips, 13 mm.2 cross-section, optic axis at 45° to cylinder axis. Pulled with load of 400 gms. The diagram below shows schematically the initial and final states of the crystal supposing slip to have taken place on the basal plane
The polycrystalline specimens are obtained by filling a cylindrical mould with rime collected from the pipes of a refrigerator, evacuating the mould, sucking in ice-cold, air-free distilled water and allowing this to freeze, using the rime particles as nuclei. The resulting specimens are not totally bubble free but their density is the same as that recorded for natural ice, their mean grain diameter being about 1 to 2 mm.
Some of these polycrystalline specimens have been tested in a small testing machine placed inside a large refrigerator, readings being taken through a double window in the door of the refrigerator. The machine compressed the ice cylinders by means of weights hung directly below the specimen ; this gave stresses varying from 0.9 to to bars (1 bar is 106 dyne cm.−2≃1 Kg. cm.−2). The deformation of the specimen was measured with a sensitive dial gauge. Throughout all the tests the temperature varied from −0.8° C. to −2.5° C. with a mean temperature of −1.5° C. Owing to the time taken by some of these tests, especially at the lower stresses, the specimens evaporate seriously and, to overcome this, some tests were performed with the specimen immersed in paraffin. The results of these tests agreed with those of tests performed in air provided allowance was made for evaporation in calculating the stress in the latter case.
Results
When a load is suddenly applied to ice, it deforms almost instantaneously to a certain strain and then deforms more slowly as the time proceeds. This slow deformation is known as creep and has been observed for many solid substances; AndradeReference Andrade 10a , Reference Andrade b showed that in many cases it consists of a transient part and a continuing part, and it is this continuing part which is of interest in the theory of glacier flow, as it enables ice to flow continuously under the action of a stress.
A typical time-deformation curve for one of the compression specimens is shown in Fig. 2 (p. 112). After bo hours this curve becomes effectively a straight line, the slope of which, divided by the specimen length, gives the strain rate. Fig. 3 (p. 112) shows the result of plotting these strain rates against the stresses required to produce them. For a Newtonian viscous liquid these points would lie on a straight line through the origin, and the extent to which the observed points deviate from this shows how bad an approximation a constant coefficient of viscosity is in the case of ice. Plotting the logarithm of strain rate against the logarithm of stress (Fig. 4, p. 112) gives a relation which, in the stress range from 1.5 to 10 bars, is approximately linear, that is to say the relation between compressive stress σ and compressive strain rate ![]() is of the form
is of the form
where k and n are constants.

Fig. 2 A typical creep curve. Specimen No. VIII, length 10.2 cm., diameter 4.63 cm., load 48 kg. After 60 hours the curve is effectively a straight line

Fig. 3 The variation of the steady state creep rate with stress. Two points had to be omitted at 9.4 bars a strain rate of 128.4 years−1 and at 10.5 bars a strain rate of 87 years−1. The line is the straight line from Fig. 4

Fig. 4. Double logarithmic plot of the data in Fig. 3. The straight line corresponds to the relation
The straight line drawn in Fig. 4 corresponds to a relation of this form in which n=4 and, if σ is measured in bars and ![]() in years−1, k is equal numerically to 0.074.
in years−1, k is equal numerically to 0.074.
The effect of temperature on these results remains to be investigated, in particular very close to the melting point, and it is hoped that the amount of deformation occurring in the grain boundaries by mutual movement of the grains may be estimated from the results of tests on the single crystal specimens. Fuller results of this work will be published later.
I wish to thank Dr. E. Orowan and Dr. M. F. Perutz for many helpful discussions, and also the Department of Scientific and Industrial Research for a maintenance grant.

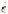 . For the stress range 1.5–10 Kg. cm
. For the stress range 1.5–10 Kg. cm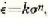 , where n is a constant equal to about 4. A method of preparing small cylindrical single crystals of ice of a desired orientation is also described.
, where n is a constant equal to about 4. A method of preparing small cylindrical single crystals of ice of a desired orientation is also described.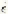 ziemlich kompliziert ist. Für den Druckbereich 1.5–10 Kg. cm.
ziemlich kompliziert ist. Für den Druckbereich 1.5–10 Kg. cm.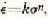 wobei
wobei 



