Introduction
Groundwater flow in a pressurized subglacial system influences ice-sheet stability and movement mechanisms as well as the nature of the sediments and landforms left after the glacier retreats (Reference PiotrowskiPiotrowski, 2006). Previous work modeling ice-sheet–groundwater interactions has contributed to our overall understanding of subglacial groundwater systems. Some earlier numerical simulations indicate that groundwater velocity was altered and that flow directions in northern Europe were even reversed under the influence of past ice sheets. Reference Boulton and DobbieBoulton and Dobbie (1993) argued that during the Saalian glaciation, aquifers in Holland would have been able to transmit all the basal meltwater. Their study showed that where glaciers rest on high-transmissivity sediments, no additional drainage system is needed for the evacuation of meltwater. Similarly, in a large-scale study of western Europe and Scandinavia, Boulton and others (1995) suggested that marginal areas beneath the Scandinavian ice sheet would have had high enough transmissivities to discharge all the meltwater via groundwater flow alone. However, in areas where the rocks of the Precambrian Fennoscandian Shield were not able to transmit all the meltwater, excess water would have been discharged via sheet flow or conduits at the ice/bed interface. Furthermore, Reference PiotrowskiPiotrowski (1997) suggested that aquifers with low transmissivity in northwestern Germany could only have evacuated about 25% of the subglacially produced meltwater from the system during the last glaciation.
Reference Arnold and SharpArnold and Sharp (2002) constructed a two-dimensional time-dependent ice-sheet model that included the basal hydrology, assuming a hard bed. Their model indicated that the behavior of the Scandinavian ice sheet depended greatly on the influence of the ice-sheet surface topography because the subglacial head gradient is partially controlled by the ice-surface profile. Reference Breemer, Clark and HaggertyBreemer and others (2002) modeled groundwater flow beneath the Lake Michigan Lobe of the Laurentide ice sheet during the last glaciation. They argued that subglacial aquifers were incapable of transmitting all the basal meltwater, and that a 7–8mm water film, or equivalent channel network, at the ice/bed interface would have been necessary to remove enough meltwater to maintain pore pressure at values less than the overburden pressure of the overlying ice.
To investigate a groundwater-flow system on the western margin of the Scandinavian ice sheet, we also used a groundwater-flow model. Our groundwater model includes the flow of basal meltwater through the subglacial aquifer, using methods similar to those used by Reference Breemer, Clark and HaggertyBreemer and others (2002). However, our model is linked to a two-dimensional, time-dependent, thermomechanically coupled finite- element ice-flow model along the same flowline. The aims of this study are to utilize the groundwater model to (1) test the flow capacity of the aquifer along this flowline to transmit meltwater, (2) study the importance of an integrated subglacial drainage system at this location and (3) assess the effects of different ice-margin positions on subglacial hydrology.
The ice-flow model, which is linked to our groundwater model, has been applied in several studies of the Laurentide ice sheet (Reference Cutler, MacAyeal, Mickelson, Parizek and ColganCutler and others, 2000, Reference Cutler, Mickelson, Colgan, MacAyeal and Parizek2001; Reference Winguth, Mickelson, Colgan and LaabsWinguth and others, 2004) and also on the Scandinavian ice sheet (Reference Winguth, Mickelson, Larsen, Darter, Moellerand and StalsbergWinguth and others, 2005). The ice-flow model calculates ice thickness and extent, as well as basal melting, mainly using climate data and topography as input (Reference Cutler, MacAyeal, Mickelson, Parizek and ColganCutler and others, 2000, Reference Cutler, Mickelson, Colgan, MacAyeal and Parizek2001; Reference Winguth, Mickelson, Colgan and LaabsWinguth and others, 2004, Reference Winguth, Mickelson, Larsen, Darter, Moellerand and Stalsberg2005). Basal meltwater production values derived from the ice-flow model are used as recharge input to the groundwater model, and the ice-sheet topography resulting from the ice-flow model is used to compare resulting pore-water pressures with the ice overburden pressures. The basal hydrology is modeled under two conditions: (1) allowing transmission of water only through the sediments and (2) allowing an additional drainage path for excess meltwater. Both of these conditions are then modeled for different ice-margin positions during the Weichselian.
The modeled flowline lies within Nordfjord, an east– west-trending fjord in the western fjords region of Norway, located at approximately 62° N (Fig. 1). This region is modeled so that basal meltwater rates from the ice-flow model of Reference Winguth, Mickelson, Larsen, Darter, Moellerand and StalsbergWinguth and others (2005) can be used. The basement rock along the flowline is dominantly banded, granitic gneiss.

Fig. 1. Study area in southwestern Norway, showing the ice extents at the Last Glacial Maximum (LGM) and the Younger Dryas. The white dashed line marks the flowline, which starts at the present-day glacier of Jostedalsbreen, runs through Nordfjord and ends offshore at 603m water depth.
Since the Eemian interglacial, four major advances of the ice sheet have reached the continental-shelf edge (Reference Sejrup, Larsen, Landvik, King, Haflidason and NesjeSejrup and others, 2000). The last of these was between 28 and 22 kyr BP. The ice margin retreated to a position near the present coastline around 20 kyr BP (Reference Rye, Nesje, Lien and AndaRye and others, 1987; Reference Valen, Mangerud, Larsen and HufthammerValen and others, 1996) and was followed by the less extensive Tampen readvance between 18 and 15 kyr BP (Reference SejrupSejrup and others, 1994, Reference Sejrup, Larsen, Landvik, King, Haflidason and Nesje2000; Reference Nygård, Sejrup, Haflidason, Cecchi and OttesenNygård and others, 2004). The majority of the till from the Late Weichselian glaciations was deposited in marginal zones on the shelf and within the shelf’s tributaries in the main valleys of Nordfjord below the marine limit. Around 13 kyr BP, the time of the Davik stadial, the ice margin was once again near the coastline, and then retreated to the head of the fjord by 12 kyr BP(Reference FarethFareth, 1987). Subsequent pulses of glaciation occurred throughout the Holocene, and several moraines of these ages are found in Erdalen, the valley that lies at the proximal end of our flowline.
Methods
Numerical code and model design
Groundwater flow beneath the Scandinavian ice sheet is simulated using the finite-difference code, MODFLOW (Reference McDonald and HarbaughMcDonald and Harbaugh, 1988). The code can simulate three-dimensional, transient flow of groundwater of constant density through porous material using a partial differential equation derived using Darcy’s law and a mass-balance equation:

where Kx , Ky and Kz are values of hydraulic conductivity (m s–1) in the x, y and z coordinate directions, h is head (m), W is a volume flux per unit volume where negative values are extractions and positive values are injections, or recharge (s–1), Ss is the specific storage of the porous medium (m–1) and t is time (s). We modeled two-dimensional, steady-state flow in a homogeneous, anisotropic aquifer, so Equation (1) reduces to
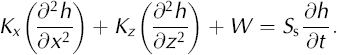
A complete derivation of the groundwater-flow equation can be found in Reference McDonald and HarbaughMcDonald and Harbaugh (1988).
The preprocessor, Groundwater Vistas, developed by Reference Rumbaugh and RumbaughRumbaugh and Rumbaugh (2001), was used as a graphical user interface with the MODFLOW code. The hydrostratigraphy along the flowline was defined by specifying values of hydraulic conductivity for the sediment cover in the fjord. The Norwegian Geological Survey is conducting detailed field investigations into the distribution of sediment throughout this fjord, but currently the Pre-Weichselian sediment thickness and distribution are not known, so present-day sediment thickness was used. Much of the sediment may have been eroded as the ice advanced (Reference Hooke and ElverhøiHooke and Elverhøi, 1996), but we assume a near-maximum sediment thickness to test whether even a thick sediment layer could have removed the water. For the offshore region, sediment thickness estimates from a study about 150 km farther south are used (Reference Sejrup, Aarseth and HaflidasonSejrup and others, 1991). The sediment thickness values present in the groundwater-flow model precisely match those used in the ice-flow model of Reference Winguth, Mickelson, Larsen, Darter, Moellerand and StalsbergWinguth and others (2005).
We assume the time that the ice front remained stationary was greater than the time necessary for the groundwater system to equilibrate such that steady-state conditions prevailed. We also assume that groundwater flow was parallel to the ice flowline, because subglacial head gradients are directed by driving pressure defined by the ice-surface profile (Reference PatersonPaterson, 1994, p. 112–124). Additionally, the rock walls of the fjord would have prevented significant lateral movement of groundwater.
The two-dimensional, thermomechanically coupled ice- flow model (Reference Winguth, Mickelson, Larsen, Darter, Moellerand and StalsbergWinguth and others, 2005) calculates ice flow along the same flowline as the groundwater model and computes basal meltwater production that is input as recharge to the groundwater model. The ice-flow model runs transient simulations for the full glacial cycle, providing groundwater recharge rates of meltwater for several positions of the ice margin. Where the bed is below the pressuremelting point, no meltwater is added to the groundwater system. Groundwater models are constructed for six ice- margin positions derived from the ice-flow model: 32, 30.5, 29.7, 27.5, 21 and 14.5 kyr BP (Reference Winguth, Mickelson, Larsen, Darter, Moellerand and StalsbergWinguth and others, 2005). Margin positions at 32 and 30.5 kyr BP represent the first stages of ice advance. The margin position at 29.7 kyr BP corresponds to the maximum ice extent. The model for 27.5 kyr BP characterizes a minor retreat phase. The Tampen readvance is modeled with the 21 kyr BP margin position and deglaciation is modeled with the 14.5 kyr BP margin position.
Using the ice-flow model allows us to input calculated estimates of recharge (meltwater) to the groundwater flow. In addition to the basal meltwater production values, the calculated ice thickness from the ice-flow model is also crucial in interpreting the results of the groundwater model because pore-water pressures calculated from the potentio- metric surfaces simulated by the groundwater model are compared to the ice overburden pressures calculated from the ice-surface topography. In a natural setting, the evolving ice-surface topography has an important influence on subglacial water flow because it controls the resulting variations in the subglacial hydraulic potential driving the groundwater flow.
Boundary conditions and input parameters
The eastern end of the flowline is east of Erdalen, close to the present-day ice divide of Jostedalsbreen. This up-gradient end of the flowline is represented by a no-flow boundary, which corresponds to the ice-flow divide (Fig. 2). The fjord is underlain by relatively impermeable crystalline bedrock, which is represented as a no-flow boundary at the base of the model. The down-gradient end of the flowline is a specified head boundary, which represents sea level for each corresponding ice-margin position. Since the flowline is approximately 311 km long at its greatest extent, a relatively coarse grid is used where each cell is 1000 m in length, with varying cell heights according to the surface topography and sediment thickness. The flowline extends beyond each ice- margin position to include a discharge zone that encompasses an area about 1 km beyond the ice margin. The number of active cells in each simulation depends on the ice-margin position.

Fig. 2. A conceptual diagram of the groundwater model construction and boundary conditions. The flowline is 3 x 105 m in length, with a maximum elevation of 1200 m. Topography and sediment thickness are not to scale.
Basal melting is included in the groundwater model by inputting the basal meltwater as recharge, set according to the melting rates calculated by the ice-flow model. The calculated recharge rates range from 9 x 10–4 to 2 x 10–2 m a–1. The first sets of simulations were run with a two-layer model where the bottommost layer represents crystalline bedrock, and has a conductivity near zero. The banded granitic gneiss of this region has no primary porosity, but secondary porosity may allow some water to flow into it (Reference Clark, Douglas, Raven and BottomleyClark and others, 2000), especially in zones of higher pressure beneath the ice. By assigning a small hydraulic conductivity to the crystalline bedrock, we allow for slight downward movement of water into the bedrock, though in most simulations the amount of such vertical flow is negligible.
The sediment thickness in the groundwater-flow model matches that of the ice-flow model of Reference Winguth, Mickelson, Larsen, Darter, Moellerand and StalsbergWinguth and others (2005). The upper model layer represents the sediment layer draping the bedrock ranging from 1 to 281 m thick. Since information regarding stratification and lateral heterogeneities is limited, the sediments are represented as one homogeneous layer (Table 1). A sediment layer occurs directly under most glaciers and is of particular significance because it is the first unit encountered as meltwater infiltrates into the subsurface (Reference PiotrowskiPiotrowski, 2006). Hydrogeological parameters are difficult to estimate, as the hydraulic conductivity of subglacial till from past glaciations ranges as much as 10–1 to 10–12 m s–1 (Reference Freeze and CherryFreeze and Cherry, 1979). In our model, we used a hydraulic conductivity of the subglacial till and sediment layer of 10–4ms–1 (Reference Stephenson, Fleming, Mickelson, Back, Rosensheim and SeaberStephenson and others, 1988). Similar values for hydraulic conductivity are reported in in situ studies of modern glaciers (e.g. Reference FountainFountain, 1994; Reference Iverson, Jansson and HookeIverson and others, 1994; Reference Iken, Fabri and FunkIken and others, 1996). To account for anisotropy in the sediment and bedrock layers, the vertical hydraulic conductivity (Kz) is one order of magnitude less than horizontal hydraulic conductivity (Kx).
Table 1. Hydraulic conductivity, Kx , used in the groundwater model. K z is one order of magnitude less, except for the drainage layer which is assumed to be isotropic

In additional model runs for each ice-margin position, a third layer was added to the two-layer model, placed on top of the sediment layer to provide additional drainage for basal meltwater. There is broad agreement among glaciologists that water at the ice/bed interface flows in one of two conceptually different flow systems, commonly termed ‘channelized’ and ‘distributed’ (Reference Fountain and WalderFountain and Walder, 1998). In both channelized and distributed drainage systems most of the basal meltwater may evacuate through conduits, allowing very little infiltration into the aquifer (Reference Fountain and WalderFountain and Walder, 1998). The drainage layer in our model is assigned a relatively high hydraulic conductivity (Table 1) and is used to represent drainage through what was probably a complex system of drainage channels or a continuous water film. The drainage layer was represented as a 1 m thick layer in the model, and the hydraulic conductivity assigned to the drainage layer in each model was specified so that the pore pressure in the underlying sediment layer was slightly less than the overburden pressure of the ice. In this way the minimum volume of meltwater was allowed to drain so that pore-water pressure was kept below ice overburden pressure in order to prevent flotation of the ice (Reference PatersonPaterson, 1994, p. 146–151). If the drainage system beneath the ice was more efficient (i.e. if we had assumed a higher effective hydraulic conductivity), greater volumes of water would have drained through the drainage layer, and the pore pressure in the sediment layer would have been lower.
The three-layer model is used to determine how much water can be transmitted through the sediments under conditions in which the ice is stable, i.e. pore-water pressure is below flotation level. Pore-water pressure is calculated from the simulated heads. First, the normal stress is approximated as (Reference PatersonPaterson, 1994, p.410–412)
where pi is the density of ice (900 kg m–3), g is gravitational acceleration (9.81 ms–2) and bi is ice thickness (m). The pore-water pressure, Pw, is equal to
where h is head (the elevation above an arbitrary datum to which water will rise in a piezometer inserted into the bed), z is the elevation of the measuring point above the datum and p is the density of water (1000 kN m–3).
By specifying that the pore-water pressure must be less than the ice overburden pressure and that the profiles of the potentiometric surfaces are less than approximately 90% of the ice thickness, the model provides an estimate of the maximum percentage of basal meltwater that the sediments can transmit out of the fjord.
Limitations of modeling
The results of the groundwater model in this study show that the sediment layer used has a limited ability to transmit basal meltwater, and that other drainage systems must have existed in fjords along the western edge of the Scandinavian ice sheet unless the sediment layer was much thicker or much more permeable. The groundwater model, however, does not consider feedback between the aquifer and the stability of the ice sheet. In addition, the simulations are run in steady state and do not account for advancing ice and possible compression of the aquifer. In order to fully model the connection between basal conditions and ice flow in the area, a completely three-dimensional coupled model is needed. Ice-flow models for this project (Reference Winguth, Mickelson, Larsen, Darter, Moellerand and StalsbergWinguth and others, 2005) are thermomechanically coupled, but simulate ice flow in two dimensions. To simulate three-dimensional groundwater flow, where local heterogeneities may aid or hinder the transmission of basal meltwater, it would be necessary to extrapolate the two-dimensional ice-sheet modeling results to three dimensions for input to a threedimensional groundwater model.
Modeling Results
Two-layer model
The objective of the groundwater modeling was to determine the transmission capacity of a reasonable maximum thickness of sediment underlying the ice in Nordfjord during the time of the Late Weichselian glaciation. The first sets of simulations were run using the two-layer model. The results of the groundwater model are examined in two ways: by comparing pore-water pressures to ice overburden pressure, and by plotting the potentiometric surface and the ice- surface profile. In a glacial environment, the groundwater flow confined by an ice sheet is driven by a hydraulic gradient determined by the ice-surface slope. The resulting potentiometric surface should run approximately parallel to the ice surface at a depth corresponding to the water pressure (Reference Fountain and WalderFountain and Walder, 1998).
For all the ice-margin positions examined, except the simulation for significant glacial retreat (14.5kyr BP), pore- water pressures far exceed the ice overburden pressures using the two-layer model settings. The resulting potentio- metric surfaces generated by the groundwater models are well above the ice surface for all the examined ice-margin positions (Fig. 3). The unrealistically high heads calculated in these simulations drive all the basal meltwater through the thin layer of sediments, and under these hydraulic conditions flotation of the ice sheet will occur. Assigning a higher hydraulic conductivity to the sediment layer will cause the heads to be lower, but it is unlikely that the hydraulic conductivity of these sediments was much greater than 10–4ms–1 (Reference Stephenson, Fleming, Mickelson, Back, Rosensheim and SeaberStephenson and others, 1988; Reference PiotrowskiPiotrowski, 2006). Hence, it is likely that, under these simulated meltwater conditions, the sediments would have been incapable of transmitting all the basal meltwater out of the fjord.

Fig. 3. Profiles of the potentiometric surface from the two-layer model for each simulated ice position.
The change in basal water pressure over time is examined by looking at the groundwater models for each ice-margin position. Surface topography, ice thickness and the total volume of basal meltwater entering the groundwater-flow simulation greatly impact the basal water pressure. Since the amount of basal meltwater entering the groundwater system is largely controlled by the extent of the ice and the length of the modeled flowline, the model for the Late Weichselian maximum position (29.7 kyr BP) has the highest pore-water pressures. Pore-water pressures resulting from the two-layer model are lowest during retreat phases, and rise only slightly during the Tampen readvance (Fig. 3).
The two-layer model does not allow for the flow of water at the ice/bed interface, so all the basal meltwater must be transmitted through the underlying sediments. The ice overburden pressures calculated from the ice-surface topography of the two-dimensional ice-flow model range from 12 to almost 20 MPa (Reference Winguth, Mickelson, Larsen, Darter, Moellerand and StalsbergWinguth and others, 2005). Pore-water pressures from the two-layer groundwater model simulations for all the ice margin positions, except 14.5 kyr BP, far exceed those values. This suggests that for these ice margin positions, some other source of drainage must have been available in order to keep pore-water pressures below overburden pressure and to avoid flotation of the ice sheet.
The groundwater model for the 14.5 kyr BP ice-margin position, which represents a major glacial retreat, shows that the sediment layer is actually capable of transmitting all the basal meltwater. In initial runs, we assumed that the groundwater model is not recharged by significant surface meltwater. However, as a glacier retreats, there is typically an increase in the routing of surface melt to the bed, either through the formation of moulins and englacial conduits, or due to changes in the porosity of the ice (Reference Fountain and WalderFountain and Walder, 1998). In areas where these englacial conduits extend to the bed, the amount of surface melt contributed to the ice/bed interface could be greater than the basal meltwater contribution by several orders of magnitude. If the total amount of recharge in the 14.5 kyr BP simulation is increased by one order of magnitude, results are qualitatively similar to those of the other ice-margin positions, and pore-water pressures are much higher than the ice overburden pressure. Thus, with this minimal increase in recharge, other modes of water evacuation from the subglacial system are necessary to produce reasonable pore pressures.
Three-layer model
In order to obtain better estimates of the transmission capacity of the sediments underlying the ice, and to attempt a more accurate modeling of the subglacial conditions, the three-layer model, with a drainage layer over the sediments, was tested for each of the ice-margin positions. In model runs, more of the basal meltwater is diverted to the drainage layer as its hydraulic conductivity is increased, and the volume of basal meltwater transmitted through the sediment layer decreases. The volume of water transmitted through the sediment layer when the pore-water pressure is just below the ice overburden pressure must represent the maximum volume of meltwater that this layer can transmit.
The three-layer simulations produce more reasonable head profiles than two-layer simulations (Fig. 4). For example, the 29.7 kyr BP simulation, with a hydraulic conductivity of 0.05 ms–1 for the drainage layer, caused pore-water pressures to be below the overburden pressure and resulted in approximately 14% of the meltwater evacuating through the sediment layer. When the ice is at its maximum extent (29.7 kyr BP) the sediment layer contributes minimally to the removal of basal meltwater (Table 2). This percentage may represent the maximum volume that the aquifer is capable of transmitting through the fjord, illustrating that the majority of basal meltwater during this glacial stage must have been diverted through some interfacial drainage system. During the early advance stages, the total volume of meltwater entering the system is less than at the maximum, and the sediment layer transmits more of the basal melt, but is still incapable of evacuating all the meltwater. As in the two-layer model experiments, initial runs of the three-layer model for the 14.5 kyr BP ice-margin position only considered the basal meltwater contribution. When recharge is increased to account for surface melt, the sediments can then only transmit ~9% of the total volume of meltwater entering the system, under the constraint that the pore-water pressure cannot exceed the overburden pressure.
Table 2. Values for the six ice-margin positions in the three-layer simulations. The percentage of water traveling through the sediment layer is given; remaining drainage occurs through the drainage layer. Hydraulic conductivities in the drainage layer are the minimum values from Table 1 that prevent ice flotation (i.e. with the pore-water pressure below the ice overburden pressure). Total meltwater values (entering the groundwater model as recharge) are derived from the ice-flow model of Reference Winguth, Mickelson, Larsen, Darter, Moellerand and StalsbergWinguth and others (2005)


Fig. 4. Profiles of the potentiometric surface from the three-layer model for each simulated ice position. The results for the three-layer simulations shown here are those in which the pore-water pressures are lower than the ice overburden pressures.
Discussion
Overall, most of our groundwater models show that the sediment layer in Nordfjord cannot evacuate all the meltwater entering the system. During model simulations the aquifer sediments are initially able to transmit all the basal meltwater during times of significant glacial retreat. Once surface melt is included, the aquifer becomes overpressurized.
Hydraulic conductivities of the sediment layer used in this study were ~10–4ms–1 (Table 1). If the hydraulic conductivities of the sediments in Nordfjord were lower, these groundwater models would produce qualitatively identical results since the resulting pore-water pressures for all the two-layer groundwater models are so high. It is reasonable to assume that a drainage system existed to help drain away meltwater and prevent flotation of the ice. The high pore- water pressures generated in the models suggest that additional drainage must have been available. A study by Reference HindmarshHindmarsh (1999) illustrates that marine-based ice sheets terminating on fine-grained shelf sediments would not have been able to discharge all the meltwater through the bed. Hydraulic inefficiency of the bed could also initiate the formation of tunnel valleys, which would provide a means of catastrophic drainage of the pressurized subglacial water.
Conclusions And Wider Implications
The groundwater models for all the ice-margin positions (32, 30.5, 29.7, 27.5, 21 and 14.5 kyr BP) show that the sediment layer underlying the ice would not have been capable of transmitting all the meltwater through the fjord. Model results indicate that the groundwater system could carry only 14–38% of the basal meltwater produced during all but the latest stage of ice retreat, when it could carry only 9%. The glacial retreat groundwater model for 14.5 kyr BP shows that the sediments could have easily handled all the basal meltwater, but when surface melt is included in the simulation, groundwater flow through the sediment layer is no longer sufficient to evacuate all the meltwater. These results indicate that other paths of basal drainage were present during advance and retreat of ice in Nordfjord.
Studies involving direct measurements of hydraulic head in subglacial till indicate that typical subglacial water pressures can indeed be quite high. An early study by Reference MathewsMatthews (1964) estimated subglacial water pressures in British Columbia, Canada, to be within 50% of the ice overburden. More recently, Reference Hooke, Laumann and KohlerHooke and others (1990) demonstrated that subglacial water pressures were 50–75% of the ice overburden at Austdalsbreen, Norway, and Storglaciären, Sweden. If these measurements can serve as analogues to fjord ice, they provide support for the high pore-water pressures of the three-layer groundwater models in this study.
Similarly, the effects of high water pressure are observed in sediment beneath the Cordilleran ice sheet. Reference Brown, Hallet and BoothBrown and others (1987) showed that only a small portion of the basal meltwater could have been evacuated through the sediment underlying the last glacial Puget Lobe of the Cordilleran ice sheet owing to a widespread basal decoupling by subglacial water that was pressurized to the ice flotation level, producing lenses and layers of sand in till, and little overconsolidation of subglacial clays.
Subglacial water has a profound influence on ice-flow velocity, glacier stability and sediment erosion, transport and deposition. The episodic surging of some glaciers can be attributed to temporal changes in subglacial hydrology (Reference Fountain and WalderFountain and Walder, 1998). It is then possible that the high pore-water pressures deduced from this study could explain non-climatically driven margin readvances of the ice sheet.
Acknowledgements
We thank E. Larsen, A. Nesje, K. Stalsberg, J. Darter and L. Hansen for assistance in Nordfjord and for constructive comments on the project. This research was funded by US National Science Foundation grant EAR-0087369 (C. Win- guth, D. Mickelson and C. Moeller) and the Norwegian Research Council through the NORPAST project (E. Larsen).








