Heat Exchange over a Melting Snow Surface

Abstract

The relative importance of the principal elements of the thermal balance above snow during a period of melting has been evaluated using recent studies of the turbulent transfer in the boundary layer. Several anomalies in the profiles prove the continuing presence, near to the surface, of a thick layer of air apparently re-heated by the radiative flux. It is shown that the upper surface of this “exchange layer” ought to be considered as the new level for the origin of profiles, and taken as the exchange surface. The importance of nocturnal refreezing has been quantified. Excellent correlations have been found between mean air temperature and total energy balance; they have allowed the establishment of an approximate, non-linear expression for the effective daily ablation of snow as a function of mean air temperature. This relation gives satisfactory results at high and intermediate altitudes, in horizontal uncovered terrain. The measurements were made in the French Alps at 3550 m and in Spain at the latitude of Madrid à 1860 in.

On a évalué l’importance relative des principaux éléments du bilan thermique au-dessus de la neige en période de fonte, d’après de récentes études sur les transferts turbulents dans la couche limite. Diverses anomalies dans les profils prouvent ta présence continuelle, près de la surface, d’une épaisse couche d’air réchauffée vraisemblablement par le flux radiatif. On a montré que la face supérieure de cette “couche d’échange” devait être considérée comme nouveau plan des origines des profils et prise comme surface d’échange. L’importance du regel nocturne a été chiffrée. On a trouvé d’excellentes corrélations entre températures moyennes de l’air et bilan total d’énergie; elles ont permis d’établir une expression approchée, non linéaire, de l’ablation quotidienne effective de neige en fontion de la température moyenne de l’air. Cette relation donne des résultats satisfaisants à haute et moyenne altitude, en terrain horizontal et découvert. Les mesures ont été faites dans les Alpes françaises à 3550 m et en Espagne sous la latitude de Madrid à 1860 m.

Zusammenfassung

Die Hauptelemente der Wärmebilanz über schmelzendem Schnee wurden auf Grund neuerer Untersuchungen über den turbulenten Austausch in der bodennahen Schicht in ihrer relativen Bedeutung bestimmt. Verschiedene Anomalien in den Profilen beweisen das ständige Vorhandensein einer dünnen Luftschicht dicht über der Oberfläche, die wahrscheinlich durch den Strahlungsfluss erwärmt ist. Es wird gezeigt, dass die obere Grenzfläche dieser “Austauschschicht” als neue Ausgangsfläche für Profite betrachtet und als Austauschflâche gewählt werden muss. Das Ausmass des nächtlichen Wiedergefrierens wurde zahlenmässig erfasst. Zwischen der mittleren Lufttemperatur und der Energie-Gesamtbilanz ergaben sich engste Korrelationen; sic ermöglichten die Ableitung eines nichtlincaren Näherungsausdrucks für die tägliche effektive Schneeablation als Funktion der mittleren Lufttemperatur. Diese Beziehung liefert in grossen und mittleren Höhen bei ebenem und offenem Gelände befriedigende Ergebnisse. Die Messungen fanden in den französischen Alpen auf 3550 m und in Spanien auf der Breite von Madrid in 1860 m statt.

I. Introduction

In the thermal balance above a surface, the determination of the flux of sensible and latent heat is made indirectly, by measuring gradients, and with an uncertainty which is considerably greater than that which is introduced by measurement errors alone: in effect, the calculation supposes, on the one hand, that the air is in a neutral state, that is to say that the wind velocity profiles are logarithmic, and, on the other hand, that the turbulent exchange coefficients of momentum, of sensible heat, and of water vapour, are identical. The first hypothesis is rarely true above ice or snow in a period of melting, the air being in general stable; as to the second, it seems nowadays to be false. This is why, with the aid of recent results obtained on the mechanism of transfer, one is anxious to obtain general relations which allow us to calculate these fluxes taking account of the state of stability of the air.

II. Determination of the Flux of Sensible and Latent Heat

The shearing τ of the air layers (which can be interpreted as a vertical flux of momentum), the flux of sensible heat H and of water vapour W are supposed to be functions, respectively, of the mean gradients of horizontal wind velocity of temperature θ and of specific humidity Q:

(1)

where z, p and c_p are the height, the air density, and the specific heat capacity; K _m, K _h and K _w are the turbulent exchange coefficients of these three quantities. It is generally assumed that within the boundary layer τ, H and W are independent of z.

The Prandtl mixing theory leads to wind velocity profiles which are logarithmic, which is not observed in practice except when the air is adiabatically neutral, that is to say when the Richardson number (Ri) is zero where

(2)

Γ being the adiabatic lapse rate. Prandtl’s hypothesis is therefore that

(3)

being the friction velocity and k Kârmân’s constant. To take account of the profile shapes when (Ri) is different from 0, Monin and Obukhov (1954) have proposed the relation:

(4)

assuming that the function

necessarily dimensionless, can be approximated by an expression of the form:

(5)

α being a universal constant to be determined and L stability length, a quantity with the dimensions of length, independent of z, and such that

(6)

One obtains, after integration, the well-known expression:

(7)

Neglecting molecular transfer in comparison with turbulent transfer, one shows that if u’, w’, θ’ and q’ are respectively the instantaneous fluctuations around a mean value of the horizontal component of the wind speed u, of its vertical component w, of the air temperature θ and of its specific humidity q, at the same point, then:

(8)

The recent availability of instruments possessing the very small inertia necessary to measure these fluctuations allows one today to determine directly the intensity of the vary to various duxes with an acceptable precision. It is therefore possible to study experimentally the shape of the function

for a very large range of values of z/L or of (Ri).

This procedure has been extended to measurements of temperature and water vapour pressure (see Miyake and others, 1970). Starting from H and W, one can define the magnitudes θ* and q* having the dimensions respectively of a temperature and a specific humidity and independent of z in the boundary layer as is the friction velocity:

(9)

One then obtains the dimensionless equations:

(10)

(11)

z being the height at which one has measured the gradients and the Richardson number. Whereas the shape of the functions φ_m and φ _h are beginning to be well-known, we possess few reliable results concerning φ _w because of the peculiar difficulties, presented by the direct measurements of water vapour flux.

Since 1957, numerous experimenters (see Lumley and Panofsky, 1964) have shown that in the case of instability

and

, Dyer and Hicks 1970) give γ = 16 for —1 < z/L < —0.01.

Webb (1970) has found that in the neighbourhood of neutrality, for —0.03 < z/L < + 1, the law of Monin and Obukhov is reasonably verified and that

with α = 4.5 if z/L < o and α = 5.2 if z/L > 0. For very strong stabilities (+ 1 < z/L < 1 + α) he finds that the profiles become logarithmic again and that

.

The determination of the fluxes H and W therefore returns to a measurement of

and at two levels z₁ and z₂ the height z of a calculation of the gradient being such that, for for example:

(12)

III. Apparatus

The total radiation balance has been measured directly with a thermopile with a bismuth telluride-copper thermocouple, blackened and ventilated on its two faces in a current of air of so m s⁻¹ to avoid accumulations of snow and to minimize the asymmetric effect of wind. It is placed at 1.5 m from the surface and its sensitivity is 10.6 μV W⁻¹ m² , the absolute precision being better than 10%.

The measurements of wind speed, air temperature and water vapour pressure are made simultaneously at four levels: 0.25 m, 0.5 m, 1 m and 2 m. The anemometers and the thermometric elements give impulses whose frequency is a function of the intensity of the measured quantity. Mean values over 10 min are obtained directly every hour by counting the impulses during this lapse of time. A programmer assures the course of the sequence of measurements and the recording of the results.

The anemometers with a mean precision of the order of 0.05 m s⁻¹ have a lower limit of 0.3 m s-1. The four cup anemometers arc mounted on fixed horizontal arms and perpendicular to the direction of the principal wind. Infrared radiation emitted by 500 W resistances assure efficient defrosting without perturbing the measurements. Air temperatures are taken by aspiration; the thermistors of the thermometric elements are placed along the axis of two concentric silvered tubes through which a current of 1.5 m s⁻¹ is circulated; the accuracy is about 0.05 deg. For the measurements of vapour pressure, psychrometers arc used which re-heat the aspirated air to + 15° C to avoid freezing in the wet thermistors; in this way the mixing ratio is not changed. The air speed near the thermometric elements is 3.5 m s⁻¹ and the precision is estimated at 0.1 mbar. The apparatus is operated on 220 V A.C. single phase.

IV. Thermal Balance of the Vallée Blanche

Deformations of the profiles

The site chosen was at the top of the Vallée Blanche at 3550 in a.s.l., in the Mont-Blanc Massif (Fig. 1). Round the measurement station there was a vast snow field with very little relief and remarkably free of obstructions. The equilibrium line in this region is at about 2750 m and the annual balance at the measuring station is 3 m a⁻¹ (water equivalent). The measurements selected are those for the month of July 1968.

Fig. 1. Location of field station in the Vallée Blanche.

Fig. 2. Wind-speed profiles in the Vallée Blanche (July 1968).

In the majority of cases, the wind-speed profiles present at their base a reversal of slope (Fig. 2) which can be attributed to the macro-turbulence created by the undulations of the surface of the snow. These undulations, of small height but large dimensions (ten or so metres on average from one summit to the next) are caused by drift; they are not visible except in grazing light at sunset. At the base of the temperature profiles, one finds again a similar deformation to that observed in the wind-speed profiles, which proves the permanent presence of a layer of “warm” air in the first 50 cm above the snow. The re-heating is probably due to an intense absorption of the infrared by the water vapour in the air, but no measurement of divergence of radiative flux has yet been made in this region. Above this “exchange layer”, the mean daily value of (Ri) calculated between 0.5 and 2 m is equal to 0.060 with a variation given by a σ of 0.050; that of (Ri) at night is equal to 0.076 with σ = 0.0060 showing hat the air is a little more stable at night; the minimum (Ri) are rarely negative (Fig. 3). The parameter β of Deacon’s (1949) power law:

(13)

which, according to the well-known shape of the curve β = f (Ri) should be below unity is here on the contrary, continuously above. To correct this anomaly, one has allowed that the origin of profiles usually at the level of the snow, is to be found at a height Δz above the surface This height is chosen in such a manner that, according to the law of Mourn and Obukhov, the ratio of the differences of velocities at 0.5, 1 and a m

is compatible with the measured (Ri) (Fig. 4):

(14)

where

Fig. 3. Maximum, minimum and average (Ri) values, calculated between 0.5 and 2 m, for days (D) and nights (N) in the Vallée Blanche (July 1968).

Fig. 4. Variations of Δz with ratio of wind-speed differences far (Ri) values between -0.03 and 0.17.

Fig. 5. Frequencies of Δz values between o and 50 cm from wind-speed, vapour-pressure and air-temperature profiles, for logarithmic law.

The mean value found for the 25 profiles is 43 ± 9 cm. Assuming its profiles are logarithmic ((Ri) = 0 or L = ∞, one obtains

. Taking account of the precision of measurements, these values are not very different and it is possible to consider the logarithmic approximation as sufficient. This is what has been done, not only for the wind velocity profiles u, but also for those temperature θ and vapour pressure f. The mean values found are respectively 30 cm for u, 34 for θ and 32 for f. The means and variances are not significantly different at the 0.05 level, at least for the wind and the temperature (Fig. 5); assuming therefore that the Δz of the three magnitudes are simultaneously equal, one can consider the new level for their common origins as the exchange surface. Then the calculation of the fluxes is simply made by changing the variable from z to z — Δz A good study made in August 1970 at the same place (8 anemometers and 5 thermometric sounds from o to 2 m) has allowed the discovery above the snow of an air stratification in three superposed layers; the lower of 20 cm thickness and the next can go as high as 70 cm (Fig. 6).

Fig. 6. Wind-speed and temperature profites in the Vallée Blanche (August 1970).

The balances

Summer 1968 was particularly bad in the Alps. Air temperatures were cool and snowfalls abundant. Damage caused by the numerous storms (successive destruction of several thermistors, of a transformer and of a voltage regulator) obliged us to declare only the period from 1 to 25 July to be considered as reliable.

Contrary to the usual practice, it seemed clearer to us to count as positive the energies which contribute to the melting of snow or to re-heating. We have called “diurnal” events which occurred during the period of the day when the net radiation balance is positive (on average between 8 and 18 h) and “nocturnal” the others.

Mean hourly values of radiation balance and their standard deviations for a day and a night without clouds are: 0.59 ± 0.08 MJ m^-2 and - 0.31 ± 0.02 MJ m^-2. Fluxes of sensible and latent heat, H and L_SW, have been calculated hour by hour; their small contribution to the total balance is due to the fact that (Ri) is positive. Table I gives the diurnal and nocturnal values. If one had used the classical expressions derived from the logarithmic law, the values would have been two or three times more important. In day-time, H and L_SW each represent about 5% of the magnitude of the total balance and, because they approximately compensate each other, the radiation balance R represents practically 100%; in night-time they each represent 10% of the total and R 100% for the same reasons (Fig. 7). The radiations therefore have a very considerable role at this altitude. The mean gradients being very small, the precision in the calculation of the hourly flux of latent and sensible heat is only mediocre, but a large part of the error is random and the precision over a long period is certainty much better. The uncertainty in the diurnal or nocturnal total balance is about 15 to 20% (Table II).

Table I The Various Diurnal and Nocturnal Fluxes and Mean Air Temperatures at 2 m in the VallÉe Blanche in July 1968

The daily effective ablation is determined by weighing vertical cores of snow, according to the method described by LaChapelle (1959). The length of the cores is always above 0.5 m and is equal to that of the part of the reference slake which is under snow. Measurements are made, as far as possible, each morning before the beginning of melting. Aeolian erosion being negligible, one presumes that the difference in mass between two specimens taken at 24 h interval corresponds to the mass of snow melted in the day reduced by that of the water refrozen during the night. The estimated temperatures of the surface snow being slightly negative at night, one can consider, to the precision of the measurements, that the quantity of capillary water refrozen corresponds to the nocturnal balance. For the diurnal melt calculated over the whole period of measurement a value of 27.3 + 4.1 g cm ² was found, as calculated refreezing: 12.9 + 2.0 g cm ² and as measured ablation: 15.6 ± 1.5 g cm ^–2. The calculated evaporation in the course of this period representing 27.3 + 4.1 g cm ² one has 13.9 g cm² measured melt against 14.4 g cm² of effective calculated melt, which is not significantly different. About 50% of the diurnal melt on average is thus refrozen during the night.

Fig. 7. Diurnal (above) and nocturnal (below) heal fluxes in Ike Vallée Blanche (July 1969).

Table II Total Values for Various Balances During the Measurement Period in the VallÉe Blanche

Correlations

Among all the correlations which have been investigated, the most interesting are the following:

A linear correlation between nocturnal mean temperature at 2 m θN₂, and net nocturnal radiation balance R _N For 19 pairs the coefficient of correlation, equal to 0.71, is very significant at the 0.01 level; one finds as the regression law:

(15)

A linear correlation between mean nocturnal temperature at 2 m θN₂, and total nocturnal balance B _N For 19 pairs, the correlation coefficient, equal to 0.64, is also significant al the O.O1 level; the regression line is such that:

(16)

This expression permits a rapid evaluation of the nocturnal refreezing; it shows that the radiation balances and the total nocturnal balances are the more negative the higher the nocturnal mean temperature. In effect one has recorded at night-time lower temperatures on average in cloudy conditions; therefore the long wavelength radiations emitted by the cloud opposing those emitted by the snow give a smaller balance in absolute value.

A linear correlation between mean diurnal temperature at

and net diurnal radiation balance R _D. For 22 pairs the coefficient correlation is excellent, 0.90; the regression line is:

(17)

The distribution of points shows a distribution of exponential shape: a linear correlation between In (R _D) and

, gives therefore for 19 pairs (+ 3 aberrants) a coefficient even better: 0.94. From the regression line one deduces:

(18)

One observes (Fig. 8) that the diurnal radiation balance, positive between 8 and 18 h on average, reduces as the temperatures decreases, without ever becoming negative. The choice of an exponential function having for asymptote the temperature axis is therefore more logical than that of a straight line (Fig. 9).

A linear correlation between mean diurnal temperature at 2 m,

, and total diurnal balance B _D For 22 pairs, the correlation coefficient of 0.91 is also excellent; the regression line is:

(19)

For the same reasons as above a linear correlation between In (B _D) and

, has been tried; the results are shown in Figure 10. For 19 pairs (+ 3 aberrants), one obtains a correlation coefficient 0.97, that is to say even better; and one deduces:

(20)

Because of nocturnal refreezing, we have seen that the effective daily ablation ought to be calculated beginning from the total balance over 24 h. Although since there exists a good correlation between mean diurnal temperature and mean nocturnal temperature (coefficient 0.96 for 19 pairs), one can find an expression allowing the evaluation of daily effective ablation h beginning only from mean temperatures during the day-time (Fig. 11):

(21)

This approximate expression does not allow us to find the value of

for which h is zero, that is to say below which refreezing always compensates melting, but taking the mean daily value of the total nocturnal balance (-2.3 MJ m⁻²) instead of the regression law

, one obtains h = o when

.

Equations (21) used for the periods considered gives an effective melt of 12.3 g cm⁻² against 13,9 g cm⁻² measured.

Fig. 8. Diurnal (above) and nocturnal (below) radiation net fluxes in the Vallèe Blanche (summer 1968).

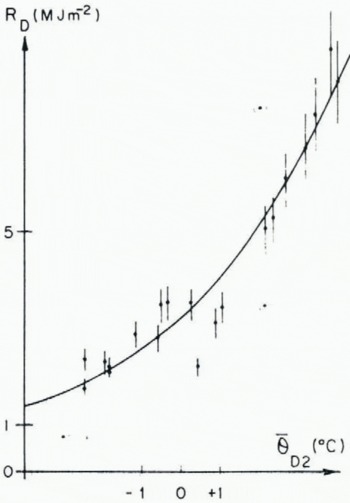
Fig. 9. (left) Non-linear correlation between average diurnal air-temperature at 2 m and diurnal radiation balance in the Vailèe Blanche (July 1968).

Fig. 10. (right). Non-linear correlation between average diurnal air temperature at 2 m and diurnal total heat balance la the Vallée Blanche (July 1969).

Fig. 11. Variations of actual ablation of snow, in 24 h, with average daily air temperature at 2 m.

V. Thermal Balance of the Sierra De Guadarrama (Castile)

Situation

The Sierra de Guadarrama (Fig. 12) is a mountain range oriented SW NE some 50 km north-west of Madrid, Spain. The summits exceed 2000 in and the snow can persist until July. In spring, the sudden arrival of warm, stable weather after a long period of cold causes rapid melting of the snow cover; the phenomena are therefore peculiarly suitable and easy to observe. The site chosen was the meteorological station of Puerto de Navacerrada (1860 m a.s.l.) where the apparatus previously used on the Vallée Blanche was installed, with some improvements; it was in the form of an enclosed area some 50 m². The masts supporting the measuring instruments were disposed in a manner in which they were not in the lee of any voluminous obstacle.

Fig. 12. Location sketch-map of field station in the Sierra rie Guadarrama.

Three principal oscillations of the air température have been revealed; the snow in the neighbourhood of the masts, some 50 cm thick on 5 April, had completely disappeared in the course of the first; however until at least May, 50% of the surface of the region remained covered. The complete measurements lasted from 12 April to 9 May. The later reduction was donc on a computer using the sign conventions mentioned in the previous paragraph.

Results

The measured values of the net radiation balance seem curiously little affected by the presence or absence of snow under the radiation balance meter; the mean hourly fluxes of the days and the nights without clouds are: 2.14 ± 0.05 MJ m^- and - 0.44 ± 0.04 MJ ^- with snow and 2.17 ± 0.01 MJ m ^- and - 0.49 ± 0.05 MJ ^- without. It is probable that the snow scattered with vegetable debris possesses an albedo close to that of the ground which is fairly clear.

The calculated Richardson number between 0.5 and 2 m over the whole period varies from —1 to +1, the air being on average unstable in the day

and stable at night

. The fluxes of sensible heat and water vapour have been calculated hour by hour; one notes that they do not become important except between 8 and 18 h, H being negative in the night (Table III) ; Figure 13 gives the values, mean for 28 d, for each hour.

To calculate the latent heat flux, the heat of sublimation of ice has been used or the heat of evaporation of water according to whether snow was present under the masts or not. Table IV shows that this distinction is not superfluous.

The relative importance of the fluxes of sensible heat and above all of latent heat is noticeably greater than in the Alps at 3550 m a.s.l. in that they represent, in absolute value, respectively 12% and 66% of the net radiation balance (Fig. 15). Because of the strong gradients measured at Puerto de Navacerrada, the accuracies are greater.

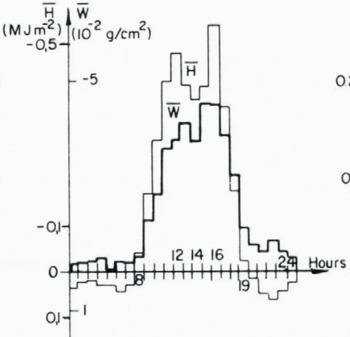
Fig. 13. (left). Hourly average valves for 28 d, of sensible-heat and water-vapour fluxes in the Sierra de Guadarrama (April, May 1970).

Fig. 14. (right). Hourly average values for 28 d, of Richardson number calculated between 0.5 m and 2 m in the Sierra de Guadarrama (April, May 1970).

From 12 to 15 April 9.50 g cm⁻² ablation was measured; taking account of evaporation which occurred during the same period, the effective measured melt is 8,9 g cm⁻². Nocturnal calculated refreezing being 3.5 g cm⁻¹, the effective melt is calculated at 7.6 g cm⁻²; this value is in reasonable agreement with the above, to the precision of the measurements. The refreezing therefore here represents about 30% of the total of the diurnal melt water.

When the wind is sufficiently strong and the sky is clear, no particular anomalies reveal themselves in the velocity profiles between 0.25 and 2 m; on the contrary, by day, when the air temperature is positive, (Ri) is negative above 0.5 m and positive below, the snow remaining at 0° C. One must conclude that H changes sign at this level. Assuming that we have a conservation of water-vapour flux and of total flux of heat, one deduces that the air layer between 0 and 1 m absorbs a certain percentage of the radiation for which it restores the energy by turbulent transfer. An evaluation of H above and below 0.5 m by the method of gradients shows that we have between 7 and 10% of the radiative balance absorbed in the day and o to 3% at night. There, furthermore, the high water-vapour content of the air above the snow must be the cause.

Table III The Various Diurnal and Nocturnal Fluxes and Mean Air Temperatures at 2 m in the Sierra De Guardarrama in April and May 1970

Table IV Diurnal and Nocturnal Means of the Various Balances in the Sierra de Guardarrama

Fig. 15. Diurnal and nocturnal heat fluxes in the Sierra de Guadarrame (April, May 1970).

Correlations

The same correlations have been tried as on the Vallée Blanche. The linear correlation between mean nocturnal temperatures at

, and nocturnal radiation balance R _N is significant at the 0.01 level. One obtains for 27 pairs a regression line comparable to that obtained in the Alps:

(22)

Because of the great relative importance of the fluxes of H and W, which results in a large inaccuracy in the determination of the total balance, no significant correlation has been found between these total balances and the temperatures. On the other hand, the linear correlation between mean diurnal temperatures at 2 m,

and diurnal radiation balance R _D is significant at the 0.01 level, the regression line found for 27 pairs being:

(23)

These values are, probably because of the low snow albedo, much larger than in the Alps. We note that here the choice of an exponential function does not improve the correlation coefficient.

We have seen that the conditions of snow melt here are very different from those observed in the Vallée Blanche. It has nevertheless seemed interesting to test Equations (21) of section IV giving a value for the magnitude of effective daily melt as a function of the mean diurnal air temperature alone; in the period from 6 to 15 April we measured 13.1 g cm⁻² of pure melt of which a small unknown quantity is due to light rainfall. The approximate expression gives 10.2 g cm⁻²; we can thus estimate that it gives acceptable indications even at lower altitude.

VI. Conclusion

We conclude by remarking that, to the extent that the two experiments can be compared, a decrease in all the terms in the balance with altitude has been observed, and an increase of the importance of the net balance of radiation relative to the fluxes of sensible and latent heat. It is to be hoped that this study of thermal balance above snow in a melting period will contribute to the improvement of methods of systematic measurement and calculation of fluxes over ground, as well as to show the important role, nevertheless difficult to evaluate, of well-known phenomena such as the nocturnal refreezing or the divergence of radiative flux. We must not finally forget, that the results obtained depend essentially on studies still in progress on the real shape of the functions

principally where the water-vapour flux is concerned.