1.Introduction
The growth process of ice dendrites from supercooled water has been studied for many years, because it was considered by metallurgists as a typical case of dendritic growth, and useful comparisons could be made with the features observed in other substances. Furthermore, the interest in ice dendrites has increased recently, due to their importance in problems of atmospheric physics. Several works have been published on their growth modes and velocity (Lindenmeyer, unpublished;Reference Lindenmeyer and ChalmersLindenmeyer and Chalmers, 1966; Reference HallettHallett, 1964; Reference Macklin and RyanMacklin and Ryan, 1965, 1966,1968; Reference PruppacherPruppacher, 1967[a], Reference Pruppacher[b]).
Special characteristics of these dendrites are their development as planar dendrites and their splitting and changes of orientation, which occur with increasing supercooling. According to Lindenmeyer (unpublished) andReference Macklin and RyanMacklin and Ryan (1968), the direction of the dendrite a-axis should coincide with that of the resultant of the growth velocities Va and Vc in the direction of the a- and c-axis respectively. This would be the direction of maximum growth velocity, given by:
where α represents the inclination of the dendrites with respect to the basal plane. The increase of the angle α with the supercooling would then indicate an increase of the velocity ratio Vc/Va.
This interpretation is not, however, directly supported by the theory of dendritic growth (Reference Bolling and TilleBolling and Tiller, 1961). Actually, according to this theory, dendrites should have their a-axis in the direction of maximum growth velocity which simultaneously satisfies a condition of symmetry at the tip of the dendrite with respect to the crystalline structure. Then, as long as Va > Ve, the a-axis of the dendrites should coincide with the a-axis and the increase of Vc/Va should only result in an increase in the dendrite thickness with respect to an ideal dendrite grown at the same supercooling.
In the present paper a mechanism is proposed to explain the splitting and inclination of ice dendrites which takes into account the hypothesis of Lindenmeyer and of Macklin and Ryan and also the theory of Bolling and Tiller.
For clarity, the experimental observations of the phenomenon and some points of the theory will be summarized below.
2.Experimental evidence
(a) Growth velocity in the direction of the a-axis.
This velocity has been studied by several authors as a function of the bath supercooling ΔT, and slightly different results have been obtained (Lindenmeyer, unpublished; Reference Lindenmeyer and ChalmersLindenmeyer and Chalmers, 1966; Reference HallettHallett, 1964; Reference Macklin and RyanMacklin and Ryan, 1966, 1968; Reference PruppacherPruppacher, 1967[b]). Following Pruppacher, Va can be expressed as
The curve of Va(ΔT) has been compared by Pruppacher to the corresponding theoretical curve, calculated by Reference Bolling and TilleBolling and Tiller (1961). He shows that both curves might coincide if an interface supercooling (δT i)a is supposed to exist at the tip of the dendrite, and he concludes that, in the range of temperatures investigated (0° to –18°C), two intervals may be considered, so that
In terms of the molecular mechanism of growth, the first interval should correspond to growth by lateral spreading of steps and the second to the continuous growth regime.
(b) Orientation of dendrites with respect to the basal plane.
According to the measurements of several different authors (Lindenmeyer, unpublished; Reference Macklin and RyanMacklin and Ryan, 1965, 1966, 1968; Reference PruppacherPruppacher, 1967[a]), the dendrites split, for ΔT > 1–2°C, in symmetrical branches, forming between them an angle 2α, which increases with ΔT and which tends to a limiting value 2α = 45° for ΔT > 9 deg. This was shown specially clearly by Pruppacher, who extended his measurements down to Δ7= 14 deg. For larger supercoolings direct measurements of 2α were not possible.
However in one case Reference HallettHallett (1964) was able to measure the growth velocity of dendrites in the direction of the c and a axes at ΔT = 16 deg and deduced α = 38° at this supercooling. Furthermore there is indirect evidence that 2α should increase for ΔT > 14 deg. It has been shown byReference Levi, Aufdermaur, Riehl, Riehl, Bullemer and EngelhardtLevi and Aufdermaur (1969) that, when ice structures formed by accretion and freezing of supercooled droplets are obtained with a surface temperature < 0°G, the crystal c-axes tend to be oriented in the direction of growth, when the temperature of the air and of the arriving droplets are in the range 0 > ta > –8°C. At colder temperatures (−8 > ta > > −15°C) the c-axes form with this direction an angle 10° < φ < 30°, while they form an angle φ = 45° for ta = –18 or –22°C.
These different orientations of the crystal c-axes have been related to the different crystallographic orientations of the dendrites grown during the initial freezing of supercooled droplets. Then the value φ = 45° obtained for the lowest temperatures would indicate that α also reaches the same value for a temperature in the interval indicated above.
3.General theory of dendritic growth
It is known (Reference Bolling and TilleBolling and Tiller, 1961) that, for an ideal dendrite, the dendrite cap would be limited by an isothermal surface with the shape of a paraboloid of revolution. The conditions of optimization of the growth velocity Vindicate that the radius of curvature of the tip, ρ/2, must satisfy the equation
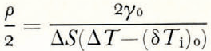
where ΔT and (δT i)0 are the bath and the interface supercooling respectively, ΔS is the entropy of fusion for unit volume and γ 0 is the surface free energy. Since the product Vρ is approximately constant for a given supercooling, if ρ increases according to Equation (5), then the velocity V decreases.
It may be seen from Equation (5) that, for the maximization of V, the preferred direction with respect to the crystalline structure will be that which minimizes (δT i)0. On the other hand, if Vφ is the growth velocity in a direction forming an angle φ to the dendrite axis, it may be easily seen that, for the conservation of the tip shape, Vφ must be given by
where V 0 is the axial velocity.
Using V = μ(δT i) as the general law for the solidification mechanism, where μ is a coefficient which may depend on the temperature, Equation (6) may be written
where (δT i)0 and (δT i)φ are the interface supercoolings in the axial direction and in a direction forming the angle φ with this axis. These supercoolings are related by the expression
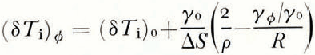
where γ 0 and γφ are the surface free energies in the axial direction and at an angle φ to the axis and R is the radius of curvature of the region of the surface characterized by the angle φ.
For an isothermal dendrite the radius of curvature R has the expression
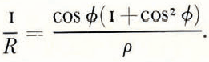
Since according to Equations (8) and (9) R > ρ/2 and (δT i)φ = (δT i)0 it also follows from Equation (7) that, for an isothermal dendrite, μφ ≤ μ 0 cos φ. When this condition is not satisfied, the surface of an isothermal dendrite becomes unsTable. Then, the radius of curvature at the tip should increase above the limit given by Equation (5). The dendrite would get thicker and the growth velocity lower.
4.Interpretation of ice dendrite characteristics
(a) Mechanism of splitting and irrational orientation of the dendrites.
We will consider an ice dendrite growing initially in the direction of the a-axis. It has been assumed by Bolling and Tiller that the tip of a dendrite should usually tend to be limited by low index planes. In the case of ice, these planes are {1010} and (0001), the latter containing the dendrite axis. Then two sides of the dendrite tip will be limited by two {1010} planes (φ = 60°), but the other sides, normal to the first ones, should be formed by higher index surfaces, each of them tending to a (0001) plane (φ = 90°) at some distance from the tip.
We see from Equation (9) that the radius of curvature R will tend to ∞ (1/R → 0) for φ → 90° and Equation (8) may be simplified to
Using Equation (5) this may also be written
From Equation (10′), (∆T i)90 is obtained easily, since the value of (δT i)0 corresponding to a given ΔT may be calculated by applying Pruppacher's results (Reference Pruppacher1967[b]) represented by Equations (3) or (4) and by the experimental curve of V as a function of ΔT (represented by Equation (2) for ΔT < 9°C). Some values of these supercoolings are given in the last columns of Table I. Here (δT i)0 and (δT i)90 have been represented by (δT i)a and (δT i)c respectively, to indicate the corresponding crystallographic direction. The Table shows that (δT i)c ≈ ≈ 3(δT i)a and that the ratio of these supercoolings varies very slowly with the temperature.
Table I. Growth velocities and interface superooolinos parallel. to in a- and c-axes

On the other hand, it may be observed from Equations (8) and (9) that the variation of (δT i)φ with the angle φ must be more pronounced for φ > 45° than in the vicinity of the tip. Actually, for φ < 45°, cos φ decreases slowly and yφ probably increases because the index of the surface increases; on the contrary, for φ > 45°, the variation of cos φ is faster and γφ should decrease, tending to a minimum value for φ = 90°. Then, in the region of large φ, where (δT i)φ increases rapidly, the approximately paraboloidal cap of the dendrite would become unsTable, and for Vc/Va larger than a given limit, a protuberance could be formed on the surface.
Now, since the radius of curvature at the tip of the protuberance will be smaller than that of the original dendrite, its growth velocity will be higher and the protuberance will overtake the dendritic tip. Then, if we start with an initially basal dendrite, two symmetrical instabilities will be formed at both sides of the tip and the phenomenon will determine the splitting of the dendrite.
After the splitting, the thermal interaction between the two symmetrical branches will hinder the splitting phenomenon on the inside surfaces and the instability effect will operate periodically only on the outside surfaces, determining the inclination of the dendrites. However, with the increase of the distance between the two advancing tips, the interaction will decrease and new splittings will take place, the more frequently the larger the value of α.
According to this interpretation, the growth direction of a dendrite would be the resultant of the advance of the dendrite lip in the direction of the a-axis and of its shifting in the direction of the c-axis because of the formation of lateral layers. Accordingly, Equation (1) would be maintained and, for a given bath supercooling ΔT, the velocity Vc could be obtained from Va (as indicated byReference Macklin and RyanMacklin and Ryan (1968)), by means of the expression
though the values of Vc and Va would correspond to different interface supercoolings.
(b)Effect of the temperature on the ratio Vc/Va.
In Table I Va and Vc have been calculated for several values of ΔT. Because of the uncertainty of the results in the range 9 ≤ ΔT ≤ 14 deg (Reference PruppacherPruppacher, 1967[b), the calculated points are taken in the interval 0 < ΔT < 9 deg, with the exception of the last point, at ΔT ≈ 18 deg.
As observed by previous authors (Reference HallettHallett, 1964; Reference Macklin and RyanMacklin and Ryan, 1966), the results show that, if only the bath supercooling is considered, Vc increases rapidly with respect to Va with increasing ΔT, reaching approximately the same value when ΔT approaches 18 deg. It could now be of interest to compare pairs of values of Va and Vc corresponding to the same interface supercooling. This may be done if we observe that, in Table I, (δT i)c for ΔT = 2 deg approximately coincides with (δT i)a corresponding to ΔT = 6 deg and similarly that (δT i)c for ΔT = 8 deg may be compared with (δT i)a for ΔT = 18 deg. Therefore
and we see that, if the same interface supercooling is considered, then, through the whole studied range, Vc ≤ Va, though the ratio of these velocities evidently decreases with increasing (δT i).
It should be noted that the values of α and Vc in the last line of the Table have been indicated as approximate; this, as mentioned before, is because of the uncertainty of the accretion experiments, and also because, if the present interpretation is correct, the value α = 45° would not correspond to a single value of ΔT but should remain constant over a certain temperature interval and possibly represent a limiting value. In fact, it is easy to see that α. > 45° could take place only when Vc > Va for (δT i)c ≤ (δT i)a, i.e. when the c- and a-axes interchange their role in the growth of dendrites. Then there would be an interval of temperatures where an increase of the ratio Vc/Va could only determine an increase of the dendrite thickness with respect to the theoretical thickness of isothermal dendrites at the same supercooling.
Experimentally it has been found in accretion experiments, that the orientation of the c-axis of crystals to the growth direction reached 45° at an air temperature of –18°C and remained at this orientation down to the lowest temperature of the experiments, –22°C in similar injection conditions. This result is in agreement with the above observation, though it must be noted that this interval of air temperature, of only 4 deg, may not be considered as a definitive proof of the effect under discussion.
(c) Dendrite width and thickness.
According to the mechanism of splitting and inclination of ice dendrites proposed here, the dendrite tip should always point with its region of maximum curvature in the direction of the a-axis. This is in agreement with the schematic representation proposed initially by Reference Macklin and RyanMacklin and Ryan (1965). However, later on (Reference Macklin and RyanMacklin and Ryan, 1966), the same authors assumed the dendrite tip was oriented as the main body of the dendrite. It may be noted that the latter hypothesis encounters some difficulty if the thickness of the dendrites is considered. In fact, since in this case, on increasing ΔT, Vc would approach Va for the same interface supercooling, the growth velocity should become of the same order of magnitude in all directions and the dendrites should increase in thickness, independently of their orientation (non-isothermal dendrites). On the other hand it is known (Reference PruppacherPruppacher, 1967[a]) that the ice dendrites become very thin on increasing the supercooling. Their thickness has not been studied in detail, but some measurements exist of their width in the basal plane (Reference HallettHallett, 1964), which may be used for comparison.
In the first column of Table II the width of the dendrites (secondary branches), obtained from Hallett's curves, is given for a few temperatures. From these values, the radius of curvature at the tip, ½ρ, has been obtained considering in the calculations the dendrite cap as a paraboloid of revolution and supposing that the width (= 2R) was measured at about 1 mm from the tip (as may be deduced from Hallett's figures). The results are represented in the third column of the Table (½ρ exp.). Finally the theoretical values of ½ρ, shown in the fourth column, were obtained byReference Bolling and TilleBolling and Tiller (1961), as an application of the theory of non-isothermal dendrites. The comparison of the figures in the third and the fourth column shows that the development of the ice dendrites in the basal plane is in approximate agreement with the theoretical results.
Table II. Radius of curvature at the tip of dendrites in the basal plane

Since these dendrites are, over the whole range studied, much thinner than they are wide, it follows that the theory of non-isothermal dendrites should not be applied to calculate their thickness and so Vc ≪ Va for the same interface supercooling, in agreement with the present interpretation.
(d)Modification of the angle at for ice dendrites growing in aqueous solutions:
The growth velocity and the angle 2α have been measured in aqueous solutions of several electrolytes by Lindenmeyer (unpublished) and by Reference PruppacherPruppacher (1967[a]) and in solutions of sucrose by Reference Macklin and RyanMacklin and Ryan (1966, 1968). The results are very similar. They show that the presence of a solute in water decreases the growth velocity and increases the angle 2α. The effect is nearly independent of the solute substance.
So, for electrolyte solutions of a concentration 10−1N, the limiting value of 2α (similar to the limit 2α = 45° for pure water) is shifted to 2α = 60°. This is reached for instance at ΔT = 4 deg and at ΔT = 6 deg for Na salts and for NH, salts respectively. Reference Macklin and RyanMacklin and Ryan (1968) do not give the angle 2α directly, but they plot the growth velocities Va and Vc as a function of ΔT. By comparing the curves the angle 2α may be calculated and the limit value is obtained again at 2α = 60° for a 10−1N sucrose solution (reached at ΔT ≈ 4 deg).
Macklin and Ryan also indicate that the initial temperature of splitting Δ T0 is increased for solutions as compared with pure water, being for instance ΔT0 = 1.2 deg for a 10−1N and ΔT 0 = 0.2 deg for a 2 × 10−1N sucrose solution (the same authors give ΔT 0 = 2.7 deg for pure water).
It is known that the inhibition of the growth velocity caused by the presence of a solute is related to the concentrated layer formed at the interface of the advancing tip (Reference Bolling and TilleBolling and Tiller, 1961) which reduces the melting point and consequently the effective interface supercooling with respect to the bath supercooling. Now, according to the interpretation of the splitting and inclination of dendrites proposed here, the concentration gradient existing near the dendrite tip could also be the cause of the increase of α. Actually, since the lateral growth is much slower than the advance of the tip, the concentration layer may get diluted along the dendrite body. Supposing this part of the dendrite can be considered as approximately isothermal, the interface supercooling should increase at some distance from the tip and consequently the effects of the lateral instabilities considered above should also increase.
This interpretation would explain why the effect depends very little on the particular substance used as a solute. It would also eliminate the contradiction observed by Reference PruppacherPruppacher (1967[a]) with the results obtained for ice growing in capillariesFootnote * according to which the growth velocity of ice in the direction of the c-axis, measured in other experiments, would be slightly inhibited by the presence of small concentrations of some electrolyte. In fact, this would be a minor effect compared with the change of the interface concentration along the dendrite body.
On the other hand, this kind of explanation could not be applied if the interpretation of the irrational growth of ice dendrites given by Reference Macklin and RyanMacklin and Ryan (1966) is accepted, because m this case the phenomenon would not be related to the different supercoolings existing at different points of the dendrite cap.
Conclusions
The results discussed above may now be used to obtain the law of the growth velocity of ice in the direction of the c-axis as a function of (δT i)c
In the interval of bath supercoolings 2 deg ≤ ΔT ≤ 8 deg,
The average exponent n of (δT i)c is slightly smaller in the last interval of Table I, 8 deg < < ΔT < 18 deg, where it is n ≈ 2.5.
According to the general theory of the molecular mechanism of growth, Equation (13) should correspond well enough in the interval of temperatures where the transitional growth regime prevails (n > 2 according to Reference Cahn, Cahn, Hillig and SearsCahn and others (1964)). This regime represents the transition between the growth by lateral spreading of steps (n = 2) and the continuous regime (n = 1).
As observed byReference HallettHallett (1964) and by Reference PruppacherPruppacher (1967[a]), previous results on the growth of ice in capillaries in the direction of the c-axis, for ΔT ≤ 1 deg, indicate that m these conditions the growth velocity increases much more slowly than predicted by Equation (13). Though the present and previous results are not strictly comparable because of the different growth methods used, this difference seems to indicate that the transition supercooling (δT i)c* between the growth by lateral spreading of steps and the transitional regime must be found near the low limit of Table I ((δT i)c* ≤ 1 deg). According to Pruppacher a similar transition in the direction of the a-axis should take place at (δT i)a* = 0.58 deg Then, it we do not discuss here the difference between the laws represented by Equations (3) and (13), and we admit that both of them may represent the transitional regime, in spite of the dînèrent exponent of (δT i), we should conclude that the transition temperatures depend very little on the growth direction. Consequently, since (Reference Cahn, Cahn, Hillig and SearsCahn and others, 1964)
where vs the molecular volume of the solid, Tm, the melting point, a, the step height L the latent heat of fusion and y are all constants, the parameter g, which is a measure of the diffuseness of the surface, should be approximately the same (g ≈ 10−2 according toReference PruppacherPruppacher (1967[b]), and the ice surface in contact with the liquid should be rather diffuse, irrespective of its orientation.
Acknowledgements
The author is grateful to D Fainstein for helpful discussions and to E. Achaval for reading the text.



