Analyses of the hydrographs for two successive jökulhlaups from glacier-dammed Summit Lake, British Columbia (Reference MathewsMathews, in press) show that instantaneous water discharge, Q t , is related not to time, t, since the start of each flood but to the volume of water, V t , released from the lake during this time. For all but the initial stages of the flood discharge can be expressed by a formula of the form:
(in which for Summit Lake K = 0.72 and b = 1.5 if Q t is expressed in m3/s and V t in m3 × 106). Equations of this same form apply to jökulhlaups from five other ice-dammed lakes, although the coefficient and exponent differ for each lake (Table I). Hydrographs for these floods, based on calculated or measured discharges plotted against cumulative volume lost, instead of time, are shown in Figure 1.

Fig. 1. Relation of cumulative volume drained during jökulhlaups and instantaneous water discharge. Equations are of the form Q t = K(V t )b, in which the coefficient, K, and exponent, b, for each flood are listed in Table I. The peak discharge for each jökulhlaup is indicated by a dot. E, Ekalugad Valley; Gj, Gjánúpsvatn; Gr, Graenálon; St, Strupvatnet; Su, Summit Lake; T, Tulsequah Lake.
Table I Jökulhlaup data: K and b, coefficient and exponent of Equation (1); H, height of lake surface above toe of ice dam; L, distance from lake to toe of dam; D, depth of lake at ice dam; V max, reservoir storage; Q max, maximum instantaneous water discharge. The jökulhlaups are historic except from Lake Missoula which is of late Pleistocene age. Floods resulting from volcanic activity are excluded. Some of the data were compiled by J. J. Clague from topographic maps and air photographs

Values of K and b for the six examples show large variations, with extreme values found at two British Columbia lakes, Summit and Tulsequah. Possible factors influencing these values include: the head loss, H, between the high-water mark in the reservoir and the toe of the ice dam where the escaping water generally emerges, the distance, L, from reservoir to point of emergence, the depth, D, of the reservoir at the dam, and the capacity, V max, of the reservoir (Table I). A plot of V max against the ratio H/L for the data in Table I indicates, as one might expect, that small reservoirs are in general impounded by dams with large height-to-length ratios. Likewise, K displays a negative relationship to V max, albeit a weak one. For a small dam the passage of 106 m3 of water (for this volume, Q t = K in Equation (1)) can be expected to generate a larger leak, a higher discharge, and hence a higher value of K than is the case for larger ice dams with generally smaller values of H/L. Thus the size of the dam may control both the available reservoir storage and the coefficient of Equation (1), and, accordingly, K and V max are not wholly independent of one another. However, the interrelationships of V max, K and H/L all show large scatter, far beyond that of the individual points on the rising curves of the hydrographs, and none of the other factors investigated can be clearly associated with variations in values of K and b.
In Figure 1 the peak discharge, Q max, occurring at the end of each jökulhlaup is designated by a dot. Curiously, all peak discharge values fall close to a common line despite the variations in slope and position of the individual hydrographs. Peak discharges for floods from four additional ice-dammed lakes are presented in Table I, and Figure 2 shows the resultant relationship between maximum flood discharge (in m3/s) and available water storage (in m3 × 106) for the ten lakes. The data points cluster about a line represented by:
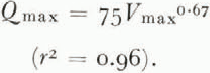

Fig. 2. Relation of total volume drained during jökulhlaup (V max) and peak water discharge (Q max); r 2 = 0.96. Dashed lines indicate 95% confidence interval for estimates of peak discharge (residuals are assumed to be normally distributed).
This relationship is a remarkably good one considering that the data include peak discharges measured at varying distances from the toes of ice dams and are derived from lakes of widely differing size and other characteristics.
More data from other jökulhlaups and from other ice-dammed lakes are clearly needed to clarify and explain the relationships, but in the meantime the log–log plot of Q t against V t is a useful tool for investigating jökulhlaups, and Equation (2) offers an empirical basis for estimating possible maximum discharges from self-dumping ice-dammed lakes.
Acknowledgements
This study was supported by the National Research Council of Canada. Drafts of the paper were critically reviewed by M. A. Church and O. Slaymaker.





