Introduction
The Arctic appears to play a crucial role during changes in global climate, both recent and past (e.g. Reference Alley, Smith and GrebmeierAlley, 1995). General circulation models indicate that increased greenhouse-gas concentration in the atmosphere may lead to climate warming, and that this warming may be most pronounced in the Arctic (e.g. Reference Houghton, Filho, Callander, Harris, Kattenberg and MaskellHoughton and others, 1996). Close monitoring of the Arctic climate is essential to test these predictions.
There are few weather stations in the Arctic, and the climatic interpretation of their records is hampered by large inter-annual variability, short record lengths, heat-island effects and unknown spatial representivity (e.g. Reference Kelly, Jones, Sear, Cherry and TavakolKelly and others, 1982; Reference Bowling, Weller, Wilson and SeverinBowling, 1991). A complementary approach to detect potential changes in the Arctic climate is to study corresponding changes in natural settings, such as on glaciers (e.g. Reference Cogley, Adams, Ecclestone, Jung-Rothenhäusler and OmmanneyCogley and others, 1995, Reference Cogley, Adams, Ecclestone, Jung-Rothenhäusler and Ommanney1996; Reference DowdeswellDowdeswell, 1995) or in permafrost (Reference LachenbruchLachenbruch, 1994; Reference Osterkamp and RomanovskyOsterkamp and Romanovsky, 1996). The remoteness of glaciers and the cumulative nature in which changes of their mass balance are displayed by their volume and length make them sensitive indicators of climate change. On the other hand, the climatological interpretation of short-term changes of individual glaciers can be difficult, because errors in mass-balance measurements can obscure existing trends and because it is not known a priori how representative a particular glacier is within a geographic region. Changes in glacier length are also complicated by glacier flow and there is a poorly understood time lag between changes in mass balance and terminus response (Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others, 1989; Reference Schwitter and RaymondSchwitter and Raymond, 1993; Reference EchelmeyerEchelmeyer and others, 1996).
In this paper we present annual and long-term mass-balance data from McCall Glacier, Alaska. This glacier is located in the northernmost glacierized region of the United States and its mass balance is directly influenced by climate change in this Arctic region. Short-term comparative studies on neighboring glaciers indicate that McCall Glacier is regionally representative. Furthermore, the successful modeling of its mass-balance record, using meteorological parameters from distant weather stations, implies a larger-scale representivity of this glacier’s mass balance.
Background on Mccall Glacier
McCall Glacier is located in the Romanzof Mountains at 69° 17′ N, 143°50′ W, close to the northern front of the northeastern Brooks Range (Fig. 1). The glacier is about 8 km long and has an area of 7.4 km2. Ice originates in three cirques, from east to west, Upper, Middle and Lower, and flows from an elevation of more than 2700 m to the present terminus at 1350 m with a mean slope of 8° (Fig. 2). Precipitation sources for the glaciers in this region are the Bering Sea, about 700 km to the west, and the Arctic Ocean, about 100 km to the north. Seasonal mass exchange on McCall Glacier is quite small: the current winter and summer balances are around 20 and –60 cm, respectively. Annual precipitation is about 0.5 m (Reference Wendler and IshikawaWendler and others 1974), more than half of which falls as snow. Reference Trabant and BensonTrabant and Benson (1986) showed that superimposed ice formation and internal accumulation are significant on the glacier, with the latter contributing more than 40% of the annual net accumulation. Because of patterns in mountain shading and wind deposition, the equilibrium-line altitude (ELA) is not well-defined; instead it spans an elevation range of 350 m in an average year (Reference Wendler, Ishikawa and StretenWendler and Ishikawa, 1974; Reference Trabant and BensonTrabant and Benson, 1986). The mean annual air temperature is about –12°C at 1700 m elevation. The near-surface and basal ice temperatures in the accumulation area are between –1° and –1.5°C (Reference Orvig and MasonOrvig and Mason, 1963). In the ablation area, surface-ice temperatures are less than –10°C, while the basal ice is temperate, at least near the center line (Reference Trabant and MayoTrabant and others, 1975).

Fig. 1. Existing glaciers between Hulahula and Jago Rivers, northeast Brooks Range. Numbers indicate glaciers that were surveyed between 1993 and 1995. The outline of the Okpilak Batholith, a large granitic intrusion, is shown as a dotted line.
Previous studies of the surface geometry and the mass and energy balance of McCall Glacier were made during the International Geophysical Year (IGY) in 1957–58 (e.g. Reference SaterSater, 1959) and during the period 1969–75 (e.g. Reference Wendler, Fahl and CorbinWendler and others, 1972, Reference Wendler and Ishikawa1974). Our continuing investigations began in 1993 (Reference Rabus, Echelmeyer, Trabant and BensonRabus and others, 1995) with measurements of surface and bed geometry, mass balance, meteorological variables, ice temperature and ice velocity (Reference Rabus and EchelmeyerRabus and Echelmeyer, 1997).
Definitions
It is important to set forth several definitions of the mass-balance terms used in this study. We follow those of Reference Østrem and BrugmanØstrem and Brugman (1991), with some changes in reference to Arctic glaciers.
The mass balance of a glacier can be measured using either Glaciological, topographical or hydrological methods. The Glaciological method involves measurements of local mass balance using poles and snow density in pits. These data are used to calculate the balance for a given hydrological year, either beginning and ending at a specified date (fixed-date system) or from one summer surface to the next (stratigraphic system). The topographical method compares two surfaces, defined by surveying the glacier (by photogrammetry or other methods) at two different times. To convert the calculated volume change to mass balance, one must assume a bulk density for the ι unknown) proportions of ice, firn and snow that are lost or gained. In contrast to the Glaciological method, in which systematic errors accumulate, the topographic method becomes more accurate when evaluated over a longer time span (Reference KrimmelKrimmel, 1989). Both Glaciological and topographical methods have been used on McCall Glacier (Reference Trabant and BensonTrabant and Benson, 1986; Reference Rabus, Echelmeyer, Trabant and BensonRabus and others, 1995). The hydrological method determines mass balance from precipitation and the discharge of an outlet stream. The geometry of the drainage basin and aufeis formation makes this method unfavorable for McCall Glacier (Reference Wendler, Fahl and CorbinWendler and others, 1972).
Two additional sources of accumulation, internal accumulation and superimposed ice, complicate mass-balance measurements on Arctic glaciers with their cold surface temperatures (e.g. Reference Wakahama, Kuroiwa, Hasemi and BensonWakahama and others, 1976; Reference Trabant and MayoTrabant and Mayo, 1985; Reference Trabant and BensonTrabant and Benson, 1986). Internal accumulation occurs by the refreezing of surface water that percolates below the previous summer surface into the firn and macroscopic features such as crevasses. Superimposed ice forms near the equilibrium line by refreezing of water on top of the last summer surface. Both contributions to the mass balance are considered by using the topographical method over sufficiently long time periods. In contrast, the Glaciological method, which usually determines the surface balance above the last summer surface, includes only superimposed ice. Internal accumulation must be estimated independently. We define the net balance as the sum of the surface balance and this internal accumulation.
Various methods can be used to calculate the balance for the entire glacier given the local pole balances. In the balance is elevation method, a low-order polynomial is fitted to the local balances vs elevation. The net balance is then obtained as a sum of interpolated local balances in successive elevation bands, weighted according to the area–elevation distribution of the glacier. In a different approach, a contour map of mass balance is constructed using two-dimensional interpolation of the local balances. Then numerical integration of the balance over the glacier surface gives the net balance. We call this the balance-map method; it can be implemented successfully only if the mass-balance network provides sufficient areal coverage.

Fig. 2. Maps of surveyed glaciers, with elevation contour interval of 100 ft (≈ 30.5 m). Elevation labels in meters are added where 100 ft contours coincide with 100 m contours to better than ± 5 m. North is upward. Tick marks representing UTM easting and northing are shown even 2 km. GPS profiles are shown as solid lines, with small solid symbols corresponding to individual point measurements; these appear as solid heavy lines for the continuous profiles. For McCall Glacier, additional open symbols mark locations optically surveyed in 1972 and 1993. The acquisition dates for map photography and GPS profiles are given for each glacier fallowing the abbreviations “m” and “p”, respectively. Roman numerals indicate the corresponding topographic map in Table 3. Dotted curves represent the new terminus outlines calculated by our volume-change algorithm. Surveyed terminus outlines for different years are shown for W. Okpilak Glacier and McCall Glacier.
We also distinguish between net accumulation, which is the net amount of annual precipitation and possibly refrozen melt that is added to the glacier, and winter balance, which is the maximum snow balance on top of the last summer surface in the spring.
All mass balances are given in water equivalent unless otherwise noted and all balances, including long-term averages calculated over several decades, are given as annual values.
Mass-Balance record Of Mccall Glacier
The mass-balance record on McCall Glacier is fragmented. A few ablation measurements were made in the mid 1950s (Reference KeelerKeeler, 1958), a new program was initialed in 1969 and continued until 1972 (Reference Trabant and BensonTrabant and Benson, 1986; Reference Wendler, Fahl and CorbinWendler and others, 1972) and our ongoing program began in 1993. These monitoring programs generally involved annual balance measurements using the Glaciological method. In addition, average balances over longer periods were determined using the topographic method, as described by Reference Dorrer and WendlerDorrer and Wendler (1976) and Reference Rabus, Echelmeyer, Trabant and BensonRabus and others (1995). In this section, we present the results of these programs in an internally consistent framework. Because the measurement techniques and methods used to calculate annual balance differed, we first describe the methods by which the basic data were obtained and then describe a re-evaluation of the earlier data within our present framework, along with an analysis of the errors. We are then able to discuss changes in mass balance, focusing on the differences between the 1970s and the 1990s. No annual mass-balance measurements are available from the 1950s.
Glaciological mass-balance methods: 1970s
In 1969, Reference Trabant and BensonTrabant and Benson (1986) established a network of about 70 mass-balance poles. The heights of the poles were measured monthly from May to September, and snow-pit measurements were made in spring and fall. A fixed hydro-logical year, beginning 1 October, was used. Glacier-wide net balance was determined, along with the individual components of ice, superimposed ice, internal accumulation and snow. However, the exact computational method used in calculating glacier-wide balances from local balances is not known but most likely the balance-map method was used. They estimated the error in the net balance to be ± 5 cm for the 1970, 1971 and 1972 balances and ± 8 cm for the 1969 balance.
In-situ measurements of internal accumulation were carried out by Trabant and Benson. They monitored the growth of individual ice layers in the firn at specific-locations. However, the spatial pattern of internal accumulation was irregular and it was felt that extrapolation to unmeasured areas would be inaccurate. Instead, an indirect method was used. Potential internal accumulation was restricted to areas where the glacier surface was judged to be permeable to water, both meltwater and rainfall. For each pole in this permeable area, a maximum capacity for internal accumulation was calculated using shallow-ice temperatures. The average capacity was about 45 cm per unit area (water equivalent), with only small spatial and year-to-year variations. The available surface water was calculated from measured summer precipitation plus the difference between the spring snow balance and the autumn firn balance. Internal accumulation was then taken to be the smaller of the available water and the maximum capacity. An important result of this analysis was that the capacity for internal accumulation was usually much larger than the available water (Reference Trabant and BensonTrabant and Benson, 1986). Therefore, internal accumulation on Arctic glaciers is probably “liquid limited” vs “thermally limited”. It was also found that up to 40% of the net accumulation on the glacier was in the form of internal accumulation, making it a significant contribution to the mass balance of this Arctic glacier.
Glaciological mass-balance methods: 1990s
Our mass-balance measurements cover the period 1993–96. A network of 16 poles along the center line of the glacier and in the three cirques was established in mid-June 1993. It was extended to 34 poles in 1995 in an effort to establish an areal coverage similar to that in the 1970s. For each of the (our years, the pole heights were measured early in the spring (May to mid-June) and near the end of the ablation season (July – early September). Density profiles of the snowpack were measured in spring and autumn at one–three locations. No autumn density measurements were made in 1994 or 1996.
Contrary to the 1970s, we used the stratigraphie system to define the balance year in the 1990s. Late-summer surfaces at each pole were determined by probing through the winter snow each spring. With the exception of an area in the upper cirque in 1994, identification of the summer surface was usually unambiguous. Snow balance was measured at each pole and at some additional sites, giving a total of 24–54 locations each year where we determined winter balance.
For the years 1995 and 1996, we established correlations between the local balance measured at the poles within the limited 1993 network (with 16 poles) and that at the additional poles of the extended network. We then used these correlations to extend the limited measurements in 1993 and 1994 to a greater areal coverage in those years. Balance maps were constructed from each year’s data, using this extrapolated coverage as needed. All balances for 1993–96 were calculated using this method, sampling the map on a 100 × 100 m grid.
A sonic snow-surface sounder was installed at the confluence of the three cirques, somewhat below the mean 1970s equilibrium line, for measuring accumulation and ablation. Continuous records exist for June 1993 – June 1994, and for May–September 1996. These records show that, typically, the ablation season began in the first week of June and ended in mid-August, thus being less than ![]() months in duration. The maximum snow depth at this location was about 60 cm; this snow and between 25 and 50 cm of ice were melted during the ablation season. Most of the snowfall occured in late August, September and May; there was little winter precipitation.
months in duration. The maximum snow depth at this location was about 60 cm; this snow and between 25 and 50 cm of ice were melted during the ablation season. Most of the snowfall occured in late August, September and May; there was little winter precipitation.
Internal accumulation was estimated following a procedure similar to that used in the 1970s. The total available water percolating into the permeable zone was approximated by the spring snow balance minus the autumn firn balance, plus summer precipitation. Rainfall was measured at a precipitation gauge located on the eastern moraine at an elevation of 2100 m. The extent of the permeable zone was delineated from field observations. This provided a relatively crude but consistent estimate of internal accumulation. We discuss this important contribution below.
How do we obtain an error estimate for the balance-map approach Reference LliboutryLliboutry (1974) modeled the mass balance of an individual pole as the sum of three terms: a spatial term, a temporal term and a random error of about ± 20 cm. This error incorporates (i) the individual reading error, typically-largest in the accumulation area, (ii) the mismatch between the individual pole and the local average, and (iii) extrapolation errors of limited pole networks. Reference Cogley, Adams, Ecclestone, Jung-Rothenhäusler and OmmanneyCogley and others (1996) claimed that the error of the glacier-wide balance equals Lliboutry’s value for an individual pole. We take a different view point: if the network has sufficient areal coverage, then the error is dominated by the components (i) and (ii). As these errors should be randomly distributed among the poles, the average glacier-wide error should be reduced according to ![]() , where n is the number of poles in the network. For example, with 30 poles, we obtain a value of ± 4 cm for an estimate of the random error in annual balance. Insufficient areal representation of the mass-balance network and systematic errors in the extrapolation of snow and firn density will somewhat increase this value. Given these and other sources of error, we arrive at ± 8 cm as a conservative error estimate for the annual balances. It applies only to the surface balance, without internal accumulation. Errors in the internal accumulation cannot be analyzed rigorously with the measurements in hand; below we present minimum and maximum scenarios for this contribution.
, where n is the number of poles in the network. For example, with 30 poles, we obtain a value of ± 4 cm for an estimate of the random error in annual balance. Insufficient areal representation of the mass-balance network and systematic errors in the extrapolation of snow and firn density will somewhat increase this value. Given these and other sources of error, we arrive at ± 8 cm as a conservative error estimate for the annual balances. It applies only to the surface balance, without internal accumulation. Errors in the internal accumulation cannot be analyzed rigorously with the measurements in hand; below we present minimum and maximum scenarios for this contribution.
Re-evaluation of the 1970s balance data
In order to ascertain the specific methods utilized with the earlier dataset, and to place all the mass-balance calculations into a consistent framework, we have re-evaluated the Glaciological mass-balance data from the 1970s (unpublished information from D. Trabant) under the protocol just described for our 1990s data. First, we calculated the balances using a fixed-date system in order to check our values with those published by Reference Trabant and BensonTrabant and Benson (1986). These calculations were carried out on the entire dataset of about 70 poles and on a sub-set of the network that was equivalent to the 34 poles measured in 1995–96. We re-evaluated the net balance on these two networks using two approaches (table 1): balance maps b map and the balance vs elevation method (b elev) with a third-order polynomial fit to the balance curve and an area–elevation curve derived from the 1956 USGS 1:63 360 map. Net accumulation, α map, derived from the balance maps, is also given in the table. In the last section of Table 1 are listed the published values of these parameters from Reference Trabant and BensonTrabant and Benson (1986), along with their value of internal accumulation, α (i).
Table 1. Re-evaluation of 1970s mass-balance data (fixed-date system). Units in cm

There are several points to notice from this table. First, the values that we calculated using only data from the 1995–96 sub-set agree with those from the full network to within ± 5 cm. This suggests that the sub-set provides adequate area! coverage. Secondly, b map generally agrees with b elev to within one standard error (± 8 cm), an encouraging result given the complex shape of the mass-balance contours on these maps (Fig. 3). Thirdly, the agreement between the recalculated values and those listed by Reference Trabant and BensonTrabant and Benson (1986) is within the standard error but, because we used the same data, it is somewhat surprising that the agreement is not better. These differences do imply that a re-evaluation under our framework is necessary for developing an internally consistent analysis of the mass-balance record.
To facilitate this, we treated the 1970s data in exactly the same way as those of the 1990s. We first transformed the individual pole balances from the fixed-date system into the stratigraphie system, subtracting the difference of the initial and final snow balances for the balance year. We then used the balances for those poles in the 1995–96 sub-network to construct balance maps for the years 1969–72.
Results for the combined mass-balance record 1970s and 1990s
The combined mass-balance record for the periods 1969–72 and 1993–96 in the stratigraphie system is given in Table 2. The first two data columns show the surface balance b (s) and its corresponding accumulation area ratio (AAR). The following columns show net balance b, net accumulation a, internal accumulation α (i), and the net balance AAR and ELA. For the 1990s, the net values are given for minimum and maximum calculations of internal accumulation, which are discussed below. b w and p s are quantities needed for these calculations; b w denotes the maximum winter balance, which we approximate by the snow balance on the date listed, and p s is the summer precipitation measured at our precipitation gauge between the date listed and 10 August, the last day of significant melt. The ELA is an average elevation for the equilibrium line; the actual line of zero balance often spans about 300 m in elevation, as already noted.
The 4 year average annual surface balance was –29 ± 3 cm from 1969 to 1972 and –63 ± 3 cm from 1993 to 1996, indicating a pronounced trend towards more negative surface balances from the 1970s to the 1990s. This trend is apparent despite the inclusion of the exceptionally cold year 1996, which had the most positive balance ever measured on McCall Glacier. The balance maps for the surface balances 1969–72 and 1993–96 are shown in figures 3 and 4, respectively. In the 1970s, the lower (western) cirque was always an area of accumulation and maximum ablation near the terminus was always less than 180 cm a−1. In contrast, the years 1993–95 were characterized by considerable ablation of old firn and ice in the lower cirque and a maximum ablation of more than 200 cm a−1 near the terminus. In 1994, the year with the most negative surface balance, maximum ablation exceeded 350 cm. For these 3 years, firn accumulation was restricted to two small regions in the centers of the upper and middle cirques. In contrast, 1996 was more similar to the 1970s regarding the patterns of firn accumulation and ablation. Examination of the balance maps (figs 3 and 4) confirms that there is no meaningful definition of a specific ELA on McCall Glacier.
From a climatological point of view, it is the surface balance of an Arctic glacier that corresponds to the usual mass balance of warmer temperate glaciers, which is given as the simple difference between summer ablation and winter accumulation. The net balance of an Arctic glacier additionally includes internal accumulation and therefore also depends on other factors, such as mean winter temperature, the permeability of the glacier surface to water and rainfall on the snowpack. We require both surface and net balances to calibrate the mass-balance model presented in a later section, and thus we need an accurate estimate of internal accumulation in the 1990s.
Scenarios of internal accumulation
Because internal accumulation is difficult to measure directly (Reference Trabant and MayoTrabant and Mayo, 1985), we estimate it. Near-surface firn temperatures in the 1990s were similar to those in the 1970s, and thus the capacity for internal accumulation should be approximately equal to its mean value determined in the 1970s (Reference Trabant and BensonTrabant and Benson, 1986). We then propose two possible scenarios for the extent of the glacier surface where internal accumulation may occur (the “permeable zone”): (1) an area equal to the region of positive firn balance in a given year, and (2) an area equal to the permeable zone in the 1970s. Scenario 1 provides a minimum estimate of internal accumulation, while 2 provides a maximum estimate for the 1990s. We begin with a discussion of these different assumptions.
Table 2. Combined record of annual surface and net mass balancer (stratigraphie system)


Fig. 3. Balance maps of the stratigraphie surface mass balance, 1969–72. Contours of equal mass balance are shown for –200, –100, –50, 0, +25 and +50 cm water equivalent. The 0 cm contour is the equilibrium line (E.L.). Glacier-wide annual balances are noted.

Fig. 4. Balance maps of the stratigraphie surface mass balance, 1993–96 (contour labels as in Figure 3). Glacier-wide balances are noted. The asterisk shows the location of the sonic ranger.
In the 1970s, the area assumed to be permeable was approximately equal to the area of fini accumulation (i.e. where the local surface balance was positive). For the years 1993–95. accumulation of new lira was negligible, with surface-balance AARs as small as 0.02. Under these conditions, scenario (1) leads to very small amounts of internal accumulation (Table 2, column 6).
Scenario (2) involves considerable internal accumulation outside the area of new firn accumulation in the 1990s and, as such, is a maximum estimate. It is important to note that internal accumulât ion need not be restricted to areas of the surface that are porous in a microscopic sense. For example, Reference SaterSater (1959) noticed dial a large number of small crevasses (5–20 cm wide) opened in the upper ablation area during the cold winter months, but they were closed by re-freezing of water in summer. This process acts as a sink for internal accumulation in the early melt season. It also makes the surface impermeable to water in the late melt season. We note that for years 1993–95 internal accumulation exceeds net accumulation under this scenario (Table 2, columns 11 and 10). This is a direct result of the large amount of old firn that is ablated and becomes run-off in the late melt season, along with some melt of the early season internal accumulation. For 1996, maximum and minimum scenarios of internal accumulation are similar, with internal accumulation being about 25% of the net accumulation. This is similar to that observed in the 1970s mainly because the permeable zone actually had about the same extent during these time periods.
The large contribution of internal accumulation to the mass balance of Arctic glaciers such as McCall Glacier is significant because estimates of water released by these glaciers to sea-level rise may need to be re-evaluated if based solely on surface-balance measurements. This has been discussed by Pfeffer and others (1990) in application to the Greenland ice shed.
Topographic mass-balance measurements
Cumulative net mass balances for the time intervals between the field programs can be determined using glacier surface-elevation data obtained by photogrammetry or surveying; these cumulative balances can then be divided by i be number of years in the intervening time to give the average net balance over each interval. Comparison of these long-term topographic balances with the net balances presented above then gives a picture of mass-balance trends during the last 40 years. The long-term average balances also provide useful constraints on the mass-balance modeling described in a later section.
A direct photogrammetric comparison by Reference Dorrer and WendlerDorrer and Wendler (1976) gave a value of –13 cm for the long-term average annual balance from 1958 to 1971, a somewhat less negative value than the average of the 1970s net balances (–19 cm). In another study, Reference Rabus, Echelmeyer, Trabant and BensonRabus and others (1995) compared the elevations at about 60 locations on the glacier surface, as surveyed in 1972 personal communication from D. Trabant), with a 1958 topographic map (American Geographical Society 1960). However, there are large systematic errors in the 1958 topographic map and, thus, it was difficult to make a reliable estimate for the 1958–72 mass balance using this method. While we cannot directly evaluate the errors in Reference DorrerDorrer’s (1975) analysis (that method did not involve the 1958 map), we believe them to be smaller than those associated with the 1958 map. As an independent check, we have also compared the above-mentioned 1972 vertical elevations with a 1:63 360 scale topographic map produced by the U.S. Geological Survey (USGS) from 1956 photography. Despite the larger error inherent in the coarser contour interval (100 ft or 30.5 m), this comparison gave an estimate of –17 ± 6 cm for the long-term average balance from 1956 to 1972. This value is close to that of Reference Dorrer and WendlerDorrer and Wendler (1976) and, combining the two estimates, we obtain a value of –15 ± 5 cm for the 1958–72 average annual net balance.
By resurveying the 1993 surface elevation at the same positions used in 1972, Reference Rabus, Echelmeyer, Trabant and BensonRabus and others (1995) determined the average annual net mass balance for the period 1972–93 to be –33 ± 1 cm. This is significantly more negative than the 1958–72 average balance of –15 ± 5 cm, thus giving further support to a change in climate in this region.
In June 1995, the surface elevations at about 40 of these positions were again resurveyed. Combination of these data with snow depths at each site allowed us to calculate the volume change, and thus make a topographic estimate of the average mass balance for 1993 and 1994. Using a density of 0.90 Mg m−3 to convert ice to water equivalent, an annual value of –65 ± 6 cm was obtained for these 2 years. (This value of density may introduce a slight bias toward a more negative balance because there was significant ablation of old firn during both years (Reference KrimmelKrimmel, 1989).)
We can compare this average 1993–94 balance with those presented in Table 2 under the different scenarios of internal accumulation. Taking the average of the 1993 and 1994 balances in this table, we find ![]() , and
, and ![]() for the 1993–94 period. The close agreement between the latter value and the topographical value (–65 ± 7 cm) implies that the scenario that predicts maximum internal accumulation is probably more realistic. Comparison of the Glaciological surface balance and topographical balance yields a value of 22 cm for the mean annual internal accumulai ion over this 2 year period. These results suggest that the zone of permeability, where internal accumulation occurs, is much larger than the area of firn formation during warm summers. This further suggests that alternative processes of internal accumulation, such as refreezing of water in crevasses, may be important.
for the 1993–94 period. The close agreement between the latter value and the topographical value (–65 ± 7 cm) implies that the scenario that predicts maximum internal accumulation is probably more realistic. Comparison of the Glaciological surface balance and topographical balance yields a value of 22 cm for the mean annual internal accumulai ion over this 2 year period. These results suggest that the zone of permeability, where internal accumulation occurs, is much larger than the area of firn formation during warm summers. This further suggests that alternative processes of internal accumulation, such as refreezing of water in crevasses, may be important.
In a similar study, Haakensen (1986) has found that long-term topographic balances and cumulative surface balance on an Arctic glacier in Norway differ by about 14 cm, while these two types of balance agree quite well for the more temperate glaciers he studied. Haakensen interpreted these differences as internal accumulation of an amount equal to 14 cm a−1.
Record of net mass balance and possible implications
In Figure 5 we compile the valions net balances discussed above. The maximum scenario of internal accumulation was used for the 1990s (right side of Table 2). A strong trend toward increasingly negative mass balances stands out clearly, with high inter-annual variability about this trend. An even more negative trend would be shown if the minimum scenario for internal accumulation were used.
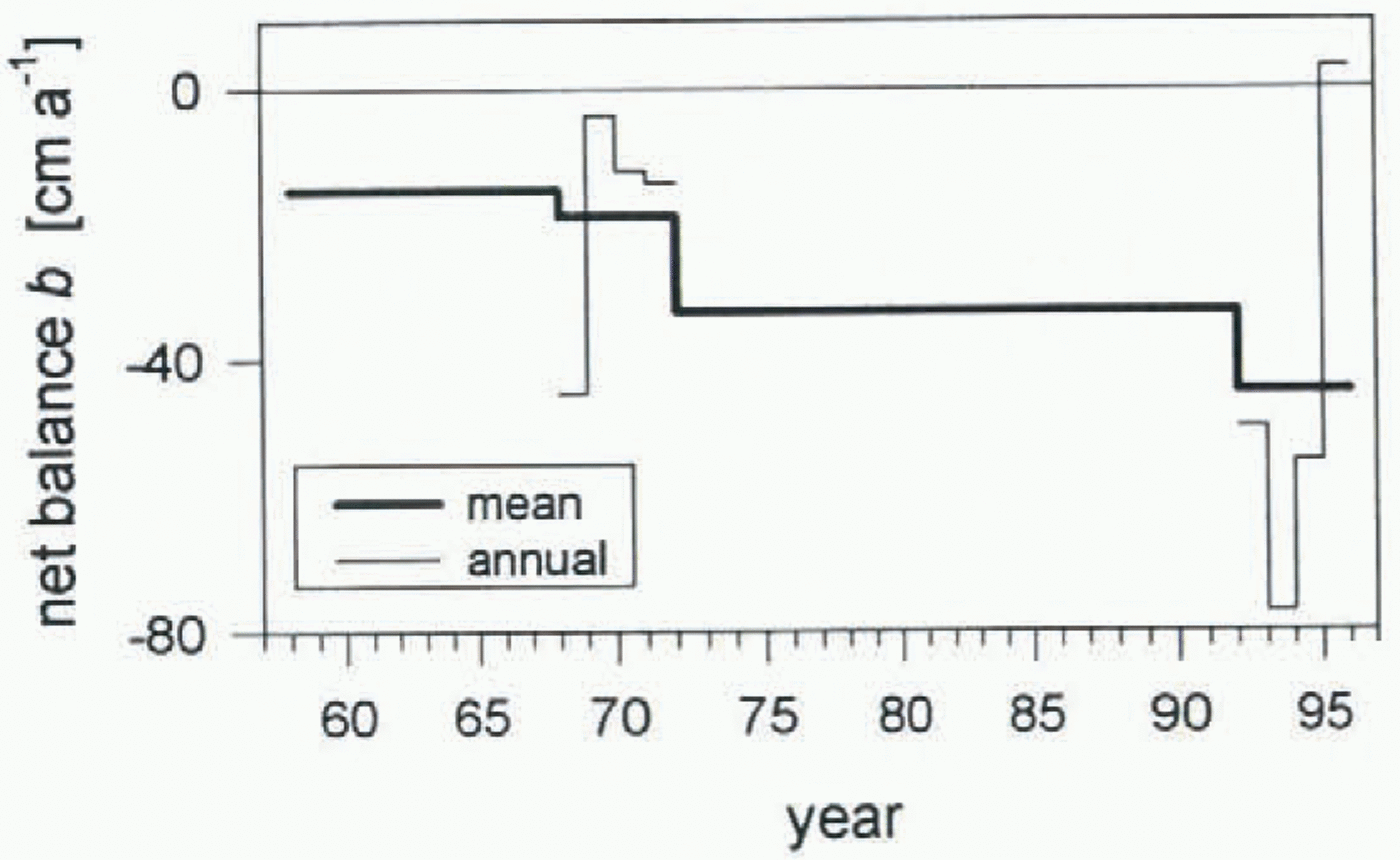
Fig. 5. Net mass-balance record of McCall Glacier. The record is combined from the topographically determined long-term average values, 1957–72 and 1972–93, and the average balances during the 4 year periods 1969–72 and 1993–96 (bold line). The individual annual net balances are also shown (thin line).
By applying an approximate mass-balance model to a variety of glacierized regions, Reference OerlemansOerlemans and Fortuin (1992) found an empirical relation, Δb (1K) = –0.512 – 0.662 log10 (P), between the mean annual precipitation, P (about 0.5 m a−1 on McCall Glacier), and the mass-balance response Δb (1k) of a glacier to a uniform 1 K increase in mean annual temperature. If we assume that the observed changes in average net balance, Δb, on McCall Glacier are caused by a uniform change in temperature, and that the precipitation is nearly constant, then we can use Oerlemans and Fortuin’s model to estimate the causal temperature change as ΔT = 1K × (Δb/Δb (1K)). From 1957–72 to 1972–93, we find an estimated increase of 0.6 K in air temperature for this 20+ year interval. (Similarly, we would obtain an additional 0.4 K temperature increase from 1972–93 to 1993–96; however, the short duration of the later period makes this estimate unreliable). Of course, the precipitation need not be constant over these intervals.
Mass-balance gradient
The gradient of local surface balance with elevation reflects the climatic regime of a glacier. A long-term change in the balance gradient may indicate a change in the climate towards one which is more continental or more maritime (e.g. Reference Oerlemans and HoogendoornOerlemans and Hoogendorn, 1989). To investigate this possibility, the annual surface balance as a function of elevation was calculated from the balance maps in figures 3 and 4. For each of the two time periods we used the concurrent surface elevation, thus taking into account the significant thinning since the 1970s. The results are shown in Figure 6. Since the 1970s there has been an increase in the variability of the local mass balance. Linear regression of the mass-balance curves as a function of (concurrent) elevation for the 1970s and for the 1990s gives the heavy lines shown in these figures. The average annual balance gradient for the 1970s was 172 ± 4 cm km−1 and 201 ± 6 cm km−1 for the 1990s. Without the exceptionally cold year in 1996, the balance gradient in the 1990s would be slightly higher (210 cm km−1). We conclude that there has been a significant increase in the balance gradient on McCall Glacier from the 1970s to the 1990s. A possible interpretation is a larger mass exchange in the 1990s, with the more negative balances being caused by a disproportionate increase of ablation at lower elevations. The mass-balance modeling described in a later section lends further support to such a change.
Regional Representivity of Mccall Glacier Mass Balance
The data from McCall Glacier comprise the only long-term record in Arctic Alaska. One may question how representative this record is in a regional context. To investigate whether the trends in the McCall Glacier balance reflect a coherent regional signal, we measured changes in surface elevation along the center lines of ten other glaciers in the northeastern Brooks Range (Fig. 1). Our surveys were carried out once on each glacier during the period 1993–95, and the elevation changes with respect to 1956 or 1973 topographic maps were used to estimate long-term mass balances over the intervening time period.

Fig. 6. Surface mass balance bs as a function of elevation z: (a) for the period1969–72, and (b) for the period 1993–96. For both periods, z is the actual surface elevation at that time. In each case, the heavy line represents a linear least squares fit of all four mass-balance curves bs (z).
The surveyed glaciers fall into three morphological groups (Fig. 2): larger valley glaciers (McCall, Esetuk and the two Okpilak Glaciers), smaller valley glaciers (Arey, Wolverine Crag, Gooseneck, Bravo and the two Hubley Glaciers,) and one cirque glacier (Hanging Glacier). The distance from McCall Glacier to Arey Glacier is about 5 km, and about 20 km to Esetuk and the two Okpilak Glaciers. All the other glaciers are immediate neighbors of McCall Glacier, that is, their drainage basins are within or have a common border with the McCall Glacier drainage basin.
Topographic maps
Four adjacent USGS maps of scale 1:63 360 and a contour interval of 100 ft (30.5 m) were used in this analysis. The datum of the maps is NAD27, with elevation given above mean sea level. Mapping photography was acquired in two different years: 1956 and 1973. The maps for each glacier, numbered I to IV, and the dates of photography are given in tables 3 and 4.
Three significant error sources can be present in the elevation contours of these maps (Reference EchelmeyerEchelmeyer and others. 1996): (i) a random error on the order of ± 15 m, (ii) local systematic errors in regions where the photographs have poor stereoscopic quality, and (iii) a systematic offset between the map and the true elevation. The latter errors can be on the order of 20 m because geodetic control for the photogrammetry was extremely sparse in this part of North America.
Table 3. Measured elevation offsets for the topographic map sheets of this study

The random error will cause fluctuations about a smooth curve of elevation change vs elevation on a glacier, but its effect on the cumulative mass balance (as an area-weighted average of elevation change) is reduced by the square root of the number of contours considered (Reference EchelmeyerEchelmeyer and others, 1996).
Potential systematic offsets for each map were identified in two ways: either we surveyed the true elevation of topographic highs that were labeled to ± 10 ft (3 m) on the maps (“spot elevations”) using static Global Positioning System (GPS) methods, or we made airborne laser/GPS profiles (Reference EchelmeyerEchelmeyer and others, 1996) over bedrock surfaces and evaluated the elevation difference between the profiled bedrock and the map contours. A geoid model (Alaska 94) was used to relate these ellipsoid heights to mean sea level. Mean vertical deviations, ![]() , between our surveys and the map elevations are given in Table 3 for both the spot elevations and the bedrock profiles. The corresponding standard deviation, σ, and the number of surveyed points, n, are also shown. The GPS elevations have an accuracy of 0.5 m or better.
, between our surveys and the map elevations are given in Table 3 for both the spot elevations and the bedrock profiles. The corresponding standard deviation, σ, and the number of surveyed points, n, are also shown. The GPS elevations have an accuracy of 0.5 m or better.
No significant vertical offset was found for map I. Both spot elevations and profile data show that map II is consistently 20 ± 2 m higher than the measured elevations. The situation on map III is somewhat more complex. A spot measurement made a few kilometers south of West Okpilak Glacier shows the map is 17 m higher than the measured value, while profile measurements made about 10 km north of the glacier indicate that the map is 14 m lower than expected. In the immediate vicinity of the glacier terminus we find that the map is 2 ± 3 m lower than the profiled surface. The interpretation of this pattern as a ramp-like north-south offset clearly needs more survey data. In lieu of such data, we assume a zero constant offset (Δz ≈ 0 m) for this map in the vicinity of West Okpilak Glacier. Map IV was not field-checked and we used Δz ≈ 0 m from the adjoining map (III). These choices assure similar small elevation changes in the upper accumulation areas of both West and East Okpilak Glaciers. The mean offsets for each map were used to correct map contour elevations.
Table 4. Mass-balance and terminus changes, 1956 or 1973 to present, of 11 Brooks Range glaciers

Local systematic errors can be identified by unreasonable deviations in the elevation-change curves of the different glaciers. Also, we have examined the actual mapping photographs for areas of poor contrast. In most cases, these local errors appear to be relatively small. However, their effect on the cumulative balance depends crucially on the area distribution of a particular glacier, as errors in extensive accumulation areas can strongly influence such mass-balance calculations.
Survey methods
Three different GPS-based methods were used to survey the center-line elevations and termini of the glaciers. In 1993, an airborne profiling system was used (Reference EchelmeyerEchelmeyer and others, 1996). The horizontal and vertical accuracies of this system are about ± 0.3 m. In 1994 and 1995, we used two different ground-based methods. The more accurate (±0.3 m) involved continuous kinematic GPS profiling while skiing down the glacier. The second method utilized a lightweight differential GPS system to determine the coordinates of specific points along a center-line profile relative to a nearby benchmark. The vertical accuracy of this latter method was ± 3 to ± 8 m, depending on conditions.
Elevation and volume change
The ground tracks of the profiles on each glacier are shown in Figure 2, superimposed on topographic maps. Profiles of Arey and Wolverine Crag Glaciers consist of isolated survey points acquired with the less accurate ground-based method discussed above. On the other glaciers, the profiles were acquired with either the airborne or the high-accuracy ground-based methods, with points spaced every 1–1.5 m along the profile.
Horizontal coordinates of each GPS profile were transformed from the WGS84 datum to the map datum (NAD27). Vertical height above the ellipsoid was transformed to elevation above mean sea level using the Alaskan geoid model. The geoid separation above the ellipsoid in our study area varies between +3 and +6 m.
Elevation change was obtained by determining the elevation at each point where the profile intersected a map contour line. Cubic-spline interpolation was used between the data points on Wolverine Crag and Arey Glaciers. The random error of elevation change is dominated entirely by the ±15 m random error in the map contours. Even in the case of the less accurate GPS method, the combined error is only slightly larger, ±17 m.
To determine the change in glacier volume using a single longitudinal profile on each glacier, we assumed that the elevation change at each contour was constant across the width of the glacier. As the glacier thinned or thickened, its width, and therefore area, would also change. We estimated this change in width by multiplying the elevation change along a specific contour line by the cotangent of the slope of the valley walls at that contour. The projected 1990s outlines of each glacier, as determined using this algorithm, are shown in Figure 2 as dotted lines. The terminus outlines of McCall and West Okpilak Glaciers were also surveyed to a horizontal accuracy of ±2 m using GPS methods. There was satisfactory agreement between these surveyed glacier outlines and those calculated by our algorithm.
Volume change was then calculated following the method of Finsterwalder (1954). The area-averaged thickness change was obtained by dividing the total change in volume by the area of the glacier, here taken to be the average of the mapped area and the 1990s area. The average net mass balance (water equivalent) was calculated by dividing by the time interval and assuming a density of 0.90 Mg m−3, thus taking the density distribution with depth to be constant.
A rigorous error estimate for the volume-change calculation involving a single center-line profile is difficult to obtain (e.g. Sapiano and others, 1998). We estimated this error from the following analysis of the McCall Glacier data: elevation changes along two center-line profiles, one descending from the upper cirque and the other from the lower cirque, were determined using the optical survey data from 1972 and 1993 (open symbols on the McCall Glacier map in Figure 2). These elevation changes were then used to calculate the cumulative balance from 1972 to 1993, and the results were compared to those from a two-dimensional interpolation of the entire set of surveyed positions, including all those off the center line (Reference Rabus, Echelmeyer, Trabant and BensonRabus and others, 1995). The profiles yielded an average change of –7.6 m of water, which agrees within 10% of the value –6.9 m quoted by Reference Rabus, Echelmeyer, Trabant and BensonRabus and others (1995). A similar error estimate on another glacier was obtained by Reference Sapiano, Harrison and EchelmeyerSapiano and others (1998) using a different method.
The contribution of local systematic errors was investigated by comparing the volume change for a smoothed elevation-change curve with that for the original unsmoothed curve. In most cases, the difference in volume change was less than 10%. In the case of West Okpilak Glacier, where the difference was greater than 10%, we used the smooth version of the curve.
Results
Elevation changes on these different glaciers are shown as a function of 1990s elevation in figures 7 and 8 for the two periods 1956–93 and 1973–93, respectively. In both figures the plot in the upper lefthand corner shows the average elevation change for all the glaciers in the time period considered (solid line), along with one standard deviation about this average (light gray) and the envelope of all values of elevation change for the glaciers (dark gray). This plot is useful in determining how meaningful the average elevation change is. All glaciers show strong thinning at lower elevations and a decrease in the magnitude of this thinning with increasing elevation. For 1956 to the 1990s, the average elevation change was about –60 m at 1400 m and about –14 m at 2000 m; they were about 15 m smaller for the period from 1973 to the 1990s.
For all other plots in figures 7 and 8, the elevation change on the individual glaciers is compared to the average elevation change for all glaciers over the same time period. For the period 1956–93 (Fig. 7), the elevation changes of Esetuk, Gooseneck, Bravo and South Hubley Glaciers agree well with those on McCall Glacier. North Hubley and Wolverine Crag Glaciers show significantly larger elevation changes than those observed on McCall Glacier. During the 1973–93 period (Fig. 8), elevation changes on West and East Okpilak and Arey Glaciers were similar to those on McCall Glacier. Table 4 contains further results on the different glaciers. The first part of this table shows the dates of survey and the methods used, and geometric parameters of the glaciers, including mean glacier area A, glacier length L, elevation of the terminus (z min) and head of the glacier (z max), all al the time of mapping; and the mean aspect of the glacier. The second part of the table gives the volume change, ΔV, the area-averaged elevation change for the time period, Δz (A), the long-term average net balance, and the change in terminus position, ΔL, from the date of mapping to the 1990s. In order to assess the representivity of McCall Glacier, we have also calculated the ratio of the mass balance of the study glaciers to that for McCall Glacier (second to last column of Table 4). Values range from 0.04 to 1.9. However, the majority of glaciers had values of 1.0 ± 0.2, that is, their average mass balances are within 20% of the McCall Glacier balance. Four of the glaciers have somewhat more negative balances of around –50 cm, while the smaller cirque glacier (Hanging Glacier) was close to equilibrium.

Fig. 7. Elevation change (in m) between 1956 topographic maps and recently surveyed center-line profiles of McCall Glacier and seven neighboring glaciers as a function of elevation (in m). The upper left panel shows the mean elevation change for all glaciers (solid line), one standard deviation (light gray) and the maximum spread of elevation change (dark gray) about this mean. The other panels compare the individual elevation changes (heavy curve and symbols) with the mean for all glaciers (thin line). The survey method and acquisition date of the individual profiles is indicated., with abbreviations “airb” “gr.b.1” “gr.b.2” for airborne, high-accuracy ground-based and low-accuracy ground based GPS methods, respectively.

Fig. 8. Elevation change (in m) between 1973 topographic maps and recently surveyed center-line profiles of McCall Glacier and three neighboring glaciers as a function of elevation (in m). Explanations are the same as in Figure 7. The additional abbreviation “opt.” stands for optical surveying, which was used in 1972 and 1993 to calculate the elevation change on McCall Glacier.
The observed variations in mass balance between “anomalous” and “normal” glaciers could reflect corresponding differences in geographic location, area–altitude distribution, aspect or size (e.g. Tangborn and others, 1990). However, for the northeast Brooks Range glaciers, we found no indication of any simple relationship between mass-balance variations and any of these factors.
In summary, the data from the various glaciers indicate that the mass-balance trends of McCall Glacier are representative for the region of the northeastern Brooks Range. Most of the glaciers studied show an overall thinning al the rate of 30–40 cm a−1 (ice). Pelto (1996) has reported a similar uniformity in the annual mass balance for eight glaciers in the North Cascades. The average balance of these temperate glaciers was –39 cm over a 10 year period (1984–94), and there was a strong correlation between time series of annual balance for the different glaciers. The regional average and glacier-to-glacier variations in mass balance observed by Pelto were similar in magnitude to those we found in the northeast Brooks Range and, because of this, we might expect a similar degree of correlation between mass-balance trends of different glaciers in this part of the Brooks Range. Thus, the mass-balance trends that we have found on McCall Glacier may well represent regional trends.
Mass balance and changes in terminus position
While the long-term mass balances of our different study glaciers are for the most part similar, the corresponding rates of terminus retreat are not. In Figure 9, we show the relative change in length of each glacier. There is no consistent picture, except that each glacier has retreated. For instance, compare McCall Glacier with Gooseneck and East Okpilak Glaciers. The elevation-change curves and the average mass balances over the respective time periods are nearly identical (Table 4; Figs 7 and 8), yet over the same time periods McCall Glacier retreated substantially, while Gooseneck Glacier showed negligible retreat and East Okpilak Glacier showed four times more retreat than McCall Glacier (Fig. 9). This is probably due to the particular geometry of each glacier, especially that near the terminus (e.g. Gooseneck Glacier had a vertical terminal ice face in 1956 that thinned without retreat to produce the gentle ice slope existing at present). It is clear from the results of this section that retreat of the termini of different glaciers is a complex function of glacier geometry and mass balance, a finding similar to that of Reference EchelmeyerEchelmeyer and others (1996) and Reference Sapiano, Harrison and EchelmeyerSapiano and others (1998) for different locations. Lichenometric dating of late Holocene moraines by Calkin and Evison (1996) also indicates a complicated pattern of terminus changes since the end of the Little Ice Age (about AD 1890) in this region of the Brooks Range.
The Mass Balance of Mccall Glacier and Climatic Change in the Arctic
In this section we investigate the correlation between the mass balance of McCall Glacier and climatological data from weather stations 100–650 km away from the glacier. These correlations are used to determine how representative the balance of McCall Glacier is for this part of the Arctic on a larger (“synoptic”) scale. We utilize an empirical degree-day model for the mass balance, with the mass-balance data from the 1970s and 1990s and a combination of daily and monthly weather-station data. Using this model to fill gaps in balance record then allows us to speculate on the climatic causes of the increasing negative balance trend and glacier thinning.
The locations of the weather stations considered in this study are shown in Figure 1 (inset) and relevant parameters are given in Table 5. We focus on the summer temperatures at these stations, which are possibly related to ablation, and precipitation during the months in which accumulation on the glacier is likely.
Model description
Physical mass-balance models use meteorological input data to predict the energy and mass fluxes at the surface of a glacier, from which the mass balance is derived. These models require high-resolution energy-balance measurements and have generally been developed for temperate glaciers (e.g. Reference OerlemansOerlemans, 1992; Reference Conway, Rasmussen and HayesConway and others, 1995), and they do not account for internal accumulation. For these reasons, we use an empirical mass-balance model, essentially a least-squares regression of the measured mass-balance series with two climatological inputs. The first is the sum of positive degree days, D, as calculated from twice-daily radiosonde soundings made at one of the weather stations listed in Table 5. D is calculated for the median elevation of the glacier, about 2000 m. The second input is accumulation, A, as calculated from precipitation measured at one of the stations. The balance model is then simply the linear combination
where Δ marks per-cent deviations of quantities from their corresponding means during the calibration period. (If, instead, b is modeled as a function of D and A, rather than of their deviations (Δ), then a third constant appears on the righthand side. This constant can be expressed as a function of the mean values of b, A and D.) The constants c d and c a are determined by the least-squares fit of Equation (1) to the set of eight measured mass balances given in Table 2. Models for both the surface and the net balances (maximum internal accumulation) are presented.

Fig. 9. Regional patterns of changes in glacier length (relative to length) for northeast Brooks Range glaciers from 1956 to the 1990s and 1973 to the 1990s.
Table 5. First-order weather stations within 700 km radius of McCall Glacier

Specification of the actual input parameters requires some care. Surface temperature is often influenced by local effects, such as selective heating and low stratus clouds, especially in Arctic coastal locations. For this reason, we follow Sampson (1965) and Reference Conway, Rasmussen and HayesConway and others (1995) in using the air temperature over a weather station at the median elevation of McCall Glacier, which generally falls between the 850 and the 700 mbar pressure levels. We have found that the mean layer temperature,

shows a better correlation with measured temperatures on the glacier than does a simple interpolation of radiosonde temperatures. In this equation, z 850 and z 700 are the 850 and 700 mbar pressure levels. The daily temperature at this median elevation, T d, was calculated as the average of the two layer temperatures available each day. A comparison of T d for each of the weather stations with the daily temperature measured at 2100 m on McCall Glacier (on the moraine) for May—September 1994 is shown in figure 10a; other years show similar correlations. The daily temperature above Inuvik follows that on McCall Glacier most closely, with a correlation coefficient of r 2 = 0.78 for the entire period and r 2 = 0.66 if only positive temperatures are considered (fig. 10b). These correlations are quite good, especially considering the distance to the station. A high degree of correlation also suggests that temperatures on the moraine at McCall Glacier are not affected by local heating. Correlations for Barrow and Fairbanks are not as strong (r 2 = 0.54 and 0.51 for the entire period, respectively). Correlation coefficients of similar magnitude were found by Reference Conway, Rasmussen and HayesConway and others (1995) between temperatures on Blue Glacier (Washington) and those at a nearby radiosonde station, although that station was much closer to the glacier (70 km).
The sum of positive degree days in a given year is obtained from these daily temperatures as

This sum was calculated for all years on record for each of the stations.
As a measure of precipitation on the glacier, we tried the daily precipitation at Inuvik and Barrow. No acceptable correlation was found with the 1994 measurements on the glacier. Because of this, we chose to calculate the annual accumulation on the glacier, A, from the monthly precipitation. P m, at Inuvik or Barrow. This was done in two ways in order to bracket the amount of internal accumulation. First, we summed the “solid” precipitation over l year, beginning with month m 1 in autumn of the previous year. The amount of solid precipitation was estimated using the fraction of clays, N m(T d < 0°C)/N m during the month in which the daily temperature, T d, was below freezing. Here, N m is the number of days in month m. Thus,

The remainder of the total precipitation is assumed to be lost as run-off While this is reasonable for accumulation on temperate glaciers and for surface accumulation in general, net accumulation on Arctic glaciers may be greater as a result of internal accumulation. To allow for this in the mass-balance model, we also used a second, alternative expression for A

In this case, all of the monthly precipitation falling between month m 1 in the previous autumn and month m 2 of the actual balance year is assumed to contribute to the net accumulation. Neither Equation (4) or (5) accounts for the part of internal accumulation that is due to refreezing of surface melt; this latter part depends on summer temperature defined in Equation (3).
Results of the mass-balance model
As staled earlier, both the surface balances and the net balances in Table 2 were used (independently) to calibrate the model. There were two main sets of criteria used to judge the quality of the fit: first, the correlation coefficients between measured mass balance and degree days and accumulation, and secondly, an examination of how well the long-term average annual net balances for the periods 1958–72 (–15 cm) and 1972–93 (–33 cm) were reproduced.

Fig. 10. (a) Average daily temperatures measured on McCall Glacier at 2100 m during summer 1994 compared to the mean temperature of the 700–850 mbar layer over Inuvik, Barrow and Fairbanks. (b) Correlation between the temperatures on McCall Glacier and Td from Inuvik soundings during summer 1994. Only positive temperatures, which enter the positive degree-day sum, are shown.
Additional criteria were used to constrain the solutions, including the physically reasonable assumption that an increase in precipitation at a station should cause a more positive mass balance on the glacier, not more negative.
In order to find the best choices of stations, months of precipitation, and relation between station precipitation and accumulation (Equations (4) or (5)), numerous calibration model runs were conducted. Here, we present only the salient features of these runs, focusing on those which gave the best fits to the data. Parameters for two typical surface balance models using data from Barrow are presented in Table 6, and for Inuvik in Table 7a. In Table 7b, we present similar results for the best net balance models using Inuvik data. The first columns list the equation used to calculate accumulation from P m and the limiting months in Equations (4) or (5), the next four arc- the multi-variable (C multi), single variable (C D for D and C A for accumulation), and cross-correlation (C DA) coefficients (as defined by e.g. Letréguilly, 1988), the next two are the long-term annual balances calculated from the model (for Inuvik, the station record does not completely overlap the 1958–72 time period), and the last two columns are the coefficients c d and c a in the resulting model (Equation (1)).
Table 6. Results of mass-balance model with Barrow data

Table 7. Results of mass-balance model with Inuvik data

Surface mass-balance predictions for the best-fit model over the entire span of the station data are shown in figure 12a for Barrow, and in Figure l2a for Inuvik. The models shown are those for which Equation (5) is used to define the D to A relationship, with parameters given in the first row in Table 6 and 7a. The shaded band in these figures is the error in the solution obtained by assuming variations of 15% in D and A, and an error of ±8 cm in the measured balances (shown as solid circles). A smoothed curve through the modeled balances is shown as a light line in each figure; and this curve illuminates any trends. The input data for each model are shown in Figures 11b and 12b, respectively. figure 12c shows the modeled net balance using the Inuvik data and Equation (4) (the first row in Table 7b).

Fig. 11. Barrow data: (a) Modeled, Equation (4) and m1 = 8, and measured surface mass balance of McCall Glacier. Measured long-term balance is given for comparison. (b) Per-cent deviations from 1951–95 mean of annual degree-day sum D and solid precipitation A. Modeled values are represented by open symbols connected with solid lines, while those measured on McCall Glacier are represented by solid symbols.

Fig. 12. Inuvik data: (a) Modeled surface balance, using Equation (4) and m1 = 8, and measured annual surface mass balances of McCall Glacier. Measured long-term balance is given for comparison. (b) Per-cent deviations from 1961–95 mean of annual degree day sum D and solid precipitation A. Modeled values are represented by open symbols connected with solid lines, while those measured on McCall Glacier are represented by solid symbols. (c) Modeled net balance, using Equation (4), m 1 = 8, and measured annual and long-term net balances of McCall Glacier.
We describe results from each of the model runs in turn:
(1) Barrow. At a first glance, some of the correlations using the Barrow data seem to be significant. However, the degree-day correlation coefficients are small (C D < 0.28), implying that the balance is not strongly correlated with temperature. This is unexpected for McCall Glacier. More importantly, there is a negative correlation between surface balance and accumulation — not a physically realistic prediction. In addition, the modeled long-term average net balances of –89 cm for 1958–72 and –57 cm for the 1972–93 period are much more negative than the measured values (–15 and –33 cm, respectively). Also, the long-term trends in balance do not agree with those in the degree day sums (cf. fig. 11a and b). Thus, we conclude that there is no significant and realistic correlation between Barrow climatological data and the mass balance of McCall Glacier.
(2) Inuvik. The correlations of Inuvik data with the balance on McCall Glacier are generally good, especially when the most reasonable months are used as starting and ending dates in Equations (4) and (5). Based on the sonic-ranger data and our observations in the field, accumulation for the balance year begins in mid-August and ends in June. Thus, we would expert that m 1 = 8 in Equation (4), and m 1 = 8 and m 2 = 6 in Equation (5). Models with these values of m 1 and m 2 give the best fits to the measured balances, although a variation of ± 0.5 month in these parameters docs not change the correlation a great deal. There is a strong negative correlation between balance and Inuvik degree days (C D = –0.8), and a somewhat weaker, but positive (and, therefore, physically meaningful i correlation with Inuvik precipitation (C A = 0.3–0.4). If the net balances in Table 2 are used to calibrate the model, then the modeled long-term average net balances are –18 ± 4 cm and –32 ± 3 cm for 1961–72 and 1972–93, respectively. This is in excellent agreement with measured long-term net balances. The trends in balance and the estimated degree-day sums also agree well with the measured values, as shown in figure 12a–c. We conclude that the climatological variables at Inuvik are significantly correlated with the balance on McCall Glacier, and that they can be used to model the balance as a function of time. Equations (4) and (5) gave similar results for the model parameters and correlation coefficients and, thus, they both appear to be useful in defining the precipitation–accumulation relationship.
The correlation coefficients between the McCall Glacier mass balance and climatological parameters from Inuvik are similar to what Pelto (1996) found in his study of eight North Cascade (Washington) glaciers. He found that correlation coefficients between balance and ablation-season temperature were between 0.68 and 0.84, while the correlation with accumulation-season temperature (a measure of winter precipitation for those glaciers) was between 0.35 and 0.59.
(3) Kaktovik. Unfortunately, the climatological record at Kaktovik, 100 km to the north ends in 1988, so we can only use four of the measured balances in Table 2 to calibrate a model using these data. In order to determine whether such a limited calibration is meaningful, we first attempted it using the 1969–72 sub-set with the Inuvik data, which, as has been shown above, gave good results with the full balance set. The calibration with the Inuvik sub-set showed a consistently good correlation using Equation (5) and the long-term balances were also in good agreement with those listed in Table 7a, implying that the reduced calibration set can produce meaningful results.
Applying this limited calibration method to the Kaktovik data, we obtain ±15 cm for the average annual surface balance from 1958 to 1972 and –35 cm for 1972–88. These results for Kaktovik show the correct qualitative trend towards more negative balances but they are otherwise quite different from the corresponding measured values and from the Inuvik model results. We also compared the annual balances from 1961 to 1988 predicted by the Inuvik model and those using Kaktovik data. The correlation between the two was poor. We conclude that despite its closer proximity, Kaktovik is considerably less suitable than Inuvik for modeling the mass balance of McCall Glacier. Reasons for this are given below.
(4) Fairbanks. Replacing the degree-day sum in the Inuvik model with the sum for Fairbanks causes a general drop in correlation and increases the misfit between measured and modeled long-term mass balances. However, the correlations and the modeled long-term values are superior to those from Barrow or Kaktovik. This implies that, while climate change in interior Alaska is clearly different from that at McCall Glacier, these differences are less pronounced than those between McCall Glacier and the two Arctic coastal locations.
Discussion
The excellent correlation of the McCall Glacier mass balance with climatological parameters from Inuvik, 430 km to the cast, suggests this glacier can provide a climatic index for this part of the Arctic. The trend over the last four decades towards increasingly negative balance is likely caused by a synoptic scale (~ 500–1000 km) climate change.
It is interesting to compare this synoptic-scale representivity with that over a larger scale (≥ 1500 km) across the Arctic. Mass-balance records from other high northern latitude glaciers (summarized by Reference Cogley, Adams, Ecclestone, Jung-Rothenhäusler and OmmanneyCogley and others (1995, Reference Cogley, Adams, Ecclestone, Jung-Rothenhäusler and Ommanney1996)) do not confirm an Arctic-wide trend in the climate. In fact, the 35 year long mass-balance record of White Glacier, the main focus of Cogley and others’ study, shows no significant trend. The White Glacier record, measured about 1500 km to the northeast of Inuvik, shows no correlation with climatological parameters from Inuvik nor with the balance of McCall Glacier. The difference in trends between McCall and White Glaciers is further illustrated by a comparison of their long-term balances, calculated for White Glacier from data presented by Reference Cogley, Adams, Ecclestone, Jung-Rothenhäusler and OmmanneyCogley and others (1995): from 1958 to 1972, the average balance on McCall Glacier was –15cm and on White Glacier (from 1960 to 1972) it was 12 ± 4 cm. From 1972 to 1993, it was –33 cm on McCall Glacier, while on White Glacier it was much less negative (–10 ± 3 cm) from 1972 to 1991.
The poor correlation between the McCall Glacier mass balance and climatological parameters from Barrow and Kaktovik implies that climate-change patterns have been different at these Arctic locations. To reveal these different patterns, in Figure 13 we compare smoothed time series of D and A for the different stations and up to 45 years duration. The positive degree-day sum (fig. 13a) shows a regular pattern of maxima and minima, superimposed on a linear warming trend. The period of the oscillations is not well-resolved but it was estimated to be about 18–20 years for Barrow and Kaktovik, and about 16 years for Fairbanks and Inuvik. Accumulation (fig. 13b) shows an overall trend toward smaller values with a less well-defined cyclic pattern. There was an anti-correlation between winter precipitation and summer temperature at Barrow and Kaktovik. Such an anti-correlation has also been observed between the mean annual temperature and winter precipitation at these two stations (Zhang and Osterkamp, 1993) but it is contrary to the generally accepted idea of a coupled increase in temperature and precipitation in the Arctic (e.g. Reference Houghton, Filho, Callander, Harris, Kattenberg and MaskellHoughton and others, 1996). Inuvik shows smaller oscillations in A that are more in phase with those in D, further illustrating the difference between the climate al McCall Glacier and Inuvik and that at Barrow and Kaktovik.

Fig. 13. Smoothed (Gauss filter of width 2.5 a) annual degree day sum at 2100 m elevation (a) and solid precipitation (b) as calculated from Inuvik, Barrow, Kaktovik and Fairbanks data.
It is interesting that the McCall Glacier mass balance and the climatological variables at Kaktovik, only 100 km away, are poorly correlated, while conditions at locations that are several hundred kilometers apart from another (such as McCall Glacier and Inuvik, and Barrow and Kaktovik) are well correlated with one another. We propose that these correlations are related to the mean summer position of the Arctic Front. Barry (1967) has compiled the Statistics on the summer position of the Arctic Front over North America for a 5 year period. He found that the mean summer temperature of an Arctic region is related to its mean frontal position. In particular, the front always lies to the south of White Glacier in the Canadian Arctic and that glacier is therefore truly Arctic in regime. Barrow and Kaktovik were both north of the mean frontal positions for all 5 years, while the front was north of Inuvik and McCall Glacier about 65% of the summers.
Changes in climate may be related to corresponding displacements in the mean summer position of the Arctic Front. This would synchronously affect regions located along the length of the front in an east–west direction for possibly several hundred kilometers, and possibly cause similar climatic changes parallel to it (such as Inuvik and McCall Glacier or Barrow and Kaktovik). Locations separated in a north–south direction, normal to the front, may experience differing climate changes, even if they are relatively close together (e.g. McCall Glacier and Kaktovik). Further evidence for the importance of the Arctic Front has been given by Scott (1992), who showed that mean summer temperatures at tree line in Canada are significantly correlated with the magnitude of the characteristic change in air temperature that marks the passage of the front in spring.
Other factors may also cause the climate of the coastal stations to differ from those located some distance inland (McCall Glacier and Inuvik), such as summer sea-ice conditions. However, our calculations of degree days involve temperatures measured 1000+ m above the ground and, therefore, local phenomena such as coastal fog cannot be directly linked to differences in D.
Conclusions
We have determined an internally consistent mass-balance record for McCall Glacier for the years 1969–72 and 1993–96. The 1970s data were re-evaluated under the same framework as the 1990s data. Separate records of surface mass balance and net balance, which include internal accumulation, were compiled. Average surface balance was –29 ± 3 cm from 1969 to 1972, and –63 ± 3 cm during the period 1993–96. The corresponding annual net balances were about –19 and –43 cm, respectively. This pronounced trend towards negative mass balances is confirmed by long-term average net balances, which were determined from topographical volume changes: –15 cm from 1958 to 1972, and –33 cm from 1972 to 1993. The gradient of the surface mass balance with elevation increased by 17% between the periods 1969–72 and 1993–96.
Net mass balance is consistently about 25–30% more positive than the surface balance on McCall Glacier, a result of internal accumulation in the cold firn and ice. In the years 1969–72, about 50% of the net accumulation was internal, while during the period 1993–96 almost all of it was internal. A direct comparison of the average surface balance from 1993 to 1994 with the corresponding net balance determined by repeat surveys of glacier-surface elevation gave an average internal accumulation of +22 ±13 cm a−1 for this 2 year period, which again was most of the net accumulation.
Long-term average net balances over the periods 1956–93 and 1972–93 for McCall Glacier and ten other glaciers in the northeast Brooks Range were determined by comparison of 1956 and 1973 photogrammetric maps with surface-elevation profiles made in the 1990s. The glaciers revealed a broadly similar pattern of negative annual mass balances, most of which (including McCall Glacier) were about –30 cm. A few of the glaciers showed somewhat more negative mass balances of about –50 cm. The amount of thinning, as a function of elevation on McCall Glacier, was also roughly similar to that observed on the other glaciers. This implies that the mass balance of McCall Glacier is representative of the glaciers in this region.
Mean retreat rates and fractional length changes were also measured for these 11 glaciers. They show a more complicated regional pattern than the mass balances, with some glaciers showing a concomitant retreat with the ongoing thinning, and others showing little retreat under similar thinning. The differences in retreat rate and fractional length change are probably caused by differences in glacier geometry, especially near the termini.
The measured mass-balance record of McCall Glacier shows a significant correlation with climatological parameters from Inuvik, 430 km to the east. A mass-balance model, based on this correlation, indicates that the trend toward more negative balances is due primarily to an increase in summer temperatures, and secondarily to a simultaneous reduction in precipitation.
While there is a good correlation between McCall Glacier’s mass balance and climate data from Inuvik, there is no reasonable correlation with climatological parameters from Barrow, 550 km to the northwest, Kaktovik, 100 km to the north, or from Fairbanks, 650 km to the south. We interpret the presence or absence of correlations between each of these stations and McCall Glacier, and between the stations themselves, as being determined by their locations relative to the mean summer position of the Arctic Iront.
We conclude that the mass balance of McCall Glacier is representative on both a regional scale and a larger (500 + km, or synoptic) scale. As such, the McCall Glacier mass-balance record is an important measure of ongoing climatic change in the Arctic.
Acknowledgements
This study was supported by gram NSF-OPP-9214954 as part of the LAII program. We wish to thank G. Adalgeirsdóttir, U. Adolphs, J. DeMallie, S. Campbell, J. Sapiano, K. Swanson, D. Trabant and C. Trabant for help in the field, and to Tazlina for providing an especially entertaining field season in 1994. Special thanks are given to D. Trabant and C. Benson for access to their data and for stimulating conversations, and to W. Harrison, M. Sturm and two anonymous reviewers for their helpful comments. We are also grateful to the refuge manager and personnel of the Arctic National Wildlife Refuge for providing valuable assistance.






















