Mathematical Models of Ice Shelves

Abstract

For flat external ice shelves, expanding freely in all directions, the problem of thermodynamics is one-dimensional. In the affine dimensionless system of coordinates, equations of the dynamics together with the rheological equation lead to the non-linear integro-differential equation involving the reduced temperature. In the quasi-steady case the boundary problem for this equation is solved by means of the method of combining asymptotic expansions. It is shown that if ice is coming from the upper and lower surfaces in the opposite directions the regime is unsteady because of the internal heat accumulation.

The integro-differential equation for the temperature in the case of thinning internal ice shelves is more complicated, but it can be solved by a method analogous to the one mentioned above.

Résumé

Pour des plateformes de glace externes plates, s'étendant librement dans toutes les directions le problème thermodynamique est uni-dimensionnel. Dans un système de coordonnées affine sans dimensions, les équations de la dynamique combinées avec l'équation rhéologique conduisent à une équation i ntegro-différentielle non-linéaire concernant la température réduite. Dans le cas d'un état quasi-siationnaire, le problème des limites pour celle équation est résolu en associant des développements asymploliques. Ou montre que si La glace arrivant au voisinage des surfaces inférieures et supérieures provient de directions opposées, le régime est instable à cause de l'accumulation internede chaleur.

L'équation integro-différentielle pour la température dans le cas de plateformes de glace internes amincissantes est plus compliquée, mais la marche de la solution est analogue à celle mentionnée ei-dessus.

Zusammenfassung

Für flache, äusscre Schelfeise, die sich allseits frei ausdehnen können, genügt ein eindimensionales thermodynamisches Modell. Im affinen, dimensionslosen System der Koordinaten führen die dynamischen Gleichungen zusammen mit der reologischen Gleichung zur nirhtlinearen Integro-Differentialgleichung für die reduzierte Temperatur. Im quasi-slationären Fall lässt sich das Randwertproblem für diese Gleichung mit Hilfe der Nahtmethode, verbunden mit asymptotischer Fortsetzung lösen. Es wird gezeigt, dass für den Fall des Eiszustromes von der Ober- und Unterseite in entgcgengesetzter Richtung das System infolge der Ansammlung innerer Wärme instationär wird.

Die Integro-Differentialgleichung für die Temperatur im Falle von ausdünnenden, inneren Schelfcisen ist verwickelter, doch lässt sie sich mil ähnlichen Methoden lösen wir die oben genannte.

Introduction

Floating glaciers are flat slabs which become gradually thinner near the edge, but they combine a horizontal surface, like that of ice divides, with a high velocity, a fact that sharply distinguishes them from the latter. Both these peculiarities result from the absence of tangential stresses on the free lower surface. Except for the internal edges adjacent to the land, all the remaining surfaces of the floating glaciers are free. Therefore, in the three-dimensional orthogonal coordinate system with the axis Oζ normal to the upper and lower surfaces, no tangential stresses are present at all, since the normal stresses coincide with the coordinate axes. But the curvatures of the upper and lower surfaces k _i and k _i are negligibly small due to the flat shape of floating glaciers, so conditions are very favourable for applying the method of a thin boundary layer, and the model is simplified by the absence of horizontal tangential stresses (σ _i ζ = o). Nevertheless, the other four components of the stress tensor may have values of the same order in the general case, so that the dynamics is described by a statically undeterminate system of equations. On the other hand, the conditions are, as a rule, complicated by an essential non-isothermality. Therefore, one should distinguish various types of floating glaciers according to their dynamics, described by different models. In this paper the symbols are mainly as in the previous paper (Grigoryan and others, 1976) so no list of symbols is provided here.

Fig.1 . Coordinate systems

Let us direct the horizontal axis Oξ of the affine system of dimensionless coordinates along sea-level from the internal to the external boundary of the glacier (in the direction of the ice motion), and direct the vertical axis Oζ upward ( Fig. 1). The characteristic linear horizontal dimension L exceeds considerably the average thickness H, so that

(1)

The glacier is bounded by the upper and lower surfaces, ξ = Z ₁(τ) and ξ = Z ₂(τ) respectively (τ being the dimensionless time). The density of ice is p, the density of water is p _w.

Due to the relatively small thickness of the glacier given by Equation (1), the floating layer of ice must be in a local equilibrium along the vertical

(2)

External ice shelves are ones which border upon the shore along one edge only, and at some distance from the shore can expand freely in all directions like drifting tabular icebergs. In these cases the slopes of both upper and lower surfaces as well as the horizontal variations of temperature and of accumulation and ablation rates are as a rule so small that they can be considered with sufficient accuracy as flat plates without any physical differences between the directions in the horizontal plane, with the exception that strains lead to motion relative to the fixed edge.

I. External Ice Shelves

I. Fundamental equations. Formulation of the problem

The system of equilibrium equations for the case in which there is a negligibly small contribution from the inertia] terms is of the form:

(3)

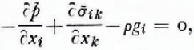
where p is the pressure,

are the stress deviator components, gi is theith component of the acceleration due to gravity. The boundary conditions of the problem are:

(4)

(5)

where τ is the reduced temperature. Equations (4) represent the conditions on the free surface bordering the air; Equations (5) are the conditions at the contact with the water when the viscous coupling forces of water are neglected.

The second boundary conditions in each of Equations (4) and (5) under the condition given by the inequality in (I) lead to the fact that the horizontal tangential stress in a floating glacier is absent to an accuracy of the terms of a higher order of small quantities, whereas the horizontal stresses are equivalent to

(6)

As a result, taking into account the horizontality of the ice surfaces, the following two equations are alone retained from the system of Equations (3):

(7)

The incompressibility equation should be also added; taking account of Equations (6) it acquires the form

(8)

and also the heat-transfer equation (Grigoryan and others, in press) (neglecting the horizontal variation in temperature)

(9)

and the rheology relations (the power flow law), which in dimensional form may be written as

(10)

We also write the expressions for the components of the strain-rate tensor

(11)

So far as ice is incompressible, owing to the Equation (6) we have

(12)

The kinematic conditions of the boundary displacements are:

(13)

(14)

where a, and a, are the accumulation rates at the upper and lower boundaries respectively. The combination of equations and the boundary conditions (7)-(14) defines completely the problem of the thermodynamics of a floating ice shelf.

2.Solution of the dynamical problem

Integration of Equations (7), taking into account the first equations of the conditions (4) and (5), results in the relations:

whence due to Equation (12) we obtain

(15)

Where f is an unknown function of the argument ξ.

The expression for the intensity of the shear stresses, taking account of Equation (12), is

(16)

Consider now the conditions at the contact of the glacier with water (Grigoryan and others. in press):

(17)

Where τ₁ and ₂, are the temperatures of air and water, respectively. From the second equation in (6) taking into consideration Equation (12), we get

(18)

Consequently, at the marginal ice cliff there arises a horizontal tensile stress which reaches the maximum value pgH(I-p/p_w)Z/3σ₀ at the water level (water Z = Z ₁ - Z ₂) and which decreases linearly down to zero at the upper and lower edges of the ice cliff. Therefore, at the ice cliff there arises the torque of moment:

which is equilibrated by a complicated stress in the marginal part of the glacier. However, at some distance from the ice cliff the stress in the ice layer is distributed so that a uniform rate of the horizontal extension of the ice slab in the vertical cross-section is provided

(Weertman, 1957)

(19)

These are constant in the whole slab and change in time only with the variation of Z. The average value of the extending stress in the vertical cross-section is

(20)

It follows from the conditions (13) and (14) that, provided the ice layer is in equilibrium,Equation (2), the vertical velocity v_ξ depends on the vertical coordinate and the accumulation rates as

(21)

From the rheology, Equation (10), we get

(22)

where = I - τ, ≤ < I. So far as e, and e₃ are independent of the coordinate ζ, then

The constant C can be readily determined if we know the expression for the average value of the vertical stress from Equation (20). Thus

(23)

3.Temperature regime of a glacier

The substitution of Equations (21), (22) and (23) into the heat-transfer equation (9) results in the integro-differential equation for the steady case:

(24)

where

(25)

Equation (24) describes the quasi-stationary temperature field T(,τ) = I-(τ) _τ) in the glacier (inasmuch as the dimensionless time τ is inserted in the equation parametrically). The boundary temperature conditions follow from the conditions (4) and (5)

(26)

(27)

The method of solving the boundary problem (24), (26), (27) is based on the fact that the value δ_c is small for ice shelves

,

While f_I = O<(I)

As a result, this problem falls into the class of singular boundary problems, for which the methods of solution are fairly well studied (Cole, 1968). We shall search for a solution of Equation (24) for the main bulk of ice, proceeding from the expansion of the solution in a power series of the small parameter δ _c.

(28)

with the boundary condition (26), and with the boundary condition (27) for the boundary layer. It is necessary to match the solutions at the contact of the boundary layer and the internal region. The evolution of the solution is as follows.

It should be first noted, that the distribution of temperature with depth depends essentially on the pattern of flow lines in the glacier in other words, the solution of Equations (24), (26), (27) depends on the ratio of the values occurring in the expression for the velocity, Equation (21). There are two ways the vertical velocity can change with depth:

(29)

or

(30)

If we first consider (A) the case of (29), i.e. when melting occurs at the lower surface of the glacier (a₂ < 0, ϵ₃ Z ₂ < pa₁/p_w). The substitution of the expansion (28) into Equation (24), after reducing the similar terms at the same powers of S_c, results in a sequence of differential equations

(31)

where it follows from the condition (29) that U > 0. The boundary conditions for the system (31) are:

(32)

The solution for the zero approximation is, thus, of the form:

(33)

Since ξ ≤ Z _1, it is clear that with a decrease of ξ the value _o increases, i.e. the temperature decreases from the lower surface to the upper one.

The totality of solutions of differential equations (31), which, when they are summed, gives the expansion (28), does not satisfy the boundary condition (27). Consequently near the boundary ξ = Z ₂ there inevitably arises a boundary layer with a large temperature gradient so that on its lower boundary the temperature satisfies the condition (27).

In order to retain the "governing terms", i.e. the summands with derivatives, we introduce the boundary layer in the following way:

(34)

Consider the inner expansion in this layer:

(35)

Due to Equation (29) the following relations hold true

The insertion of the expansion (35) into Equation (24), after the similar terms are reduced, leads to a sequence of differential equations

(36)

where The boundary conditions for this sequence of equations follow directly from the condition (27), taking (34) into consideration:

(37)

The solution for the zero approximation of the inner expansion is given by the formula:

The constants C₁ C₂ are obtained from the boundary condition at x _* = O, and also from the condition of "matching" the solutions (28) and (35); the last operation may be carried out most simply by "matching" the terms of the same order separately at the internal limit. The matching of the zero-order terms of the expansion is;

(38)

The conditions (37) and (38) give the final form of the solution of the problem (24)-(27) in the first approximation:

(a) in the region of the boundary layer of the order of δ_e (of the thickness O(δ_e)):

(39)

(b) in the main region the solution is given by Equation (33). The solution, Equations (33) and (39), is obtained to an accuracy of the terms of the order of S,. and of a higher order.

This solution may be specified from the corresponding systems of Equations (31) and (38). The temperature curve corresponding to Equations (33) and (39) is shown in Figure 2.

Fig.2 . Temperature profile when melting occurs at the bottom.

Next let us consider (B) the case (30), i.e. when freezing occurs on the lower surface of the glacier (a₂ > o, pa₁/pw < €₃ Z ₂). Inside the ice layer there is a line, where the vertical velocity changes its sign. In this case two regions of the expansion (28) are distinguished; in the upper one ξ_* < ξ ⩽₁ the solution _o has the form of Equation (33), whereas in the lower one we have, respectively:

(40)

Thus, the temperature increases from the lower surface to ξ_* and decreases from ξ_* to Z ₁. The matching of the branches (33) and (40) can be performed with the help of the boundary layer

(41)

Since inside this boundary layer function U has the expansion

the substitution of an expansion like Equation (35) into Equation (24), taking into consideration Equation (41) and the differential relations d/d ξ = d/ξ_e ¹dx, d²/dξ² = d²/_edx² with regard to Equation (21), results in the system of equations

(42)

The solution for the zero approximation ^* is

(43)

Fig.3. Temperature profile when freezing occurs at the bottom.

Constants B ₁ and B ₂ are determined from the conditions of matching with the branches of Equations (33) and (40) at the inner limit (Cole, 1968). The curve of the temperature distribution in depth is shown in Figure 3. When the temperature function has been determined, the value I can be found from the transcendental equation, which is obtained by substituting Equation (33) or (40) into the first equation of (25):

(44)

4.Conditions of the thermal stability of a glacier

It may be seen, when comparing the results presented in Figures 2 and 3 with the data available, that the majority of external ice shelves have temperature distributions which fall into the case (A) of the preceding section. This means, that the vertical velocity of the ice motion according to Equation (29) displaces ice particles from the upper surface through the whole layer to its lower surface. The dissipative heat generated in this case is transferred from the upper to the lower layers by this advection velocity. Since the dissipative heat-generation coefficient is rather small (at K = 0.15 cm²ⁿ/year kgfⁿ, v _o = I m/year, p/pw = 0.92, σ_o = 0.5 to I kf/cm², J = 42.7 kgf cm/cal, H = 500 m (Shumskiy, 1969), we obtain f ₂ 10^-4 to 10^-3, the temperature gradient in the main bulk of the ice layer is also small. It increases essentially in the bottom part, where almost all the heat generated is accumulated due to advection, reducing the heat flow into the glacier ^* . Such a regime of the glacier is stable, as it does not cause any fluctuations with increased temperature.

To be more precise, the method of transportation of the dissipative heat is determined by flow lines, for which according to Equations (19) and (21) we have the following relation:

(45)

Whence we get the equation of flow lines

(46)

where A is a constant, and ϵ₃ is determined according to (23). The pattern of the flow lines having regard to (29) is shown in Figure 4.

Fig.4. Flow-line pattern when melting occurs et the bottom.

In those parts of the glacier where there is a horizontal temperature gradient lateral temperature fluctuations may appear due to the advective heat transfer.

The case (B) of the previous section, which is in agreement with the conditions (30), shows the unstable regime of the shelf glacier. Indeed, the generated heat is transferred to the inner surface ζ = ζ+ with the zero vertical velocity (the corresponding picture of the flow lines is shown in Figure 5). Thus, the surface ζ = ζ+ of the change of sign of ν_ζ is the surface of the accumulation of the heat generated in the whole bulk of ice. Though the dissipative heat-generation coefficient is rather small, as has been noted above, the total effect of the heat "collection" during a large period throughout the whole thickness of ice may happen to be considerable for a relatively narrow zone in the neighbourhood of ζ = ζ*. Indeed, with the parameter values given'in this section, the heat generation per cubic centimetre of ice on the average has a value of the order of to^-3 to 10-cal/year (4 × 10³ to 4 × to"² J/ycar). In a narrow zone of accumulation of several tens of centimetres in thickness 0.1 to 1 cal/year cm³(0.4 to 4 J/year cm³) will converge from an ice layer of, for instance. 100 m. At the volumetric heat capacity of ice equal to 0.4 cal/cm³ (1.7 J/cm³) this value is sufficient for the temperature in the zone of heat accumulation to increase up to the melting point and for the ice-water phase transition to begin over a period of several years. The role of the conductive heat

Fig.5. Flow-line pattern when freezing occurs at the bottom.

outflow from (he accumulation zone is comparatively small: when the heal conduction coefficient of ice is = 5 × 10 ³cal/cm s, the specific heat capacity is c 0.45 cal/g, and the density is p = (0.90 to 0.92) g/cm³ then the effective radius of the conductive heat outflow per a year will be:

(47)

However, the advection directed against the conductive heat outflow "locks" the heat in the limits of the accumulation zone; the effect of the conductive heal removal almost vanishes, since the radius of the advective transport of heal is:

(48)

and at v ≈ (1 to 2) m/year, r _e ≈r _a.

The thickness of the accumulation zone is determined from the condition of equivalence of the conductive and convective transport of heat and comprises some tens of centimetres, as has been already mentioned above.

The temperature regime of ice shelves was considered by Zotikov (1964). However, he only analysed the temperature distribution in depth, without considering the dynamics of ice (the vertical velocity in the heat-transfer equation was given parametrically) and the heat-generation effect.

In that paper a somewhat unexpected conclusion was reached on the possibility of ice motion in the opposite direction from the glacier surface (the so-called S-type field of temperature). This, as has been mentioned above, contradicts the physical nature of the heat accumulation process. The cause of this erroneous conclusion by Zotikov (1964) consists first of all in neglecting the heat-generation effect, that is impermissible in analysing the quasi-stationary field. As a result, on the graph of the S-type temperature curve the necessary maximum is absent in the neighbourhood of the point corresponding to the neutral surface. Indeed, for the temperature gradient in the presence of inner sources of heat q, uniformly distributed through the whole thickness of the glacier, from Equation (80) of Zotikov (1964) considering the expressions for the mass-transfer velocity in case (B)

(w_u and w_i are absolute values of the velocities on the upper and lower glacier surfaces respectively, n = w_lw_u) we obtain the following expression

(49)

Where

With the values of the parameters given above inserted we get p_u = 5 to 25, q = 2.5 to 20, so that q/p_u = 0.5 to 1.2°. Since at I the function I increases extremely rapidly, for glaciers of a sufficiently large thickness (several tens of metres) we have large values of p _u, and then the sign of the derivative dT/dz is determined by the last term in Equation (49). At n I (the vertical velocity turns to zero in the middle part of the ice layer) we have, on the glacier surfaces,

Consequently, the curve of the temperature distribution with depth is similar to that show in Figure 3; it has a maximum in the neighbourhood of the plane

at which the sign of the vertical velocity changes.

Ice melting is inevitable in the zone of heat accumulation during a large lifetime (the duration of the ice passing through the glacier). Since water discharge is impossible, a layer of water should appear in this zone, which is incompatible with the stability of the glacier, subjected, for instance, to the bending stress due to long waves, and so on. Therefore the conclusion must be drawn, that the existence of glaciers with an opposite motion of ice from the glacier surfaces, which in their shape are similar to Dai-parallel slabs, is impossible. Ice formation on the bottom near the inner boundary of the ice shelf is always connected with a considerable variation in thickness and of the boundary conditions in the longitudinal direction, facts that essentially change the regime of" the glacier.

II. Inner Ice Shelves

Ice shelves in bays and internal seas partly border the grounded ice sheet, or land free of ice, and partly the water. The ice motion, as a rule, starts from the grounded ice sheet and is directed towards the marginal cliff, from which icebergs break off. The ice-free shores in the boundary zone produce a retarding eüeel, and outside it they prevent sideways extension. The direction of motion coincides with the direction of the steepest surface slope. In the same direction the variation in temperature and in the accumulation ablation on the upper and lower surfaces of the glacier are observed. The lines of the slope and of motion in the plan present arcs with a negligibly small curvature; provided the axis ξ is oriented along these arcs, we shall get

(50)

In this section the lower surface of the glacier will be taken as the surface ζ = o. The ratio of the longitudinal and transverse horizontal stresses is defined by the shape of shores:

(51)

where w is the angle between the ice-free shores of the bay, or between the directions of the ice discharge from the shores covered by the grounded ice sheet; w > o when these lines diverge approaching the mouth. Usually, the angle w varies within the range

At ω > 45° there appear conditions for a free spreading, which are typical of external shelf glaciers. On the other hand, at ω < —45° the discharge of ice is so hampered, that the bay usually has a grounded ice sheet. From Equation (51) it follows that

(52)

Outside the sea-shore zone the retardation effect produced by shores is absent, therefore

(53)

The Equations (4), (5) (50) and (51) remain valid for the case under consideration, with the only difference that

(54)

Neglecting the curvatures of the upper and lower surfaces of the glacier (k = k,( = o), we assume the coordinate axes to be horizontal, and (he axis ζ vertical. Therefore the equations of quasi-static equilibrium acquire the form

(55)

the equation of the heal-conduction-heat-transfcr-heat-generation becomes

(56)

whereas the equation of continuity and of the components of the strain-rate tensor should be taken in a general form.

So far as the ratio between the longitudinal and vertical normal stresses is now determined by Equation (52) instead of (12), the extending force arising at the marginal cliff is now equal to

(57)

instead of F = _zz, _zz

Since the tangential stresses are absent, at some distance from the marginal cliff the longitudinal extending stress should be distributed, for the present case as well, in such a way that the velocity of the glacier longitudinal extension would not change along

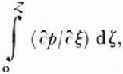By integrating the first and the third Equations (55) over ξ and differentiating the last one over ξ and eliminating the value we obtain

The integration of this equation over f with the boundary condition (57) yields the following equation:

(58)

According to the general equation of kinematics for shifting the boundaries, the vertical velocity component for the two-dimensional case under consideration is expressed in terms of the vertical rate of the compression ₃ =—(I+tanw)₁ and the accumulation rate on the surface by the equations

(59)

Excluding v_it e_,, σ and σ, from Equations (to), (53), (56), (58) and (59), in a power approximation we obtain the following integro-difTerenlial equation for the temperature field

(60)

(61)

The method of solving this equation is analogous to the general method of solving equations with a small parameter at a higher derivative.

After the function (n,T) is found, the strain-rate is determined from the equations

(62)

the strees is found from the equation

(63)

the velocity is determined from Equations (59) and from

(64)

and the velocity of bottom-melting is found from the equation

(65)

The boundary zones of ice shelves adjacent to the ice-free land are distinguished by the fact, that the shear stresses are markedly predominant in them in the vertical surface parallel to the sea-shore. The velocities rapidly increase with distance from the shore due to this stress. The boundary zones are characterized by the following relations:

(66)

Therefore for them the first equation of quasi-static equilibrium acquires the form

(67)

and together with the third equation it gives

(68)

The intensity of the tangential stresses in the first approximation is equal to

(69)

Since the horizontal tangential stresses are absent, the stress ξ is so distributed that the displacement velocity is the same along the vertical;

(70)

The velocity is thus described by the equation

(71)

in which n _o and h are the ordinates of the inner and outer boundaries of the sea-shore zone of displacement. In order to find the temperature distribution it is necessary to solve the equation similar to (60). The values of the normal components of the deviator stress and of the strain-rate tensor are outside die limits of accuracy of the given approximation.