1. INTRODUCTION
Iceberg calving from marine-terminating glaciers accounts for nearly 50% of the mass lost from both the Greenland and Antarctic ice sheets (Jacobs and others, Reference Jacobs, Hellmer, Doake, Jenkins and Frolich1992; Bigg, Reference Bigg1999; Rignot and others, Reference Rignot2008, Reference Rignot, Jacobs, Mouginot and Scheuchl2013; Liu and others, Reference Liu2015). However, the mechanical failure of glacier ice is a complex process owing to the multiscale and multiphysics nature, involving a bewildering variety of deformation and damage mechanisms at various length scales ranging from localized microscale (or milliscale) failure to rifts that exceed hundreds of kilometers. Moreover, because ice can exhibit brittle failure up to the melting point, it is necessary to simultaneously model the slow ductile flow (creep deformation) and fast brittle fracture of glacier ice. A consequence of this complexity is that researchers have not yet agreed on a versatile mathematical model that can be universally implemented in large-scale ice sheet and glacier models to describe fracture and eventual calving behavior (Van der Veen, Reference Van der Veen2002; Bassis and others, Reference Bassis, Coleman, Fricker and Minster2005; Benn and others, Reference Benn, Warren and Mottram2007; Bassis, Reference Bassis2011; Bassis and Walker, Reference Bassis and Walker2012; Bassis and Ma, Reference Bassis and Ma2015). An efficient and applicable mathematical model should be able to reproduce the observed glacier behavior, and easily amalgamate into traditional continuum ice flow models used to simulate decadal to millennial-scale variations in ice dynamics. With this in mind, we develop a continuum-damage-mechanics-based constitutive model for describing the iceberg calving process.
Historically, researchers first sought empirical relations that parameterized the iceberg calving process in terms of a spectrum of internal and external variables that included water depth (Brown and others, Reference Brown, Meier and Post1982; Meier and Post, Reference Meier and Post1987; Hanson and Hooke, Reference Hanson and Hooke2000), ice front thickness (Pfeffer and others, Reference Pfeffer1997), lateral stretching (Alley and others, Reference Alley2007, Reference Alley2008) or a critical height-above-buoyancy (Vieli and others, Reference Vieli, Funk and Blatter2001; Van der Veen, Reference Van der Veen2002). The validity and applicability of these models are limited to a few specific cases. For instance, the water-depth and height-above-buoyancy models are limited to grounded termini only (e.g. Nick and others, Reference Nick, van der Veen and Oerlemans2007, Reference Nick, Vieli, Howat and Joughin2009). Moreover, these parameterizations ignore the physical factors that contribute to the calving process, such as mechanical strain rate and hydrofracture.
It is also possible to attempt to predict the penetration depth (height) of surface (basal) crevasses using various formulations of fracture mechanics (Weertman, Reference Weertman1980; Van der Veen, Reference Van der Veen1998a, Reference Van der Veenb; Benn and others, Reference Benn, Warren and Mottram2007; Plate and others, Reference Plate, Müller, Humbert and Gross2012). Alternatively, the Nye zero-stress model (Nye, Reference Nye1957; Jezek, Reference Jezek1984; Nick and others, Reference Nick, Van der Veen, Vieli and Benn2010) may be used to predict crevasse penetration depths based on the assumption that a crevasse penetrates to the point where horizontal stress vanishes. Calving in these crevasse depth or height-based models is then assumed to occur when the combination of surface and basal crevasses exceeds a critical threshold (e.g. Benn and others, Reference Benn, Warren and Mottram2007; Nick and others, Reference Nick, Van der Veen, Vieli and Benn2010; Bassis and Walker, Reference Bassis and Walker2012). However, these models ignore the viscoelastic effects on failure and assume that introducing fractures, no matter how large, has a negligible effect on the macroscale strain rate or stress field within the glacier or ice sheet. Humbert and others (Reference Humbert2015) used a viscoelastic Maxwell model to compute surface displacements in the Jelbart Ice Shelf in Antarctica and the results matched reasonably well with observations, which emphasizes the need to include viscoelastic effects.
In the recent years, researchers have begun to incorporate the bulk effect of fractures on the deformation of ice using continuum creep damage mechanics, which describes the gradual time dependent failure of the material around pre-existing defects, rather than an abrupt failure described by fracture mechanics approaches. Pralong and others (Reference Pralong, Funk and Lüthi2003) and Pralong and Funk (Reference Pralong and Funk2005) proposed creep damage-based models and used them to analyze the detachment of a hanging glacier, assuming that ice behaves as an incompressible viscous fluid. Duddu and Waisman (Reference Duddu and Waisman2012, Reference Duddu and Waisman2013) and Duddu and others (Reference Duddu, Bassis and Waisman2013) extended these models to include viscoelastic effects and to ensure thermodynamic consistency using the nonlocal damage formulation in a Lagrangian finite element framework. Krug and others (Reference Krug, Weiss, Gagliardini and Durand2014) sought to combine damage and fracture mechanics approaches to model the calving behavior of ice sheets using damage mechanics to predict the ‘starter crack’ depth needed to initiate brittle failure.
Studies have also attempted to apply the formalism of damage mechanics to simplified thin-film formulations of ice-shelf dynamics. For example, Albrecht and Levermann (Reference Albrecht and Levermann2014) proposed a two-dimensional (2-D) ‘fracture density field’ that is in the same spirit as damage mechanics, but uses a phenomenological/empirical parameterization of rifts and fractures in ice shelves. Similarly, Keller and Hutter (Reference Keller and Hutter2014a) introduced a conceptual model of damage in ice shelves, pointing out that even in thin film approximations, damage remains 3-D. These so-called ‘forward’ approaches sought to predict the evolution of damage using numerical models. Following an inverse approach, Borstad and others (Reference Borstad2012) used satellite observed surface velocities to estimate damage in ice shelves. Because this study was diagnostic, Borstad and others (Reference Borstad, Rignot, Mouginot and Schodlok2013) were unable to describe the physical mechanisms behind damage evolution, but they found that, in contrast to the assumptions of fracture-mechanics-based studies, the flow of ice was substantially influenced by the presence of damaged regions of ice.
A key advantage of damage mechanics is its compatibility with the finite-element method (FEM) for simulating fracture propagation in 3-D without having to explicitly track the fracture surface. However, a key challenge of this approach is that it is not possible to specify water pressure as a boundary condition on the fracture surface to incorporate the effects of hydrofracture, an effect that observations indicate is crucial. Several studies have hypothesized surface runoff or meltwater in crevasses as driving force in iceberg calving (e.g. Weertman, Reference Weertman1973; Van der Veen, Reference Van der Veen1998a, Reference Van der Veenb) and ocean water intrusion as an important mechanism for basal crevasse propagation (Weertman, Reference Weertman1980). With the exception of Keller and Hutter (Reference Keller and Hutter2014a), who recently attempted to formulate a damage evolution law for 2-D ice-shelf dynamics that heuristically incorporated the effect of water pressure within basal crevasses, few studies have sought to develop damage-based models that incorporate hydrofracture.
In this study, we propose a formulation to incorporate the effects of water pressure in crevasses, based on the principles of continuum damage mechanics and poromechanics. This new approach considers the effect of water pressure inside damaged ice in the crevassed zones as an additional damage effect, which we call ‘hydrostatic damage’. For the sake of proof of concept, we use the viscoelastic constitutive damage evolution model for polycrystalline ice previously proposed (Duddu and Waisman, Reference Duddu and Waisman2012; Duddu and others, Reference Duddu, Bassis and Waisman2013), but we note that the formulation we propose can be used in conjunction with other constitutive damage models. The constitutive model is based on the small strain assumption and the additive decomposition of strain into its elastic and viscous components, which is valid in this context because the total simulation time is relatively small (hours to days) and the accumulated elastic and viscous strain components are reasonably small. The proposed formulation is used to model the propagation of surface crevasses and the simultaneous propagation of surface and basal crevasses in grounded glaciers. The rest of the paper is organized as follows: first, the viscoelastic damage model incorporating the hydrostatic damage effect is presented; second, the physical geometry and boundary conditions are described along with the results from benchmark studies and several representative numerical examples. In the Appendices, we present a simpler, uniaxial derivation of the model unencumbered by the tensor notation that clouds the more general derivation and we show how the model can be applied to the simpler, purely viscous rheologies more commonly used in glaciology.
2. MODEL FORMULATION
In this section, we review the viscoelastic constitutive damage model for polycrystalline ice under dry conditions, previously presented by Duddu and Waisman (Reference Duddu and Waisman2012), and then extend it for wet (saturated) conditions within the framework of Biot's poroelastic theory (Biot, Reference Biot1941, Reference Biot1955). We refer the readers to the Appendices for a simpler derivation based on idealized stress states.
2.1. Viscoelastic rheology of undamaged ice
Assuming small elastic deformations, we additively decompose the total strain tensor ε into elastic and viscous components
where
![]() ${\epsilon} _{{\rm kl}}^{\rm e} $
is the elastic strain (time independent and recoverable) component and
${\epsilon} _{{\rm kl}}^{\rm e} $
is the elastic strain (time independent and recoverable) component and
![]() ${\epsilon} _{{\rm kl}}^{\rm v} $
is the viscous (time dependent and irrecoverable) component. Making the usual assumption that glacier ice is isotropic, owing to its random polycrystalline microstructure, the elastic stress/strain relationship (multi-axial Hooke's law) is given by
${\epsilon} _{{\rm kl}}^{\rm v} $
is the viscous (time dependent and irrecoverable) component. Making the usual assumption that glacier ice is isotropic, owing to its random polycrystalline microstructure, the elastic stress/strain relationship (multi-axial Hooke's law) is given by
where σ kl denote components of the Cauchy stress tensor, E is Young's modulus, ν is Poisson's ratio, δ kl is the Kronecker delta and repeated indices imply summation. The above equation can be rewritten in the form
where the fourth-order elasticity tensor C ijkl is defined as
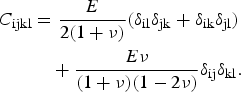 $$\eqalign{{C_{{\rm ijkl}}} & = \displaystyle{E \over {2(1 + \nu )}}({\delta _{{\rm il}}}{\delta _{{\rm jk}}} + {\delta _{{\rm ik}}}{\delta _{{\rm jl}}}) \cr & \quad + \displaystyle{{E\nu} \over {(1 + \nu )(1 - 2\nu )}}{\delta _{{\rm ij}}}{\delta _{{\rm kl}}}.} $$
$$\eqalign{{C_{{\rm ijkl}}} & = \displaystyle{E \over {2(1 + \nu )}}({\delta _{{\rm il}}}{\delta _{{\rm jk}}} + {\delta _{{\rm ik}}}{\delta _{{\rm jl}}}) \cr & \quad + \displaystyle{{E\nu} \over {(1 + \nu )(1 - 2\nu )}}{\delta _{{\rm ij}}}{\delta _{{\rm kl}}}.} $$
Denoting the deviatoric stress,
![]() $\sigma _{{\rm kl}}^{{\rm dev}} = {\sigma _{{\rm kl}}} - {\sigma _{{\rm ii}}}{\delta _{{\rm kl}}}/3$
, the viscous rheology can be expressed using the power-law creep relationship
$\sigma _{{\rm kl}}^{{\rm dev}} = {\sigma _{{\rm kl}}} - {\sigma _{{\rm ii}}}{\delta _{{\rm kl}}}/3$
, the viscous rheology can be expressed using the power-law creep relationship
where A is the temperature dependent viscosity coefficient, n is the flow law exponent, the dot decoration over a variable represents the material derivative and
![]() $\tau _{\rm e}^{\rm 2} = (3/2) \sigma _{{\rm ij}}^{{\rm dev}} \sigma _{{\rm ij}}^{{\rm dev}} $
is the (von Mises) stress invariant. Because in a Maxwell viscoelastic model the stress felt by the viscous and elastic elements is the same, provided that the elasticity tensor does not vanish, the stress can be computed from Eqn (3) and then used directly in Eqn (5) to compute the viscous strain rate.
$\tau _{\rm e}^{\rm 2} = (3/2) \sigma _{{\rm ij}}^{{\rm dev}} \sigma _{{\rm ij}}^{{\rm dev}} $
is the (von Mises) stress invariant. Because in a Maxwell viscoelastic model the stress felt by the viscous and elastic elements is the same, provided that the elasticity tensor does not vanish, the stress can be computed from Eqn (3) and then used directly in Eqn (5) to compute the viscous strain rate.
2.2. Viscoelastic rheology of damaged ice
We assume isotropic damage of ice under tension to simplify the formulation. We introduce a scalar internal state variable D, such that its evolution from D = 0 to 1 represents the deterioration of ice from the fully intact undamaged state to the completely damaged state. For 0 < D < 1, we can define an effective stress
![]() ${\bar \sigma _{{\rm ij}}}$
in the material that is larger than the average stress σ
ij defined by
${\bar \sigma _{{\rm ij}}}$
in the material that is larger than the average stress σ
ij defined by
Following the hypothesis of equivalent strain (Lemaitre, Reference Lemaitre1992), the stress/strain relationship for damaged ice, in terms of the effective stress, can be expressed as
The damage modified viscous strain rate tensor is now defined in terms of the effective stress as
with the effective deviatoric stress
![]() $\bar \sigma _{{\rm kl}}^{{\rm dev}} = {\bar \sigma _{{\rm kl}}} - {\bar \sigma _{{\rm ii}}}{\delta _{{\rm kl}}}/3$
and
$\bar \sigma _{{\rm kl}}^{{\rm dev}} = {\bar \sigma _{{\rm kl}}} - {\bar \sigma _{{\rm ii}}}{\delta _{{\rm kl}}}/3$
and
![]() $\bar \tau _{\rm e}^{\rm 2} = (3/2)\bar \sigma _{{\rm ij}}^{{\rm dev}} \bar \sigma _{{\rm ij}}^{{\rm dev}} $
. Substituting these definitions into Eqn (8), the damage magnified viscous strain rate is
$\bar \tau _{\rm e}^{\rm 2} = (3/2)\bar \sigma _{{\rm ij}}^{{\rm dev}} \bar \sigma _{{\rm ij}}^{{\rm dev}} $
. Substituting these definitions into Eqn (8), the damage magnified viscous strain rate is
Thus, the presence of damage leads to a nonlinear strain rate enhancement factor of (1 − D)−n .
2.3. Effect of pore pressure on the rheology of damaged ice
The previous sections described a constitutive creep damage model for polycrystalline ice, analogous to those developed by Pralong and Funk (Reference Pralong and Funk2005), Duddu and Waisman (Reference Duddu and Waisman2012) and with the exception of the damage production law Krug and others (Reference Krug, Weiss, Gagliardini and Durand2014). In this section, we extend the continuum damage model to incorporate hydraulic fracture under wet (saturated) conditions where water can penetrate into microfractures (Fig. 1). Recalling Biot's theory of poroelasticity (Biot, Reference Biot1941, Reference Biot1955), the relationship between the homogenized Cauchy stress σ
ij and macroscopic solid effective stress
![]() ${\tilde \sigma _{{\rm ij}}}$
under saturated conditions can be defined as
${\tilde \sigma _{{\rm ij}}}$
under saturated conditions can be defined as
where P
h represents the pressure of water filling the pores of a permeable medium, and ϕ is the average porosity of the medium. Assuming that damage and porosity are equivalent in isotropically damaged ice as a first approximation, we can extend the definition of the effective stress
![]() ${\bar \sigma _{{\rm ij}}}$
(defined in Eqns (6) and (7)) to express the homogenized Cauchy stress as
${\bar \sigma _{{\rm ij}}}$
(defined in Eqns (6) and (7)) to express the homogenized Cauchy stress as

Fig. 1. Schematic showing the main features of the model. Surface and basal crevasses are present in the grounded ice.
Note that in the dry case P h = 0 and Eqn (11) reduces to the original definition of effective stress defined in Eqn (6). For simplicity, we further assume that water flow into pores is sufficiently rapid so that the water pressure P h in the microvoids and microcracks in damaged ice is hydrostatic. This implies
where ρ f is the fluid density, g is the gravitational acceleration, 〈〉 denote Macaulay brackets defined such that 〈χ〉 = χ when χ > 0 and 〈χ〉 = 0 when χ < 0, and the hydraulic head z is the vertical distance between the water surface level z 0 and the level of the material point z 1 (i.e. z = z 0 − z 1).
Combining Eqns (12) and (11), we can now write the macroscopic stress/strain relationship as
When D = 0 the above equation for Cauchy stress reduces to that of the undamaged material and when 〈z〉 = 0, that is, when the hydraulic head is below the material point, the equation reduces to that of the damaged material under dry conditions. Note that the effective solid stress
![]() ${\bar \sigma _{{\rm ij}}}$
increases under saturated conditions, as given by
${\bar \sigma _{{\rm ij}}}$
increases under saturated conditions, as given by
The damage modified viscous strain rate tensor under wet conditions is given by
with the effective deviatoric stress
![]() $\bar \sigma _{{\rm kl}}^{{\rm dev}} = {\bar \sigma _{{\rm kl}}} - {\bar \sigma _{{\rm ii}}}{\delta _{{\rm kl}}}/3$
and
$\bar \sigma _{{\rm kl}}^{{\rm dev}} = {\bar \sigma _{{\rm kl}}} - {\bar \sigma _{{\rm ii}}}{\delta _{{\rm kl}}}/3$
and
![]() $\bar \tau _{\rm e}^{\rm 2} = (3/2)\bar \sigma _{{\rm ij}}^{{\rm dev}} \bar \sigma _{{\rm ij}}^{{\rm dev}} $
. Recalling that neither the von Mises stress,
$\bar \tau _{\rm e}^{\rm 2} = (3/2)\bar \sigma _{{\rm ij}}^{{\rm dev}} \bar \sigma _{{\rm ij}}^{{\rm dev}} $
. Recalling that neither the von Mises stress,
![]() ${\bar \tau _{\rm e}}$
, nor the deviatoric stress,
${\bar \tau _{\rm e}}$
, nor the deviatoric stress,
![]() $\sigma _{{\rm kl}}^{{\rm dev}} $
, depend on pore pressure, Eqn (15) shows that unlike the elastic rheology, the viscous component of the rheology is invariant to the inclusion of pore pressure. This is illustrated more explicitly for the uniaxial example in Appendices A and B.
$\sigma _{{\rm kl}}^{{\rm dev}} $
, depend on pore pressure, Eqn (15) shows that unlike the elastic rheology, the viscous component of the rheology is invariant to the inclusion of pore pressure. This is illustrated more explicitly for the uniaxial example in Appendices A and B.
2.4. Damage evolution law
To complete the constitutive damage model description, we need to specify the damage evolution law. There is large uncertainty in the appropriate specification of a damage evolution law, but our formulation in theory is more general and does not depend on the particular choice of evolution law. Nonetheless, for definiteness we adopt a power-law isotropic damage rate function analogous to that was previously introduced by Pralong and Funk (Reference Pralong and Funk2005) and Duddu and Waisman (Reference Duddu and Waisman2012, Reference Duddu and Waisman2013):
where the damage rate coefficient B is a (possibly temperature dependent) model parameter, the exponent r is a chosen constant, the exponent k σ is a stress dependent parameter and χ is the Hayhurst equivalent stress given by Pralong and Funk (Reference Pralong and Funk2005):
In the above equation, α and β are material parameters that control the damage growth mechanism (a detailed discussion on their selection is provided by Pralong and Funk (Reference Pralong and Funk2005)),
![]() ${\bar \sigma ^{(1)}}$
is the largest effective principal stress and
${\bar \sigma ^{(1)}}$
is the largest effective principal stress and
![]() ${\bar \tau _{\rm e}}$
is the effective von Mises stress corresponding to the solid matrix of porous ice. In this paper, we consider that failure occurs due to tensile stresses only so that ice remains intact in compression. Hence, damage only accumulates when
${\bar \tau _{\rm e}}$
is the effective von Mises stress corresponding to the solid matrix of porous ice. In this paper, we consider that failure occurs due to tensile stresses only so that ice remains intact in compression. Hence, damage only accumulates when
![]() ${\bar \sigma ^{(1)}} \gt 0$
. Creep experiments on polycrystalline materials (including metals and ice at high temperatures) illustrate that the rate of creep damage growth increases drastically as we approach full collapse. To be consistent with previous studies (Pralong and Funk, Reference Pralong and Funk2005; Duddu and Waisman, Reference Duddu and Waisman2012) we introduce a stress dependent exponent of the form
${\bar \sigma ^{(1)}} \gt 0$
. Creep experiments on polycrystalline materials (including metals and ice at high temperatures) illustrate that the rate of creep damage growth increases drastically as we approach full collapse. To be consistent with previous studies (Pralong and Funk, Reference Pralong and Funk2005; Duddu and Waisman, Reference Duddu and Waisman2012) we introduce a stress dependent exponent of the form
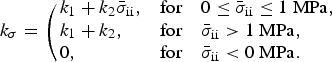 $${k_\sigma} = \left( {\matrix{ {{k_1} + {k_2}{{\bar \sigma} _{{\rm ii}}},} \hfill & {{\rm for}\quad 0 \le {{\bar \sigma} _{{\rm ii}}} \le 1\;{\rm MPa},} \hfill \cr {{k_1} + {k_2},} \hfill & {{\rm for}\quad {{\bar \sigma} _{{\rm ii}}} \gt 1\;{\rm MPa},} \hfill \cr {0,} \hfill & {{\rm for}\quad {{\bar \sigma} _{{\rm ii}}} \lt 0\;{\rm MPa}.} \hfill \cr}} \right.$$
$${k_\sigma} = \left( {\matrix{ {{k_1} + {k_2}{{\bar \sigma} _{{\rm ii}}},} \hfill & {{\rm for}\quad 0 \le {{\bar \sigma} _{{\rm ii}}} \le 1\;{\rm MPa},} \hfill \cr {{k_1} + {k_2},} \hfill & {{\rm for}\quad {{\bar \sigma} _{{\rm ii}}} \gt 1\;{\rm MPa},} \hfill \cr {0,} \hfill & {{\rm for}\quad {{\bar \sigma} _{{\rm ii}}} \lt 0\;{\rm MPa}.} \hfill \cr}} \right.$$
2.5. Mechanical equilibrium
Assuming small deformations, the mechanical equilibrium can be described by the standard viscoelastic boundary value problem in the computational domain Ω as
where b
i is the body forces vector;
![]() ${\bar u_{\rm i}}$
denotes any prescribed displacement conditions corresponding to free slip or zero slip on the domain boundary Γu,
${\bar u_{\rm i}}$
denotes any prescribed displacement conditions corresponding to free slip or zero slip on the domain boundary Γu,
![]() ${\bar t_{\rm i}}$
denotes any prescribed traction conditions corresponding to seawater pressure on the domain boundary Γt; and n
j denotes the outward normal to the boundary Γt. Equation (19) is the static equilibrium equation in solid mechanics, which resembles the stationary Stokes approximation from the fluid mechanics point of view. The viscous strain
${\bar t_{\rm i}}$
denotes any prescribed traction conditions corresponding to seawater pressure on the domain boundary Γt; and n
j denotes the outward normal to the boundary Γt. Equation (19) is the static equilibrium equation in solid mechanics, which resembles the stationary Stokes approximation from the fluid mechanics point of view. The viscous strain
![]() ${\epsilon} _{{\rm mn}}^{\rm v} $
in Eqn (20) is calculated from the evolution law in Eqn (15), which defines
${\epsilon} _{{\rm mn}}^{\rm v} $
in Eqn (20) is calculated from the evolution law in Eqn (15), which defines
![]() ${\dot \epsilon} _{{\rm mn}}^{\rm v} $
. In Eqn (21),
${\dot \epsilon} _{{\rm mn}}^{\rm v} $
. In Eqn (21),
![]() $C_{{\rm ijmn}}^{{\rm hd}} $
denotes the hydro-damage modified fourth-order elasticity tensor, defined as
$C_{{\rm ijmn}}^{{\rm hd}} $
denotes the hydro-damage modified fourth-order elasticity tensor, defined as
Using the relations C
ijkl
δ
kl = (E/(1 − 2ν))δ
ij = 3κδ
ij and
![]() ${\bar \sigma _{{\rm qq}}} = 3\kappa {\epsilon} _{{\rm pp}}^{\rm e} $
, the above equation can be derived from Eqn (13) as follows:
${\bar \sigma _{{\rm qq}}} = 3\kappa {\epsilon} _{{\rm pp}}^{\rm e} $
, the above equation can be derived from Eqn (13) as follows:
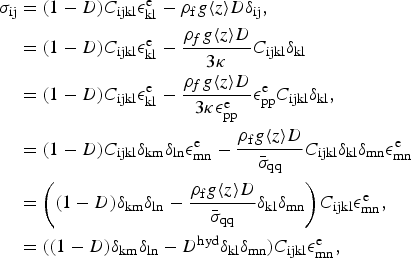 $$\eqalign{{\sigma _{{\rm ij}}} &= (1 - D){C_{{\rm ijkl}}}{\epsilon} _{{\rm kl}}^{\rm e} - {\rho _{\rm f}}g\langle z\rangle D{\delta _{{\rm ij}}}, \cr & = (1 - D){C_{{\rm ijkl}}}{\epsilon} _{{\rm kl}}^{\rm e} - \displaystyle{{{\rho _f}g\langle z\rangle D} \over {3\kappa}} {C_{{\rm ijkl}}}{\delta _{{\rm kl}}} \cr & = (1 - D){C_{{\rm ijkl}}}{\epsilon} _{{\rm kl}}^{\rm e} - \displaystyle{{{\rho _f}g\langle z\rangle D} \over {3\kappa {\epsilon} _{{\rm pp}}^{\rm e}}} {\epsilon} _{{\rm pp}}^{\rm e} {C_{{\rm ijkl}}}{\delta _{{\rm kl}}}, \cr &= (1 - D){C_{{\rm ijkl}}}{\delta _{{\rm km}}}{\delta _{{\rm ln}}}{\epsilon} _{{\rm mn}}^{\rm e} - \displaystyle{{{\rho _{\rm f}}g\langle z\rangle D} \over {{{\bar \sigma} _{{\rm qq}}}}}{C_{{\rm ijkl}}}{\delta _{{\rm kl}}}{\delta _{{\rm mn}}}\epsilon _{{\rm mn}}^{\rm e} \cr &= \left( {(1 - D){\delta _{{\rm km}}}{\delta _{{\rm ln}}} - \displaystyle{{{\rho _{\rm f}}g\langle z\rangle D} \over {{{\bar \sigma} _{{\rm qq}}}}}{\delta _{{\rm kl}}}{\delta _{{\rm mn}}}} \right){C_{{\rm ijkl}}}{\epsilon} _{{\rm mn}}^{\rm e}, \cr & = ((1 - D){\delta _{{\rm km}}}{\delta _{{\rm ln}}} - {D^{{\rm hyd}}}{\delta _{{\rm kl}}}{\delta _{{\rm mn}}}){C_{{\rm ijkl}}}{\epsilon} _{{\rm mn}}^{\rm e},} $$
$$\eqalign{{\sigma _{{\rm ij}}} &= (1 - D){C_{{\rm ijkl}}}{\epsilon} _{{\rm kl}}^{\rm e} - {\rho _{\rm f}}g\langle z\rangle D{\delta _{{\rm ij}}}, \cr & = (1 - D){C_{{\rm ijkl}}}{\epsilon} _{{\rm kl}}^{\rm e} - \displaystyle{{{\rho _f}g\langle z\rangle D} \over {3\kappa}} {C_{{\rm ijkl}}}{\delta _{{\rm kl}}} \cr & = (1 - D){C_{{\rm ijkl}}}{\epsilon} _{{\rm kl}}^{\rm e} - \displaystyle{{{\rho _f}g\langle z\rangle D} \over {3\kappa {\epsilon} _{{\rm pp}}^{\rm e}}} {\epsilon} _{{\rm pp}}^{\rm e} {C_{{\rm ijkl}}}{\delta _{{\rm kl}}}, \cr &= (1 - D){C_{{\rm ijkl}}}{\delta _{{\rm km}}}{\delta _{{\rm ln}}}{\epsilon} _{{\rm mn}}^{\rm e} - \displaystyle{{{\rho _{\rm f}}g\langle z\rangle D} \over {{{\bar \sigma} _{{\rm qq}}}}}{C_{{\rm ijkl}}}{\delta _{{\rm kl}}}{\delta _{{\rm mn}}}\epsilon _{{\rm mn}}^{\rm e} \cr &= \left( {(1 - D){\delta _{{\rm km}}}{\delta _{{\rm ln}}} - \displaystyle{{{\rho _{\rm f}}g\langle z\rangle D} \over {{{\bar \sigma} _{{\rm qq}}}}}{\delta _{{\rm kl}}}{\delta _{{\rm mn}}}} \right){C_{{\rm ijkl}}}{\epsilon} _{{\rm mn}}^{\rm e}, \cr & = ((1 - D){\delta _{{\rm km}}}{\delta _{{\rm ln}}} - {D^{{\rm hyd}}}{\delta _{{\rm kl}}}{\delta _{{\rm mn}}}){C_{{\rm ijkl}}}{\epsilon} _{{\rm mn}}^{\rm e},} $$
where κ denotes the bulk modulus of elasticity and the hydrostatic or hydraulic damage component D hyd is defined as
Evidently, the hydraulic damage D
hyd is nonzero only when there is some existing damage and is proportional to the ratio of the effective fluid pore pressure P
h
D = ρ
f
g〈z〉D and solid matrix pressure
![]() ${\bar \sigma _{{\rm qq}}} = 3\kappa {\epsilon} _{{\rm pp}}^{\rm e} $
. Subjected to plane strain assumptions, the solution to the nonlinear boundary value problem defined by Eqns (19–23) is obtained using the Galerkin FEM detailed by Duddu and Waisman (Reference Duddu and Waisman2012); Duddu and others (Reference Duddu, Bassis and Waisman2013) and Duddu and Waisman (Reference Duddu and Waisman2013). In the present finite element implementation, four-node bilinear quadrilateral elements were used to discretize the unknown displacement field and the four-point Gauss quadrature rule is used for integration. The internal state and history variables (e.g. damage, viscous strains) are stored at the quadrature points and an explicit forward Euler scheme is used to update these variables in time. We note that choosing higher order elements or finer resolutions is generally recommended in case higher accuracy is required.
${\bar \sigma _{{\rm qq}}} = 3\kappa {\epsilon} _{{\rm pp}}^{\rm e} $
. Subjected to plane strain assumptions, the solution to the nonlinear boundary value problem defined by Eqns (19–23) is obtained using the Galerkin FEM detailed by Duddu and Waisman (Reference Duddu and Waisman2012); Duddu and others (Reference Duddu, Bassis and Waisman2013) and Duddu and Waisman (Reference Duddu and Waisman2013). In the present finite element implementation, four-node bilinear quadrilateral elements were used to discretize the unknown displacement field and the four-point Gauss quadrature rule is used for integration. The internal state and history variables (e.g. damage, viscous strains) are stored at the quadrature points and an explicit forward Euler scheme is used to update these variables in time. We note that choosing higher order elements or finer resolutions is generally recommended in case higher accuracy is required.
3. NUMERICAL EXAMPLES
In this section, we demonstrate the numerical results obtained from the finite element simulation of surface and basal crevasse propagation. First, we present a benchmark example to demonstrate the capability of the model to accurately calculate the hydraulic forces on the crevasse walls and the resulting stress field in ice. Second, we investigate the propagation of surface crevasses, as well as the simultaneous propagation of both surface and basal crevasses for different boundary conditions.
3.1. Model geometry and parameters
We idealize the geometry of grounded marine-terminating glaciers as rectangular slabs of ice in contact with water, as shown in Figure 2. We apply a free slip boundary condition in the horizontal direction at the bottom edge of the slab (assuming minimal friction from the bed) and in the vertical direction on the left edge of the slab (where the ice slab is connected to the larger glacier). We apply a fixed (or zero displacement) boundary condition in the horizontal direction on the left edge of the slab. Assuming the influx of ice is independent of depth, this set of boundary conditions is translationally invariant in the horizontal direction and hence independent of the inflow velocity. Furthermore, the choice of zero displacement or velocity boundary condition is justified because we are interested in calculating the stress and deformation rates defined by the displacement or velocity gradients, thus, they are independent of the inflow velocity or displacement condition at the left edge.

Fig. 2. Schematic drawing of the idealized grounded ice slab with dimensions and boundary conditions.
We denote the depth of the surface and basal crevasses by d s and d b respectively, and the initial ice thickness by H. The initial notches play the role of pre-existing weaknesses or starter cracks in linear elastic fracture mechanics and provide the seeds for localized damage propagation. This assumption prevents the growth of non-physical damage areas on the top of the slab in areas where the FEM discretization may be coarse to reduce the computational burden. Alternative crack or damage initiation schemes can be employed (e.g. seeding the glacier with random defects), but our scheme (i.e. seeding crevasses using notches) allows us to easily perform model sensitivity studies (Duddu and Waisman, Reference Duddu and Waisman2013). Additionally, in all the following numerical examples, once damage localizes near the initial notches, we allow hydrostatic (or hydraulic) damage to occur only in the vicinity of the crack path. The slab length L = 2500 m is set to five times the ice thickness H = 500 m and the initial surface or basal crevasses (notches) are prescribed at midlength, to avoid edge effects at the inflow and outflow boundaries. The depths of the initial crevasses (notch) are set to 8% of the initial slab thickness H. The piezometric head or hydraulic head in surface crevasses h s is defined as the height of the water column measured from the top edge of the slab, consequently, the water pressure at the bottom of the surface crevasse is proportional to (h s + d s). We specifically allow for h s > 0 to examine the effect of a supra-glacial lake filling a crevasse, although it simulates an unphysical example because we do not model the lake nor the topography necessary to sustain the lake. The piezometric head at the bottom of the basal crevasse is assumed to be equal to the height of water level on the right edge of the slab denoted by h w. All the relevant material and model parameters listed in Table 1 are assumed from Duddu and Waisman (Reference Duddu and Waisman2012) for ice at −10°C. The homogeneous ice density ρ i = 910 kg m−3 and water density ρ f = 1000 kg m−3. The value of the damage coefficient parameter B in Eqn (16), controlling the damage rate, is varied in the numerical studies so as to assess model sensitivity.
Table 1. Values of mechanical and damage parameters for ice at −10°C
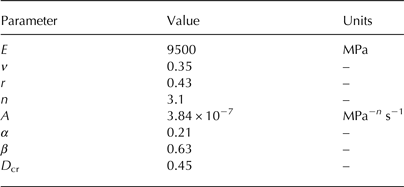
The parameter A is the viscosity coefficient retrieved from Duddu and others (Reference Duddu, Bassis and Waisman2013) by taking A = (3/2)K N; where K N is the viscosity coefficient defined by Duddu and others (Reference Duddu, Bassis and Waisman2013).
3.2. Benchmark simulation
To demonstrate the capability of the proposed damage model to consistently calculate the hydraulic forces on the crevasse walls, we consider a rectangular ice slab (2500 m × 500 m) initialized with a surface and a basal crevasse in two different approaches. In the first approach, the crevasses are defined by notches and the hydraulic forces at the finite element nodes lying on the crevasse walls are calculated from the hydrostatic pressure distribution using the line integral,
![]() $\int_\Gamma {P^{\rm h}}d\Gamma $
, as indicated in Figure 3. Thus, in the first approach the geometrical features of the crevasses are explicitly meshed and the corresponding results provide a reference solution or benchmark. In the second approach, the crevasses are defined by fully damaged elements by specifying D = 1 inside the crevasse zone and the hydraulic forces at the finite element nodes lying on the crevasse walls are calculated from the stress distribution using the area integral,
$\int_\Gamma {P^{\rm h}}d\Gamma $
, as indicated in Figure 3. Thus, in the first approach the geometrical features of the crevasses are explicitly meshed and the corresponding results provide a reference solution or benchmark. In the second approach, the crevasses are defined by fully damaged elements by specifying D = 1 inside the crevasse zone and the hydraulic forces at the finite element nodes lying on the crevasse walls are calculated from the stress distribution using the area integral,
![]() ${\int_\Omega} {\rho _{\rm f}}g\langle z\rangle D{\delta _{{\rm ij}}}d\Omega $
(as given by the second term in Eqn (13)). Thus, in the second approach the geometrical features of the crevasses are implicitly defined by the damage variable and the results are compared with those obtained from the first approach. The following parameters were used in this study: crevasse depths d
s = d
b = 25 m; the piezometric head h
s = 0 and h
w = 0.5H. The total hydraulic forces calculated from both approaches on either side of the crevasse are the same: 3126.9 kN for the surface crevasse and 59 411.8 kN for the basal crevasse. The horizontal stress distributions computed using the two approaches, shown in Figure 4, are identical to within numerical error. Thus, this benchmark investigation indicates that our damage model is capable of accurately describing the stress state of an ice slab with fully damaged crevasse (i.e. when D = 1). This example also demonstrates the main advantage of the continuum damage mechanics description that completely eliminates the need for remeshing as the fracture propagates.
${\int_\Omega} {\rho _{\rm f}}g\langle z\rangle D{\delta _{{\rm ij}}}d\Omega $
(as given by the second term in Eqn (13)). Thus, in the second approach the geometrical features of the crevasses are implicitly defined by the damage variable and the results are compared with those obtained from the first approach. The following parameters were used in this study: crevasse depths d
s = d
b = 25 m; the piezometric head h
s = 0 and h
w = 0.5H. The total hydraulic forces calculated from both approaches on either side of the crevasse are the same: 3126.9 kN for the surface crevasse and 59 411.8 kN for the basal crevasse. The horizontal stress distributions computed using the two approaches, shown in Figure 4, are identical to within numerical error. Thus, this benchmark investigation indicates that our damage model is capable of accurately describing the stress state of an ice slab with fully damaged crevasse (i.e. when D = 1). This example also demonstrates the main advantage of the continuum damage mechanics description that completely eliminates the need for remeshing as the fracture propagates.

Fig. 3. Hydraulic pressure distribution on the surface and basal crevasses, assuming complete ice material failure (D = 1) of the elements in the crevasse zone, which is represented by a notch in this figure. The values of the hydraulic pressure P h are given at the bottom and top of the surface and basal crevasses.

Fig. 4. Snapshot of horizontal stress, σ xx , contours in the linear elastic configuration using two methods; (a) models crevasses as notches and hydraulic forces are applied as nodal forces; (b) represents the equivalent proposed damage mechanics technique and (c) the stress σ xx profile along the slab centerline where the height of the material point is measured from the bottom of the slab.
3.3. Effect of hydrodamage on surface crevasse propagation
We first conducted several simulations to investigate the effect of hydrodamage on the depth d s to which surface crevasses penetrate in relation to the seawater depth h w. We consider three different values of h w/H = {0, 0.5, 0.8} and take h s = 0 to activate hydraulic damage under wet conditions. Figure 5 shows snapshots of damage contours (red zones indicate completely damage ice) for h w/H = 0.8 and damage coefficient B = 10−5 MPa−r s−1. These simulation results emphasize the localized nature of crevasse propagation in glaciers driven by stress concentrations near pre-existing defects. Next, we conducted model sensitivity studies by varying the value of the damage coefficient B = {10−3, 10−4, 10−5} MPa−r s−1 and the corresponding time steps used in the analysis are dt = {0.1, 1, 10}s, respectively. The time step is chosen sufficiently small (on the order of seconds) to ensure accuracy and stability of the explicit time update scheme used for computing damage and viscous strain evolution. Crevasse depths were computed under dry (no hydrodamage – NHD) and wet (hydrodamage – HD) conditions. In Figure 6, the normalized surface crevasse depths (d s/H) are plotted against simulation time (h) for different normalized seawater depths (h w/H). Note that the depth of the surface crevasse d s at a given time is measured as the vertical distance from the top of the slab to the farthest finite element node where the damage exceeds the critical damage value, that is, D >D cr (Table 1). The following conclusions can be drawn from Figure 6:
-
(1) Water-filled surface crevasses experience more damage at any particular time and propagate to greater depths (for a given color compare the solid and dashed curves in Fig. 6), including full-depth fractures indicating calving events (i.e. d s/H = 1); these results conform with Nye zero-stress results in Weertman (Reference Weertman1973) and linear elastic fracture mechanics (LEFM) results in Van der Veen (Reference Van der Veen1998b);
-
(2) The value of the damage coefficient B does not significantly change the final crevasse depth (compare the different colored dashed curves in Fig. 6), but it affects the rate at which crevasses propagates; consequently, it affects the time interval between calving events. However, model predicted damage (or crevasse) propagation rates are poorly calibrated by field or laboratory experiments. This result also demonstrates that the small strain assumption does not influence the conclusions drawn from our modeling studies; because similar crevasse penetration depths are retrieved for the case of B = 10−3 (where the accumulated viscous strains are small) and the case of B = 10−5 (where the accumulated viscous strains are larger).

Fig. 5. Snapshot of damage contours at different time steps for the isolated surface crevasse propagation model with h w/H = 0.8. These results were simulated using B = 10−5 MPa−r s−1.

Fig. 6. The evolution of surface crevasse with time under different values of near terminus water depth h w. The figures show simulation results for different values of B, the parameter in Eqn (16). The tag ‘HD’ in the legend means including Hydraulic Damage and ‘NHD’ means No Hydraulic Damage.
We next performed a sequence of simulations to investigate the stability of marine-terminating glaciers in relation to the piezometric head h
s in surface crevasses. We consider three different values of h
s = {0, 25, 50} m (where h
s >0 corresponds to the presence of a supraglacial lake) and recorded the temporal evolution of surface crevasses for different seawater depths h
w. In Figure 7, we plot the normalized maximum (or final) crevasse depth
![]() $d_{\rm s}^{{\rm max}} /H$
and the total time (h) elapsed till maximum crevasse depth is attained as a function of the normalized seawater depth h
w/H, under dry conditions and under wet conditions for three different values of piezometric head h
s. These simulations illustrate that:
$d_{\rm s}^{{\rm max}} /H$
and the total time (h) elapsed till maximum crevasse depth is attained as a function of the normalized seawater depth h
w/H, under dry conditions and under wet conditions for three different values of piezometric head h
s. These simulations illustrate that:
-
(1) Under dry conditions, through-thickness surface crevasse propagation is not observed, regardless of the seawater level (blue curve in Fig. 7a); whereas, under wet conditions through thickness surface crevasse propagation always occurs except when the seawater level is sufficiently high (h w > 0.8, as indicated by green, red and brown curves in Fig. 7). Thus, meltwater in surface crevasses destabilizes the glacier by driving through thickness crevasse propagation. These conclusions agree with the Nye zero-stress model in Weertman (Reference Weertman1973) that water-filled surface crevasses are highly likely to reach the bottom of the slab.
-
(2) An increase of seawater height generally decreases the rate of crevasse propagation (more pronounced when h w > 0.5 in Figs 6, 7), consequently, it increases the total time elapsed till maximum crevasse depth is attained. Thus, the seawater level has a stabilizing effect on crevasse propagation as it applies a compressive crack-closing pressure. These results provide a qualitative measure of the conditions that lead to faster versus slower crevasse propagation, although the quantitative damage propagation rate remains poorly calibrated.

Fig. 7. Final crevasse depths ratios
![]() $d_{\rm s}^{{\rm max}} $
and corresponding simulation times for different values of h
s. The tag ‘NHD’ means No Hydraulic Damage. The points that are marked in the time plot with t → ∞ are those showing no crevasse propagation at all i.e.
$d_{\rm s}^{{\rm max}} $
and corresponding simulation times for different values of h
s. The tag ‘NHD’ means No Hydraulic Damage. The points that are marked in the time plot with t → ∞ are those showing no crevasse propagation at all i.e.
![]() $d_{\rm s}^{{\rm max}} /H = 0$
on the left plot.
$d_{\rm s}^{{\rm max}} /H = 0$
on the left plot.
The numerical Nye-zero depth is calculated as the depth of the material point (from the top surface) at which the horizontal tensile stress vanishes (σ xx = 0) and the values were recorded prior to damage propagation for all the simulations. The final crevasse depths retrieved from our damage simulations were always within 10% to those predicted by the Nye zero-stress model.
3.4. Effect of hydrodamage on surface and basal crevasse propagation
We next investigated the effect of hydrodamage on the simultaneous propagation of surface and basal crevasses. Unless the ocean water level is sufficiently high (h w/H > 0.8), surface crevasses always form in our simulation and it is not possible to have isolated basal crevasses without surface crevasses. This could be changed by setting a finite threshold for the largest principal stress as opposed to using a zero threshold as we did here. We find that, in accordance with the findings of Nick and others (Reference Nick, Van der Veen, Vieli and Benn2010) and Bassis and Walker (Reference Bassis and Walker2012), basal crevasses do not propagate unless they are water filled.
Through finite element simulation, we estimated surface and basal crevasse depths by varying the seawater height h
w/H = {0, 0.25, 0.6, 0.7, 0.8, 0.9} for two scenarios: (1) only basal crevasse is water filled and surface crevasse is dry, and (2) both surface and basal crevasses are water filled. The plots of normalized maximum (or final) crevasse depths (
![]() $d_{\rm s}^{{\rm max}} $
and
$d_{\rm s}^{{\rm max}} $
and
![]() $d_{\rm b}^{{\rm max}} $
) versus the normalized seawater height are shown in Figures 8, 9 for the two scenarios, respectively. In the case of a dry surface crevasse and water-filled basal crevasse (Fig. 8), our results indicate that the maximum total crevasse depth
$d_{\rm b}^{{\rm max}} $
) versus the normalized seawater height are shown in Figures 8, 9 for the two scenarios, respectively. In the case of a dry surface crevasse and water-filled basal crevasse (Fig. 8), our results indicate that the maximum total crevasse depth
![]() $(d_{\rm s}^{{\rm max}} + d_{\rm b}^{{\rm max}} )$
decreases as the seawater level increases until h
w/H = 0.8, but then increases as the seawater level further increases, h
w/H > 0.8. This is because the maximum surface crevasse depth decreases as seawater level increases, whereas, the maximum basal crevasse depth becomes significant only at high seawater levels, when the water pressure is sufficient to induce a tensile stress at the basal crack tips. Thus, our simulation results in Figure 8 are in good agreement with those published by Bassis and Walker (Reference Bassis and Walker2012). In Figures 8, 9, we plotted the time taken for the crevasses to reach the maximum (or final) depth as function of h
w/H. These results show that the crevasses propagation times are smallest for h
w/H = 0 and h
w/H = 0.9, indicating that the corresponding crevasse propagation rates are the largest for h
w/H = 0 and h
w/H = 0.9, which is attributed to the existence of higher tensile stresses at the surface and basal crack tips, respectively.
$(d_{\rm s}^{{\rm max}} + d_{\rm b}^{{\rm max}} )$
decreases as the seawater level increases until h
w/H = 0.8, but then increases as the seawater level further increases, h
w/H > 0.8. This is because the maximum surface crevasse depth decreases as seawater level increases, whereas, the maximum basal crevasse depth becomes significant only at high seawater levels, when the water pressure is sufficient to induce a tensile stress at the basal crack tips. Thus, our simulation results in Figure 8 are in good agreement with those published by Bassis and Walker (Reference Bassis and Walker2012). In Figures 8, 9, we plotted the time taken for the crevasses to reach the maximum (or final) depth as function of h
w/H. These results show that the crevasses propagation times are smallest for h
w/H = 0 and h
w/H = 0.9, indicating that the corresponding crevasse propagation rates are the largest for h
w/H = 0 and h
w/H = 0.9, which is attributed to the existence of higher tensile stresses at the surface and basal crack tips, respectively.

Fig. 8. Final crevasses' depths (
![]() $d_{\rm s}^{{\rm max}} $
for surface and
$d_{\rm s}^{{\rm max}} $
for surface and
![]() $d_{\rm b}^{{\rm max}} $
for basal) and corresponding simulation times under different values of near terminus water depth h
w; in these simulations, only the basal crevasses are water filled while the surface crevasses are dry. These results were simulated using B = 10−4 MPa−r
s−1.
$d_{\rm b}^{{\rm max}} $
for basal) and corresponding simulation times under different values of near terminus water depth h
w; in these simulations, only the basal crevasses are water filled while the surface crevasses are dry. These results were simulated using B = 10−4 MPa−r
s−1.

Fig. 9. Final crevasses' depths (
![]() $d_{\rm s}^{{\rm max}} $
for surface and
$d_{\rm s}^{{\rm max}} $
for surface and
![]() $d_{\rm b}^{{\rm max}} $
for basal) and corresponding simulation times under different values of side water pressure h
w; in these simulations, both surface and basal crevasses are water filled. These results were simulated using B = 10−4 MPa−r s−1. Note that final total crevasse depth is always larger when both basal and surfaces are water filled (compared blue dashed lines in Figures 8a and 9a), thus indicating a mutually positive effect.
$d_{\rm b}^{{\rm max}} $
for basal) and corresponding simulation times under different values of side water pressure h
w; in these simulations, both surface and basal crevasses are water filled. These results were simulated using B = 10−4 MPa−r s−1. Note that final total crevasse depth is always larger when both basal and surfaces are water filled (compared blue dashed lines in Figures 8a and 9a), thus indicating a mutually positive effect.
An important point to note is that surface and basal crevasses propagate to a greater depth (or height) when both are water filled (compare blue dashed lines in Figures 8a and 9a), thus indicating a mutually positive effect. To further investigate the effect of water-filled surface crevasses on basal crevasse propagation and vice-versa, we plot the temporal evolution of surface and basal crevasses in Figure 10 for water level h w/H = 0.25. The results in Figure 10 illustrate that the basal crevasse propagation is triggered when the surface crevasse approaches the bottom of the slab and alters the stress at the basal crevasse tip. The main conclusion of our study is consistent with previous studies: glaciers with dry surface crevasses are more stable than those with water-filled surface crevasses, and the situation worsens when the basal crevasses are water filled.

Fig. 10. Damage propagation for the case of h w/H = 0.25 from Figure 9 (surface and basal crevasses are water filled). The top plot shows crevasses propagation with time and the following are snapshots of damage contours at different time steps. These results were simulated using B = 10−4 MPa−r s−1.
In this study, we did not exclusively investigate conditions that enable the propagation of only a basal crevasse without a surface crevasse. Because we assume that glacier ice has zero tensile strength, surface crevasses will always form while simulating an extending glacier and so it is not possible to have isolated basal crevasses without surface crevasses. However, the model can account for the tensile strength for ice by specifying a stress threshold for damage initiation (Pralong and Funk, Reference Pralong and Funk2005), which disables the formation of surface crevasses at very low deformation rates. Similarly, including a sliding law instead of a free-slip boundary condition would quantitatively alter our simulation results. Nonetheless, the hydraulic damage methodology we have developed is directly applicable to more complex geometries, boundary conditions and rheologies.
4. CONCLUSION
In this paper, we demonstrated the viability of a continuum damage approach to model the propagation of water-filled crevasses. Using the poromechanics concept of effective solid stress, a viscoelastic damage model is developed to simulate hydraulic fracture of glacier ice, within a Lagrangian finite element framework. The advantages of using the proposed damage mechanics approach over the LEFM approach are: (1) the incorporation of a viscoelastic constitutive law to model the time dependent mechanical behavior of ice, (2) the elimination of adaptive remeshing or mesh moving procedures to model crevasse propagation. Although the model is developed for the small strain case assuming additive decomposition of strain, it can be extended to the finite strain case assuming multiplicative decomposition of the deformation gradient tensor (Keller and Hutter, Reference Keller and Hutter2014b).
Several numerical examples and sensitivity studies are considered to analyze the effects of water-filled surface and basal crevasses on the process of iceberg calving from idealized grounded glaciers. The finite element simulations considered different cases of ocean water levels, presence of surface lakes and variable piezometric water levels at basal crevasses. Several conclusions about the crevasse propagation could be drawn from the numerical results. The water-filled crevasses tend to propagate further and faster than dry ones. Basal crevasses require a sufficiently high water pressure to start propagating, which is in accordance with the findings of previous studies. However, in contrast to studies that ignore the feedback between surface and basal crevasses, water-filled surface and basal crevasses alter the stress state and interactively stimulate crevasse propagation deeper into the glacier, thus, speeding up the fracture process.
ACKNOWLEDGEMENTS
The authors are grateful for the funding support provided by the National Science Foundation, Polar Programs division, Grant # PLR-1341472, PLR-1341568 and PLR-1341428. The authors would like to thank scientific editor, Ralf Greve and two reviewers, Arne Keller and an anonymous reviewer, for valuable and critical comments that helped improve the manuscript.
Appendix A SIMPLIFIED UNIAXIAL DERIVATION OF VISCOELASTIC DAMAGE MODEL WITH PORE PRESSURE
In this Appendix, we illustrate that the viscoelastic damage model used to describe a damaged Maxwell viscoelastic material under a uniaxial stress state, thus, proving that it is suitable for representing the non-Newtonian fluid like behavior of glacial ice with damage evolution. Assuming the uniaxial macroscopic loading in the real stress state, the full stress tensor σ
kl and the deviatoric stress tensor
![]() $\sigma _{{\rm kl}}^{{\rm dev}} $
become
$\sigma _{{\rm kl}}^{{\rm dev}} $
become
 $$\eqalign{[{\sigma _{{\rm kl}}}] &= \left[ {\matrix{ {{\sigma _{11}}} & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}} \right],\cr \hskip-2pt\left[ {\sigma _{{\rm kl}}^{{\rm dev}}} \right] &= \left[ {\matrix{ {\displaystyle{2 \over 3}{\sigma _{11}}} & 0 & 0 \cr 0 & { - \displaystyle{1 \over 3}{\sigma _{11}}} & 0 \cr 0 & 0 & { - \displaystyle{1 \over 3}{\sigma _{11}}} \cr}} \right],}$$
$$\eqalign{[{\sigma _{{\rm kl}}}] &= \left[ {\matrix{ {{\sigma _{11}}} & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}} \right],\cr \hskip-2pt\left[ {\sigma _{{\rm kl}}^{{\rm dev}}} \right] &= \left[ {\matrix{ {\displaystyle{2 \over 3}{\sigma _{11}}} & 0 & 0 \cr 0 & { - \displaystyle{1 \over 3}{\sigma _{11}}} & 0 \cr 0 & 0 & { - \displaystyle{1 \over 3}{\sigma _{11}}} \cr}} \right],}$$
hence, the elastic strain component
![]() ${\epsilon} _{{\rm 11}}^{\rm e} $
for undamaged ice is given by
${\epsilon} _{{\rm 11}}^{\rm e} $
for undamaged ice is given by
where E is the Young's modulus of undamaged ice and the viscous strain rate in Eqn (5) can be written in the form
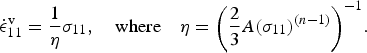 $${\dot \epsilon} _{{\rm 11}}^{\rm v} = \displaystyle{1 \over \eta} {\sigma _{11}},\quad {\rm where}\quad \eta = {\left( {\displaystyle{2 \over 3}A{{({\sigma _{11}})}^{(n - 1)}}} \right)^{ - 1}}.$$
$${\dot \epsilon} _{{\rm 11}}^{\rm v} = \displaystyle{1 \over \eta} {\sigma _{11}},\quad {\rm where}\quad \eta = {\left( {\displaystyle{2 \over 3}A{{({\sigma _{11}})}^{(n - 1)}}} \right)^{ - 1}}.$$
Differentiating the elastic component with respect to time and assuming small elastic deformations, we can add the elastic and viscous components to write the total strain rate as
The above equation represents a 1-D Maxwell viscoelastic element that can be represented by a spring with stiffness E and a dashpot with viscosity η connected in series.
Including the effect of damage in the spring and dashpot under dry conditions, we can write the elastic and viscous strain rates as
The total strain rate can now be expressed as
where the ‘damaged’ modulus E
d = (1 − D)E and a dashpot with ‘damaged’ viscosity η
d = (1 − D)
n
η. Next, recalling Eqn (13) upon including the effect of pore pressure P
h under wet conditions we find the only non-zero component of the stress tensor is
![]() ${\sigma _{11}} = (1 - D)E{\epsilon} _{{\rm 11}}^{\rm e} - D{P^{\rm h}}$
. Rewriting the above equation and neglecting the contribution of damage rate
${\sigma _{11}} = (1 - D)E{\epsilon} _{{\rm 11}}^{\rm e} - D{P^{\rm h}}$
. Rewriting the above equation and neglecting the contribution of damage rate
![]() $\dot D$
(small damage rate assumption), the elastic strain rate then becomes
$\dot D$
(small damage rate assumption), the elastic strain rate then becomes
and using Eqn (14), the effective solid stress becomes
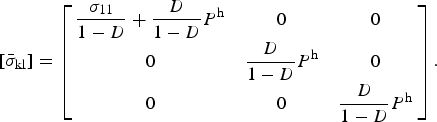 $$[{\bar \sigma _{{\rm kl}}}] = \left[ {\matrix{ {\displaystyle{{{\sigma _{11}}} \over {1 - D}} + \displaystyle{D \over {1 - D}}{P^{\rm h}}} & 0 & 0 \cr 0 & {\displaystyle{D \over {1 - D}}{P^{\rm h}}} & 0 \cr 0 & 0 & {\displaystyle{D \over {1 - D}}{P^{\rm h}}} \cr}} \right].$$
$$[{\bar \sigma _{{\rm kl}}}] = \left[ {\matrix{ {\displaystyle{{{\sigma _{11}}} \over {1 - D}} + \displaystyle{D \over {1 - D}}{P^{\rm h}}} & 0 & 0 \cr 0 & {\displaystyle{D \over {1 - D}}{P^{\rm h}}} & 0 \cr 0 & 0 & {\displaystyle{D \over {1 - D}}{P^{\rm h}}} \cr}} \right].$$
The inclusion of pore-pressure leads to a 3-D effective stress state. Because the deviatoric stress is unaffected by an additional hydrostatic stress, the viscous strain rate
![]() ${\dot \epsilon} _{{\rm 11}}^{\rm v} $
is unaffected by pore-pressure P
h and so the total strain rate becomes
${\dot \epsilon} _{{\rm 11}}^{\rm v} $
is unaffected by pore-pressure P
h and so the total strain rate becomes
The damage evolution rate for ice under wet conditions remains
but the Hayhurst equivalent stress χ can now be written in the form
 $$\eqalign{&\chi = \cr & \hskip-5pt\left(\hskip-2pt {\matrix{ {\alpha \;\displaystyle{{{\sigma _{11}} + D{P^{\rm h}}} \over {1 - D}} + \beta \displaystyle{{{\sigma _{11}}} \over {1 - D}} \hskip-0.5pt+\hskip-1pt (1 - \alpha - \beta )\displaystyle{{{\sigma _{11}} + 3D{P^{\rm h}}} \over {1 - D}},}\hskip-2pt & {{\rm if}\quad \displaystyle{{{\sigma _{11}} + D{P^{\rm h}}} \over {1 - D}} \gt 0,} \cr {0,} & {{\rm if}\quad \displaystyle{{{\sigma _{11}} + D{P^{\rm h}}} \over {1 - D}} \le 0,} \cr}} \right.}$$
$$\eqalign{&\chi = \cr & \hskip-5pt\left(\hskip-2pt {\matrix{ {\alpha \;\displaystyle{{{\sigma _{11}} + D{P^{\rm h}}} \over {1 - D}} + \beta \displaystyle{{{\sigma _{11}}} \over {1 - D}} \hskip-0.5pt+\hskip-1pt (1 - \alpha - \beta )\displaystyle{{{\sigma _{11}} + 3D{P^{\rm h}}} \over {1 - D}},}\hskip-2pt & {{\rm if}\quad \displaystyle{{{\sigma _{11}} + D{P^{\rm h}}} \over {1 - D}} \gt 0,} \cr {0,} & {{\rm if}\quad \displaystyle{{{\sigma _{11}} + D{P^{\rm h}}} \over {1 - D}} \le 0,} \cr}} \right.}$$
from which it is apparent that pore pressure increases χ and allows damage to initiate under conditions experiencing a lower tensile stress state.
Appendix B PURELY VISCOUS UNIAXIAL MODEL
In the absence of elastic strains, the proposed model can be proven to behave as a viscous material. The purely viscous uniaxial model corresponds to taking the limit E → ∞ in Equation (A10). This leads to the relation
or, more intuitively
The only place pore pressure enters the model now is through the damage metric defined in Eqn (A12).












