Modelling ice-divide dynamics by perturbation methods

Abstract

Two-dimensional, isothermal, non-stationary, cold-glacier dynamics are analysed by perturbation methods, when the ice creep is described by Glen’s flow law. This approach allows us in model the ice-divide dynamics separately from that of the glacier and to pose a simplified problem for the ice divide. To order of the glacier-aspect ratio, all unknown characteristics near the ice divide can be searched for in an infinite layer with parallel boundaries, whose thickness coincides with that found by the shallow-ice approximation. The problem for the ice divide is stationary and does not depend on the ice and glacier characteristics, such as a flow-law constant, ice thickness and accumulation rate. At the ice divide, the ice upper surface curvature is finite and the shallow-ice approximation is inadequate.

1. Introduction

The ice divide of a glacier is characterized by the absence of ice horizontal motion. This simplifies the ice-age dating necessary for palaeoclimatic reconstructions. At the same time, an ice divide is a special region, where for Glen’s flow law, the shallow-ice approximation (Morland and Johnson. 1980; Hutter, 1983) breaks down and the full system of Stokes’ equations is to be solved (Dahl-Jensen, 1989; Fowler, 1992).

Whereas there are many works devoted to the numerical solution of the problem (Raymond, 1983; Dahl-Jensen, 1989; Szidarovski and others, 1989), analytical treatment has brought out difficulties associated with assuming simplifications, which can be inadequate near an ice divide Reeh, 1988). Morland and Johnson (1980) have shown that the shallow-ice approximation gives an infinite upper-surface curvature for the power flow-law exponent n > 1 when there is no slip at the bed. Assuming sliding with the “Weertman-type” law gives finite surface curvature for n = 1, n = 2, n ≥ 3 and m ≤ 1, where m is the sliding-law exponent. Hindmarsh (personal communication) has found that the inclusion of iongitudinal stresses in the model gives finite curvature at the ice divide. Fowler (1992) sketched an asymptotic analysis, which showed that neither the vertical shear stress nor the longitudinal one can be neglected at an ice divide in the isothermal case.

Some characteristics of ice flow near an ice divide have been shown by a numerical solution of the problem. Raymond (1983) has pointed out that derived velocities are insensitive to changes of the ice upper-surface profile. His results for ice velocities also show that the shallow-ice approximation is valid in an ice divide for a Newtonian fluid and is not when Glen’s flow law is used. Dahl-Jensen (1989) has demonstrated numerically that the length of the ice-divide singular zone is of an order of an ice thickness there.

Difficulties in modelling the ice-divide dynamics by numerical techniques are caused by the small ratio of the ice-divide length to that of the glacier (it is of order 0.01 or less),Therefore, the ice motion at the ice divide is modelled separately from the ice motion in the glacier (Raymond, 1983; Dahl-Jensen, 1989). Although efficient numerical techniques have been used and tested by many authors (Raymond, 1983; Dahl-Jensen, 1989; Szidarovski and others, 1989), the question of posing the problem at the ice divide is still open. What region should be considered in modelling the ice-divide dynamics separately from the glacier motion?. What boundary conditions should be used? How should one model the non-steady state? And what is the interaction between the ice divide and the glacier?

Despite the fact that the temperature distribution exerts a strong influence on the values of the ice velocities (Morland and Smith, 1983; Raymond, 1983; Fowler, 1992), it is also necessary to study the isothermal case. Such an analysis can demonstrate the main structure, which will persist in non-isothermal ice motion.

In this work, we study two-dimensiona;, non-steady, isothermal, cold - glacier dynamics by perturbation methods, when the ice creep is described by Glen’s flow law. The main purpose of this study is to determine simplifications admissible in the vicinity of a symmetric ice divide and to address the question: what problem should be solved to model the ice-divide dynamics in the must simplified way? The auxiliary assumptions arc a no-slip condition at the bed (Fowler, 1981), regularity of the bed profile at the divide (i.e. zеrо first-longitudinal derivative) and absence of mass flux at the bed. We also neglect the bed local fluctuations, whose amplitude is assumed to be small in contrast with the ice thickness. Existence ofa weak boundary layer near the glacier surface, which does not change the velocity distribution Johnson and McMeeking, 1984), is not taken into account in this study.

Following the theory of perturbation methods (Cole, 1968), we model the ice-divide dynamics by the near-field solution, whereas the shallow-ice approximation gives us the Far-field problem. A similar approach has been applied by Johnson and McMeeking (1984) in modeling0 the boundary layer near the ice-free surface.

2. Equations

2.1 Setting the problem

Considering a two-dimensional glacier, let us place the origin of a rectangular righthanded coordinate system (z axis is directed vertically upwards) at the bed at the ice divide. Let square brackets on any quantity define its scale magnitude in the glacier. Let g be the acceleration due to gravity and ρ_i be the ice density. Table 1 shows the notation in the original coordinate system (variable) and in that sealed for the glacier : (scaled) by scales (Salamatin and Mazo, 1984). This table also shows the notation of the variables in the coordinate system for the ice divide (divide) (see section 4: near-field solution for the ice divide). We shall also use the notation for the partial derivative ℓ′ = ∂ℓ/∂x.

Table I. Notation

Ice flow, assuming incompressibility of the ice, can be described by the following Stokes equations:

(1)

The above set of equations must be completed bv the following boundary conditions.

The glacier upper surface z= l(x) is stress-free and the kinematic boundary condition is used to determine its profile:

(2)

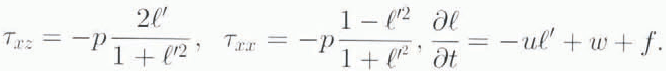
The no-slip condition at the bed z = z₀(x) may be assumed for the cold Antarctic ice sheet, where sliding is negligible (Fowler, 1981):

(3)

At the ice divide x = 0, the mass flux is zero and the fluid flow is symmetric:

(4)

At the glacier terminus x_m it is sufficient to impose the value of the glacier-surface elevation:

(5)

For example, l_m can be zеrо for a grounded glacier or can be derived from the condition of hydrostatic equilibrium of the ice in the water for a marine glacier (Chugunov and Wilchinsky, 1996).

2.2 Non-dimensionalization

Far from the ice divide, the ice flow is described by the shallow-ice approximation (Morland and Johnson, 1980; Hutter, 1983), where the shear stress is much larger than the longitudinal stress. Let us non-dimensionalize the governing equations with the scales found by Salamatin and Mazo (1984) (see also Fowler, 1992) on the basis of similarity theory (Table 1). Then, dimensionless system of Equations (1)–(5) can be converted to the following problem for the stream function and the unknown upper-surface elevation L (capital letters denote the dimensionless variables) (Chugunov and Wilchinsky, in press: for the case of a Newtonian fluid see Chugunov and Wilchinsky, 1996): Stream function:

(6)

Upper surface Z = L(X,T):

(7)

bed Ζ = Z₀(X) :

(8)

Ice divide X = 0:

(9)

Equation For the surface profile L(X, T):

(10)

Excess pressure:

(11)

Margin:

(12)

Equations (6) and (7) are derived from Equations (1) and (2) via exclusion of the function p . Equation (10) is a result of successive integration of the first Equation (1) from z to z₀ With respect to z and then from x to 0 with respect to x . The constant C is to be determined from Equation (12).

Most cold glaciers are characterized by a value of the parameter ∈ « 1. This parameter is the typical ice-surface slope and reflects conditions of the glacier existence, such as the glacier lengths, the accumulation rate and the ice viscosity.

3. Far-Field Solution for the Glacier

We seek an expansion for the stream function and the glacier surface ψ^(g) , L^(g) in the far field as an asymptotic series in ∈ :

Then, from Equations (6)–(10), we derive the solution describing Poiseuille flow (Salamatin and Mazo, 1984): Stream function:

Surface elevation:

(13)

Considering the found solution as the distance from the ice divide X → 0, we obtain: Stream function:

(14)

Surface elevation:

Equations (13) allow us to determine the upper-surface profile of the glacier far from the ice divide. It should be noted that these equations describe the upper-surface profile with infinite Curvature at the ice divide (Morland and Johnson, 1980; Hindmarsh, personal communication), where the solution breaks down. However, it is not true for stream function itself. Because ψ → 0 as X → 0 and all the boundary conditions are satisfied, we have O(∈), ∀X. The solution breaks down at least for the vertical velocity –∂ψ/∂X, which is finite at the ice divide. Therefore, it is necessary to examine the problem X → 0 (Fowler, 1992) to find the solution at the ice divide.

4 Near-Field Solution for the Ice Divide

4.1 Equations

It follows from Equations (6) and (14) that the shallow-ice approximation (shear stresses dominate longitudinal stresses) breaks down when X ~ ∈ , because ∂² ψ/∂Z ² ~ ∈ in this case (Fowler, 1992), i.e. the shear and longitudinal stresses are equally significant at the ice divide. In order to analyse the problem in the vicinity of the ice divide, we use local expansion of the solution.

Denoting the ice thickness at the ice divide in the scales of the glacier by L_d , let us introduce the near-field coordinates and variables:

Rewriting Equations (6)–(12) in the new variables and neglecting local bed fluctuations, we derive (we also assume Z’₀ (0) = 0 because of symmetry):

(15)

Surface у = χ(ξ) :

(16)

Bed

(17)

Divide ξ = 0:

(18)

Equations (15)–(18) define the stream function ψ . For the upper-surface profile χ it follows from Equations (10)–(12) that we have the following equation:

(19)

It was used in deriving Equations (17) that near the ice divide we have the bed profile Z₀(X) = O(X²) = O(∈²).

From the boundary conditions for the stream function ψ , it can be seen that ψ ∼ ∈ . Therefore, to analyse the problem, let us introduce the normalized stream function Ψ = ψ/∈L _d(F(0) – dL _d/dT) to have all the derivatives of order 1. Then, the set of Equations (15)–(19) takes the following form:

(20)

Surface y = χ(ξ):

(21)

Bed y = O(∈₂) :

(22)

Divide ξ = 0 :

(23)

Upper-surface elevation χ :

(24)

4.2 Expansion in ∈

It should be noted that at the ice divide all the unknown functions depend on ∈ and ∈^1+1/n . Therefore, we seek the solution of Equations (20)–(24) as an asymptotic series ∈ and ∈^1+1/n : Stream function

bed

Surface

Unknown constant

For the leading-order terms and for the first-order correction χ1 we have the following set of equations, where the stream function ψ₀ does not depend on the time and the glacier characteristics (glacier length, accumulation rate, flow-law constant, ice thickness):

(25)

Surface у = 1 :

(26)

Bed y = 0:

(27)

Divide ξ = 0:

(28)

Surface elevation

(29)

(30)

Deriving Equations (29) and (30), in order to determine A₀ and A₂ . we use the expanded initial condition for the surface elevation χ : χ₀ (0) = 1; χ₁ (0) = 0.

The set of Equations (25)–(30) describes the ice flow in the vicinity of the ice divide. The problem for the stream function ψ₀ does not depend on the glacier characteristics except for the flow-law exponent n. for n = 1, formula (14), describing the shallow-ice approximation, satisfies Equations (25)–(28). To order O(∈^1+1/n),we can neglect the ice upper-surface slope. However, because the leading-order term for the ice-surface elevation is a constant, the solution fot the glacier-surface elevation matched to order O(∈^1+1/n) coincides with the far-field one, Equation (13), and still has infinite curvature at the ice divide. Therefore, it is necessary to find the upper-surface elevation χ to higher order of accuracy to ascertain that the curvature is finite. The ice thickness L_d is to be determined by matching the far-lield solution and the near-field one.

After matching, the near- and the far-field solutions to order of ∈^2+1/n , the solution χ for the upper-surface elevation has finite curvature and can be written in the following (form see Appendix): Surface

Icе thickness at the ice divide

It should be noted that, although the upper-surface elevation χ has finite curvature, it has an infinite third derivative: Again, the matched to order O(∈) stream function has the first continuous derivatives (i.e. velocities), whereas the second derivative with regard to X is infinite at the ice divide due to infinite curvature of the outer upper surface. This can be eliminated by finding the solution to higher order of accuracy. To avoid this problem, near the ice divide, only the near-field solution should be used for determina¬tion of all the characteristics, whereas in the glacier ihe shallow-ice approximation is adequate. It is also seen that to order O(∈^1+1/n) the ice thickness at the ice divide coincides with that found by the shallow-ice approximation (far-field solution).

Physically, the near-field problem for the stream function describing the ice-divide dynamics is equivalent to the full system of Stokes’ equations in an infinite layer with parallel boundaries, when the vertical velocity at the ice surface (f – ∂ℓ/∂t) does not depend on the horizontal coordinate. By scaling the spacial coordinates and the velocities on the layer thickness and the value of vertical velocity at the surface, respectively, which are found by the shallow-ice approximation, the Stokes’ problem is transformed to a steady form. For the isothermal case considered here, the Steady Stokes’ problem is to be solved only once. The non-steady solution is derived only by inverse transformation of the variables.

Results for the radial case can be derived by the same procedure as for the linear one (paper in preparation). In so doing, one can find that all derived estimates as to the upper surface slope and the ice thickness at the ice divide do not change.

It is clear that, for the non-isothermal state, estimates as to the upper surface slope and the ice thickness will not also change. However, the problem for the ice divide will not be steady due to the temperature distribution.

4.3 Numerical analysis

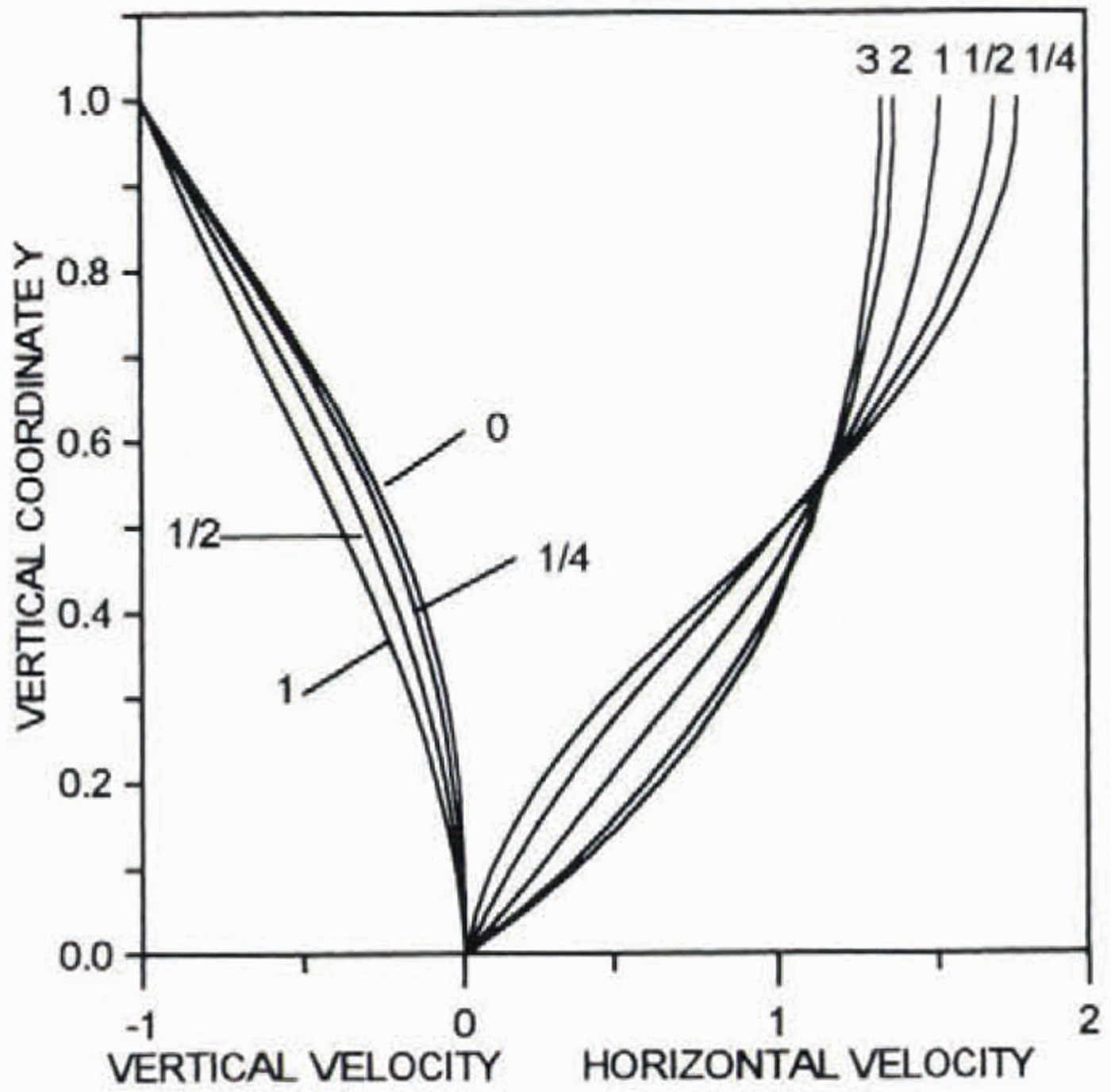
Problems (25)–(28) for the stream function ψ₀ was solved numerically for the flow-law exponent n = 3 and with discretization length equal to 0.05. The results are similar to those derived by Dahl-Jensen (1989) for non-isothermal ice flow. Figure 1 presents profiles of the vertical velocity (–∂Ψ₀/∂ξ) and the normalized horizontal (∂Ψ₀/∂y)/ξ. The results are shown for different ξ (distance from the ice divide). In the vicinity of the ice divide, the profile of the horizontal velocity has an inflection. The far-field solution for the vertical velocity is valid at a distance from the ice divide of about one ice thickness, whereas for the horizontal velocity this distance is about six ice thicknesses (with sufficient accuracy it can be taken as three ice thicknesses).

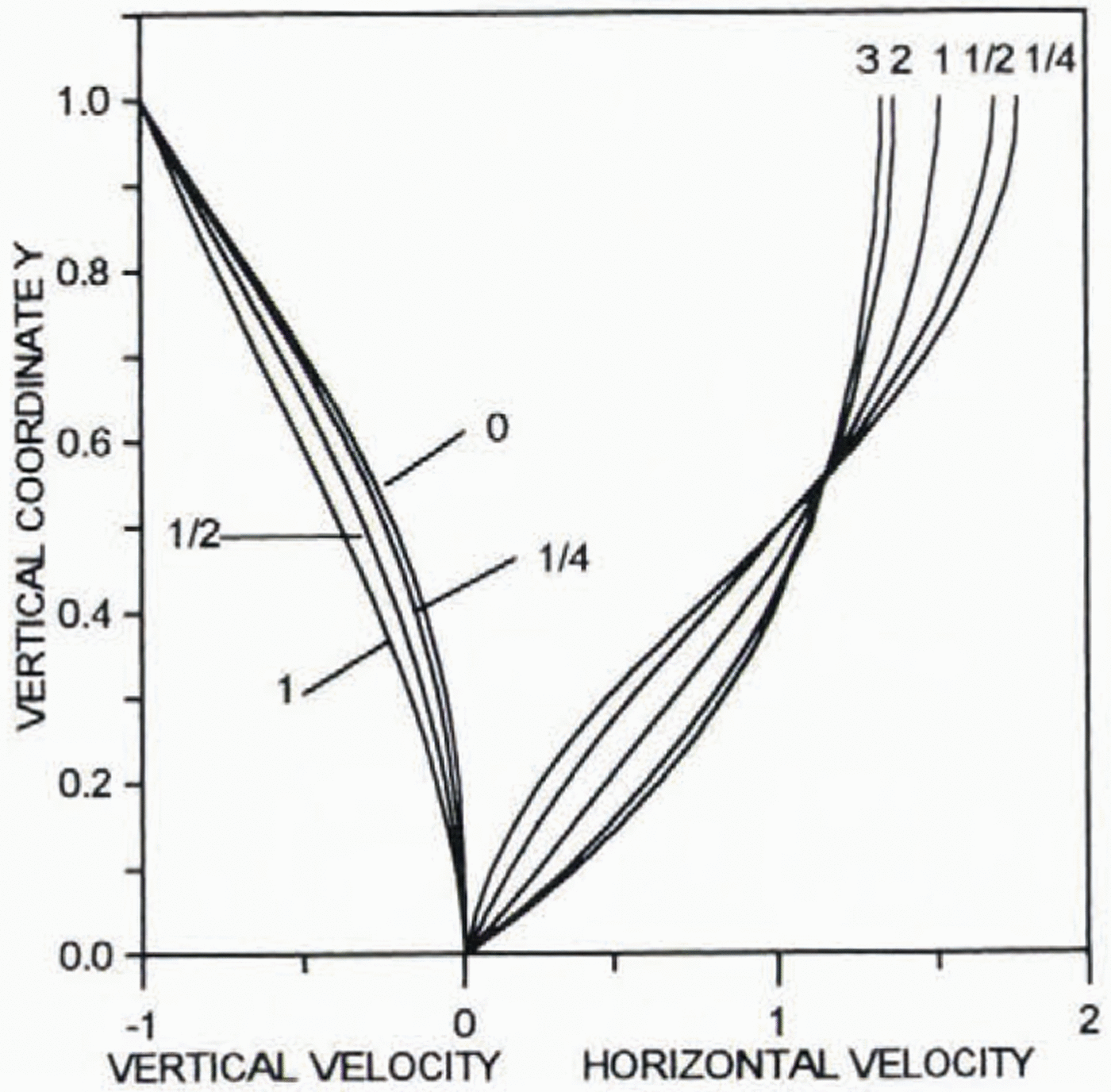
Fig. 1. Profiles of the dimensionless normalized horizontal (∂Ψ₀/∂y)/ξ and vertical (–∂Ψ₀/∂ξ) velocities. Numbers

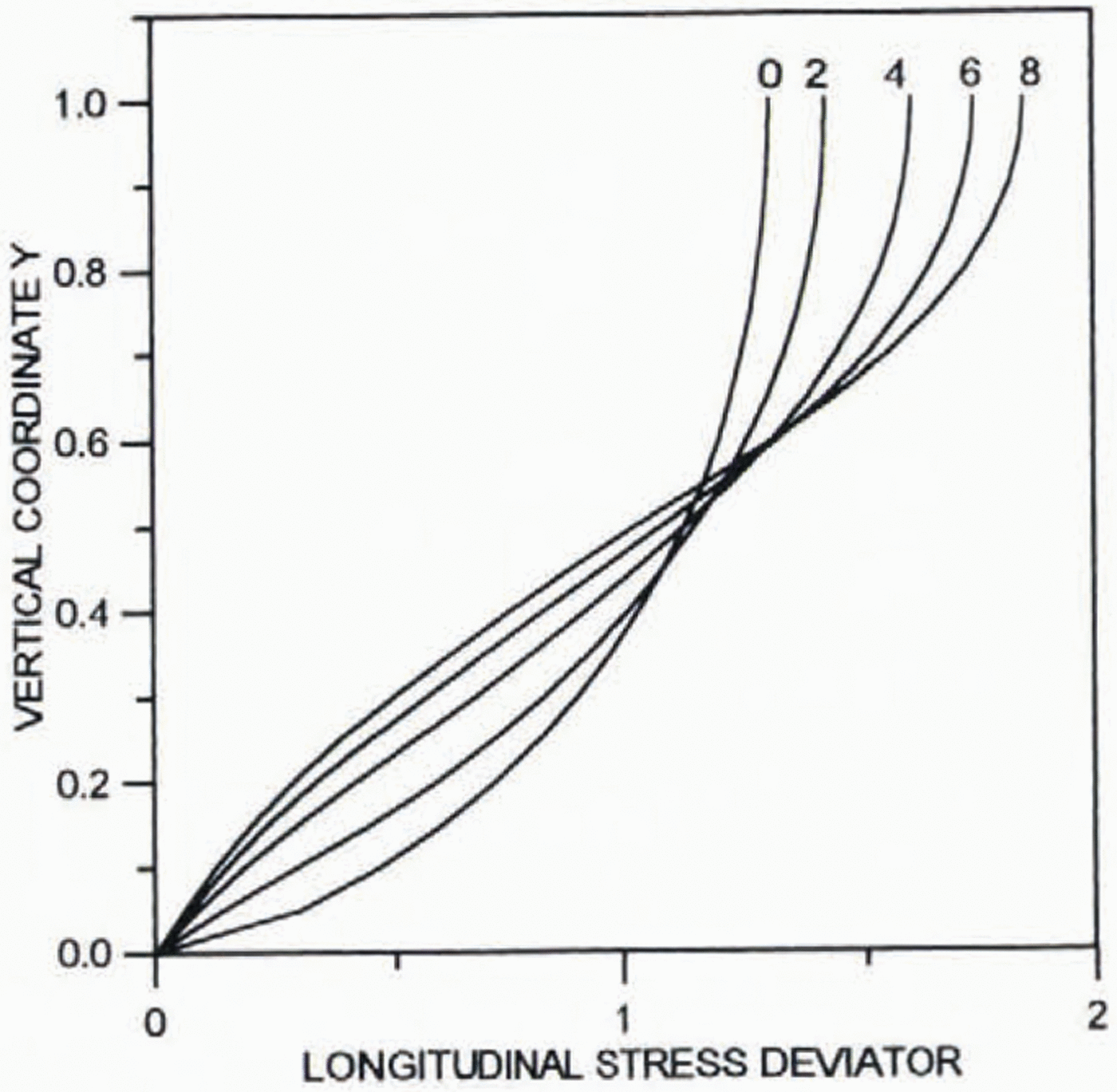
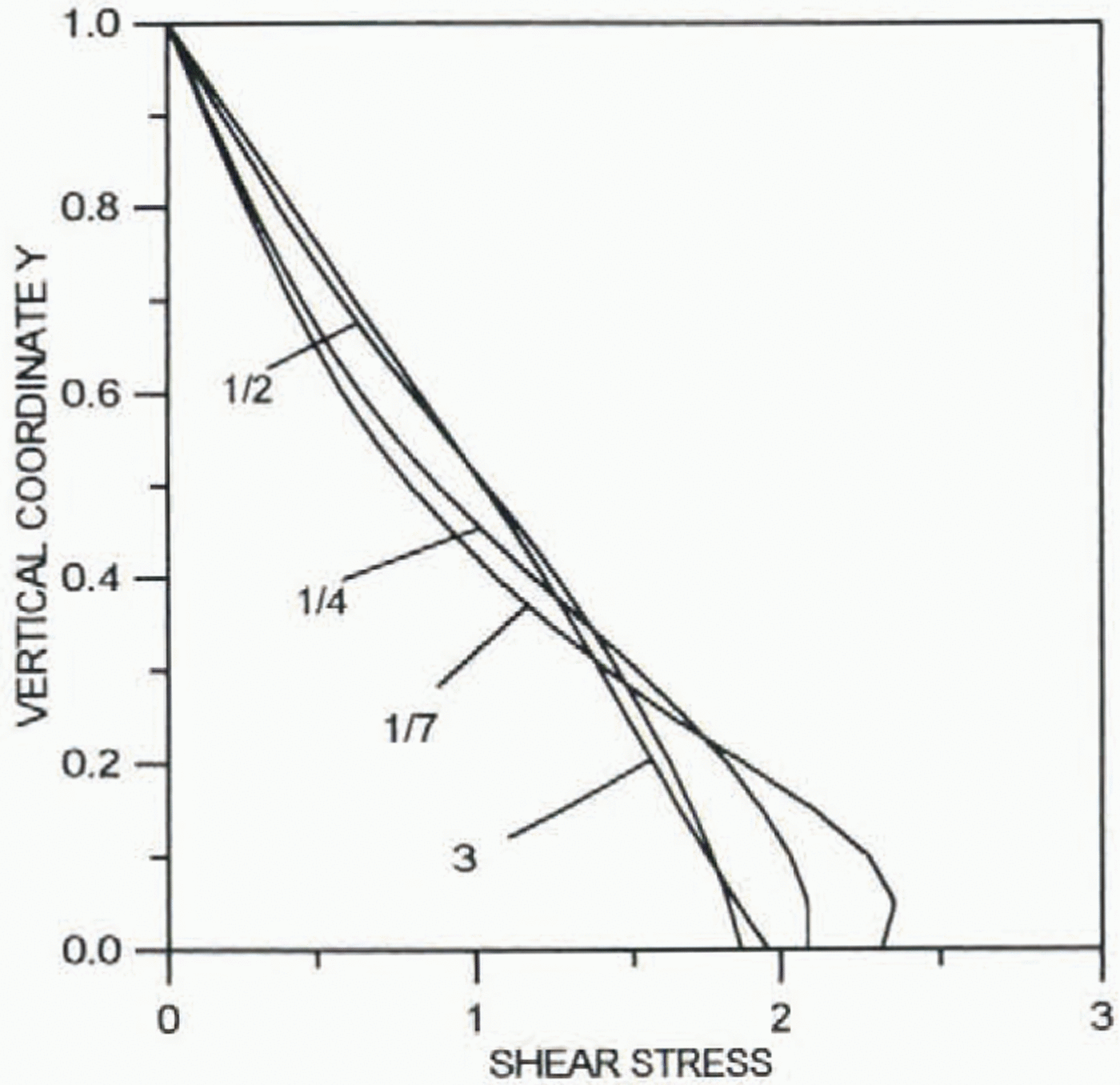
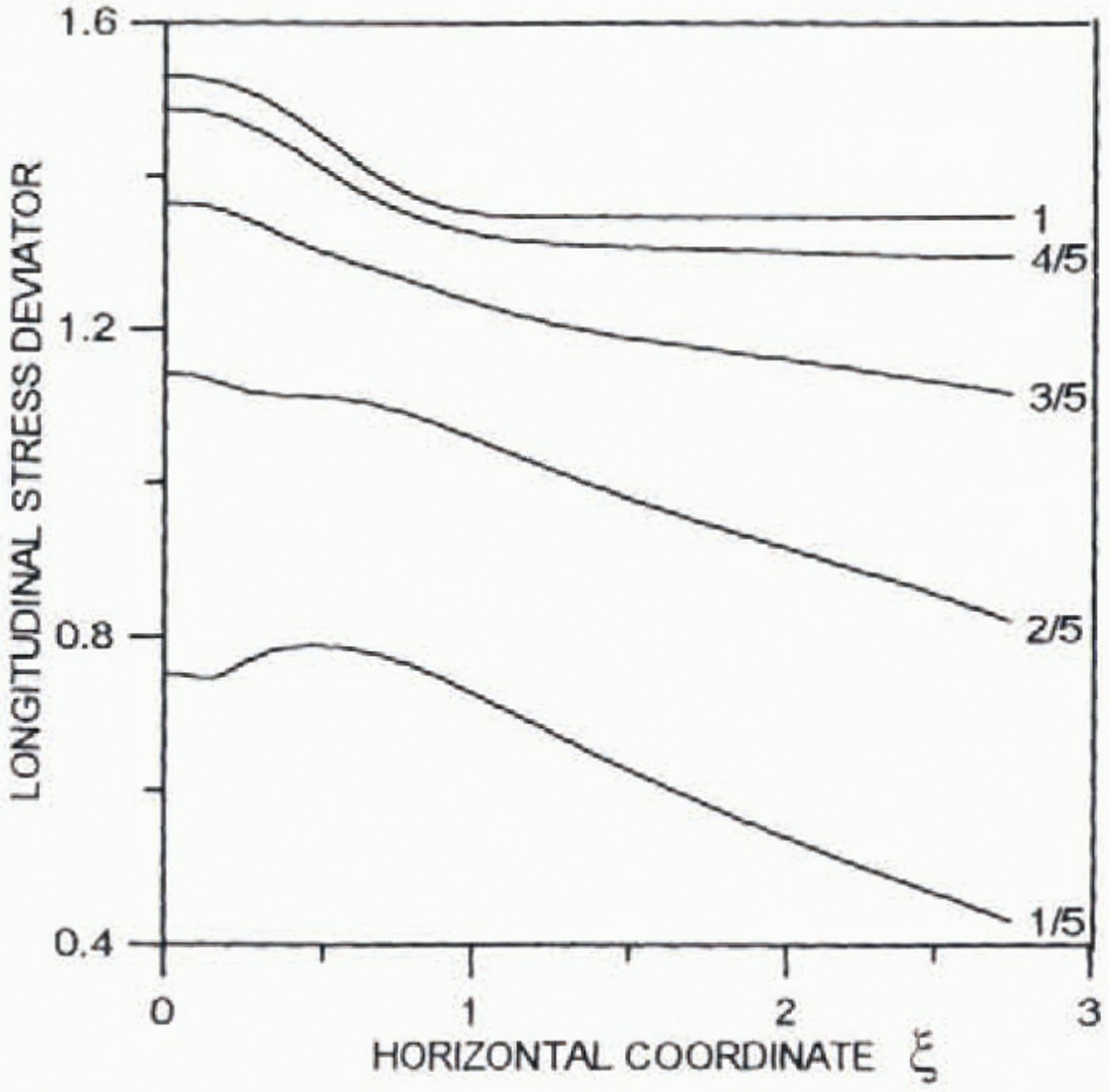
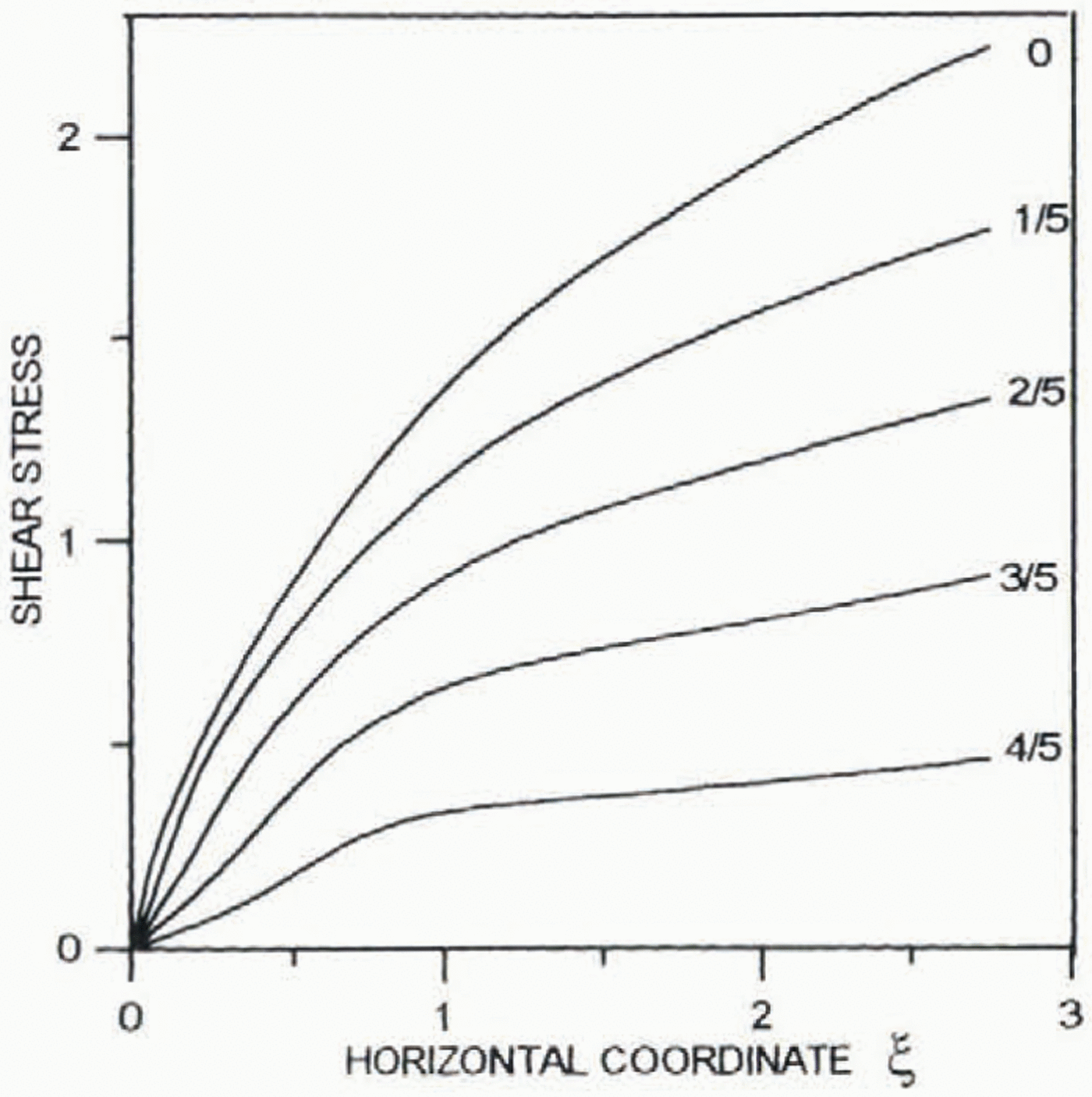
Figures 2 and 3 present results of calculations for the normalized longitudinal deviatoric stress 2μ∂²Ψ₀/∂ξ∂y and shear stress μ ₀(∂²Ψ₀/∂y ²–∂²Ψ₀/∂²ξ², respectively. All the stresses are normalized by their average values. The far-field solution for the shear stress is valid at a distance from the ice divide of about two ice thicknesses.

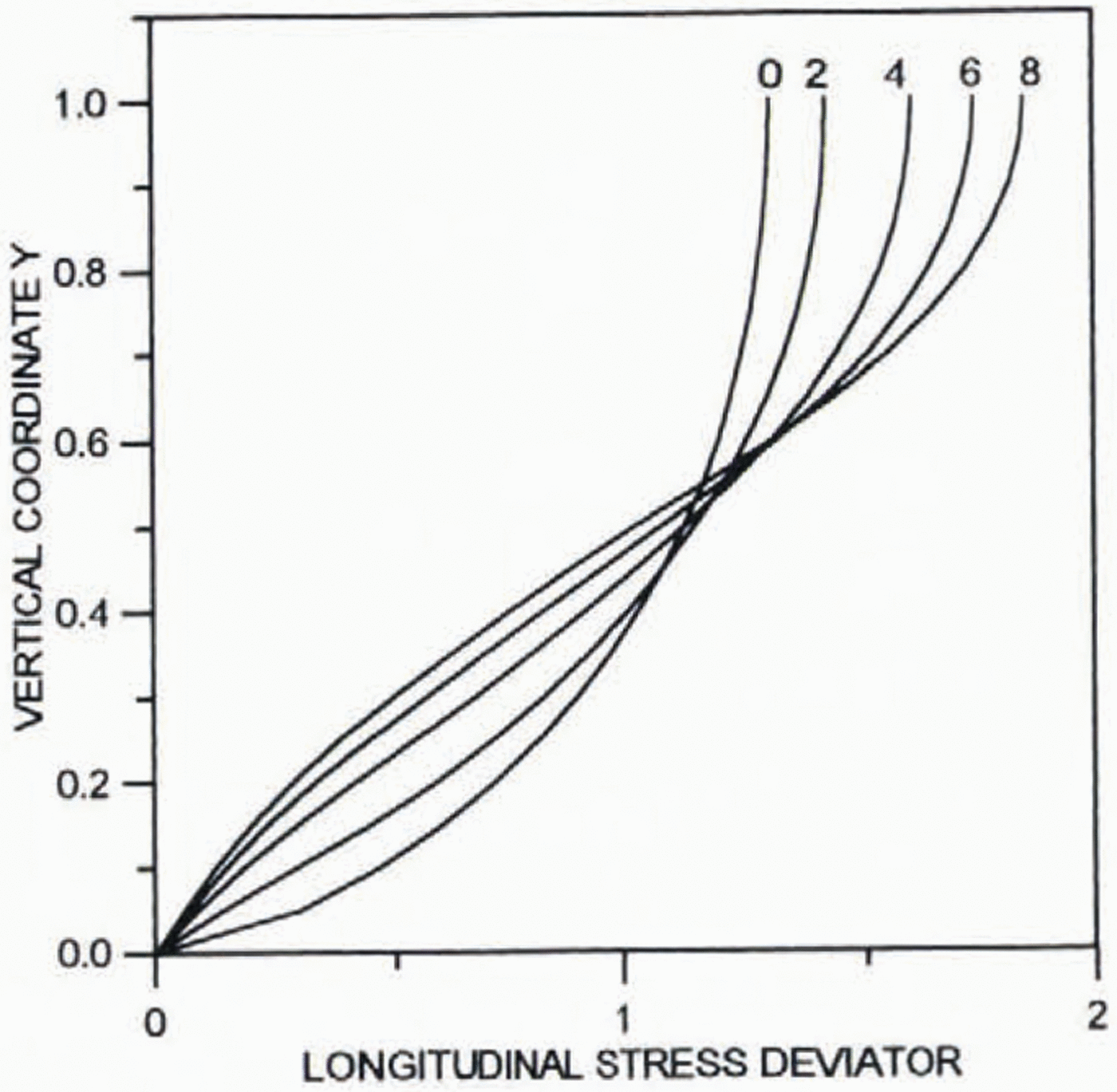
Fig. 2. Profiles of the dimensionless normalized longitudinal deviatoric stress 2μ ₀∂²Ψ₀/∂ξ∂y for different distances from the ice divide.

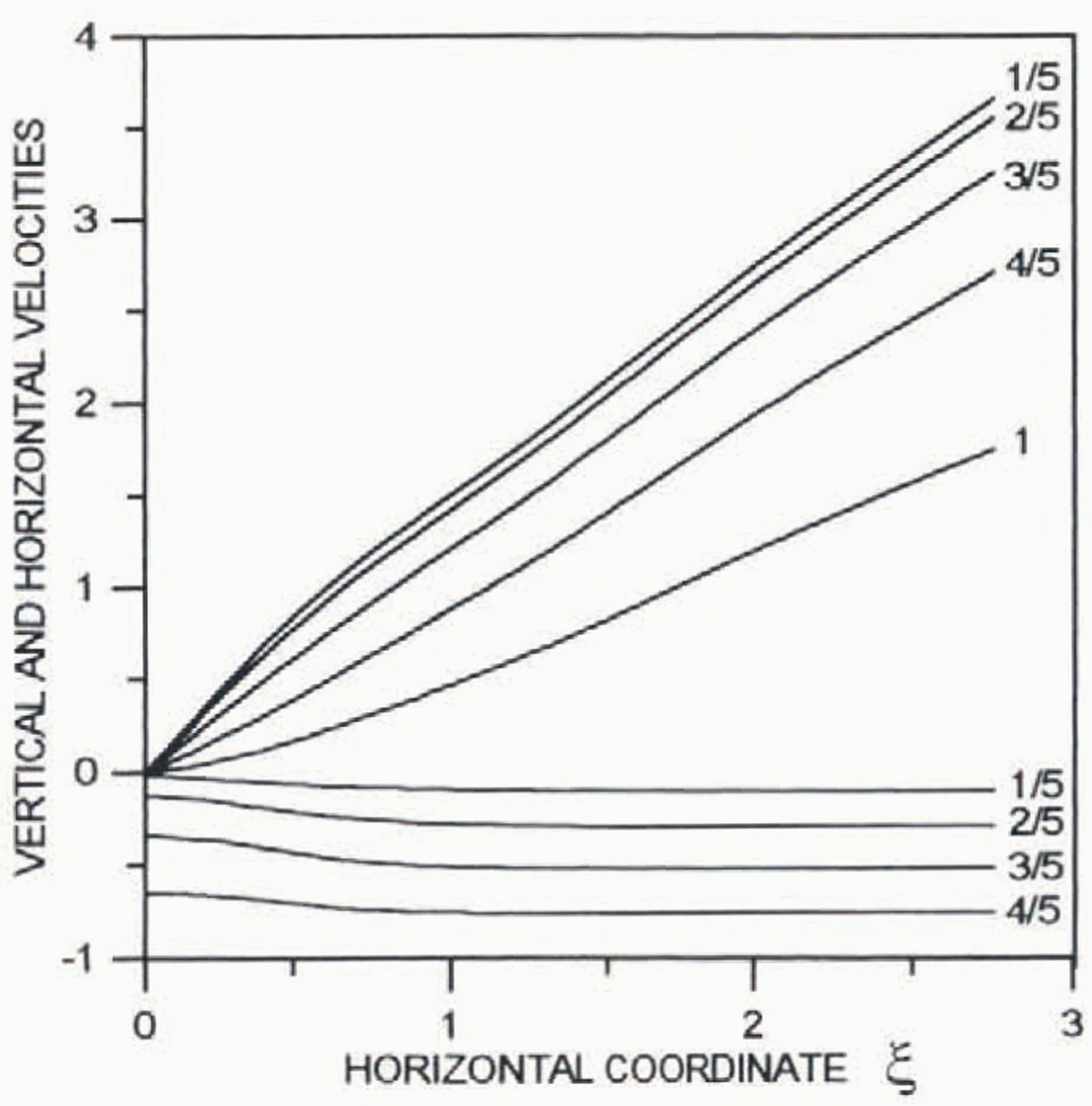
Fig. 3. Profiles of the dimensionless normalized shear stress 2μ ₀∂²Ψ₀/∂y ² – ∂²ξ₀∂ξ².

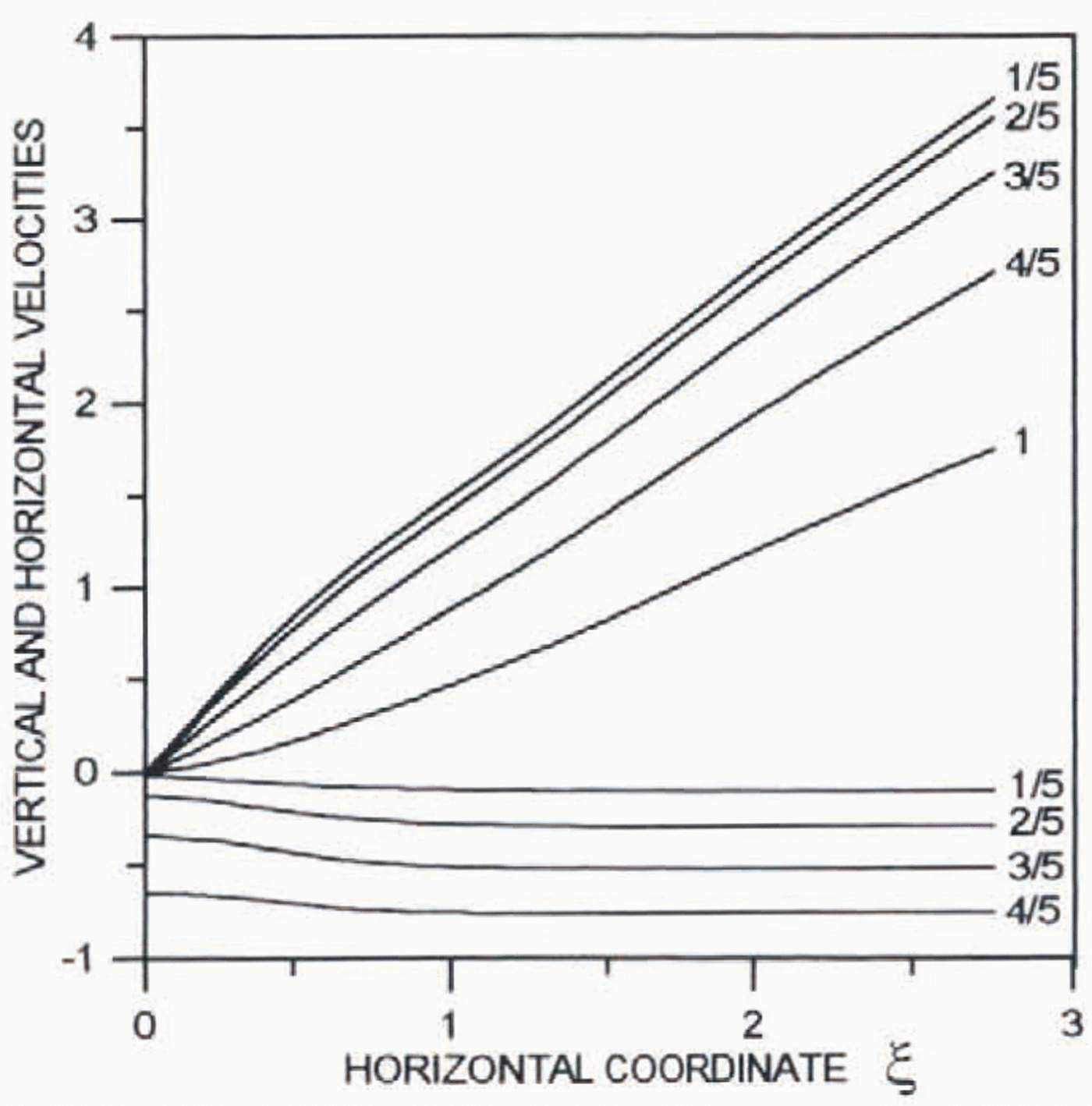
Figures 4–6 present distribution of the horizontal (∂ξ₀/∂y) (positive) and vertical (–∂ξ₀/∂ξ) (negative) velocities as well as the deviatoric shear μ ₀(∂²Ψ₀/∂y ² – ∂²Ψ₀/∂ξ²) and longitudinal 2μ ₀∂²Ψ₀/∂ξ∂y stresses against the horizontal distance ξ . Numbers at the lines show distances from the bed in ice thickness.

Fig. 4. Distribution of the dimensionless horizontal ∂Ψ₀/∂y (positive) and vertical (–∂Ψ₀/∂ξ) (negative) velocities against the horizontal distance from the ice divide. Numbers at the lines show distances from the bed in ice thickness.

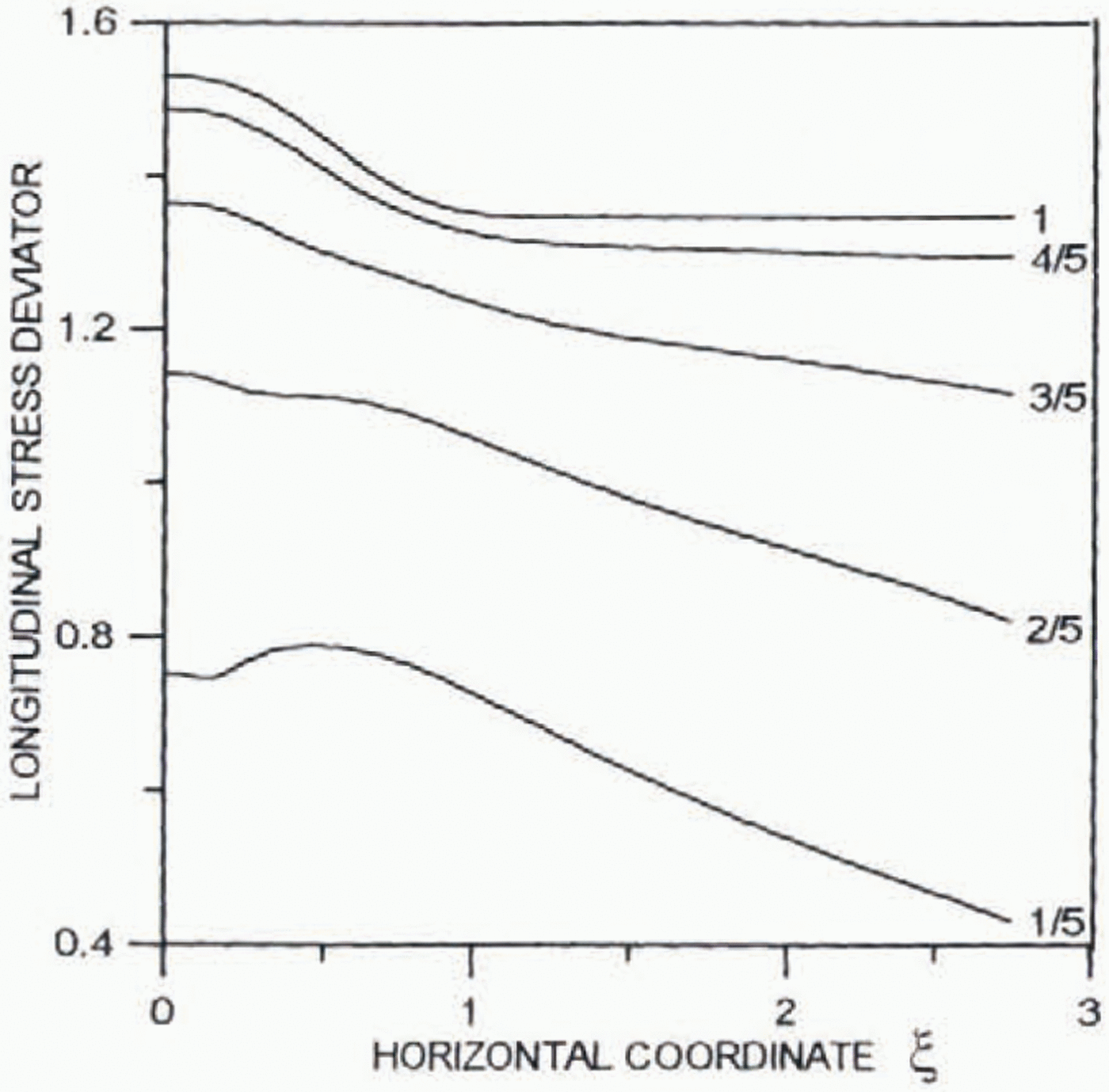
Fig. 5. Distribution of the dimensionless longitudinal deviatoric stress 2μ ₀∂²Ψ₀/∂ξ∂y against the horizontal distance ξ

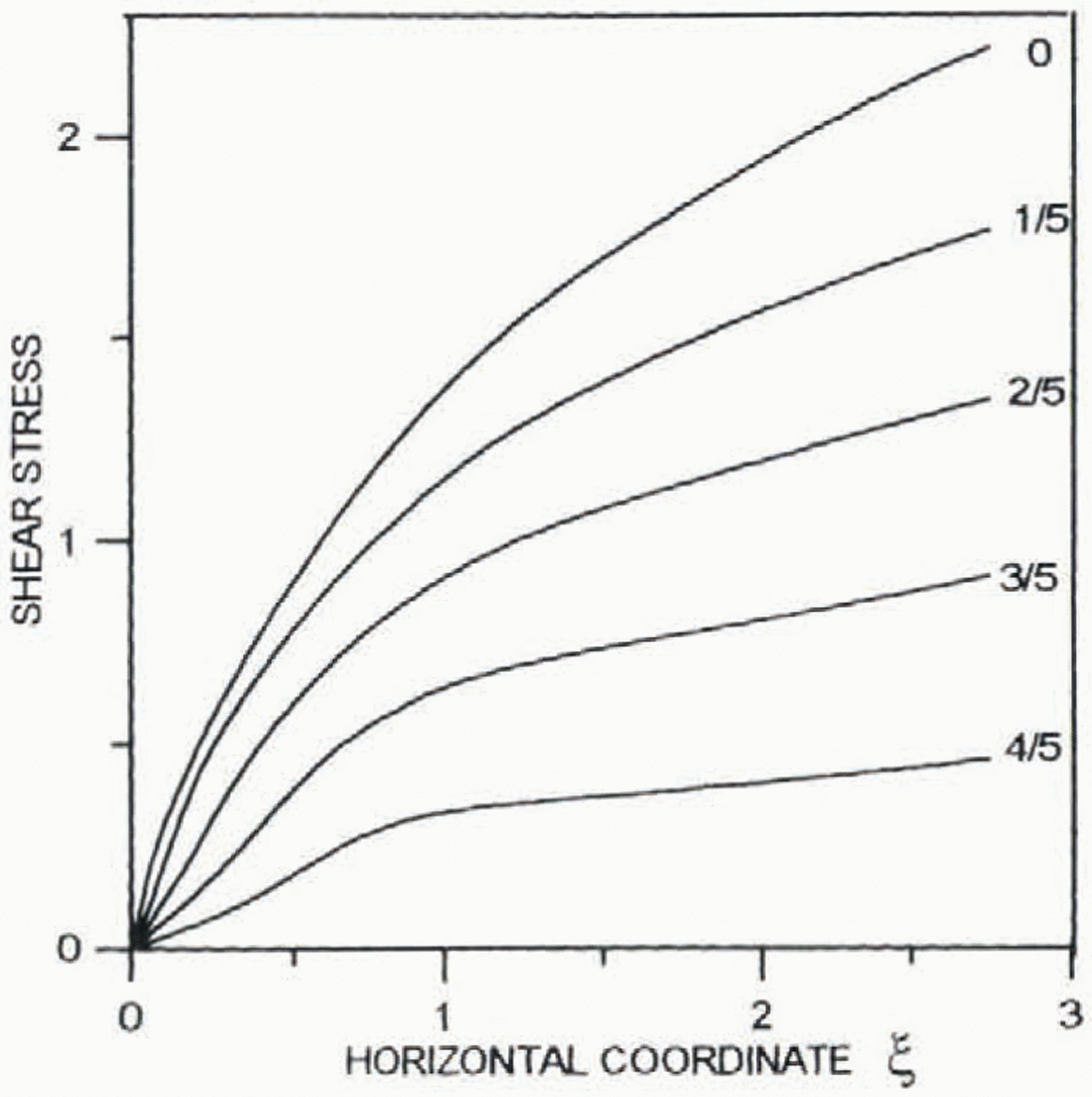
Fig. 6. Distibution of the dimensionless shear stress μ ₀(∂²Ψ₀/∂y ² – ∂²Ψ₀/∂ξ² against the horizontal distance ξ.

5. Conclusions

The study carried out in this paper shows that:

In the vicinity of the ice divide, to order of the glacier-aspect ratio, all unknown characteristics can be searched for in an infinite layer with parallel boundaries, whose thickness coincides with that found by the shallow-ice approximation (far-field solution). Boundary conditions have simplified forms, which are caused by neglecting the bed and ice-surface slopes as well as by independence of the vertical velocity at the glacier surface on the horizontal coordinate.

The problem for the ice divide in the specially scaled variables is stationary; does not depend on the glacier characteristics (glacier length, accumulation rate, flow-law constant, ice thickness) and can be solved separately from the problem for the glacier.

The steady solution found for the ice divide lets us determine non-steady characteristics only by stretching spacial coordinates and the stream function.

The upper-surface curvature is finite at the ice divide.

The shallow-ice approximation is invalid at the ice divide but can be used at a distance from it larger than one ice thickness for determination of the vertical velocity, and at distances larger than six and two ice thicknesses for finding the horizontal velocity and the shear stress, respectively.

Results for the radial case can be derived by the same procedure as for the linear one. In that case, all derived estimates as to the upper-surface slope and the ice thickness at the ice divide do not change.

Perturbation analysis can also apply to the non-isothermal case. The problem for the ice divide will be non-steady due to the temperature distribution. The fact that most glaciers are essentially non-isothermal changes values of all characteristics (Morland and Smith, 1983; Raymond, 1983); however, the kinematic peculiarities of the ice divide seen in the isothermal case will still be present in the non-isothermal case (Dahl-Jensen, 1989).