Modelling the evolution of Vadret da Morteratsch, Switzerland, since the Little Ice Age and into the future

Abstract

We use a 3-D higher-order glacier flow model for Vadret da Morteratsch, Engadin, Switzerland, to simulate its strong retreat since the end of the Little Ice Age (LIA) and to project its future disintegration under a warming climate. The flow model, coupled to a 2-D energy-balance model, is initialized with the known maximum glacier extent during the LIA and subsequently forced with mean monthly precipitation and temperature records. To correctly reproduce the observed retreat of the glacier front for the period 1864–2010, additional mass-balance perturbations are required to account for uncertainties in the initial state, the mass-balance model and climate variations not captured by the ambient meteorological records. Changes in glacier volume and area are in good agreement with additional information from historical topographic maps. Under constant 2001–10 climate conditions, a strong retreat and mass loss continue and Vadret da Morteratsch disconnects from its main tributary, Vadret Pers, before 2020. The future glacier evolution is analysed in detail to understand the timing and rate of retreat, and to assess the role of ice dynamics. Assuming a linearly increasing warming of >3°C by 2100, only isolated and largely stagnant ice patches remain at high elevation.

1. Introduction

In recent decades, mountain glaciers worldwide have lost a significant fraction of their volume in response to the global temperature increase (Lemke and others, 2007). This volume loss is crucial as glaciers are projected to be major contributors to sea-level rise over the next century, with estimated contributions of up to 25 cm (Kaser and others, 2006; Radić and Hock, 2011; Marzeion and others, 2012; Radić and others, 2014). In addition, these ice losses have an important impact on the local water supply and the hydrological cycle (Immerzeel and others, 2010, 2012; Kaser and others, 2010; Farinotti and others, 2012), tourism (Elsasser and Bürki, 2002; Pütz and others, 2011) and risk management (Haeberli and others, 1989; Frey and others, 2010; Werder and others, 2010). The rate of glacier retreat is, however, regionally variable and depends on local factors such as mass balance, glacier geometry, debris cover and orientation (Carrivick and Chase, 2011). The resulting variety in glacier settings strongly complicates general statements about the future evolution of glaciers worldwide. Recent studies based on scaling arguments have attempted to provide a global estimate of the future mass loss of mountain glaciers (Radić and Hock, 2011; Marzeion and others, 2012; Slangen and others, 2012; Radić and others, 2014), but detailed studies of individual glaciers remain essential to assess their reliability. In particular process-based model studies of individual glaciers are needed to improve our understanding of the factors controlling their evolution and to refine global estimates of future sea-level rise from glaciers and ice caps.

Since the end of the Little Ice Age (LIA), alpine glaciers have retreated significantly, a trend that has accelerated over the last few decades and is expected to persist in the coming century (Zemp and others, 2006; Braithwaite and others, 2013). Individual rates of retreat and mean mass balances differ strongly between alpine glaciers and show a non-uniform pattern (Huss and others, 2010a; Lüthi and others, 2010). To properly understand these differences, several modelling studies were conducted focusing on the retreat history. Such studies mainly relied on simple one-dimensional (1-D) flowline models (e.g. Wallinga and Van de Wal (1998) on Rhonegletscher, Switzerland; Zuo and Oerlemans (1997) on Pasterzenkees, Austria) or 2-D models based on the shallow ice approximation (SIA) (e.g. Le Meur and Vincent (2003) on Glacier de Saint-Sorlin, France). Recently, more complex 3-D flow models have successfully been applied to model the past and future evolution of glaciers such as Rhonegletscher (Jouvet and others, 2009) and Grosser Aletschgletscher, Switzerland (Jouvet and others, 2011; Jouvet and Funk, 2014).

Here we present a 3-D higher-order modelling study on the transient behaviour of the Morteratsch glacier complex, Switzerland, from the end of the LIA until 2100. Owing to its relatively long response time, ‘the time a glacier takes to complete most of its adjustment to a change in mass balance’ (Cuffey and Paterson, 2010), the glacier’s past evolution must be modelled before any future projections can be made. Therefore the model is first dynamically calibrated with the observed retreat since the LIA. The Morteratsch glacier complex is well suited for such a study. Indeed, it has been well monitored with a good temporal and spatial data coverage based on topographic maps, direct field evidence and other historical sources. Moreover, both the surface-energy-balance model and the ice-dynamics model have been well validated using data from more than a decade of glaciological observations on surface mass balance, ice thickness and flow velocity (Nemec and others, 2009; Zekollari and others, 2013).

2. Location, Data and Models

2.1. Morteratsch glacier complex

The 16 km² glacier complex is located in southeastern Switzerland (tongue at 46.43°N, 9.93° E in 2012) and consists of two distinct glaciers: the main Vadret da Morteratsch (with a length of 6 km) and its tributary, Vadret Pers (~4.5 km) (Fig. 1). At present, the glacier front is at an elevation of ~2100 m, while the highest parts are ~2000 m higher and correspond to mountain tops such as Piz Bernina (4049 m), Piz Zupo (3996 m) and Piz Palü (3905 m). These peaks prevent direct insolation on the glacier by shadowing for a large part of the year and therefore affect the surface mass balance.

Fig. 1. Annual surface mass balance averaged over the period 2001–10. The map uses the Swiss CH1903 coordinate system. The thick black line delineates the Morteratsch glacier complex; the thin black lines are surface-elevation contours at 200 m intervals (indicated from 2200 to 3800 m). Note that only ice that flows into the glacier complex is considered in the mask, and that isolated small glaciers, such as Vadret da la Fortezza (situated between Vadret Pers (P) and Vadret da Morteratsch (M)), are not taken into account. The highest surrounding peaks are Piz Bernina (PB, 4049 m), Piz Zupo (PZ, 3996 m) and Piz Palü (PP, 3905 m). The inset in the upper right corner shows the location of the glacier in Switzerland.

2.2. Field data

Starting in 2001, we have collected an elaborate dataset on field observations. The ice thickness was measured with different ground-penetrating radar (GPR) systems and subsequently extrapolated over the entire glacier assuming plastic flow along central flowlines. Based on this, we estimate that the glacier volume in 2001 was 1.14 ± 0.28 km³ (Zekollari and others, 2013). Since 2001, we have measured the annual mass balance with ablation stakes, resulting in a dataset of 186 individual measurements so far, which have also been used to deduce the surface velocity of the glacier (error within the order of 1 m a⁻¹). We also performed accumulation measurements with aluminium poles. The absolute movement of all stakes is known from GPS measurements (error within the order of 1 m in the three dimensions). For sites near the ice front where horizontal displacements are virtually nil, this directly provides the thinning rate.

2.3. Ice-dynamic model

A 3-D isothermal ice-dynamic model (Fürst and others, 2011) with Blatter/Pattyn-type equations (Blatter, 1995; Pattyn, 2003) is used, for which the rate factor for temperate ice A ₀ and sliding parameter A _sl were tuned to match observed surface velocities (Zekollari and others, 2013). Nye’s generalization of Glen’s flow law is used to describe the internal deformation (Glen, 1955; Nye, 1957):

(1)

where τ_ij are the deviatoric stresses, n is the power-law exponent (equal to 3 in this study) and is a small offset of 10^–30 to prevent infinite effective viscosity (η) when the strain rate is zero (following Pattyn, 2003). The effective stress is determined by the second invariant of the strain-rate tensor:

(2)

for which the components of the strain rate tensor ε _ij are defined as

(3)

and u_i are the 3-D components of the velocity vector.

Equations (1–3) are simplified to obtain an LMLa (multi-layer longitudinal stresses) higher-order model (Hindmarsh, 2004; Fürst and others, 2011). Assuming local cryostatic equilibrium, bridging effects are neglected in the force balance, and horizontal gradients in the vertical velocity field are assumed to be negligible in comparison with vertical gradients of horizontal velocity. Under these approximations, the horizontal and vertical velocity fields are decoupled, and the latter can be determined via mass conservation. The basal drag τ _b corresponds to the sum of all basal resistive forces and is calculated following the higher-order approximation (Weertman, 1964; Van der Veen and Whillans, 1989):

(4)

(5)

for which b is the bedrock elevation and τ_ij are the components of the stress tensor at the base. The best fit between observed and modelled velocities (root-mean-square error (RMSE) of 15.0 m a⁻¹) was obtained for a rate factor A ₀ of 1.6 × 10⁻¹⁶ Pa⁻³ a⁻¹ and a sliding parameter A _sl of 12 × 10⁻¹⁶ m⁷ N⁻³ a⁻¹ (Zekollari and others, 2013). The highest flow velocities are reached for Vadret da Morteratsch and go up to 125 m a⁻¹ (see Fig. 7 in Zekollari and others, 2013). For Vadret Pers, both the rate factor A ₀ and sliding parameter A _sl were doubled for a better match between observed and modelled velocities and to avoid Vadret Pers becoming too thick in transient simulations. Flow-law parameters are kept constant in time. The model is run on a 25 m horizontal resolution, and in the vertical the grid uses 21 non-equally spaced layers. The flow model is coupled to a surface energy-balance model that determines the spatio-temporal distribution of accumulation and ablation.

The continuity equation is the link between ice dynamics and the surface mass balance:

(6)

where H is the ice thickness, ū is the vertically averaged horizontal velocity vector, ▽ is the 2-D divergence operator and M is the surface mass balance. The higher-order velocity field and changes in ice thickness are calculated with a weekly time step (Δt = 0.02 years), while the mass balance is updated annually. More details on parameter choices, boundary conditions and numerical implementation are provided by Zekollari and others (2013) and Fürst and others (2011).

2.4. Mass-balance model and climatic input

To compute the surface mass balance we use a 2-D energy-balance model (Oerlemans, 2001) that has been calibrated for the Morteratsch glacier complex (Nemec and others, 2009). The model is based on an equation for the cumulative mass balance B (m w.e. a⁻¹) and accounts for the shading effect of the surrounding mountains, the daily temperature cycle, the timing of precipitation events, and seasonal changes in snow thickness and albedo:

(7)

Here L _m is the latent heat of melting (3.34 × 10⁵ J kg⁻¹), ρ _w is the water density (1000 kg m⁻³) and P _solid(t) is the solid precipitation. The time step Δt is 1 hour.

The net energy flux ψ (W m⁻²) at the surface is represented by

(8)

where the first term on the right-hand side is the net shortwave radiation received at the glacier surface, with τ the transmissivity of the atmosphere and α the surface albedo. Q (W m⁻²) is the incoming solar radiation, which consists of a direct and an indirect (diffuse) term and is corrected for the slope and orientation of the glacier surface (Nemec and others, 2009). The term c ₀ + c ₁ . T _air represents the sum of the net longwave radiation and the turbulent heat exchange (Oerlemans, 2001). Here, c ₀ = –45 W m⁻², c ₁ = 12 W m⁻² °C⁻¹, τ = 0.45 (Nemec and others, 2009) and T _air is the air temperature (°C). The parameter values, in particular for τ, were obtained from a best fit of the energy-balance model with our observed mass-balance measurements, and are further informed by detailed observations from an automatic weather station placed in the lower ablation area (personal communication from J. Oerlemans, 2008). The fraction of solid precipitation depends on the local air temperature. Total precipitation is upscaled from nearby weather stations using a fixed altitudinal gradient, and accounts for the timing and intensity of precipitation events informed by a daily precipitation series from a nearby valley station for the period 1981–2006. As discussed in Nemec and others (2009), available data do not allow a further differentiation of snow accumulation with respect to wind exposure, for example, making the precipitation treatment probably the largest source of uncertainty in the calculation of the net mass balance. The cumulative mass balance B after a full balance year (1 October to 30 September) gives the annual specific mass balance, M, needed in Eqn (6).

Meteorological data from surrounding weather stations were used to calibrate the model to ablation and accumulation measurements on both Morteratsch and Pers glaciers for the period 2001–06 (Nemec and others, 2009). Most measurements are available for the ablation zone, while for the accumulation zone we rely on a handful of measurements from aluminium poles, snow pits and a shallow ice core that was drilled by a Swiss group under Piz Zupo (Sodemann and others, 2006). The climatic input to drive the mass-balance model consists of a monthly temperature record from Segl Maria (46.44 ° N, 9.77 ° E, 1798 m a.s.l.) since 1864 and monthly precipitation measurements from Samedan (46.53 ° N, 9.88 ° E, 1705 m a.s.l.) extending back to 1861 (Fig. 2). These data originate from the HISTALP database (Auer and others, 2007) and were homogenized to reduce errors such as the early instrumental warm-bias (Frank and others, 2007; Böhm and others, 2010). The modelled annual mass balance field-averaged over the decade 2001–10, using the topography from a digital elevation model (DEM) of 2001 (DHM25 from SwissTopo; uncertainty 3–6 m), is shown in Figure 1. For this period, the Morteratsch glacier complex has a mean specific mass balance of –0.93 m w.e. a⁻¹ and an accumulation-area ratio (AAR) of 44%, clearly indicative of a glacier out of equilibrium with the imposed climate due to a disproportionally large snout characterized by high ablation. The associated average equilibrium-line altitude (ELA) over this period is ~3020 m for Vadret da Morteratsch, while for Vadret Pers it is ~3080 m. The higher ELA and generally more negative surface mass balance for Vadret Pers are due to glacier orientation. For a large part of the day, most of Vadret Pers is directly exposed to the sun, whereas Vadret da Morteratsch is oriented to the north and receives more shading from the high surrounding peaks (especially from Piz Zupo before noon and from Piz Bernina in the afternoon).

Fig. 2. Annual precipitation measured in Samedan (1861–2010) and average summer temperature (May–September) as recorded in Segl Maria (1864–2010), corrected for early instrumental warm-bias. The homogenized data come from the HISTALP database. The blue lines represent annual values, and the red line represents the 20 year running mean.

2.5. Specific model set-up

Several rock outcrops exist around the ELA and within the accumulation area of the glacier. Most of them are persistent features since the LIA, as identified on topographical maps (1: 50 000) from 1851 (Maisch and others, 1999) and 1935 (DEM provided by F. Paul). These ice-free areas are very steep, and consequently icefall and wind drift prevent permanent snow or ice cover. Our glacier model does not account for the details of this effect, so these parts are kept ice-free in all simulations. However, it is reasonable to assume that snow falling on these ice-free parts will ultimately end up on the glacier and thus contribute to its mass balance. In the model this is achieved by redistributing the positive mass balance of these regions over an elevation band down to 50 m below the specific ice-free part. An additional issue related to keeping these zones ice-free is that mass is lost when ice flows into these regions, which is the case when the downward surface slope is directed towards the outcrops. In reality this process coincides with ice avalanches that fall on lower parts of the glacier. To take this into account, a similar method to that for the snowfall is used and the mass that flows into the ice-free zones is redistributed over the same elevation bands as for the snow. As the glacier geometry hardly changes in the accumulation zone and to avoid ice flowing over ridges away from the glacier (e.g. to the south, towards Italy), the glacier is not allowed to expand laterally above 3000 m of elevation. These modifications ensure that mass is conserved over the glacier complex at all times.

2.6. Past glacier evolution (1850s to 2010)

An array of observational data is available to reconstruct the retreat history of Morteratsch glacier since the LIA. These data are required for the dynamical calibration of the ice-flow model before any future projections.

2.6.1. Record of front position

The front position has been well known since 1878 and serves as a first criterion to reconstruct the past evolution of the glacier complex (Glaciological Reports, 1881–2010). As the snout of Morteratsch glacier has a clear north–south orientation, changes in glacier length follow almost exactly the y –direction of the CH1903 coordinate system (Fig. 1). Therefore the retreat of the front as found in the Glacio-logical Reports (1881–2010) is considered to be in this direction and moreover assumed to refer to the most northerly position of the tongue. Note that for most Swiss glaciers the retreat is not just in one direction, and often corrections are needed as the cumulative length change shows discrepancies with known front positions from different sources (S. Wiesmann and A. Bauder, unpublished information).

2.6.2. LIA extent

The causes and timing of the LIA and the maximum extent of alpine glaciers remain uncertain, as temperature records show no clear cooling followed by a warming for this period (Vincent and others, 2005; Mann and others, 2008; Böhm and others, 2010). In the literature, it has been suggested that an increase in winter accumulation between the 1760s and 1830s may have caused the advance (Vincent and others, 2005). A subsequent decrease in accumulation should then have been responsible for the retreat from this maximum extent (Vincent and others, 2005), perhaps enhanced by a small increase in temperatures associated with a positive phase of the Atlantic Multi-decadal Oscillation (AMO) index between 1850 and 1870 (Huss and others, 2010a). Other recurrent hypotheses link the 19th-century glacier maximum to volcanic eruptions and aerosol forcing (Crowley, 2000); Goosse and others, 2006; Painter and others, 2013; Lüthi, 2014).

For the Morteratsch glacier complex, the maximum LIA extent occurred between 1860 and 1865, somewhat later than many (smaller) Swiss glaciers (Maisch and others, 1999; Oerlemans, 2007). The maximum LIA glacier extent is well known from its end moraine and extends to ~147 200 m (CH1903 y –coordinate), or ~150 m further north than its 1851 extent derived from topographic maps (Maisch and others, 1999). Even for the LIA maximum extent, Vadret da la Fortezza, situated between Vadret Pers and Vadret da Morteratsch, did not coalesce with the main glacier trunk as indicated by morainic and historical evidence. Except for a very narrow lateral connection through which almost no ice flows (as it is not along the steepest gradient), Vadret da la Fortezza has always been an isolated glacier. Therefore it is not considered part of the Morteratsch glacier complex here.

2.6.3. Retreat from the end of the LIA to present day

Up to the beginning of the frontal position record in 1878 (Glaciological Reports, 1881–2010), the glacier retreat from the LIA maximum was only 75–100 m. Since then, the glacier has continuously retreated, with only five exceptional years of standstill or a small advance. Vadret da Morteratsch hardly reacted to the small climatic perturbations that caused other Swiss glaciers to advance in the 1920s and 1980s (Glaciological Reports, 1881–2010), probably because of its longer response time. In general, the retreat history can be divided into four stages:

1. 1. From the beginning of the length record until 1940 the retreat rate is almost constant at 10–15 m a⁻¹. The glacier retreats from its maximum LIA extent, which is too large for the prevailing mass-balance and climatic conditions.

2. 2. Subsequently a period of stronger retreat lasts from 1940 to 1965, during which the frontal retreat rates double to 30 m a⁻¹. This accelerated retreat possibly relates to an increase in solar radiation (Huss and others, 2009) and higher temperatures starting in the 1930s. The latter result from anthropogenic greenhouse gas emissions and a positive phase of the AMO index (Huss and others, 2010a). The faster retreat is verified for other Swiss glaciers (Glaciological Reports, 1881–2010), but for smaller glaciers the period is usually shorter (from 1940 until 1950–55).

3. 3. Between 1965 and 1990, retreat rates decrease to a level similar to that immediately after the LIA. This may relate to an increase in aerosol concentrations (Ramanathan and others, 2001), leading to lower atmospheric transmissivity (Wild and others, 2005) and more cloud formation (Krüger and Grassl, 2002). The resulting reduction in incoming solar radiation had a positive influence on the glacier mass balance (Huss and others, 2009).

4. 4. From the 1990s onwards this effect weakens, and warming due to a further increase in greenhouse gas concentrations dominates. Apart from the anthropogenic effect, the positive phase of the AMO also contributed significantly to the recent warming in the Alps and the associated more negative glacier mass balances (Knight and others, 2005; Huss and others, 2010a). Glacier retreat rates increased again to 30 m a⁻¹ during the last decade.

3. Dynamic Calibration Over the Historical Period

To make realistic projections of the future glacier response, it is important to simulate its flow history as the current glacier is still responding to past changes in climate, geometry and dynamics. To this end, the flow model is first dynamically calibrated to correctly reproduce the observed glacier retreat since the LIA.

3.1. LIA extent of the glacier

The initial condition of the simulation is a glacier in steady state at the LIA extent. Although there is no reason to a priori suspect a steady state around 1864, it is imposed to avoid an unwanted model drift at the start of simulations. Figure 3 shows the corresponding geometry resulting from the flow model. To obtain this glacier extent, the surface mass balance was calculated with average climate conditions for the period 1864–93, which is the first 30 year period for which homogenized HISTALP data from nearby stations are available. However, to obtain the desired glacier length it was necessary to apply an additional mass-balance forcing of +0.5 m w.e. a⁻¹, corresponding to an ELA lowering of ~60 m. This seems reasonable, as the mass balance over the glacier was very likely more positive at the end of the LIA.

Fig. 3. Modelled steady-state thickness field for a glacier with the same length as indicated by the LIA moraine. The contours are spaced 50 m apart. The thick black line indicates the ELA. White areas are either ice-free or contain ice that does not contribute to the flow of the glacier complex.

For the modelled LIA geometry the glacier volume is 2.25 km³ and the thickest ice for central Morteratsch glacier is found at 410 m. The ELA is ~200 m lower than the 2001– 10 average at ~2820 m for Vadret da Morteratsch and 2880 m for Vadret Pers. As a result of the steady-state configuration the mean specific mass balance of the glacier complex, which is the annual surface mass balance averaged over the whole glacier, is equal to zero.

3.2. Evolution of the glacier from 1864 to 2010

From the balance year 1864/65 onwards, the surface mass balance B is calculated from the 2-D energy-balance model driven by the Segl-Maria and Samedan temperature and precipitation records. In the dynamic calibration process, a mass-balance correction δB is iteratively applied to best match the observed evolution of the frontal position as follows:

(9)

Here B is a function of location (x, y) and time t, B _SMB is calculated from the energy-balance model and δB (t) is considered uniform over the glacier. The mass-balance correction implicitly accounts for deviations from the initial steady-state assumption, uncertainties in the mass-balance model and errors in the climatic-forcing records. This correction varies in time and is necessary to reproduce the observed retreat. This approach to generate the current glacier imbalance is similar to Oerlemans (1997) in a study on Nigardsbreen. Norway, and is applicable when the glacier-length record exceeds the characteristic response time (Zuo and Oerlemans, 1997; De Smedt and Pattyn, 2003).

Figure 4 shows the required mass-balance correction δB (t), which was determined manually in order to reproduce the main frontal retreat trends. It can conveniently be expressed as four piecewise linear sections representing different periods between 1864 and 1960. The initial δB is kept constant at +0.5 m w.e. a⁻¹ until 1905. Without keeping this positive mass-balance correction, the modelled retreat would have been too strong. After 1905, δ B had to decrease to 0.1 m w.e. a⁻¹ by 1930 to capture the accelerated retreat starting in the 1930s. A further positive mass-balance correction of maximally +0.5 m w.e. a⁻¹ centred around 1945 was required to correctly simulate the smaller glacier retreat rates during the 1970s and 1980s. In this paper we can only speculate about the reasons why a surface-mass-balance model driven by HISTALP data alone is not able to produce a correct glacier retreat. Apparently, the glacier’s mass balance is affected by additional features not captured well in the ambient climate records, as noted earlier, for example in a study on Glacier d’Argentière, France (Huybrechts and others, 1989), and a recent study by Lüthi (2014). Possibly this is related to variations in aerosol content (Huss and others, 2009; Painter and others, 2013). The absence of a mass-balance correction after 1960 to correctly simulate the glacier retreat of the last 50 years does, however, lend credibility to the dynamic calibration as performed here. It clearly suggests that the effect of the initial steady-state assumption has faded by 2010 and that the surface-mass-balance model driven by unbiased HISTALP data over recent decades produces a basically correct forcing for the glacier flow model.

Fig. 4. Modelled and observed glacier length evolution of Vadret da Morteratsch between 1878 and 2010. An additional mass-balance correction (shown in blue) is required for a better match of the modelled frontal retreat with the observations and is set to zero after 1960.

Other sources of information have been used to validate the glacier model. Huss and others (2010b) reconstructed the evolution of the Morteratsch glacier volume between 1900 and 2008 based on mass-balance modelling and absolute volume differences derived from four DEMs for 1935, 1955, 1985 and 2008. Overall, there is a good agreement between the results of Huss and others (2010b) and our volume change reconstructions (Fig. 5), especially after 1960 when the mass-balance correction is no longer applied. In both cases, the same general trends are captured, including two phases of higher volume-loss rates. Interestingly, these two phases (1925–1960 and from 1980 onwards) precede the associated periods of accelerated frontal retreat by ~5–10 years. This is because glacier volume is known to adapt faster to climatic changes than glacier length (e.g. Oerlemans, 2001; Adhikari and others, 2011). This can also be inferred from the evolution of glacier area shown in Figure 5, which mainly reflects length changes at the snout. Huss and others (2010b) derived a volume loss of 0.61 km³ between 1935 and 2008, compared with 0.58 km³ from our ice-dynamic model. For the more recent period between 1985 and 2008, the volume losses are respectively 0.305 km³ and 0.316 km³. Fischer and others (2014), also based on DEM differencing, obtain a volume loss of 0.30 km³ between 1991/92 and 2008/09, while we obtain 0.27 km³ for this period.

Fig. 5. Reconstructed cumulative volume change (relative to 2008) and area change (2 year running mean) for the Morteratsch glacier complex between 1864 and 2010. The reconstruction by Huss and others (2010b) is based on mass-balance modelling, constrained by four fixed points derived from DEM differencing.

The recent increase in mass loss and the subsequent accelerated frontal retreat has its counterpart in the long-term mean specific mass balance of the Morteratsch glacier complex. Centred around 1980, the 20 year average annual surface mass balance of the glacier is around –0.21 m w.e. a⁻¹, while only 20 years later, in 2000, this value lowers to –0.82 m w.e. a⁻¹. From the meteorological records shown in Figure 2, it is clear that the recent glacier retreat is primarily driven by higher summer temperatures.

Additionally, the modelled 2001 glacier state is compared with the observed glacier geometry (Zekollari and others, 2013). As shown in Figure 6, there is overall quite good agreement between the modelled surface topography and that from the DEM. As the bedrock is kept constant in the modelling, good agreement also applies to the ice thickness. The highest ice thickness of ~350 m is found for central Vadret da Morteratsch in both fields. The maximal ice thickness for Vadret Pers is equally 250 m in both cases. The total ice volume obtained from the transient model run in 2001 (1.41 km²) is, however, situated at the high end of the range inferred from available radar observations (1.14 ± 0.28 km³) (Zekollari and others, 2013). This may reflect shortcomings in the assumptions made to generalize the radio-echo sounding lines over the whole glacier to reconstruct ice thickness, as well as in the flow parameters used in the ice-dynamic model. The largest discrepancies between observed and modelled ice thickness occur for the tongue, the confluence area and the accumulation area of Morteratsch glacier. However, the last zone lacks meaningful ice thickness and velocity measurements. One explanation is that the flow model assumption for the ice in the accumulation area is too stiff, because flow parameters were derived from a calibration between glacier geometry and measured surface velocities in the ablation zone. Alternatively, the reconstructed ice thickness in the accumulation zone, inferred from the concept of plastic flow with a constant yield stress, may be an underestimate. Quite possibly the real ice thickness in the accumulation zone and the real ice volume in 2001 are much closer to the modelled estimate of 1.41 km³.

Fig. 6. Ice thickness distribution in 2001, derived from field measurements (Zekollari and others, 2013) (a) and from the transient model run (b). The contours represent the difference in ice thickness (m) between the two methods.

A final comparison can be made between the surface mass balance predicted by the energy-balance model and the actual stake readings from our observations. RMSEs for individual balance years vary between 0.5 and 1.0 m w.e. a⁻¹ and are similar to those obtained during the model calibration by construction (Nemec and others, 2009). The largest discrepancies are found in the lower part of the glacier for the warmest years. However, the deviations have a stochastic component and did not prevent the model from correctly reproducing the recent glacier evolution as discussed above.

4. Future Glacier Evolution to 2100

4.1. Climatic-forcing scenarios

With the past evolution of the glacier well constrained, the simulations can be extended into the future. To force the future mass balance we use climatic scenarios inspired by the CH2011 (2011) projections for the 21st century over Switzerland. These are based on output from global climate models (GCMs) that are coupled to European-scale regional climate models (RCMs). CH2011 considers three Inter-governmental Panel on Climate Change (IPCC) scenarios, of which two are non-intervention scenarios (A2 and A1B) and a third is a climate-stabilization scenario (RCP3D, emissions cut by 50% in 2050 compared with 1990). With respect to 1980–2009, the different GCM/RCM combinations and scenarios result in a mean temperature increase in 2070–99 in the range of +0.8 to +2°C (RCP3PD scenario) and 2.7°C to +5.0°C (A2 scenario). For the Alpine region, the warming in all RCMs is most pronounced in the summer months. Also the change in precipitation shows a seasonal character, with wetter winters (between +0% and +30% precipitation) and drier summers (–30% to 0%). This is in line with the results of the PRUDENCE project (Prediction of Regional scenarios and Uncertainties for Defining European Climate change risks and Effects; Christensen and Christensen, 2007). Based on these climate projections, we construct nine schematic warming scenarios that broadly cover the range of CH2011 scenarios. We opted for schematic scenarios as the interest is in the main future climatic trends and not in a specific scenario-model set-up. As a control we also consider three scenarios with no temperature increase. The nine warming scenarios consist of a combination of three linear warming trends (+1.0°C, +2.5°C and +4.0°C of mean annual warming between 2010 and 2100) and three precipitation trends (neutral, wet and dry). The changes are applied with respect to the 2001–10 averages of the monthly mean temperature and precipitation data. For all scenarios, the summer (June–July–August) warming lies 25% of the annually averaged warming above the warming of the other seasons: for example, the +4.0°C scenario corresponds to a temperature increase of +4.75°C for the summer and +3.75°C for the other seasons. The wet scenario accounts for a linear 30% increase of winter precipitation by 2100, an increase of 15% for spring and autumn and no change in summer precipitation. In the dry scenario the summer precipitation linearly decreases by 30%, the spring and autumn by 15% and the winter precipitation remains unchanged. For the neutral precipitation scenario, future precipitation rates are kept constant at their 2001–10 level.

4.2. Projections of ice volume and ice extent

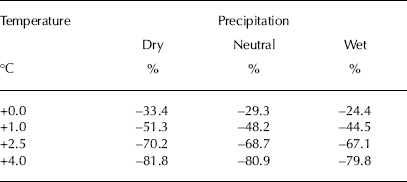
Figure 7 and Table 1 summarize the projected evolution of glacier volume. Under all scenarios a strong mass loss is expected. This includes the no-warming scenario, in which the glacier still loses between 24.4% and 33.4% of its volume by 2100 depending on whether precipitation rates increase, decrease or remain stable. This provides a clear manifestation of the current imbalance of Morteratsch glacier and of the time needed to equilibrate towards 2001– 10 mass-balance conditions. For the highest warming scenario considered here (+4.0°C), ice volume by 2100 is reduced by 80% relative to 2010. For all warming scenarios, ice loss continues beyond the 21st century. On the other hand, up to 2020 the glacier evolution does not depend on any particular scenario and is almost entirely conditioned by past climatic changes, in particular the post-1970 warming. Strikingly the effect of precipitation changes is small compared with the effect of temperature changes. Even the adopted increase in precipitation of the wet scenario is not sufficient to counterbalance further glacier retreat for the no-warming case. This relates to the fact that the annual mass balance of Alpine glaciers is mainly driven by their summer balance (Vincent and others, 2004; Zekollari and Huybrechts, 2014).

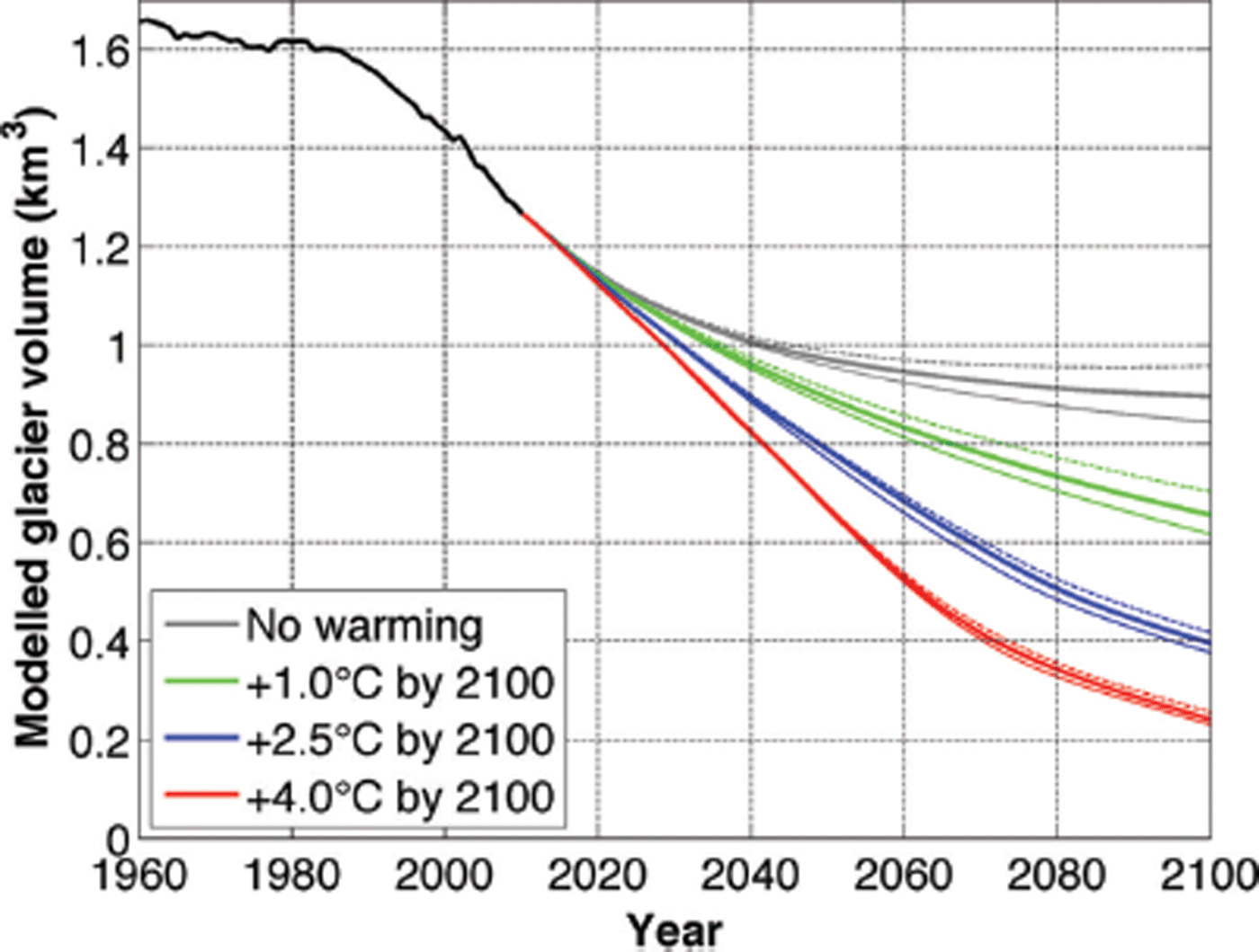
Fig. 7. Future evolution of ice volume under different climate scenarios. The black line represents the reconstructed evolution over the past 50 years. The line colour denotes the temperature scenario, while the line style indicates the precipitation scenario. For a particular colour, the thick solid line represents the ‘neutral’ precipitation scenario, the thin dashed line represents the ‘wet’ scenario and the thin solid line the ‘dry’ scenario.

Table 1. Relative ice volume loss in 2100 compared to 2010 for the different climatic scenarios

The corresponding glacier geometries are shown in Figure 8. By 2030 the glacier has retreated by ~1 km compared with 2010, and Vadret Pers is no longer a tributary of Vadret da Morteratsch. The separation of the two glaciers occurs in the model before 2020. The imminent disconnection of the two glaciers is clearly supported by field observations since 2000 and may perhaps take place as early as 2015 if a remaining frontal ice patch of unknown thickness connecting both glaciers melts completely. For both glacier tongues, the frontal thinning and retreat is almost entirely driven by the local surface mass balance as there is virtually no mass supply from upstream as flow velocities in the tongue area approach zero (Zekollari and others, 2013). Typical ablation rates at the tongue of Morteratsch glacier are 7–8 m w.e. a⁻¹ for the period 2001– 10, and so are observed ice-thinning rates. For the highest-warming scenario (+4.0°C by 2100), the mean ELA has risen by 40–80 m by 2030 to ~3100 m for Vadret da Morteratsch and 3120 m for Vadret Pers.

Fig. 8. Simulated glacier extent and ice thickness for different temperature scenarios (vs 2010) and time periods, assuming neutral precipitation. The ice-thickness scale is the same as that used in Figure 6. The thick black line delineates the DEM glacier outline in 2001, while the thin lines delineate 50 m ice-thickness intervals.

After 2050, the effect from considering different scenarios becomes evident. By 2065, the retreat is stronger for Vadret Pers than for Vadret da Morteratsch, mostly due to thinner ice, a higher ELA and a more negative mass balance in the frontal area. In the +4.0°C warming scenario, the ELA for Vadret Pers rises to 3330 m by 2065, while for Vadret da Morteratsch it rises to ~3315 m. Towards the end of the century the ELA rises to 3520 m for Vadret da Morteratsch and 3500 m for Vadret Pers. This reflects a similar exposure and orientation of the respective glacier sections in this elevation band. Glacier retreat continues up to the end of the 21st century. By 2100, there is a clear distinction between the different scenarios considered. For the two highest-warming scenarios, only ice at high elevations remains and the glacier complex starts to disintegrate into disconnected ice patches. Despite its slightly more negative mass balance, the tongue of Vadret da Morteratsch extends further north than that of Vadret Pers because of its higher ice thickness which takes longer to completely waste away.

Three-dimensional views of the various model simulations discussed above are displayed in Figure 9. In the scenarios with the strongest retreat, it is likely that proglacial lakes will form in bedrock depressions (Zekollari and others, 2013). Their effect is not taken into account here, but can potentially accelerate the glacier retreat by hydrostatic lifting of the glacier front. The formation of future proglacial lakes is also important from a natural-hazards perspective, as some of them form behind natural moraine dams that can easily break, potentially causing serious damage from flash flooding downstream (Haeberli and others, 1989; Frey and others, 2010). Judging from the glacier bed exposed so far, the lake that may form in the central Morteratsch area is, however, probably dammed by hard rock rather than by soft sediment, and so may not be subject to potential failure.

Fig. 9. 3-D view of the glacier from the north-northwest for different settings, scenarios and times. The domain ranges from 789 500 m to 796 000 m in the x –direction and from 137 500 m to 148 000 m in the y –direction following the CH1903 coordinate system. Blue areas denote local bedrock depressions that may hold proglacial lakes after the glacier has retreated.

4.3. Climate–geometry imbalance

Further insight into the future time-dependent response and glacier imbalance is provided by the time evolution of the mean specific mass balance. Figure 10 displays the spatially averaged annual surface mass balance for all future warming experiments with constant (2001–10 average) precipitation. The mean specific mass balance is a measure for the annual rate of mass loss and is a complex function of both the climate state and the actual glacier hypsometry (area– elevation distribution). For constant 2001–10 climate forcing (no-warming scenario), the expected quasi-exponential decay of the glacier imbalance is confirmed. It is caused by geometric adjustment that mainly entails loss of an excess glacier tongue that can no longer be supplied with sufficient ice mass from a reduced accumulation area.

Fig. 10. Future evolution of mean specific mass balance for the different climate scenarios, assuming average 2001–10 precipitation.

By the end of the 21st century, the glacier is still out of equilibrium with the 2001–10 climate, although an asymptotic evolution towards a zero mean specific mass balance is evident. The eventual steady state corresponds to a volume loss with respect to 2010 of between 25% and 35%, depending on the precipitation scenario, and a frontal retreat of almost 2 km for Vadret da Morteratsch and 1.5 km for Vadret Pers (see also Figs 7–9). In this experiment, the associated AAR steadily increases from 44% for the period 2001–10 to 57% in 2065 and 58% in 2100.

From the no-warming case, one can also derive a first estimate of the volume response time of Morteratsch glacier, as the time period during which a fraction of (1 – e⁻¹) or 63% of the imbalance in 2010 of –0.82 m w.e. a⁻¹, derived from the 2001–10 mean climatology, has been overcome. This timescale corresponds to 32 years but is not considered a clean measure of the response time of the current glacier as it also contains a contribution from the cumulated imbalance prior to the 2001–10 period.

For the other warming scenarios, the evolution of the mean specific mass balance results from an interplay between geometric adjustment and a continuously decreasing surface mass balance. In the +4°C scenario the effect of further warming initially dominates and the imbalance increases until 2052. After that period, the loss of surface area is more pronounced and this increases the mean specific mass balance faster than the warming decreases it. The complex evolution of the imbalance in a changing climate illustrates the difficulty of deducing a climatic signal from changes in glacier geometry. For this purpose the reference surface mass balance, the mass balance on a fixed surface at a certain reference date (Elsberg and others, 2001; Huss and others, 2012), should be used. Over the 21st century, the glacier’s reference surface mass in our experiments is found to increase continuously for all warming scenarios (i.e. it becomes less negative).

5. Discussion

5.1. Comparison with other studies

Comparable studies simulating the future 3-D geometry of a mountain glacier have been performed by other researchers. Using a distributed accumulation and temperature-index melt model driven by RCMs to estimate ice-thickness changes, Huss and others (2010b) attempted to project the future evolution of the Morteratsch glacier complex. In their modelling, similar climate scenarios were used but ice dynamics was not considered. Instead, they imposed a distributed ice-thickness change based on the observation that elevation changes of retreating glaciers are normally largest near the glacier terminus. Since Huss and others (2010b) also carried out a model calibration over the 20th century, there is reasonable agreement between their projections and ours concerning the evolution of glacier length, area and volume until 2030. Beyond 2030, however, Huss and others (2010b) produce a more fragmented glacier retreat with more isolated patches of ice in the deeper bedrock depressions, which are largely absent from our work as analysed further below.

The relative volume loss of the Morteratsch glacier complex over the 21st century is generally smaller than that of other large Swiss glaciers (Huss and others, 2010b; Farinotti and others, 2012; Salzmann and others, 2012). This difference depends on several factors, such as the sensitivity of the mass balance and differences in climatic scenarios, but is mainly dictated by the specific hypsometry of the glacier in question. Morteratsch glacier stands out in having a comparably large areal fraction in the elevation band between 3500 and 4000 m, which will remain in the accumulation zone even for a warming of +4°C. In another 3-D ice-dynamic simulation, Jouvet and others (2009) find that Rhonegletscher almost entirely disappears by 2100 in their ‘median’ scenario (in between our +2.5°C and +4.0°C scenarios), but that is mainly because Rhonegletscher has its highest point at ~3600 m, eliminating an accumulation area of sufficient size. In another study with the same ice-dynamic model, Jouvet and others (2011) reported dramatic ice losses for Grosser Aletschgletscher by 2100. In their ‘ENSmed’ scenario, close to our +4.0°C scenario, <10% of the 1999 ice volume remains by 2100, less than the ~15% remaining for Morteratsch glacier. For Glacier de Saint-Sorlin (2700–3400 m) Le Meur and others (2007) modelled a total disappearance of the glacier by the end of the 21st century under the IPCC’s SRESB1 scenario. Again, these differences reflect different area–elevation distributions. A common feature of all these studies, however, is the near disappearance of even the largest Alpine glaciers by the end of the 21st century, albeit for a higher-than-average warming scenario.

5.2. The role of ice dynamics

To further investigate the role of ice dynamics in our projections, we considered two additional experiments. These test the role of ice dynamics in different set-ups following the work of Huybrechts and De Wolde (1999). The dynamic response is the one discussed so far in which there is a full coupling between the mass balance and the ice flow. In the static response, the ice flow is kept constant at the year 2010 state (constant flux divergence in Eqn (6)) but changes in ice thickness can still feed back on the mass balance through the mass-balance elevation gradient. For the fixed-geometry response, the ice flow is also kept constant, and additionally changes in glacier geometry cannot feed back on the mass balance (through the mass-balance elevation gradient). Here only perturbations with respect to the 2001–10 mass balance, which are solely climate-driven, are integrated forward in time. This set-up enables us to distinguish between the role of ice dynamics on the one hand and the effect of the height–mass-balance feedback on the other hand.

Figure 11 shows the results. For both the no-warming and the +4°C scenarios the differences in total volume loss by 2100 are within 10% of each other for all three cases. This clearly shows that the dominant response is from changes in the surface mass balance, not from ice dynamics. The static and fixed-geometry cases are most closely aligned, indicating that due to the limited ice thicknesses the height–mass-balance feedback does not play an important role in the future response of an alpine mountain glacier. This is different from the response of ice sheets (Huybrechts and De Wolde, 1999), which have a much larger ice thickness.

Fig. 11. Future evolution of glacier volume under different model set-ups addressing the role of ice dynamics. The upper curves are for the no-warming scenario and the lower curves for the +4.0°C warming scenario.

As time evolves, the inclusion of ice dynamics is found to speed up the total volume loss, and this effect is much more pronounced in the +4°C scenario than in the no-warming scenario. Moreover, keeping the flux-divergence term constant in the static response has an opposite effect on the accumulation and ablation zones. This is demonstrated in Figure 12. Including ice dynamics increases the mass loss in the ablation zone and enhances the retreat of the glacier tongue. This is because the flux-divergence term can adjust to the thinning margin (it becomes less positive) so that less mass is transported to the same position in the tongue area. This is not the case for the static experiment in which the ice-transport term is fixed. In the accumulation zone, on the other hand, excluding ice-dynamic adjustment (static response) increases mass loss and enhances local thinning, so that the glacier disintegrates more easily into separate ice patches than in the dynamic response.

Fig. 12. Glacier geometry in 2100 in the +4.0°C scenario in an experiment including ice-dynamic adjustment (dynamic response, left panel) and excluding ice-dynamic adjustment (static response, right panel). The view is from the north-northwest and coordinates are given in the CH1903 system.

6. Conclusion

Since the end of the LIA, Morteratsch glacier has almost continuously retreated, a trend which recently intensified due to anthropogenic warming and will persist in the future under all scenarios considered here. We were able to reconstruct the past evolution of the glacier in good agreement with field data. However, this required imposing an additional mass-balance bias on top of the surface mass balance calculated with an energy-balance model forced by climatic data from nearby meteorological stations. Apparently, past mass-balance changes were influenced by other processes not well captured in the ambient climate records. The absence of any artificial mass-balance correction after 1960, together with a correctly simulated glacier retreat, lends credibility to the dynamic calibration as performed here. It also indicates that the initial steady-state assumption made for the start of the simulation in 1864 has basically been forgotten by today.

The decadal mean specific mass balance between 2001 and 2010 is found to be –0.93 m w.e. a⁻¹, indicative of the strong disequilibrium between the current glacier geometry and today’s climate conditions. The e-folding volume-response time scale could be estimated at ~30 years. Consequently, the evolution of the glacier in the coming decades is already defined by its past evolution. Irrespective of any scenario considered here, the glacier is found to retreat further by almost 1 km by 2030, and Vadret da Morteratsch disconnects from its main tributary, Vadret Pers, before 2020. Even if the present-day climate were to be maintained, Morteratsch glacier is committed to retreat until at least the end of the 21st century, when it comes near to a new steady state with a volume loss of 25–35% and a frontal retreat of ~2 km compared with the present day. A realistic increase in precipitation can attenuate the future retreat, but cannot stop it. For the two highest warming scenarios (+2.5°C and +4.0°C), in 2100 only ice at high elevations remains and the glacier starts to disintegrate into disconnected ice patches. Glacier retreat is almost entirely mass-balance driven; however, ice-dynamic adjustment is found to accelerate the volume loss by ~10%, producing a less-fragmented ice distribution. If Vadret Pers and Vadret da Morteratsch retreat by >3 km, proglacial lakes are likely to form in bedrock depressions, and this may speed up the retreat under certain circumstances.

Compared with other well-studied Swiss glaciers that have been subjected to similar modelling studies, the 21st-century relative length changes and mass loss of the Morteratsch glacier complex seem to be less dramatic. This can be attributed to its relatively large size and high elevation, especially the large fraction of its area above 3500 m that will probably remain above the ELA, even for a warming of +4°C. Nevertheless, it is clear that the climatic warming realized so far already has a profound effect on Alpine glacierized environments and will commit us to a substantial further ice loss for the next century, even when future warming could be stabilized at relatively low levels.