1. INTRODUCTION
In the past, the Northern Hemisphere has been periodically affected by glaciations. While numerous reconstructions of the last glacial cycle global ice-sheet topography exist, only limited geological evidence of the penultimate glacial cycle or older ice topography is available. Here we focus on the reconstruction of the Northern Hemisphere ice sheets during the Marine Isotope Stage 6 (MIS 6) glacial maximum (~140 ka BP), denoted as the penultimate glacial maximum (PGM).
For the PGM Eurasian ice sheet, an extent considerably larger than its Last Glacial Maximum (LGM; ~21 ka BP) counterpart was provided by the QUEEN project (Svendsen and others, Reference Svendsen2004). In particular, the reconstruction extends further eastwards and southwards over Siberia than during the LGM. However, the advance of the eastern part of the Eurasian ice sheet could have occurred before the PGM, as two other advances during the MIS 6 glacial cycle, at ~160 ka BP and ~180 ka BP, have been identified (Astakhov, Reference Astakhov2004; Svendsen and others, Reference Svendsen2004). While geological evidence of the extent have been retrieved, there are only a few reconstructions of the PGM Eurasian ice-sheet volume. Lambeck and others (Reference Lambeck2006) inverted observations of shoreline elevations change resulting from post-glacial isostatic rebound and obtained a PGM Eurasian ice volume of ~60 m SLE (meters sea level equivalent). Based on the extent of the PGM Eurasian ice sheet from Svendsen and others (Reference Svendsen2004), Peyaud (Reference Peyaud2006) simulated an Eurasian ice volume of ~70 m SLE. The ICE-5G reconstruction by Peltier (Reference Peltier2004) suggested an LGM Eurasian ice-sheet volume of ~22 m SLE. Recently, Kleman and others (Reference Kleman, Fastook, Ebert, Nilsson and Caballero2013) analysed new evidence and simulated a value of ~20 m SLE. In terms of global ice volume, Masson-Delmotte and others (Reference Masson-Delmotte2010) estimated that over the past million years the PGM Eurasian ice sheet only had the sixth largest global ice volume (LGM was seventh), implying that potential past glaciations, larger than the PGM glaciation, could have occurred.
In contrast to the Eurasian ice sheet, there is no geological evidence of the extent and volume of the Laurentide ice sheet older than the LGM. Moraine dating indicates that the LGM extent was the largest glaciation that occurred in North America over the past 400 ka, which suggests that traces of previous glaciations were destroyed during the LGM (Dyke and others, Reference Dyke2002). Naafs and others (Reference Naafs, Hefter and Stein2013) found that ice rafting episodes, produced by surges mostly through the Hudson Strait, were less pronounced during MIS 6 than during the last glaciation. Similarly, the decreased amount of ice rafted debris found north of Grand Banks and off the western Iberian margin suggest a smaller Laurentide ice sheet during the PGM than during the LGM (Hiscott and others, Reference Hiscott, Aksu, Mudie and Parsons2001; Abreu and others, Reference Abreu, Shackleton, Schonfeld, Hall and Chapman2003). On the contrary, ice rafted debris accumulation in the North Pacific indicates that the glaciation over Kamchatka, coastal Alaska and Siberia might have been more extensive during the PGM than during the LGM (St John and Krissek, Reference St John and Krissek1999; Nürnberg and others, Reference Nürnberg, Dethleff, Tiedemann, Kaiser and Gorbarenko2011; Barr and Solomina, Reference Barr and Solomina2014).
As a matter of fact, the lack of evidence about the Laurentide ice-sheet extent at the PGM limits an accurate climate modeling for this time period. For example, Ullman and others (Reference Ullman, LeGrande, Carlson, Anslow and Licciardi2014) and Beghin and others (Reference Beghin, Charbit, Dumas, Kageyama and Ritz2015) demonstrated with idealized experiments that changing the size of the North American ice sheet induces a shift in the planetary waves, thus influencing the climate over Eurasia. In a recent study, Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) tested the impact of ice elevation over North America on the climate of the PGM. They showed that, in agreement with previous studies (e.g. Pausata and others, Reference Pausata, Li, Wettstein, Kageyama and Nisancioglu2011; Ullman and others, Reference Ullman, LeGrande, Carlson, Anslow and Licciardi2014), prescribing a smaller Laurentide ice sheet yields higher temperatures and precipitation rates over the North Atlantic and northern Eurasia, and lower temperatures over East Siberia compared with setting the Laurentide ice sheet as large as during the LGM.
The large uncertainty in the volume of the PGM Eurasian and Laurentide ice sheets and the extent of the latter calls for dedicated ice-sheet modeling studies. To give a reliable estimate of the Northern Hemisphere ice-sheet geometry, we need to explore the parameter space of ice-sheet model uncertainties. This approach was followed by Marshall and others (Reference Marshall, James and Clarke2002) to study the dynamics of the North American ice sheet at the LGM.
The objective of the present paper is to obtain a range of reliable estimates of the PGM Northern Hemisphere ice volume by means of a 3-D thermo-mechanical ice-sheet model. To this end, the ice-sheet model is forced with the two PGM glacial-maximum climates simulated by Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) prescribing different ice elevations over North America. Those two topographies are highly idealized, but using them in the present study allows us to investigate the sensitivity of those two PGM ice sheet reconstructions, which also bear large uncertainties in the Eurasian ice-sheet dimensions, to changes in model parameters. We conduct a large number of univariate steady-state sensitivity experiments, in which parameters related to surface mass balance, thermodynamics, ice-sheet geometry and solid Earth are varied. We perform steady-state simulations, since necessary boundary and forcing conditions for transient simulations are not available. In addition, we use global sea-level reconstructions to put some constraint on the simulated PGM Northern Hemisphere ice volumes. In the following sections, we first describe the ice-sheet model used in the present study as well as the design of the ice-sheet experiments. Then we analyze the ensemble of simulated Northern Hemisphere ice-sheet topographies. Finally, we discuss the various assumptions on which this study relies and draw our conclusions.
2. METHODS
2.1 GRenoble Ice Shelf and Land Ice Model (GRISLI)
To simulate the PGM Northern hemisphere ice sheets, we use the 3-D thermo-mechanical ice-sheet-ice-shelves and ice-stream model GRISLI (Ritz and others, Reference Ritz, Rommelaere and Dumas2001). GRISLI is able to simulate both inland ice using the Shallow Ice Approximation (SIA; Hutter, Reference Hutter1983), as well as ice shelves and ice streams using the Shallow Shelf Approximation (SSA; MacAyeal, Reference MacAyeal1989). GRISLI has been validated over Antarctica (Ritz and others, Reference Ritz, Rommelaere and Dumas2001) and applied to study the inception of the Eurasian ice-sheet growth during the Early Weichselian period (Peyaud, Reference Peyaud2006; Alvarez-Solas and others, Reference Alvarez-Solas2011).
In GRISLI, potential ice stream areas are determined from bedrock topography, assuming that ice streams are located in narrow bedrock valleys. In addition, ice streams are also allowed in areas where a sufficiently thick sediment layer, determined from a map of present-day sediment thickness by Laske and Masters (Reference Laske and Masters1997), is present, which has to be saturated by meltwater, and where the effective pressure N (balance between ice pressure and subglacial water pressure) is low. The SSA is then triggered when those criteria are fulfilled. Ice shelves are treated in GRISLI by means of the SSA. In every time step, the position of the grounding line, and therefore of ice shelves is determined with a flotation criterion, based on Archimedes’ principle.
Accumulation corresponds to the mean annual total precipitation, which in this study is taken from Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b). It is totally turned into snow using a density of 917 kg m–3. Ablation is parameterized using the Positive-Degree-Day (PDD) semi-empirical method (Reeh, Reference Reeh1991). This method is based on an empirical relationship between the number of PDDs, computed from annual mean and July surface air temperature, and the snow and ice melting rates, which depend on the melting factors C snow and C ice, derived from observations. The number of PDDs is given by:
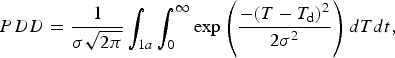 $$PDD = \displaystyle{1 \over {\sigma \sqrt {2\pi}}} \int_{1a} \int_0^\infty \exp \left( {\displaystyle{{ - {{(T - {T_{\rm d}})}^2}} \over {2{\sigma ^2}}}} \right)dTdt,$$
$$PDD = \displaystyle{1 \over {\sigma \sqrt {2\pi}}} \int_{1a} \int_0^\infty \exp \left( {\displaystyle{{ - {{(T - {T_{\rm d}})}^2}} \over {2{\sigma ^2}}}} \right)dTdt,$$
where T d is the daily temperature and σ the standard deviation of the daily temperature. This formulation allows for positive temperatures even when the average daily temperature is below the melting point. The daily temperature T d is reconstructed from annual mean and July temperatures, T Ann and T Jul, by assuming that the annual temperature cycle follows a cosine function:
In every time step during the simulation, climate input fields, namely initial downscaled surface air temperature T 0 and initial total precipitation P 0, are corrected for elevation changes:
where T cor and P cor are the corrected temperature and precipitation fields, respectively, S is the surface elevation at time step t, S 0 is the initial surface elevation λ (°C km−1) is the atmospheric lapse rate and γ (%/°C−1) is the precipitation correction factor. Note that the use of an exponential function in Eqn (4) is motivated by the saturation pressure of water vapor in the atmosphere (Clausius–Clapeyron relationship), which increases roughly exponentially with temperature (e.g. Charbit and others, Reference Charbit, Ritz and Ramstein2002).
Geothermal heat flux (GHF) at the base of the ice sheet is prescribed, taken from a present-day distribution by Shapiro and Ritzwoller (Reference Shapiro and Ritzwoller2004). Here we assume that GHF was not significantly different during MIS 6. Calving at the ice shelf front is determined by a thickness criterion. The isostatic response in GRISLI is described by the elastic lithosphere/relaxing asthenosphere method (ELRA; Le Meur and Huybrechts, Reference Le Meur and Huybrechts1996).
The equations governing ice flow, ice thickness and ice temperature evolution are discretized with the finite difference method. They are solved on a Cartesian grid (40 km × 40 km) corresponding to 241 grid points in both X and Y directions, covering the Northern Hemisphere down to 37°N and using a Lambert Equal Area geographical projection. In the vertical, the grid has 21 levels evenly spaced along the z-axis, scaled to the ice thickness, and four levels in the bedrock layer.
Two types of ice-sheet simulations, Topo1 and Topo2, were performed, differing in the initial topographies over North America (surface topography, bedrock topography and ice thickness) and prescribed climates (Section 2.2). Both topographies are constituted from the LGM Greenland ice sheet from ICE-5 G (Peltier, Reference Peltier2004) and from the PGM Eurasian ice sheet (Peyaud, Reference Peyaud2006), whose elevation reaches ~3500 m over Eurasia (Fig. 1). The extent of this PGM Eurasian ice-sheet derives from the QUEEN project (Svendsen and others, Reference Svendsen2004). However, Topo1 and Topo2 differ in the prescribed Laurentide ice sheet. While Topo1 is constituted from the Laurentide LGM ice sheet based on ICE-5G, Topo2 is constituted from a smaller Laurentide ice sheet following Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) to account for the uncertainties on the Laurentide ice-sheet extent during the PGM (Fig. 1).

Fig. 1. PGM ice thickness (~140 ka BP) prescribed in Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) K140_Topo1 (a) and K140_Topo2 (b) climate simulations. The Eurasian ice sheet corresponds to the PGM reconstruction from Peyaud (Reference Peyaud2006). Since there is no evidence about the Laurentide and the Antarctic ice sheets, we use the ICE-5G ice topography (Peltier, Reference Peltier2004) at Last Glacial Maximum (~21 ka BP) in K140_Topo1 and a smaller Laurentide ice topography, taken from Peltier (Reference Peltier2004) at 13 ka BP in K140_Topo2 to equilibrate the global ice volume.
2.2 Climate forcing
We use the PGM climate simulations carried out by Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b). The MIS 6 glacial maximum climate was simulated using the CESM 1.0.5, a fully coupled Atmosphere-Land-Ocean-Sea-Ice model (Gent and others, Reference Gent2011). The CESM coupled model was run on a finite volume grid with an horizontal resolution of ~ 1°. The atmosphere component (CAM4) has 26 vertical levels. The land model (CLM) shares the grid and horizontal resolution of the atmospheric model. The ocean model (POP2) has 60 vertical levels and is run on a grid with displaced pole over Greenland. The sea-ice model (CICE4) is fully thermodynamical and shares the grid with the ocean model. Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) provide further details about the simulations and their analysis. The two climate simulations, namely K140_Topo1 and K140_Topo2, were carried out both using the same orbital parameters (Berger and Loutre, Reference Berger and Loutre1991), CO2 (Petit and others, Reference Petit1999) and CH4 (Spahni and others, Reference Spahni2005) as for the MIS 6 glacial maximum (~140 ka), but using the two different topographies, Topo1 and Topo2 (Fig. 1).
Each climate simulation was run for 900 model years, which is sufficiently long to reach a quasi-equilibrium state in all the model components, even if a small drift still persists in the abyssal circulation (Colleoni and others, Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b). Dynamically, the PGM glacial topography induces a strengthening of the westerlies, a southward expansion of the sea-ice cover, and a southward shift of the AMOC convection sites compared with pre-industrial climate. These changes are in line with those simulated for the LGM (Brady and others, Reference Brady, Otto-Bliesner, Kay and Rosenbloom2013). The reader may refer to Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) for further details on the climate simulations. As input fields, GRISLI needs monthly surface air temperature and precipitations.These fields were averaged over the last 50 years of the climate simulations and used to force GRISLI (Fig. 2).
2.3. Ice-sheet experiments
Two reference ice-sheet experiments were carried out using K140_Topo1 and K140_Topo2 climate forcings (denoted by REF_Topo1 and REF_Topo2) and integrated for ~450 ka. Steady-state ice volume was reached as soon as ~350 ka. Both reference experiments use the physical parameters as given in Table 1. The choice of reference parameter values is based on standard values found in the ice-sheet literature.
Table 1. Overview of reference ice-sheet experiments parameters and ice-sheet sensitivity experiments

For comparison, values from literature are given. (a) Abe-Ouchi and others (Reference Abe-Ouchi, Segawa and Saito2007); (b) Alvarez-Solas and others (Reference Alvarez-Solas2011);(c) Bonelli and others (Reference Bonelli2009); (d) Charbit and others (Reference Charbit, Ritz and Ramstein2002); (e) Charbit and others (Reference Charbit, Dumas, Kageyama, Roche and Ritz2013); (f) Greve (Reference Greve2005); (g) Hellmer and others (Reference Hellmer, Kauker, Timmermann, Determann and Rae2012); (h) Marshall and others (Reference Marshall, James and Clarke2002); (i) Peyaud and others (Reference Peyaud, Ritz and Krinner2007); (j) Pfeffer and others (Reference Pfeffer, Meier and Illangasekare1991); (k) Quiquet and others (Reference Quiquet2012); (l) Ritz and others (Reference Ritz, Rommelaere and Dumas2001); (m) Rutt and others (Reference Rutt, Hagdorn, Hulton and Payne2009); (n) Tarasov and Peltier (Reference Tarasov and Peltier1999); (o) Vizcaino and others (Reference Vizcaino, Mikolajewicz, Jungclaus and Schurgers2010).
In order to investigate the sensitivity of the simulated Northern Hemisphere ice sheets to model parameters, a total of 66 univariate sensitivity experiments, summarized in Table 1, is performed. In particular, 14 model parameters were investigated, which can be assigned to five groups of experiments: impact of climate downscaling and accumulation (group A), PDD parameters (group B), parameters related to basal dragging (group C), parameters related to ice-shelf geometry (group D) and solid Earth parameters including GHF (group E). The parameter space that we chose is broad, but does not include all model parameters. However we are confident that we investigated the most sensitive parameters. All parameters were changed one by one while setting all other parameters to reference values. All sensitivity experiments were branched at 350 ka from the reference simulations REF_Topo1 and REF_Topo2, which were used as initial condition for topography, ice temperature and velocities. They were forced with K140_Topo1 and K140_Topo2 climates and integrated for 100 ka, i.e. until a steady-state ice volume was reached. In the following paragraphs, we describe in detail the settings of the experiments, also reported in Table 1.
2.3.1 Climate correction during run-time
As a first step, we investigate parameters related to climate forcing. In every time step during the simulation, climate input fields are corrected for elevation changes according to Eqns (3) and (4) by means of an atmospheric lapse rate (λ) and a precipitation correction factor (γ). Typical values of λ for paleoclimate studies conducted on the Northern Hemisphere range from 5 to 8°C km−1 (e.g. Abe-Ouchi and others, Reference Abe-Ouchi, Segawa and Saito2007; Alvarez-Solas and others, Reference Alvarez-Solas2011). We set our reference values to 5°C km−1 (mean annual, λ Ann) and 4°C km−1 (July, λ Jul) following Bonelli and others (Reference Bonelli2009), and for our sensitivity experiments, we choose lapse rates of λ Ann = 3°C km−1; λ Jul = 2°C km−1 (experiment A1), λ Ann = 6.5°C km−1; λ Jul = 5°C km−1 (experiment A2) and λ Ann = 8°C km−1; λ Jul = 6.5°C km−1 (experiment A3). For the precipitation correction factor γ, we perform experiments with γ = 0.03°C km−1, γ = 0.07°C km−1 and γ = 0.09°C km−1 covering approximately the range tested by Charbit and others (Reference Charbit, Ritz and Ramstein2002) in their study of Northern Hemisphere ice sheets during the last deglaciation (experiments A4, A5 and A6, respectively). We adopt a value of 0.05°C−1 in the reference experiments, following Charbit and others (Reference Charbit, Ritz and Ramstein2002).
2.3.2 Accumulation
In our reference simulations, all total precipitation is turned into snow with a density of 917 kg m–3. For the sensitivity experiments, we adopt another approach, which consists in scaling the total precipitation (Eqn (4)) with the length of winter calculated as fraction of days per year below a certain temperature threshold P solid(°C), denoted by FT:
The impact of setting a temperature threshold according to Eqn (5) is investigated in a set of experiments with P solid ranging from 0 to 6°C (experiments A7–A10). As a further sensitivity test to the formulation of the precipitation forcing conditions, an experiment is performed in which we instead use the snowfall field from the two PGM climate simulations (experiment A11).
2.3.3 PDD parameters
We use the PDD method (Reeh, Reference Reeh1991) to calculate ablation, which depends on:
-
(1) Melting of snow and ice: C snow is set to
 $3 \,{\rm mm}\,{{\rm d}^{ - 1}} \,^{^\circ} {{\rm C}^{ - 1}}$
and C
ice to
$3 \,{\rm mm}\,{{\rm d}^{ - 1}} \,^{^\circ} {{\rm C}^{ - 1}}$
and C
ice to
 $8\, {\rm mm}\,{{\rm d}^{ - 1}} \,^{\rm ^\circ} {{\rm C}^{ - 1}}$
in our reference simulations,
$8\, {\rm mm}\,{{\rm d}^{ - 1}} \,^{\rm ^\circ} {{\rm C}^{ - 1}}$
in our reference simulations,
 $4 \,{\rm mm}\,{{\rm d}^{ - 1}}\, ^{\rm ^\circ} {{\rm C}^{ - 1}}$
and
$4 \,{\rm mm}\,{{\rm d}^{ - 1}}\, ^{\rm ^\circ} {{\rm C}^{ - 1}}$
and
 $9 \,{\rm mm}\,{{\rm d}^{ - 1}} \,^{\rm ^\circ} {{\rm C}^{ - 1}}$
, respectively, in experiment B1, motivated by the fact that some ice-sheet modeling studies use higher values (e.g. Peyaud and others, Reference Peyaud, Ritz and Krinner2007; Quiquet and others, Reference Quiquet2012), and 2 mm d−1 °C−1 and 7 mm d−1 °C−1, respectively, in experiment B2.
$9 \,{\rm mm}\,{{\rm d}^{ - 1}} \,^{\rm ^\circ} {{\rm C}^{ - 1}}$
, respectively, in experiment B1, motivated by the fact that some ice-sheet modeling studies use higher values (e.g. Peyaud and others, Reference Peyaud, Ritz and Krinner2007; Quiquet and others, Reference Quiquet2012), and 2 mm d−1 °C−1 and 7 mm d−1 °C−1, respectively, in experiment B2. -
(2) The standard deviation of daily temperature, σ, is set to 5°C in the reference simulation (e.g. Bonelli and others, Reference Bonelli2009), while we test values ranging from 3 to 7°C (experiments B3–B6; Table 1) corresponding to the values Marshall and others (Reference Marshall, James and Clarke2002) tested in their study of the Laurentide ice sheet.
-
(3) The amount of refreezing of ice-sheet surface meltwater, csi, is set to 60% (Reeh, Reference Reeh1991). We test values of 30% in experiment B7 in order to investigate the impact of a rather small amount of refreezing, and 70% in experiment B8 as suggested by Pfeffer and others (Reference Pfeffer, Meier and Illangasekare1991).
Note that the PDD parameters we choose for the reference run are the standard parameters from Reeh (Reference Reeh1991), commonly used in ice-sheet models (e.g. Abe-Ouchi and others, Reference Abe-Ouchi, Segawa and Saito2007; Bonelli and others, Reference Bonelli2009; Rutt and others, Reference Rutt, Hagdorn, Hulton and Payne2009).
2.3.4 Fast flowing areas related parameters
Ice streams play an important role for the overall dynamics and shape of ice sheets. Two thresholds are of particular importance for the activation of ice streams in GRISLI: The hydraulic head, determined by a Darcy-type flow law, has to exceed
![]() $h_{\rm w}^* = 250\,{\rm m}$
(critical hydraulic head) and the sediment thickness, taken from a map of Laske and Masters (Reference Laske and Masters1997) (Fig. 3a), has to exceed
$h_{\rm w}^* = 250\,{\rm m}$
(critical hydraulic head) and the sediment thickness, taken from a map of Laske and Masters (Reference Laske and Masters1997) (Fig. 3a), has to exceed
![]() $h_{{\rm sed}}^* = 150\,{\rm m}$
(critical sediment thickness). Note that both thresholds,
$h_{{\rm sed}}^* = 150\,{\rm m}$
(critical sediment thickness). Note that both thresholds,
![]() $h_{{\rm sed}}^* $
and
$h_{{\rm sed}}^* $
and
![]() $h_{\rm w}^* $
, are closely connected to each other. These assumptions are in agreement with Clark and others (Reference Clark, Licciardi, MacAyeal and Jenson1996), who showed that a soft bed, i.e. wet, deformable till or sediment, is closely related to enhanced ice flow. However, no direct evidence constraining these values exists; this is why the uncertainty in the formulation and associated parameter values is large. To test the impact of the imposed thresholds, we conduct an experiment with smaller values (
$h_{\rm w}^* $
, are closely connected to each other. These assumptions are in agreement with Clark and others (Reference Clark, Licciardi, MacAyeal and Jenson1996), who showed that a soft bed, i.e. wet, deformable till or sediment, is closely related to enhanced ice flow. However, no direct evidence constraining these values exists; this is why the uncertainty in the formulation and associated parameter values is large. To test the impact of the imposed thresholds, we conduct an experiment with smaller values (
![]() $h_{{\rm sed}}^* = 30\,{\rm m}$
and
$h_{{\rm sed}}^* = 30\,{\rm m}$
and
![]() $h_{\rm w}^* = 50\,{\rm m}$
, experiment C1). Another experiment is performed that tests the impact of resolution of the sediment thickness dataset (experiment C2). Thus, a high-resolution dataset of sediment thickness covering Sweden from the Swedish Geological Survey (SGU) is merged with the global dataset from Laske and Masters (Reference Laske and Masters1997), and used as input map in GRISLI.
$h_{\rm w}^* = 50\,{\rm m}$
, experiment C1). Another experiment is performed that tests the impact of resolution of the sediment thickness dataset (experiment C2). Thus, a high-resolution dataset of sediment thickness covering Sweden from the Swedish Geological Survey (SGU) is merged with the global dataset from Laske and Masters (Reference Laske and Masters1997), and used as input map in GRISLI.

Fig. 2. Annual mean (top) and July (middle) surface air temperature (°C) and annual mean total precipitation (m a–1, bottom) averaged over the past 50 a of the CESM climate simulations described by Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b), interpolated and downscaled on the Northern Hemisphere 40 km GRISLI grid. The left and middle panels show fields for K140_Topo1 and K140_Topo2, respectively. The right panel shows the difference (for temperature, K140_Topo2 minus K140_Topo1) and ratio (for precipitation, K140_Topo2/K140_Topo1) between the two simulations.
In GRISLI, the basal drag below ice stream regions, τ
b, is proportional to basal velocitiy
![]() ${ \bar {\bf u}}$
:
${ \bar {\bf u}}$
:
where c f is the basal drag coefficient and N the effective pressure. In the work of Peyaud (Reference Peyaud2006), c f is set to 1 · 10−5 and 2 · 10−5. Alvarez-Solas and others (Reference Alvarez-Solas2011) chose larger values (1 · 10−4, 2 · 10−4, 1 · 10−3) in order to trigger Heinrich events, which are characterized by ice-sheet instabilities. In our reference experiments, c f is set to 2 · 10−5. As we do not aim to simulate very unstable ice-sheet behavior as Alvarez-Solas and others (Reference Alvarez-Solas2011), we choose to investigate the effect of a moderately larger value of c f = 3 · 10−5 in experiment C3.
2.3.5 Ice-shelf geometry
The ice-shelf geometry is affected by calving and by basal melting due to oceanic heat fluxes. Calving of ice shelves is simulated with a thickness criterion. As soon as the ice thickness at the front reaches a certain threshold H calv and the upstream ice fluxes are not enough to sustain the dynamical conditions at the front, the node is ‘cut off’. In the literature, this threshold ranges from 150 to 250 m, mostly based on observations of Antarctic ice shelves (Ritz and others, Reference Ritz, Rommelaere and Dumas2001; Peyaud and others, Reference Peyaud, Ritz and Krinner2007; Vizcaino and others, Reference Vizcaino, Mikolajewicz, Jungclaus and Schurgers2010). Therefore, in the reference experiment, H calv is set to 200 m. Sensitivity experiments test values ranging from 100 to 300 m (experiments D1–D4).
Basal melting below the ice shelves is strongly affected by the large-scale oceanic circulation (e.g. Hellmer and others, Reference Hellmer, Kauker, Timmermann, Determann and Rae2012). In our reference model setup, we use a simplified approach, in which the oceanic basal melting rate b melt depends on depth and is set to 0.2 m a–1 above 450 m and to 2.45 m a–1 below 450 m depth, similar to Peyaud and others (Reference Peyaud, Ritz and Krinner2007). This is in agreement with observations showing that below the halocline, ocean temperature rises until about 500 to 1000 meter depth, which would lead to high basal melting values. In our sensitivity experiments, we do not impose any depth limit and we prescribe high uniform basal melt values, b melt = 4 m a−1 and b melt = 10 m a−1 (experiments D5 and D6).
2.3.6 Solid earth: Isostasy and GHFs
In GRISLI, we apply the ELRA method to compute isostasy, treating the lithosphere/asthenosphere system with a visco-elastic rheology which depends on time (LeMeur and Huybrechts, Reference Le Meur and Huybrechts1996). The response time of the asthenosphere to changes in surface load is given by the characteristic relaxation time τ r, set to 3000 a in the reference simulations following Turcotte and Schubert (Reference Turcotte and Schubert2002). In Abe-Ouchi and others (Reference Abe-Ouchi, Segawa and Saito2007) and Bonelli and others (Reference Bonelli2009) τ r is set to 5000 a. Therefore, as larger values for τ r are commonly used, we test values of 5000 a and 10 000 a (experiments E1 and E2).
In our simulations we use a heterogeneous present-day GHF reconstructed by Shapiro and Ritzwoller (Reference Shapiro and Ritzwoller2004) with a horizontal resolution of 1° (Fig. 3b). Here we assume that GHF was not significantly different during the MIS6. Other ice-sheet modeling studies apply a constant value for the whole model domain, ranging from 42 mW m–2 (Ritz and others, Reference Ritz, Rommelaere and Dumas2001) to 55 mW m–2 (Abe-Ouchi and others, Reference Abe-Ouchi, Segawa and Saito2007). In order to investigate the impact of changes in GHF, the GHF values from Shapiro and Ritzwoller (2004) are uniformly reduced by 10% (experiment E3) and uniformly increased by 10% (experiment E4). In experiment E5, a more accurate, high-resolution dataset of GHF covering Sweden and Finland from Näslund and others (Reference Näslund, Jansson, Fastook, Johnson and Anderson2005) is merged with the Shapiro and Ritzwoller (Reference Shapiro and Ritzwoller2004) dataset in order to obtain a more refined GHF distribution over Scandinavia. In comparison, the average value over Sweden and Finland in Shapiro and Ritzwoller (Reference Shapiro and Ritzwoller2004) is ~8% higher relative to Näslund and others (Reference Näslund, Jansson, Fastook, Johnson and Anderson2005).
3. RESULTS
In the first part of this section we focus on the PGM reference ice-sheet simulation REF_Topo1 carried out using the standard set of model parameters reported in Table 1. The second part explores the impact of climate forcing on the simulated ice sheets dimensions. In the third part we investigate the impact of each parameter category described in Section 2.3 on the simulated ice-sheet geometry (Table 1). For convenience, ice volume is converted into meter Sea-Level Equivalent (m SLE), calculated as:
where A
oce is an estimate of the global present-day ocean area
![]() $(3.62 \times {10^8} \,{\rm k}{{\rm m}^2})$
and V
ice is the simulated ice-sheet volume. ρ
ice is the ice density set to 917 kg m–3 and ρ
w is the sea water density set to 1028 kg m–3.
$(3.62 \times {10^8} \,{\rm k}{{\rm m}^2})$
and V
ice is the simulated ice-sheet volume. ρ
ice is the ice density set to 917 kg m–3 and ρ
w is the sea water density set to 1028 kg m–3.
3.1. PGM reference simulation: REF_Topo1
The first observation is that under K140_Topo1 climate forcing, both the Laurentide and the Eurasian ice sheet remain stable. During the 450 ka of the simulation, the volume of the Eurasian ice sheet decreases from ~70 m SLE for the initial state (Peyaud, Reference Peyaud2006) to 52 m SLE. The difference between the prescribed initial and simulated final ice-sheet volume is due to differences in the climate forcing used to generate those two Eurasian ice sheets. The climate forcing used by Peyaud (Reference Peyaud2006) was based on a climate simulation of the Early Weichselian glaciation (~90 ka BP; Krinner and others Reference Krinner2004) and was modified to reconstruct the PGM Eurasian extent in agreement with Svendsen and others (Reference Svendsen2004). This forcing differs from the climates used in the present study that used the Eurasian ice-sheet topography from Peyaud (Reference Peyaud2006) and set the orbital and GHG values to the PGM. Those discrepancies with Krinner and others (Reference Krinner2004) induce changes in the large-scale circulation, leading to substantial differences in the precipitation and surface air temperature patterns over Eurasia and Siberia. The simulated Laurentide ice volume, however, increases slightly from initially 79.8 m SLE (ICE-5 G reconstruction; Peltier Reference Peltier2004) to 83.6 m SLE at the end of the simulation.
We now examine the final simulated ice thickness distribution over the Northern Hemisphere (Fig. 4a). Compared with the initial ice distribution, the largest differences over Eurasia are found in the south-west part and in the Barents Sea (Fig. 4d). Over eastern Siberia and Beringia, an ice cap grows in REF_Topo1, while this area was ice free in the initial topography. This will be further discussed in the next section. Over North America, the ice sheet thickens over the Hudson Bay area, whereas mass is lost over the central part, indicating an eastward shift of the main ice-sheet dome.

Fig. 3. Input maps used in GRISLI: (a) Sediment thickness from Laske and Masters (Reference Laske and Masters1997) and (b) GHF (mW m–2) from Shapiro and Ritzwoller (Reference Shapiro and Ritzwoller2004). Datasets were interpolated on the Northern Hemisphere 40 km GRISLI grid.
The Eurasian ice sheet in experiment REF_Topo1 does not expand beyond the initial ice-sheet margins (magenta outlines; Fig. 4a). Likewise, the extent of the simulated North American ice sheets does not exceed the extent of the initial prescribed topography. This is because the 0°C summer isotherm reaches the southward margins of both ice sheets, inhibiting their southward propagation (Fig. 2d).

Fig. 4. Simulated final ice thickness for reference simulations REF_Topo1 (a) and REF_Topo2 (b) and differences in ice thickness: REF_Topo2 minus REF_Topo1 (c), REF_Topo1 minus initial ice thickness as shown in Fig. 1a (d) and REF_Topo2 minus initial ice thickness as shown in Fig. 1b (e). The magenta outlines in (a) and (b) indicate the extent of the prescribed ice sheets for Topo1 and Topo2 (Fig. 1) used as initial conditions.
Most parts of the simulated ice-sheet base exhibit temperatures above the freezing point (Fig. 5d). Proxy-based indications of basal conditions for the MIS 6 glacial maximum are not available, but, for the LGM Eurasian and Laurentide ice sheets, Kleman and Hattestrand (Reference Kleman and Hattestrand1999) inferred the distribution of frozen- and thawed-bed conditions from the occurrence of ribbed moraines in the present-day landscape. Their study shows that large parts of northern Scandinavia must have been characterized by frozen-bed conditions during the last glacial cycle, as well as the northern part of the Laurentide ice sheet including the Canadian Arctic Archipelago. Over western Finland, our simulated basal temperature in REF_Topo1 agrees with the LGM reconstruction from Kleman and Hattestrand (Reference Kleman and Hattestrand1999), whereas most of the ice-sheet base over Scandinavia remains above the freezing point (Fig. 5d). However, since the PGM Eurasian ice sheet is substantially larger and thicker than its LGM counterpart, the comparison here is only indicative.
Over the Canadian Arctic Archipelago and south of Hudson Bay, the simulated ice-sheet base is frozen, yet the area with frozen-bed conditions is not as extensive as described by Kleman and Hattestrand (Reference Kleman and Hattestrand1999). This could result from an overestimation of the Laurentide ice thickness, already large in the prescribed initial topography. In fact, to avoid unrealistic atmospheric circulation changes in the last LGM inter-comparison exercise of the PMIP3 project, the LGM ice elevation was lowered over North America, departing from Peltier (Reference Peltier2004) ICE-5 G reconstructions (Abe-Ouchi and others, Reference Abe-Ouchi2015).

Fig. 5. Sliding velocity in m a−1 (a,b), basal temperature relative to the pressure melting point in °C (c,d) and ablation in m a−1 (e,f) of reference simulations REF_Topo1 (left column) and REF_Topo2 (right column) at the end of the simulations. The magenta outlines indicate the extent of the prescribed ice sheets for Topo1 and Topo2 (Fig. 1) used as initial conditions.
3.2 Impact of climate forcing: REF_Topo2
Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) showed that changes in Laurentide ice-sheet topography induce a shift in planetary waves, which affects the distribution of temperature and precipitation over the Northern Hemisphere high latitudes. In particular, in K140_Topo2 the strongest response occurs over North America, as a result of the lower elevation and smaller ice extent compared with K140_Topo1, and over the Nordic Seas, where air temperature increases up to 10°C and precipitation doubles compared with K140_Topo1 due to a positive geopotential height anomaly related to the shift in planetary waves (Fig. 2). In contrast, over Beringia and eastern Siberia mean annual surface air temperature decreases by up to 6°C in K140_Topo2 compared with K140_Topo1, and mean July surface air temperature decreases even more as a result of the shift in planetary waves inducing a negative geopotential height anomaly over this area. For similar reasons, in the Laptev Sea, precipitation is reduced by up to 30% in K140_Topo2 compared with K140_Topo1, while over the southern part of Eurasia, precipitation decreases as a result of the southward shift of the jet stream associated with elevation changes over North America. The reader may refer to Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) for a more complete analysis of those two climate simulations.
Although there is a strong difference between those two climate forcings, it only has a moderate impact on the Eurasian ice-sheet topography. In fact, the simulated final REF_Topo2 Eurasian ice volume is ~2 m SLE lower than in REF_Topo1 (Fig. 6). This difference in ice volume is mostly due to a thinning of the ice sheet in the southwestern part by up to 500 m in REF_Topo2 (Fig. 4c) as a result of the small summer warming occurring over this area, which is not compensated for by the large reduction in precipitation simulated over the same area. While the final simulated REF_Topo2 Laurentide ice volume is larger than its initial value (Fig. 4e), the difference in both volume and extent between Topo1 and Topo2 is preserved throughout the REF_Topo2 simulation (Fig. 4c). The REF_Topo2 Laurentide ice sheet remains less extended in the southern part than in REF_Topo1 but thickens by ~500 m over the Hudson Bay. The final Laurentide ice volume of 59.2 m SLE is 24.4 m SLE less than in the case of REF_Topo1 (Table 2). In the following, we review some observational evidence to strengthen our analysis and provide some hints to constrain the PGM Northern Hemisphere ice topography.

Fig. 6. Ice volume (m SLE) of the Eurasian (a), North American (b) and Beringia/Siberian ice sheets (c) for all preformed experiments using K140_Topo1 forcing (light colors) and K140_Topo2 forcing (dark colors) at the end of the simulations.
Table 2. Final ice volume (m SLE) for the Eurasian, Laurentide and Beringian/Siberian ice sheets for all experiments

Global ice volume is also given, by accounting for 5 m SLE for Antarctica (Ivins and James, Reference Ivins and James2005) and 2 m SLE for other small ice caps, such as in New-Zealand and Patagonia (ICE-5 G LGM). Simulations that fall in the range of global sea-level reconstructions for the PGM (Rabineau and others, Reference Rabineau2006) are indicated by bold font. Sensitivity experiments are grouped according to categories: Climate corrections (A), PDD parameters (B), Ice streams (C), Ice shelves (D) and Solid earth (E).
According to Naafs and others (Reference Naafs, Hefter and Stein2013) and Obrochta and others (Reference Obrochta2014), the PGM Laurentide ice sheet may have been smaller than during the LGM. The authors deduce this from the fact that ice rafting events in the North Atlantic, which originate from the Hudson area, were much reduced during MIS 6. Similarly, Abreu and others (Reference Abreu, Shackleton, Schonfeld, Hall and Chapman2003), investigating ice-rafted debris off the western Iberian margin, conclude that ice-rafting episodes were far less pronounced during MIS 6 than during the end of the last glacial cycle. Hiscott and others (Reference Hiscott, Aksu, Mudie and Parsons2001) analyzed sediment cores from the area north of Grand Banks and found only minor ice rafting events during MIS 6. The above described evidence clearly favor a Laurentide topography as in simulation REF_Topo2. In particular, the REF_Topo2 Laurentide ice sheet does not cover the Newfoundland area (Fig. 4b). This results from the simulated warmer climate conditions, especially during summer over Newfoundland, combined with a reduction in simulated precipitation in K140_Topo2 compared with K140_Topo1 (Fig. 2). Furthermore, the velocities of the ice stream flowing in the Hudson Strait and those flowing along the Labrador Sea coast are much lower in REF_Topo2 than in REF_Topo1 (Fig. 5a, b). This indicates that the PGM simulated climate inhibits the ice growth over this area and therefore the ice sheet is shifted slightly more inland in REF_Topo2 than in REF_Topo1. In fact, the main Laurentide ice-sheet dome is centered over the Hudson Bay in REF_Topo2, while it is slightly shifted southward in REF_Topo1 (Fig. 4a, b). Furthermore, the main Laurentide ice-sheet dome grows along a northwest-southeast axis in REF_Topo2, while in REF_Topo1, the ice-sheet growth is more zonal.
In East Siberia, observations indicate that this area was extensively glaciated during MIS 6, while this was not the case during the LGM. Barr and Solomina (Reference Barr and Solomina2014) reported that during MIS 6, the glaciation over the Kamchatka peninsula was more extensive and likely covered the entire peninsula. Moreover, ice-rafted debris was found in the North Pacific originating from coastal Alaska, coastal Siberia and the Kamchatka peninsula (St John and Krissek, Reference St John and Krissek1999; Nürnberg and others, Reference Nürnberg, Dethleff, Tiedemann, Kaiser and Gorbarenko2011). According to Nürnberg and others (Reference Nürnberg, Dethleff, Tiedemann, Kaiser and Gorbarenko2011), ice-rafted debris accumulation in the Okhotsk Sea was significantly higher during the PGM compared with the LGM. Our simulations show that the glaciated area over East Siberia in REF_Topo2 is much more extensive than in REF_Topo1 (Fig. 4a, b). This results from much colder surface air temperatures simulated over Beringia in K140_Topo2 (Fig. 2), which can be attributed to the development of a negative geopotential height anomaly allowing cold Arctic air to penetrate into this area, while at the same time precipitation does not change significantly between the two climate simulations (Colleoni and others, Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b).
Niessen and others (Reference Niessen2013) and Dove and others (Reference Dove, Polyak and Coakley2014) recently identified marine glaciogenic landforms at ~1 km depth in the East Siberian Sea, and proposed that this area might have been covered by an ice cap that expanded over the emerged continental shelf, promoting the growth of an ice shelf in the Chukchi Sea. In both simulations, REF_Topo1 and REF_Topo2, an ice cap grows over Beringia, reaching thicknesses of up to 2500 m (Fig. 4a, b). This is due to the initial topography used in the climate simulations, in which this area emerges due to the sea-level drop. As a consequence of the simulated cold climate, a perennial snow cover accumulates over this emerged area (Colleoni and others, Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b; their Fig. 8). In addition, the snow cover in this area is particularly thick, which further strengthens the snow albedo feedback. Therefore these conditions are favorable to the growth of an ice sheet in GRISLI. Due to a much larger extent, the total ice volume over Beringia and East Siberia is around twice as large in REF_Topo2 as in REF_Topo1 (23.8 m SLE vs 10.6 m SLE; Fig. 6c; Table 2). Colleoni and others (Reference Colleoni, Kirchner, Niessen, Quiquet and Liakka2016a) showed that this East Siberian perennial snow cover is a robust feature of the PGM climate compared with the LGM and is not climate model dependent.
Note that the northern part of Alaska remains ice free in both simulations. The reason for this is relatively warm air masses over Alaska (Fig. 2), which originate from the south and could not be blocked on their way north due to rather low simulated Cordillerian and Laurentide ice sheets (e.g. Löfverström and others, Reference Löfverström, Liakka and Kleman2015).
3.3. Impact of model parameters
In the previous section, we presented ice-sheet simulations performed with model parameter values which we believe are standard. However, to increase the reliability of our results, a range of sensitivity experiments was performed. As described in Section 2.3, we branched all sensitivity experiments from REF_Topo1 and REF_Topo2 after 350 ka of simulation. We assess the impact of each parameter in terms of ice volume, which is synthesized in Figure 6 and Table 2 for the Eurasian, Laurentide and Beringian/Siberian ice sheets for all sensitivity experiments using K140_Topo1 and K140_Topo2 climate forcing. In the following, we focus particularly on the parameters that lead to significant changes in ice volume, defined here as a deviation of 5% from the reference simulations.
Regarding climate correction parameters (group A), the model reacts particularly sensitively to changes in lapse rate and accumulation treatment. Using large lapse rates of λ Ann = 8°C km−1;λ Jul = 6.5°C km−1 (experiment A3) almost leads to the complete retreat of the western Eurasian ice sheet, in particular under K140_Topo2 climate forcing due to the simulated warm temperature over this area (Fig. 2). Compared with the reference experiments, the Eurasian ice volume reduces by 5.5 m SLE in case of K140_Topo1 forcing, and by 14.4 m SLE in case of K140_Topo2 forcing (Fig. 6; Table 2), which shows that this choice of lapse rates is not suitable to maintain an Eurasian ice sheet as large as reconstructed by Svendsen and others (Reference Svendsen2004) and Peyaud (Reference Peyaud2006). In contrast, the Laurentide ice sheet gains volume using high lapse rates, by 3.3 and 2.7 m SLE, respectively, for K140_Topo1 and K140_Topo2 climate forcing. Increasing lapse rates leads to higher surface air temperature and thus higher ablation than in the reference experiments. This induces an increase in vertical heat diffusion, leading to a warmer ice-sheet base, which in turn causes higher sliding velocities. As a consequence of the warmer surface, accumulation is higher than in the reference experiments due to the precipitation correction parametrization adopted in the GRISLI model, based on Charbit and others (Reference Charbit, Ritz and Ramstein2002). The warmer base and the higher accumulation partly compensate each other, and lead to an opposite response of Eurasian and Laurentide ice sheets to a larger lapse rate value.
Using the simulated snowfall field instead of the total precipitation (experiment A11) strongly reduces the Eurasian and Laurentide ice volumes by ~3.5 and 5.2 m SLE, respectively, compared with REF_Topo1 (Fig. 6; Table 2). A similar response occurs under K140_Topo2 climate forcing. This is because the simulated total precipitation is constituted of the liquid precipitation and the snowfall. Providing the snowfall field only to GRISLI reduces the amount of accumulation occurring over the ice sheets. When accounting for the total precipitation input, the runtime temperature correction resulting from changes in ice-sheet elevation can lead to cooler conditions, mostly occurring along the ice-sheet margins, where in the initial climate forcing, precipitation was only liquid.
Changes in PDD parameters (group B) have a moderate impact on the simulated ice volumes, as ablation is confined to the margins of the ice sheets (Fig. 5e, f). Compared with the reference experiment REF_Topo1, using higher melting rates for ice (C ice) and snow (C snow) (experiment B1) decreases the Eurasian and Laurentide ice volumes by 1.4 and 4 m SLE, respectively, relative to REF_Topo1 (Fig. 6; Table 2). Coherently, using lower melting rate coefficients (experiment B2) increases the Eurasian and Laurentide ice volumes by 1.9 and 2 m SLE, respectively, relative to REF_Topo1. Decreasing the standard deviation of surface air temperature, σ, to 3°C (experiment B3), leads to a reduction in ablation and therefore to an increase in Eurasian and Laurentide ice volume of ~2.2 m SLE and 3.1 m SLE compared with REF_Topo1. Using K140_Topo2 climate forcing leads to similar results as using K140_Topo1 climate forcing.
The strongest model response occurs when perturbing ice streams related parameters (group C). Using lower thresholds for the sediment thickness and hydraulic head (note that both parameters are connected; Section 2.3), as done in experiment C1, leads to an expansion of the fast-flow areas (i.e. an expansion of areas treated with the SSA; Section 2.1) compared with the reference simulations. This increases basal velocities in areas treated with SIA only in the reference simulations. As a result, the ice sheets lose mass and become flatter than in the reference simulations. These changes in ice volume are more pronounced for the Laurentide ice sheet (reduction by 12.1 m SLE compared with REF_Topo1) than for the Eurasian ice sheet (reduction by 3.5 m SLE compared with REF_Topo1) (Fig. 6; Table 2). This is because in the reference simulations, the Laurentide ice sheet exhibits only a few ice streams compared with the Eurasian ice sheet (Fig. 5a, b). Consequently, the Laurentide ice sheet is more sensitive than the Eurasian ice sheet to an increase in the area treated with the SSA.
Using a larger basal drag coefficient c f compared with the reference value, as is done in experiment C3, substantially reduces the velocities at the base of the ice sheet in ice-stream areas, which are located mostly where the sediment layer is thick (Fig. 3a). Compared with REF_Topo1, the Eurasian and Laurentide ice sheets consequently thicken and gain mass (increase by 4 and 7 m SLE, respectively). Similarly, using K140_Topo2 climate forcing the Eurasian and Laurentide ice volume increases by 3.7 and 3.8 m SLE, respectively, compared with REF_Topo2.
The model is relatively insensitive to changes in ice-shelf geometry related parameters (group D) or changes in solid earth parameters (group E). In our simulations, most of the ice sheets are grounded (not shown; see Colleoni and others, Reference Colleoni, Wekerle and Masina2014). Therefore, the overall simulated ice volume is not particularly sensitive to changes in the calving front thickness and basal melt rate below the ice shelves (Fig. 6; Table 2). Changes in GHF have a relatively small impact on Eurasian ice volume, as large parts of the ice-sheet base are already at the pressure melting point due to relatively warm climate and the large thickness of the ice sheets (Fig. 5c, d). Similarly, the model results are insensitive to changes in parameters related to isostasy, as we perform steady-state sensitivity experiments that are branched from an already spun-up ice-sheet topography, already in isostatic equilibrium.
Over East Siberia, the ice cap exhibits a similar dynamical behavior to changes in model parameters as the Laurentide and the Eurasian ice sheets (Fig. 6c). However, the sensitivity of the East Siberian ice cap to changes in model parameters is larger compared with the responses of the Laurentide and Eurasian ice sheets. This is because the ice cap is smaller than those ice sheets and is therefore more sensitive to changes in air surface temperature and precipitation than the two larger ice sheets (group A and B). Consequently, while in the case of the Laurentide and Eurasian ice sheets the upper and lower bounds in ice volume are given by simulations of group C, i.e. basal drag and ice stream area related simulations, the upper and lower bounds are given by group A, i.e. climate forcing related simulations. In addition, the East Siberian ice cap is also sensitive to changes in ice-shelf basal melting and calving criteria (group D) under K140_Topo2 climate conditions because some ice shelves develop in this area (not shown), which is not the case under K140_Topo1 climate conditions. Because this ice cap develops from an ice-free topography, it is in general more sensitive to isostasy, which induces a negative elevation feedback on the surface air temperature and precipitation correction during the simulation, and to GHF variations (group E). The maximum simulated ice volume of the East Siberian ice cap amounts to 14.9 m SLE and 27.8 m SLE in experiment B3, whereas the minimum amounts to 8.2 m SLE and 18.8 m SLE in experiment A11 under K140_Topo1 and K140_Topo2 climate forcing, respectively.
4. DISCUSSION
We performed an ensemble of steady-state ice-sheet experiments simulating the MIS 6 glacial maximum Northern Hemisphere ice-sheet topography, forced by two PGM climate simulations, and based on two different Northern Hemisphere PGM ice-sheet topographies (Topo1 and Topo2; Colleoni and others, Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b). To understand whether those ice-sheet topographies were viable or not in an ice-sheet model, the parameter space of GRISLI was systematically tested by means of univariate sensitivity experiments. The simulations described in the previous sections show that under K140_Topo1 climate conditions, Topo1 is viable; however, the dimension of the Laurentide ice sheet is particularly large, which could lead to overestimated volume and extent, even in the framework of the penultimate glaciation. Under K140_Topo2 climate conditions, which are warmer than the K140_Topo1 conditions, the dimensions of the Laurentide and Eurasian ice sheets seem more reasonable. Also, a large ice cap develops over East Siberia, which is not in contradiction with the geological evidence. In the following discussion, we put our results in the context of global PGM ice volume. Then, we discuss the impact of the initialization method and the effect of steady-state simulations on the ice-sheets geometry.
4.1 Global PGM ice volume
Reconstructing the global ice topography is a difficult exercise when only few data are available to constrain the individual ice sheets for a given time period. In Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b), to account for the uncertainty on ice topography, two different Northern Hemisphere ice-sheet topographies were prescribed (Section 2.2). Both topographies include the PGM Eurasian ice sheet from Peyaud (Reference Peyaud2006) and the LGM Greenland and Antarctic ice sheets. However, they differ over North America where the LGM Laurentide ice topography was imposed in Topo1, while a substantially smaller Laurentide ice topography corresponding to 13 ka BP was prescribed in Topo2. The distinction in the Laurentide ice-sheet topographies derives from the fact that no geological evidence for a larger glaciation than the LGM over this area has been found so far (Dyke and others, Reference Dyke2002). This implies that previous glaciations over North America could have been smaller than or no larger than the LGM Laurentide ice sheet. The reader may refer to Colleoni and others (Reference Colleoni, Wekerle and Masina2014) and Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) for a more detailed discussion about the Laurentide topography. In addition, Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) assume that Antarctica and Greenland during MIS 6 glacial maximum were not substantially different than during the LGM, which is supported by De Boer and others (Reference De Boer, Lourens and Van De Wal2014) for Antarctica.
Both initial global ice-sheet topographies, Topo1 and Topo2, lead to an ice volume of 167 m SLE when accounting for the LGM Laurentide ice sheet and of 123 m SLE when reducing the Laurentide ice volume (Table 3). According to past sea-level data, the MIS 6 glacial maximum sea-level drop ranges between 92 m and ~150 m (Rabineau and others, Reference Rabineau2006). This means that the global ice-sheet topography prescribed in K140_Topo1 is out of the range of past observations. On the contrary, the ice-sheet topography prescribed in K140_Topo2 stays in the range of the observations. If we now account for the Northern Hemisphere ice volumes from the two control simulations carried out in the present study, it leads to a simulated global volume of 162.2 m SLE in the case of Topo1 and 149.7 m SLE in the case of Topo2 (Table 3). Only REF_Topo2 is in the range of past sea-level reconstructions. Based on this comparison, most sensitivity experiments using K140_Topo1 forcing fall out of the range of global sea-level reconstructions, except for experiments A11 and C1 (Fig. 7; Table 2). Conversely, several experiments using K140_Topo2 forcing match the sea-level reconstruction. In the case of K140_Topo2 forcing the lower bound in Northern Hemisphere ice volume reaches 124.3 m SLE in experiment C1, which, accounting for the other ice sheets, would lead to a global ice volume of 131.3 m SLE, whereas the upper bound in Northern Hemisphere ice volume reaches ~152 m SLE in experiments B3 and C1. Figure 8 shows three examples of final ice-sheet topographies that match the sea-level reconstruction.

Fig. 7. Ice volume (m SLE) of the Northern Hemisphere (a) and North American + Eurasian ice sheets (excluding the Siberian ice cap) (b) for experiments using K140_Topo1 forcing (light colors) and K140_Topo2 forcing (dark colors) at the end of the simulations. Black solid and dashed lines denote the lower and upper limits, respectively, of global sea-level reconstructions for MIS 6 by Rabineau and others (Reference Rabineau2006).

Fig. 8. Simulated final ice thickness for sensitivity experiments A11 (a), B1 (b) and C1 (c) using K140_Topo2 climate forcing. The magenta outline indicates the extent of the initial ice sheets prescribed Topo2 (Fig. 1b).
Table 3. Ice volume comparison of various PGM reconstructions departing from present-day ice-sheet volume

K140_Topo1 corresponds to the climate simulation from Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b) in which the Late Saalian ice topography from Peyaud (Reference Peyaud2006) and the ICE-5G Laurentide ice sheet from Peltier (Reference Peltier2004) were prescribed, whereas in K140_Topo2 a smaller Laurentide ice sheet (13 ka, Peltier, Reference Peltier2004) was prescribed; REF_Topo1 and REF_Topo2 (GRISLI) take into account the modeled reference Northern Hemisphere ice sheets obtained in the present study using K140_Topo1 and K140_Topo2 climate forcing, respectively. For comparison, ICE-5 G ice-sheet volume is also shown. AIS stands for Antarctic ice sheet (estimated ice volume from Ivins (Reference Ivins and James2005)), GIS for Greenland ice sheet (from ICE-5 G LGM model) and Other corresponds to the small ice caps, such as over New-Zealand and Patagonia (ICE-5G LGM).
Our simulations cannot directly provide clues to reconstruct a global ice topography because we forced GRISLI with two simulated climates, in which idealized PGM ice topographies were prescribed. However, it suggests that a relatively large Eurasian ice sheet (~50 m SLE), but smaller than that suggested by Peyaud (Reference Peyaud2006), in combination with a relatively small Laurentide ice sheet (~60 m SLE) compared with LGM conditions as obtained in our Topo2 simulations, is reasonable in terms of global water budget. Moreover, as described by Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b), a small Laurentide ice sheet is necessary to generate a shift in planetary waves sufficient to induce a cooling over East Siberia and Alaska in order to match with both sea surface temperature proxies and ice-sheet dynamics evidence.
4.2 Initialization of simulations
In our study, the MIS 6 Eurasian ice sheet equilibrates at a total ice volume of 52 m SLE for REF_Topo1 and 50.3 m SLE for REF_Topo2. In the case of REF_Topo1, this is 26% less than in the original reconstruction from Peyaud (Reference Peyaud2006). There is no direct evidence of the PGM Eurasian ice volume, and the only two reconstructions that existed before the present study are those of Peyaud (Reference Peyaud2006) and Lambeck and others (Reference Lambeck2006). The latter study corresponds to a simulated ice volume of ~60 m SLE, which is close to what we obtain in the present study. Lambeck and others (Reference Lambeck2006) used an idealized ice-sheet model in combination with a post-glacial rebound model to reconstruct the Late-Saalian–Weichselian evolution of the Eurasian ice sheet. However, the fact that we use an ice-sheet model forced by coupled climate simulations of the PGM is a clear improvement with respect to the works by Peyaud (Reference Peyaud2006) and Lambeck and others (Reference Lambeck2006). For the PGM Laurentide ice sheet however, no estimates of ice volume exist. Nonetheless given the large ice volumes simulated in the present study, there are some aspects related to the initialization of our simulations and the assumption of steady state that need to be considered.
A continental-size ice sheet is characterized by a long-term memory of climate conditions, which affects the thermo-mechanical response on a long time-scale due to diffusion and advection of heat from the ice-sheet surface to the base, linked with mechanical deformation within the ice sheet itself. As a consequence, performing a realistic simulation of the ice-sheet evolution during a period of time requires knowledge of both the past and the contemporaneous climate conditions. This fact underlines the need to properly spin-up the ice-sheet model to obtain a realistic representation of the vertical temperature distribution within the modeled ice sheet.
To initialize the thermodynamical state of an ice sheet, two methods are commonly used, namely transient simulations driven by paleoclimate reconstructions of temperature and precipitation through time, or alternatively steady-state simulations forced by simulated climate conditions at a given time (Rogozhina and others, Reference Rogozhina, Martinec, Hagedoorn, Thomas and Fleming2011; and references therein). In addition, when starting a steady-state simulation, it is possible to either use a prescribed ice-sheet topography or to start from an ice-free topography (relaxed from isostasy). Rogozhina and others (Reference Rogozhina, Martinec, Hagedoorn, Thomas and Fleming2011) show that starting from an ice-covered topography shortens the spin-up time required to bring temperatures and velocities to equilibrium. However, glacial climate forcing bears low precipitation rates, which implies that simulations have to be longer before reaching steady state, thus leading to an underestimation of final ice volume.
In this study, we initialized our simulations starting from an ice-covered topography and ran those experiments for 450 ka. To understand what could have been the impact of initializing from an ice-free topography, we carried out an additional experiment starting from the present-day ice-free topography and forced by K140_Topo1 climate. Both experiments, i.e. starting from an ice-sheet topography and from an ice-free topography reach equilibrium after ~100 ka and the final ice-sheet extent and volume is similar (not shown). However, compared with the initial Eurasian ice volume from Peyaud (Reference Peyaud2006), the ice volume is ~18 m SLE smaller and is closer to the Lambeck and others (Reference Lambeck2006) reconstruction.
In the case of transient simulations, precipitation before reaching the glacial maximum could potentially be larger because of warmer climate conditions. In this case, ablation that would occur because of high temperatures would be balanced by large precipitation rates and would not necessarily imply a larger or lower ice volume. Colleoni (Reference Colleoni2009) showed that under warmer climate conditions, i.e. 150 ka BP, the surface mass balance of the PGM Eurasian ice sheet would still be positive and not much lower than during the full PGM. As stressed by Rogozhina and others (Reference Rogozhina, Martinec, Hagedoorn, Thomas and Fleming2011), running a long simulation prescribing very low precipitation from the beginning might lead to a smaller ice volume than running it transiently for a shorter time period but starting from interglacial wet climate conditions and finishing with glacial dry climate conditions.
5. CONCLUSIONS
The overall aim of this study was to investigate the geometry of the Northern Hemisphere ice sheets during the PGM (~140 ka BP). Our results show that:
When using a climate forcing accounting for a large Laurentide ice sheet (Topo1), the Eurasian ice-sheet volume decreases by ~20 m SLE from the reconstruction of Peyaud (Reference Peyaud2006), whereas the Laurentide ice sheet does not change significantly. Prescribing a smaller Laurentide ice sheet (Topo2) in the climate simulations reduces both the Laurentide and the Eurasian ice volume by ~20 m SLE compared with the initial prescribed topography, due to simulated warmer climate conditions.
The simulated Eurasian ice volume appears to be relatively insensitive to the changes induced by the atmospheric circulation when lowering the Laurentide ice-sheet elevation, whereas under the warmest simulated PGM climate conditions the Laurentide ice sheet remains small in the ice-sheet simulations. This means that once the Eurasian ice sheet has reached a significant dimension, it limits the growth of the Laurentide ice sheet by shifting the planetary waves and inducing local changes in temperatures and precipitations. This is supported by the findings from Beghin and others (Reference Beghin, Charbit, Dumas, Kageyama and Ritz2015) and Liakka and others (Reference Liakka, Löfverström and Colleoni2015).
In both simulations, an ice sheet develops over Beringia and East Siberia, which is even more extensive when using K140_Topo2. This is supported by evidence recently found on the Arctic ocean floor (Niessen and others, Reference Niessen2013; Dove and others, Reference Dove, Polyak and Coakley2014). This East Siberian ice cap is a distinctive feature of the penultimate glaciation because the evidence also indicates that this area remained mostly ice free during the LGM.
Finally, a comparison with proxies such as ice rafted debris in the North Atlantic and North Pacific suggests that experiments using climate forcing which accounts for a small Laurentide ice sheet are more realistic than when prescribing a large Laurentide ice sheet in the climate model. Furthermore, we find that Topo2 ice-sheet experiments are in better agreement with the global water budget for this time period.
In order to better constrain the PGM ice volume, it is necessary to perform a transient coupled ice-sheet-climate simulation. Since there is little evidence of the PGM glaciation remains, it will be highly difficult to validate the evolution of the ice-sheet topography over the penultimate glacial cycle. However, following the approach by Colleoni and others (Reference Colleoni, Wekerle, Näslund, Brandefelt and Masina2016b), testing different ice-sheet combinations in a coupled climate model and comparing the simulated climate dynamics with multi-proxy compilations, should help to reduce the number of viable ice-sheet topographies for the PGM.
ACKNOWLEDGEMENTS
Financial support for this study was provided by the Swedish Nuclear Fuel and Waste Management Company (SKB) and by the Finnish Waste Management Company Posiva. We acknowledge the numerical support of CMCC Foundation. We thank Catherine Ritz for providing the GRISLI code and Vincent Peyaud for providing the initial ice topography used in this study. We acknowledge Nina Kirchner, Mike Thorne, Allan Hedin and Patrick Applegate for helpful discussions.












