1. INTRODUCTION
Over the past few decades, marine-ending (or tidewater) glaciers around the world have lost mass at dramatic rates (e.g. Meier and Post, Reference Meier and Post1987; Rignot and Kanagaratnam, Reference Rignot and Kanagaratnam2006; Pritchard and others, Reference Pritchard, Arthern, Vaughan and Edwards2009; Shepherd and others, Reference Shepherd2012). This widespread accelerated loss of ice into the ocean is attributed to an increase in rate of the interrelated processes of surface melting, iceberg calving and submarine melting at the glacier terminus. Together these processes cause glaciers to thin, accelerate and retreat (Meier and Post, Reference Meier and Post1987; Luckman and others, Reference Luckman, Murray, de Lange and Hanna2006; Howat and others, Reference Howat, Joughin and Scambos2007; van den Broeke and others, Reference van den Broeke2009). Difficulty in understanding processes occurring along this critical ice/ocean boundary has been identified as the major factor limiting the accuracy of future sea-level rise predictions (Lemke and others, Reference Lemke and Solomon2007; Straneo and others, Reference Straneo2013). Currently, roughly one-third of sea-level rise is caused by ice loss from mountain glaciers and ice caps (Lemke and others, Reference Lemke and Solomon2007; Gardner and others, Reference Gardner2013), however in the coming century, ice losses from these glaciers are expected to be the dominant cause of sea-level rise despite the much larger volume of ice contained in the major ice sheets (Meier and others, Reference Meier2007; Radić and Hock, Reference Radić and Hock2011). Thus, the study of processes occurring along the critical ice/ocean boundary of tidewater glaciers, which can lose ice at an exceptional rate (e.g. Cogley, Reference Cogley2009) has broad scientific and societal relevance (e.g. Joughin and others, Reference Joughin, Smith and Medley2014; Rignot and others, Reference Rignot, Mouginot, Morlinghem, Seroussi and Scheuchi2014).
One key characteristic of the ice/ocean boundary is the water depth, due to its strong correlation with rates of mass loss (e.g. Brown and others, Reference Brown, Meier and Post1982; Meier and Post, Reference Meier and Post1987; Alley, Reference Alley1991; Pelto and Warren, Reference Pelto and Warren1991; Jenkins, Reference Jenkins2011; Motyka and others, Reference Motyka, Dryer, Amundson, Truffer and Fahnestock2013). Glacially produced sediment transported to the ice/ocean boundary affects the water depth, and thus glacier mass balance and stability, by forming shoals that buttress the glacier, reducing buoyancy at the ice front and decreasing the surface area available for submarine melting. In fjords adjacent to the termini of temperate glaciers, rates of sediment accumulation are among the highest recorded; they can exceed 10 m a−1 at the ice front and ~1 m a−1 kilometers down the fjord (Cowan and Powell, Reference Cowan, Powell, Anderson and Ashley1991; Jaeger and Nittrouer, Reference Jaeger and Nittrouer1999). The importance of the interaction between glaciers and the sediment they erode has long been recognized, as sediment shoals enable tidewater glaciers to advance into deep water (e.g. Meier and Post, Reference Meier and Post1987; Nick and others, Reference Nick, van der Veen and Oerlemans2007; Goff and others, 2012). This interaction, however, has received relatively little focused attention, due in large part to the dearth of field data from the ice/ocean boundary of tidewater glaciers, where conditions are unfavorable for direct observations below the water line. The rapid accumulation of sediment and its variation in space and time merit close attention as perhaps, the only known negative feedback that can slow or stop the demise of a marine-ending ice mass retreating into deepening water (Alley and others, Reference Alley, Anandakrishnan, Dupont, Parizek and Pollard2007; Schoof, Reference Schoof2007).
In addition to affecting the mass balance and stability of tidewater glaciers, sediments discharged by these glaciers frequently accumulate in fjord basins and on continental shelves, where they form valuable sedimentary records of glacier fluctuations caused by changes in climate, erosion and sediment transfer (e.g. Syvitski, Reference Syvitski1989; Koppes and Hallet, Reference Koppes and Hallet2002; Berger and others, Reference Berger2008; Cowan and others, Reference Cowan2010; Willems and others, Reference Willems, Powell, Cowan and Jaeger2011). Our ability to interpret past Earth conditions from these sediment records relies on reliably connecting fjord sediment deposits to the glacial and climatic conditions under which they formed, and to changes in these conditions. However, the potential subglacial storage of substantial volumes of sediments and their subsequent evacuation, highlighted in recent studies of Alaskan glaciers (e.g. Motyka and others, Reference Motyka, Truffer, Kuriger and Bucki2006; Cowan and others, Reference Cowan2010), complicate inferences made from fjord sediments about rates of sediment production by glacier erosion (e.g. Koppes and Hallet, Reference Koppes and Hallet2002). Improving our understanding of the glacial and environmental data archived in glaciogenic sediments, as well as assessing the potential contribution of stored sediments to the sediment yield of glaciers, requires studies in settings for which the glacier behavior is known, the chronology of sedimentation is well constrained and the sediments can be studied.
Herein, we focus on how the sediment yield of Columbia Glacier, Alaska, has varied during its well documented 30 a retreat, and consider whether this variation is related to changes in glacier dynamics. This work leverages the unique set of observations at Columbia Glacier over 3 decades of dynamic retreat, reported in the multi-chapter U.S. Geological Survey Professional Paper 1258, and a series of journal articles (Humphrey and others, Reference Humphrey, Kamb and Fahnestock1993; Kamb and others, Reference Kamb, Engelhardt and Fahnestock1994; Meier and others, Reference Meier1994; Krimmel, Reference Krimmel2001; O'Neel and others, Reference O'Neel, Pfeffer, Krimmel and Meier2005, Reference O'Neel, Marshall, McNamara and Pfeffer2007; Pfeffer, Reference Pfeffer2007; Walter and others, Reference Walter2010; Post and others, Reference Post, O'Neel, Motyka and Streveler2011; Rasmussen and others, Reference Rasmussen, Conway, Krimmel and Hock2011; McNabb and others, Reference McNabb2012; Rignot and others, Reference Rignot, Mouginot, Larsen, Gim and Kirchner2013). We use seismic surveys and bathymetric measurements made in 2011 and diverse glaciological data to: (1) determine the volume and seismic architecture of sediment delivered by Columbia Glacier during its retreat; (2) develop a physically-based numerical model to study the formation of the sediment packages in Columbia Fjord as influenced by the glacier retreat, sediment-flux history and patterns of sediment deposition and redistribution near the ice front; (3) interpret the modeled sediment-flux history in light of the documented glacier-dynamics history.
2. COLUMBIA GLACIER
Columbia Glacier is a temperate tidewater glacier located in south-central Alaska's Prince William Sound region (61.1°N, 147.1°W). The glacier is presently 49 km long and is composed of two main calving branches that together cover an area of ~900 km2 and range in elevation from 0 to 3050 m a.s.l. (Fig. 1a). The climate of coastal Alaska is cool and wet; the annual average temperature is 3.9°C, and rainfall and snowfall are ~1.5 m a−1 and ~1 m w.e. a−1, respectively, as measured at sea level in Valdez, Alaska, ~35 km east of the glacier (U.S. National Weather Service). Modeled rainfall and snowfall at 1000 m elevation total ~5.5 m w.e. a−1 (Rasmussen and others, Reference Rasmussen, Conway, Krimmel and Hock2011); the heavy precipitation (Weingartner and others, Reference Weingartner, Danielson and Royer2005; O'Neel and others, Reference O'Neel2015) sustains the extensive glaciers in the region, many of which approach or reach sea level. In the early 1980s, after roughly two centuries of stability (Nick and others, Reference Nick, van der Veen and Oerlemans2007), Columbia Glacier entered a phase of rapid retreat (Meier and others, Reference Meier, Rasmussen and Miller1985a, Reference Meier, Rasmussen, Krimmel, Olsen and Frankb). Thinning at the terminus forced a dynamic instability (Pfeffer, Reference Pfeffer2007) that resulted in accelerated surface lowering, retreat and a permanent loss of contact with the stabilizing moraine shoal (Meier and Post, Reference Meier and Post1987; Post and others, Reference Post, O'Neel, Motyka and Streveler2011) (Fig. 1b). The retreat accelerated until the early 1990s, after which it slowed for two periods between 1994–1997 and 2000–2006 (Meier and Post, Reference Meier and Post1987; Pfeffer and others, Reference Pfeffer, Cohn and Meier2000; O'Neel and others, Reference O'Neel, Pfeffer, Krimmel and Meier2005), and has accelerated again since September 2006 (Fig. 1c). Since 1980, the glacier has lost half of its volume and thickness (McNabb and others, Reference McNabb2012), the terminus has retreated 23 km at an average rate of ~0.7 km a−1, and a >300 m deep fjord now replaces the lower portion of the ~1 km thick glacier. In the next few decades, Columbia Glacier is expected to retreat another ~20 km across a major subglacial overdeepening until the glacier bed rises above sea level (Mayo and others, Reference Mayo, Trabant, March and Haeberli1979; Rignot and others, Reference Rignot, Mouginot, Larsen, Gim and Kirchner2013). Contemporary ice discharge from Columbia Glacier exceeds that of any other Alaskan glacier and accounts for ~6% of the sea-level rise contribution from Alaskan glaciers during the period 1962–2006 (Berthier and others, Reference Berthier, Schiefer, Clarke, Menounos and Remy2010). Because mass loss from all Alaskan glaciers accounts for 20% of global ice loss (Gardner and others, Reference Gardner2013), Columbia alone accounts for ~1% of global ice mass loss since the 1960s.

Fig. 1. (a) Bathymetry of Columbia Fjord, collected by NOAA (Noll, Reference Noll2005) and this study, is shown in graded blue. Columbia Glacier annual terminus positions during the retreat from 1980 to 2011 and, at the southern end, the stable terminus position of Columbia Glacier in 1954 (white lines). Inset shows the location of Columbia Fjord in northeast Prince William Sound, AK. (b) Retreat history of Columbia Glacier (black) with smoothing (red), which was used to calculate the retreat rate, shown in (c).
Columbia Glacier has been surveyed in detail since 1976 by aerial photography at sub-annual intervals, and since 2004 with approximately daily time-lapse photography (Krimmel, Reference Krimmel2001; O'Neel and others, Reference O'Neel, Pfeffer, Krimmel and Meier2005). This photographic record documents the recent retreat of Columbia Glacier and provides a detailed history of the glacier terminus positions, ice velocities and rates of thinning (Fig. 1b; Krimmel, Reference Krimmel2001). The extensive existing data have been used to develop the time history of mass balance from Columbia Glacier (Rasmussen and others, Reference Rasmussen, Conway, Krimmel and Hock2011), which was used in conjunction with glacier velocity data to calculate ice thickness and bed topography over the entire glacier area (McNabb and others, Reference McNabb2012). Early during its retreat in 1987, two boreholes were drilled to the bed of Columbia Glacier to probe basal conditions (Humphrey and others, Reference Humphrey, Kamb and Fahnestock1993; Meier and others, Reference Meier1994). These data, together with bathymetric measurements in 1997 (Krimmel, Reference Krimmel2001), multibeam mapping in 2005 (Noll, Reference Noll2005) and our bathymetric and seismic measurements in 2011, constrain the evolution of the fjord seabed as sediments accumulated. Whereas the retreat history and dynamics of the glacier have been documented in detail, and a sediment shoal has long been inferred to play a central role in the stability of this glacier (e.g. Meier and Post, Reference Meier and Post1987; Nick and others, Reference Nick, van der Veen and Oerlemans2007), essentially no data were available concerning the sediments produced by Columbia Glacier prior to the research presented herein.
3. OBSERVATIONAL METHODS AND ANALYSES
3.1. Fjord seabed and sediment datasets
In September 2011, during rare nearly iceberg-free conditions, we collected bathymetric and sedimentologic measurements throughout the entire Columbia Fjord, including a previously uncharted area within 7 km of the 2011 glacier terminus (Fig. 2). Seismic-reflection profiles of the fjord were acquired using a 750 Hz bubble pulser, six kasten cores were collected in a transect extending nearly to the ice front and bathymetric measurements were obtained throughout the fjord.

Fig. 2. Location of seismic profiles (black dotted lines), and approximate terminus position in 1997 (white dashed curve). Seismic lines (red) shown in next figure: longitudinal profile from A to A’, close to the 1980 moraine, in Figure 3a, and transverse profile from B to B’ in Figure 3b. Locations of boreholes drilled in 1987 through the approximately kilometer-thick glacier (Meier and others, Reference Meier1994; yellow squares), and of 1–2 m sediment cores collected in 2011 (gray circles).

Fig. 3. (a) Seismic profile along the length of the outer basin, directly north of the moraine (A-A’). The glacier terminus is currently (in 2016) ~12 km upstream (to the left) of this profile, and the crest of the 1980 moraine is ~1 km to the right. White vertical dashes mark the terminus position in the year indicated. The heavy black vertical line represents the position and depth of the outer borehole drilled through ~1 km of ice in 1987. Colored curves indicate the interpreted former bed of the glacier at the base of the post-retreat sediment package in the fjord (green), the sediment/water interface in 2011 (magenta) and the interpreted seabed depth in 1997 (blue) based on bathymetric measurements. (b) Sonar water-depth profile across the inner basin (Fig. 2 for all locations).
The seismic-reflection profiles were single-channel data, which do not provide information about seismic velocities that can be used to determine sediment thickness. Thus, the data were migrated and depth-converted using a generic seismic speed of 1500 m s−1, which is representative of speeds in unconsolidated glacial marine sediments collected in the cores, as well as through brackish (~30 psu), cold (~6°C) water, as measured in Columbia Fjord (personal communication from S Gay, 2011; Fu-Xing and others, Reference Fu-Xing, Jian-Guo and Kun2012). Compaction of the sediments at depth will result in the total sediment thickness being slightly underestimated (Michalchuk and others, Reference Michalchuk2009; Milliken and others, Reference Milliken, Anderson, Wellner, Bohaty and Manley2009), as we use this reference speed for the entire sediment thickness. Depth-converted seismic profiles were analyzed using the open-source seismic interpretation software, OpendTect 4.4.0 (dGB Earth Sciences).
The seismic surveys and depth soundings revealed a large terminal moraine complex (morainal shoal) spanning the entrance to the fjord, where the water depth reaches a minimum of ~5–10 m (Fig. 2). It marks the advanced, stable position of Columbia Glacier up to 1980. The fjord contains two distinct sediment basins, one extending from this ‘1980 moraine’ to a sill midway down the fjord, and the second from the sill to the modern terminus; they are referred to herein as the ‘outer basin’ and ‘inner basin,’ respectively (Fig. 2).
3.2. Sediment volume calculations
For each seismic profile, the reflections corresponding to the top and bottom of the post-retreat sediment package were defined (Fig. 3a). The depth of the seabed reflector was compared with the independently measured sonar bathymetry to ensure consistency (Fig. 3b). The bottom of the sediment package was chosen as the most continuous and distinct reflection where the seismic facies changed from relatively high amplitude, parallel and continuous above to a low-amplitude and discontinuous facies below. The choice of the bottom reflection and the accuracy of our depth conversion are supported by the close agreement (<5%) between the altitude of the former glacier bed from a glacier borehole measurement (Meier and others, Reference Meier1994) and the seismically chosen depth of the base of the sediments at the same location (Fig. 3a). In addition, a continuous reflector interpreted to be the 1997 seabed is shown in Figure 3a based on water-depth measurements in 1997 by A. Post and B. Hallet (published by Krimmel, Reference Krimmel2001). This surface was interpolated throughout the outer basin and used to calculate the total volume of sediment deposited between the moraine and the sill from the start of retreat in 1980 until 1997, when the glacier had retreated well north of this basin.
To calculate the total sediment volume in the fjord, the surfaces of the seabed and the base of the post-retreat sediment package were interpolated across the area of the basins containing sediments from the crest of the 1980 moraine to the 2011 terminus, using both the inverse distance weighting and triangulation methods. The difference between the top and bottom surfaces provides the volume of sediment that accumulated in 31 a for each interpolation method, 0.33 km3 from inverse distance and 0.30 km3 from triangulation. The sediment volume was also estimated as 0.31 km3 simply based on the approximate mean basin width, sediment thicknesses and sidewall slopes. The consistency of these estimates provides confidence in the estimated total sediment volume and helps assess the uncertainty. This volume underestimates the total sediment output of Columbia Glacier because: (1) it focuses on the fine-grained, well laminated sediments in the basin and does not fully account for coarser deposits that are difficult to differentiate seismically from the underlying, consolidated sediment or bedrock; (2) it does not include the volume of sediment deposited beyond the moraine into Prince William Sound, which is expected to be significant early in the retreat phase, when the terminus was close to the moraine crest and the outer basin had not formed.
From the total volume of fine-grained sediment in the recently deglaciated Columbia Fjord, calculated as an average of the above methods to be at least 0.32 ± 0.10 km3, corresponding sediment fluxes for the two time periods constrained by water-depth measurements, 1980–1997 and 1998–2011, averaged at least 3.0 ± 0.9 × 106 m3 a−1 and 19 ± 6 × 106 m3 a−1, respectively.
3.3. Uncertainty estimates
Uncertainties in the sediment volume and flux arise from several sources. The volume of sediment calculated by the three methods of interpolating the seismic horizons that represent the top and bottom of the sediment package varies by ~15%. In addition, the chosen seismic velocity of 1500 m s−1 is likely too slow for the more consolidated sediments at the base of the deposits. The difference between a sonic velocity of 1500 m s−1, used here as the most appropriate velocity for water and the shallow, unconsolidated sediments and 1550 m s−1, the velocity found to be consistent with the seismic properties of ~100 m long cores of glacimarine sediments from the Antarctic Peninsula (Michalchuk and others, Reference Michalchuk2009; Milliken and others, Reference Milliken, Anderson, Wellner, Bohaty and Manley2009), is ~3%. Hence, by using the lower speed over the entire deposit, we likely underestimate the sediment thickness, and thus the volume, by at most ~3%. This seismic-speed-related error is most likely less, however, because the fjord narrows downward, so the deeper parts of the sediment package account for a smaller fraction of the total volume. We note that the close agreement between the depths of the base of the sediments estimated from the seismic profiles here and the base of the sediments encountered in the glacier drill core suggest that our use of 1500 m s−1 is a close approximation for the entire package.
Our seismic surveys did not cover the regions within ~1.5 km of the west branch of Columbia Glacier because of icebergs blocking ship passage (Fig. 2). Based on a measured annual retreat for the entire glacier in 2011 of ~1.3 km (Fig. 1c), the area not surveyed received sediment for ~1.15 a from the west branch of the glacier. If we assume equal sediment output from each branch of Columbia Glacier, a total annual sediment flux of 19 × 106 m3 (average from 1998 to 2011), and account only for the portion deposited within ~1 km of the ice, we estimate the missing volume to be ~7 × 106 m3, or ~2% of the total volume in Columbia Fjord.
Additional uncertainty in our sediment volume and fluxes arises from our assumption that the fjord is a perfect sediment sink (further discussion in Section 5.2), i.e. that all of the sediment delivered by the glacier is captured within the inner and outer basins, and that Columbia Glacier is by far the dominant source of sediments. An estimated ~10% uncertainty is included to represent potential contributions from hillslopes and other secondary sources. This estimate is slightly lower than for similar studies (e.g. Koppes and Hallet, Reference Koppes and Hallet2006); however, the lack of evidence in the seismic and sonar profiles of material entering from the fjord sides (e.g. deltas or landslides; Fig. 3b) together with the lack of significant rivers entering the fjord and major hillslope failures, supports our lower value. Also, we do not see evidence in the seismic profiles for talus-slope deposits that would indicate substantial coarse-grained sediment deposition at the base of the steep slopes along the sides of the fjord. We emphasize the counteracting effect of these assumptions: whereas the glacier-supplied volume would be underestimated if sediment escaped from the fjord, it would be overestimated if sediment entered from sources other than the glacier.
Thus, summing all of the uncertainties, we assign a ±30% uncertainty to the sediment volume and flux calculations, and stress that our results likely underestimate the total sediment delivered by Columbia Glacier during its retreat.
3.4. Effective erosion rate
We also determined the basin-averaged bedrock erosion rate required to sustain the estimated flux of sediment, Q
sed, to the fjord throughout the retreat. This effective erosion rate,
![]() $\dot E$
, is averaged over the retreat period and the entire glacierized area, A:
$\dot E$
, is averaged over the retreat period and the entire glacierized area, A:
For the 1000 km2 catchment, we use an average bedrock density, ρ
rock, of 2700 kg m−3, a reasonable mean value for the deformed metasedimentary and sedimentary rocks that dominate the Columbia Glacier Basin bedrock (Winkler, Reference Winkler1992). From our 1–2 m long sediment cores, we measured a dry bulk density, ρ
sed, of 1000 ± 100 kg m−3. Because this latter density reflects only the unconsolidated near-surface sediments, for the erosion calculation we use an average dry bulk density of 1300 kg m−3, representative of glacimarine sediment collected in many settings to depths of tens of meters (e.g. Milliken and others, Reference Milliken, Anderson, Wellner, Bohaty and Manley2009). The minimum effective erosion rate averages ~5.1 ± 1.5 mm a−1 during the 30 a retreat; it increases from ~2 mm a−1 during initial stage of retreat (until 1997) to ~15 mm a−1 during the 2000s. The relationship between
![]() $\dot E$
and the actual erosion rate is addressed below (Section 5).
$\dot E$
and the actual erosion rate is addressed below (Section 5).
4. GLACIMARINE SEDIMENTATION MODEL
4.1. Model development
To further explore the evolution of the sediment deposits in the fjord and the relationships between sediment delivery, sediment accumulation and redistribution, and glacier retreat, we developed a numerical model of fjord sedimentation over the 30 a retreat. Building on the average sediment fluxes we obtain directly from the seismic profiles for the two periods of retreat, discussed in Section 3.2, we model a more detailed sediment-flux history by using the known rate of retreat, the sediment thickness and stratigraphic architecture in the fjord, as well as published patterns of sedimentation near other temperate tidewater glaciers.
Inferring the sediment-flux history from the characteristics of the resulting sediment accumulation and the retreat history, is an inherently difficult inverse problem however, because little is known about the redistribution of sediments after their initial deposition, and the redistribution is most likely unpredictable due to diverse processes affecting the fjord bottom (e.g. submarine slides, gouging by large icebergs, calving-induced tsunamis). Moreover, short periods of high sediment flux can be offset by equivalent periods of low flux; hence the sediment-flux history derived from the model is fundamentally nonunique. Our approach is on the forward problem, to define how sustained changes in sediment flux affect the resulting accumulation of sediment in front of the retreating glacier terminus. Although we do not use a formal inversion technique, we can instructively constrain the low-frequency sediment-flux history, corresponding roughly to periods of years, from Columbia Glacier by exploring the sediment-flux history and parameter space in the model (the forward problem) that yields sediment accumulations closely matching our extensive observations.
Our model is guided by field studies of sedimentation in fjords (e.g. Cowan and Powell, Reference Cowan, Powell, Anderson and Ashley1991), and it builds on the 1-D model of Koppes and Hallet (Reference Koppes and Hallet2002), in which the sediment accumulation rate,
![]() $\dot S(x,\;t)$
, decreases exponentially with distance down fjord from the terminus, x:
$\dot S(x,\;t)$
, decreases exponentially with distance down fjord from the terminus, x:
where
![]() ${\dot S_{\rm o}}(t)$
is the time varying accumulation rate at the ice front, and δ represents the fall-off distance of the accumulation rate, or the distance over which the rate drops 1/e of the value at the terminus. The sediment thickness at any location, S (x), is the time integral of the sediment accumulation rate. Koppes and Hallet (Reference Koppes and Hallet2002) showed that, if rates of retreat and sediment accumulation at the ice front are both constant over long periods, the integral simplifies to:
${\dot S_{\rm o}}(t)$
is the time varying accumulation rate at the ice front, and δ represents the fall-off distance of the accumulation rate, or the distance over which the rate drops 1/e of the value at the terminus. The sediment thickness at any location, S (x), is the time integral of the sediment accumulation rate. Koppes and Hallet (Reference Koppes and Hallet2002) showed that, if rates of retreat and sediment accumulation at the ice front are both constant over long periods, the integral simplifies to:
The resulting sediment thickness scales with the accumulation rate at the ice front and inversely with the retreat rate,
![]() $\dot R$
. Equation (3) expresses quantitatively the intuitive result that, if the sediment output from the glacier were constant in time, a faster retreat would distribute the same volume of sediment over a greater area, forming a thinner deposit. We note that under these conditions, the steady-state sediment flux, Q
ss, necessary to sustain the rate of accumulation at the ice front is
$\dot R$
. Equation (3) expresses quantitatively the intuitive result that, if the sediment output from the glacier were constant in time, a faster retreat would distribute the same volume of sediment over a greater area, forming a thinner deposit. We note that under these conditions, the steady-state sediment flux, Q
ss, necessary to sustain the rate of accumulation at the ice front is
![]() ${\dot S_{\rm o}}\delta W$
, where W is the width of the fjord where the sediments are accumulating. In reality, both
${\dot S_{\rm o}}\delta W$
, where W is the width of the fjord where the sediments are accumulating. In reality, both
![]() ${\dot S_{\rm o}}(t)$
and
${\dot S_{\rm o}}(t)$
and
![]() $\dot R(t)\; $
vary in time. Hence, the sediment thickness in any location reflects the complex history of both rates of retreat and sediment accumulation. If the retreat rate is known, as in the case of Columbia Glacier, the time variation of the sediment accumulation, represented by
$\dot R(t)\; $
vary in time. Hence, the sediment thickness in any location reflects the complex history of both rates of retreat and sediment accumulation. If the retreat rate is known, as in the case of Columbia Glacier, the time variation of the sediment accumulation, represented by
![]() ${\dot S_{\rm o}}(t)$
, can be calculated from the observed sediment thickness, S.
${\dot S_{\rm o}}(t)$
, can be calculated from the observed sediment thickness, S.
In view of observations of fast sediment accumulation near the glacier terminus with slower but significant accumulation extending many kilometers down fjord, we model the total sediment delivery as the sum of ice-proximal and ice-distal sedimentation, represented by two exponential distributions with short and long fall-off distances, δ 1 and δ 2, respectively:
The history of the sediment flux from the glacier, Q (t), must account for sediment accumulation over the entire fjord bottom, from the ice front to the far field, and across the fjord:
where
![]() $\hat W$
is the representative width of the fjord bottom near the terminus, where much of the sediment accumulates, as discussed in Section 4.2. Substituting Eqn (4) in (5) yields the glacier sediment flux that we calculate with the model:
$\hat W$
is the representative width of the fjord bottom near the terminus, where much of the sediment accumulates, as discussed in Section 4.2. Substituting Eqn (4) in (5) yields the glacier sediment flux that we calculate with the model:
In the model, we represent explicitly both primary proglacial sedimentation (Eqn (4)) and secondary reworking, such that the change in seabed elevation reflects sediment derived directly from the glacier as well as subsequent accumulation or erosion due to differential downslope transport in the form of slumping, iceberg gouging and other diffusional processes. We begin with the simple conservation of mass in 1-D, along the length of the fjord, where the change in seabed elevation is the divergence in the flux of sediment, q, per unit cross-sectional area:
We assume that the rate of downslope sediment transport is proportional to the seabed gradient:
where κ is an effective diffusivity of the sediments. Combining Eqns (7) and (8), and incorporating the sediment delivery terms (Eqn (4)), yields the rate of change of the seabed elevation due to both direct sediment delivery from the glacier and diffusive downslope transport:
In essence, we model the gravitational redistribution of sediment throughout the fjord basin as a diffusive process, where the diffusivity, κ, represents broadly a ‘mobility factor’ for fjord sediment. This simple approach enables us to model the distribution of sediment and the stratigraphic architecture of sediment packages in any fjord, as functions of retreat and sediment-flux histories, fjord geometry and sediment mobility. For a system like Columbia Glacier, for which the basin geometry, sediment distribution and ice retreat history are all relatively well known, the model can be used to infer, in considerable detail, the time-varying delivery of sediment to the fjord by the glacier.
4.2. Application to Columbia Glacier
Using Eqns (6) and (9), we model the evolution of the sediment accumulation in Columbia Fjord over a ~20 km long transect along the fjord extending from the 1980 to the 2011 terminus positions. The retreat rate and fjord widths are determined directly from our observational dataset. The temporal history of sediment delivery is the principal objective of the modeling; the decay distances and sediment diffusivity are poorly known model parameters that are addressed in Section 4.3.
The retreat rate is calculated from the terminus positions mapped from aerial photographs for 1980–2000 (Krimmel, Reference Krimmel2001) and by time-lapse photography for 2000–2010 (Written communication from T. Pfeffer, 2013) (Figs 1b, c). We model the retreat rate by adjusting the position of the terminus, x = 0, at each time step.
As the fjord is valley shaped, the width of the accumulation zone at any reach of the fjord increases with time as the sediment deposit thickens. We account for the widening by assuming a parabolic shape corresponding to fjord cross sections that are observed in both the seismic and sonar data and are generally representative of glacier valleys (Fig. 3b; e.g. Harbor, Reference Harbor1992). The rate at which the width increases as the basin fills is constrained by a scaling factor, a (x), for each along-fjord location dependent on the measured sediment thickness, S (x, t 2011) and seafloor width, W (x, t 2011):
 $$S(x,\;{t_{2011}}) = \alpha (x){\left( {\displaystyle{{W(x,\;{t_{2011}})} \over 2}} \right)^2},$$
$$S(x,\;{t_{2011}}) = \alpha (x){\left( {\displaystyle{{W(x,\;{t_{2011}})} \over 2}} \right)^2},$$
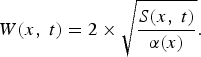 $$W(x,\;t) = 2 \times \sqrt {\displaystyle{{S(x,\;t)} \over {\alpha (x)}}}. $$
$$W(x,\;t) = 2 \times \sqrt {\displaystyle{{S(x,\;t)} \over {\alpha (x)}}}. $$
In addition, we account for down-fjord width variations. Due to the exponentially greater accumulation of sediment near the terminus for both ice-proximal and ice-distal sedimentation (Eqn (4)), we weight the widths,
![]() ${\hat W_1}$
and
${\hat W_1}$
and
![]() ${\hat W_2}$
, in Eqn (6) with the corresponding sediment accumulation from the ice front to twice the distances δ
1 and δ
2 to represent ~90% of the total sediment delivered. This down-fjord weighting accounts for scenarios where, for example, the fjord narrows away from the ice, and as most of the sediment is deposited near the wider terminus, the ice-proximal width must be more heavily weighted. Thus, the modeled sediment flux accounts for the significant down-fjord variations in both width and sediment-accumulation rate.
${\hat W_2}$
, in Eqn (6) with the corresponding sediment accumulation from the ice front to twice the distances δ
1 and δ
2 to represent ~90% of the total sediment delivered. This down-fjord weighting accounts for scenarios where, for example, the fjord narrows away from the ice, and as most of the sediment is deposited near the wider terminus, the ice-proximal width must be more heavily weighted. Thus, the modeled sediment flux accounts for the significant down-fjord variations in both width and sediment-accumulation rate.
The average sediment fluxes we calculated for the two well defined time intervals (1980–1997 and 1998–2011) provide the first-order sediment-flux history and the base on which we optimize the model. We determine our initial values for
![]() ${\dot S_{{\rm o1}}}$
and
${\dot S_{{\rm o1}}}$
and
![]() $\; {\dot S_{{\rm o2}}}$
for the two time periods using the average sediment thickness and retreat rate, as well as the reference, steady-state sediment flux,
$\; {\dot S_{{\rm o2}}}$
for the two time periods using the average sediment thickness and retreat rate, as well as the reference, steady-state sediment flux,
![]() ${Q_{{\rm ss}}} = {\dot S_{\rm o}}\delta W$
, subdivided equally into proximal and distal contributions. We have no direct constraint on the relative contribution from proximal and distal processes at Columbia Glacier, but field data suggest bedload and suspended load are comparable for temperate glaciers (e.g. Hallet and others, Reference Hallet, Hunter and Bogen1996); so for model simplicity we approximate that the volumes of sediment delivered by proximal and distal accumulation in a fjord of relatively uniform width are the same and set
${Q_{{\rm ss}}} = {\dot S_{\rm o}}\delta W$
, subdivided equally into proximal and distal contributions. We have no direct constraint on the relative contribution from proximal and distal processes at Columbia Glacier, but field data suggest bedload and suspended load are comparable for temperate glaciers (e.g. Hallet and others, Reference Hallet, Hunter and Bogen1996); so for model simplicity we approximate that the volumes of sediment delivered by proximal and distal accumulation in a fjord of relatively uniform width are the same and set
![]() ${\dot S_{{\rm o1}}}{\delta _1} = {\dot S_{{\rm o2}}}{\delta _2}$
. Sedimentation fall-off distances most consistent with published in situ sediment-trap measurements (Cowan and Powell, Reference Cowan, Powell, Anderson and Ashley1991) are of the order of 102 and 104 m for δ
1 and δ
2, hence we use these values.
${\dot S_{{\rm o1}}}{\delta _1} = {\dot S_{{\rm o2}}}{\delta _2}$
. Sedimentation fall-off distances most consistent with published in situ sediment-trap measurements (Cowan and Powell, Reference Cowan, Powell, Anderson and Ashley1991) are of the order of 102 and 104 m for δ
1 and δ
2, hence we use these values.
We refine the sediment-flux history by dividing the 30 a retreat into 10 discrete time intervals during which retreat rates were relatively constant (bracketed by 1980, 1986, 1991, 1997, 1998, 2000, 2003, 2006, 2007, 2008, 2011). For each interval, we effectively adjust the model parameters in Eqns (6) and (9); we multiply the initial mean values of
![]() ${\dot S_{{\rm o1}}}$
and
${\dot S_{{\rm o1}}}$
and
![]() $\; {\dot S_{{\rm o2}}}$
calculated above by a scaling factor, such that the modeled 30 a of accumulation, modified by secondary reworking, approximates the observed sediment thickness distribution. First, the set of 10 scaling factors were chosen coarsely, by adjusting the initial
$\; {\dot S_{{\rm o2}}}$
calculated above by a scaling factor, such that the modeled 30 a of accumulation, modified by secondary reworking, approximates the observed sediment thickness distribution. First, the set of 10 scaling factors were chosen coarsely, by adjusting the initial
![]() ${\dot S_{\rm o}}$
value by 50 or 150%. We then adjusted the set of factors sequentially, at finer intervals of 10%, until the resulting sediment-flux history produced sediment deposits generally consistent with the observed sediment thickness distributions in 1997 and 2011. The same scaling factors were applied to both proximal and distal accumulation terms.
${\dot S_{\rm o}}$
value by 50 or 150%. We then adjusted the set of factors sequentially, at finer intervals of 10%, until the resulting sediment-flux history produced sediment deposits generally consistent with the observed sediment thickness distributions in 1997 and 2011. The same scaling factors were applied to both proximal and distal accumulation terms.
4.3. Model results
The optimal model output was chosen as the sediment-flux history that produces: (1) a sediment distribution pattern minimizing the RMS difference between the modeled bathymetry and the actual bathymetry measured in both 1997 and 2011 and (2) a sediment accumulation with internal architecture generally consistent with that of the sediments imaged in the seismic profiles (Figs 4a, b). This resulting sediment-flux history is consistent with the measured sediment volume deposited between 1980 and 1997, the total volume deposited from 1980 to 2011 (Fig. 5a), as well as the fivefold sediment flux increase from ~4 × 106 m3 a−1 to ~20 × 106 m3 a−1 that started ~1997. While the many variables involved in the modeled solution inherently produce a non-unique sediment-flux history, the extensive observational constraints severely limit the plausible model parameter space and the corresponding modeled history.

Fig. 4. Model output of the sediment deposits created during the retreat of Columbia Glacier, which proceed from right to left; stars mark annual terminus positions from 1980 to 2010, with specific years shown. Both (a) and (b) show the measured base of the postglacial sediment package (heavy black curve), material underlying the sediments (gray shaded area) and measured fjord depth (blue curve). The ‘outer basin’ extends between the moraine (18 km) and sill (8 km), and the ‘inner basin’ extends from the modern glacier terminus (0 km) to the sill. In (a), fine curves represent the interpreted seabed in 1997 (black, shown in Fig. 3), modeled seabed in 1997 (magenta) and 2011 (red). In (b), modeled seabed as a function of time is shown by thin colored curves. Thick red line is the final modeled seabed in 2011, as in (a). Thin lines above the thick red line (e.g. ~8 km) are areas where some of the sediment was removed and redistributed. Vertical lines form where the glacier terminus was located at annual increments during the retreat.

Fig. 5. (a) Sediment-flux history. Blue and green dashed lines show the average flux for 1980–1997 and 1998–2010, estimated from the calculated seismic volumes without using the model. The thick black curve shows the total modeled sediment flux through time; the blue and red curves indicate components attributed to proximal and distal accumulation (Eqn (6)), respectively. (b) Sediment thickness distribution as a function of distance from the 2011 terminus; measured from seismic profiles (black), and modeled (red). Deposits on the sill (~8 km), and on the moraine (16–18 km) are not represented by the model (see Section 4.3 for explanation).
By exploring the model parameter space, we highlight aspects of the modeled history that are robust using diverse inputs, as well as those features that are less well constrained or sensitive to the choice of model parameters. Our range of sedimentation fall-off distances for δ 1 and δ 2 is constrained by field observations (Cowan and Powell, Reference Cowan, Powell, Anderson and Ashley1991), thus we vary these values on the order of 102 and 104 m, respectively. Figure 6 illustrates how the diffusivity and long fall-off distance affect the shape of the sediment deposits and internal stratigraphic architecture; they depend most strongly on the sediment diffusivity, κ. In Figure 7, the brown curve shows the flux history without any scaling factors, which overestimates the volume of sediment in the basin and does not produce the observed internal architecture. To assess the robustness of the sediment-flux peak ~2001 we can, for example, double the scaling factors in the following time period and halve them around the peak (purple curve in Fig. 7). We also change the decay distances, and find that with many perturbations of the model input, the timing of the peak flux is robust. The higher-frequency changes in the flux ~2007/08 (Fig. 5a), however, are not consistent using various model parameters (Fig. 7), and are likely sensitive to the choice of scaling factors. Based on all of the model runs analyzed to produce the optimized flux history, our final sediment-flux history uses a diffusivity of 106 m2 a−1 and a set of scaling factors of 0.5, 1.0, 1.7, 1.6, 0.5, 0.6, 0.6, 0.8, 3.1, 1.0 for intervals bracketed by 1980, 1986, 1991, 1997, 1998, 2000, 2003, 2006, 2007, 2008, 2011. We feel most confident in the low flux prior to 1997, the peak in flux ~2000/01, and the flux increase for the 2008–2011 period (Fig. 5a).

Fig. 6. Relationship between the RMS error (measured as the distance between the modeled and the actual bathymetry) and the diffusivity constant, κ. Colors indicate the value of the long decay distance, δ 2; here, δ 1 is held at 100 m. A diffusivity of 106 m2 a−1 was chosen to generate the model results presented herein, as it minimizes the RMS difference between the model and the actual fjord bathymetry.

Fig. 7. Range of sediment flux histories consistent with sediment accumulation in the Columbia Fjord up-glacier from the moraine illustrating the model sensitivity to different parameters. The exponential decay distances (m), δ 1 and δ 2 (six thin curves defined in the legend) influence slightly the sediment flux histories. Horizontal dashed green lines represent the average flux determined independently of the model for the two constrained time periods. The thick lines show effects of the scaling on the modeled flux history: without scaling, it overestimates the total sediment volume (brown), and modifying the optimal scaling (black) by doubling the flux during the time period indicated in the legend, and halving it during the preceding interval (blue and purple). In both instances, the total sediment volume is overestimated and the architecture of the basin is not optimized. Thick red curve shows the flux history when sediment escaping over the moraine is taken into account. For all histories shown here, κ is held constant at 106 m2 a−1.
While the modeled sediment-flux history reproduces the sediment thickness distribution and internal stratigraphy of the outer and inner basins, it does not account for sediments on the major sill, or the perched deposits on the 1980 moraine (Fig. 5b). The sediments on the sill are not well imaged in the seismic profiles, however, and we lack sediment samples from the area. As both the sill and perched deposits are situated in high points along the basin, and the other sediment deposits fill basins with minimal surface slope, these ‘perched’ deposits may be composed of coarser-grained sediment that would be considerably less mobile than the finer sediments filling most of the basin. We could account for these less mobile deposits by introducing variable sediment diffusivity, but such a change would require an additional model parameter that is not well constrained and is not justified because these sediments account for ~5% of the total sediment volume. On the other hand, using a lower diffusivity for the entire fjord would not optimize the modeled sediment packages in the basins that are well imaged (Fig. 6). Thus, we retained a single, sediment diffusivity value for all of the sediment deposits, but stress that the model does not address the ~5% of the sediments in the ‘perched’ deposits nor the construction of morainal shoals and other deposits likely comprising much less mobile sediment.
5. DISCUSSION
5.1. Implications for the formation and evolution of fjord sediment deposits
New bathymetric and seismic data, when interpreted in the context of mid-retreat (1997 and 2004) bathymetry measurements (Krimmel, Reference Krimmel2001; Noll, Reference Noll2005) and the 1987 boreholes through nearly 1000 m of glacier ice (Meier and others, Reference Meier1994), closely constrain the depositional evolution of the sediments that accumulated during the 30 a retreat of Columbia Glacier. While distinct packages of stratified, flat-lying sediments in fjord basins are often interpreted as having formed proglacially after glacial retreat, rather than being remnants from a previous glacial cycle (e.g. Powell, Reference Powell, Anderson and Ashley1991; Hallet and others, Reference Hallet, Hunter and Bogen1996; Koppes and Hallet, Reference Koppes and Hallet2002, Reference Koppes and Hallet2006), studies of other Alaskan glaciers and fjords show that substantial packages of unlithified sediments can be overridden by ice (e.g. Motyka and others, Reference Motyka, Truffer, Kuriger and Bucki2006; Cowan and others, Reference Cowan2010). After drilling the boreholes through Columbia Glacier, only ~7 cm of sand and gravel was found under the glacier at the outer borehole site; the inner-basin borehole was underlain by ~60 cm of fine-grained sediment (Humphrey and others, Reference Humphrey, Kamb and Fahnestock1993). That only decimeters of subglacial sediments were found above the consolidated base of the glacier supports our interpretation that the tens of meters of sediments measured in the basins were deposited since the most recent glacier retreat. This provides us confidence in our interpretation of the former glacier bed in the seismic profiles and in defining the sedimentary evolution of Columbia Fjord (Fig. 3a).
During Columbia Glacier's 30 a rapid retreat, the sediment flux from the glacier averaged at least 1.1 ± 0.3 × 107 m3 a−1, which is the same order of magnitude as the sediment fluxes estimated from other major temperate Alaskan glaciers (e.g. Hallet and others, Reference Hallet, Hunter and Bogen1996; Hunter and others, Reference Hunter, Powell and Lawson1996; Seramur and others, Reference Seramur, Powell and Carlson1997; Cowan and others, Reference Cowan2010). At the broadest temporal scale, the constraints on the sediment flux provided by the terminus positions and the bathymetric measurements suggest that the glacier delivered approximately five times more sediment to the fjord during the 1998–2011 period than in the 1980–1997 period. As further discussed in Section 5.3, we attribute this dramatic increase in flux to an increase in the sediment-transport capacity of the subglacial hydraulic system. The filling of about three quarters of the outer basin long after the glacier had retreated across this area, challenges the common assumption that sediment derived from a glacier only fills the most proximal basin (e.g. Cowan and Powell, Reference Cowan, Powell, Anderson and Ashley1991; Cowan and others, Reference Cowan2010), and suggests that sediment is transported efficiently throughout the fjord, including passing over significant sills (exceeding tens of meters in height).
To determine whether the calculated sediment fluxes are physically reasonable in view of the common inference that sediments in temperate glaciers are largely transported in the subglacial hydraulic network (e.g. Hunter and others, Reference Hunter, Powell and Lawson1996), and to consider the cause of the sediment-flux increase, we compare the overall water and sediment budgets of Columbia Glacier. The principal sources of water in the subglacial hydraulic system are surface melting (ablation) and rainfall. Using Table 2 from Rasmussen and others (Reference Rasmussen, Conway, Krimmel and Hock2011), modeled rates of surface ablation are 3.1 and 3.6 km3 w.e. a−1 for 1982–1995 and 1996–2007, respectively. We assume that rainfall is simply the difference between surface accumulation and modeled total precipitation, estimated to average 5.5 km3 w.e. a−1 over the ~103 km2 basin from 1982 to 2007. For the two periods, 1982–1995 and 1996–2007, the estimated precipitation totals 5.8 and 5.2 km3 w.e. a−1, respectively. These estimates are consistent with precipitation records from nearby Valdez, which indicate the first period was ~10% wetter than the second (Personal communication from A. Rasmussen, 2015), while the surface accumulation totals were 4.2 and 3.1 km3 w.e. a−1. Accordingly, we estimate the total subglacial water discharge to be 4.7 and 5.7 km3 w.e. a−1, for 1982–1995 and 1996–2007, respectively. The mean annual sediment fluxes for these periods (~3 × 106 m3 a−1 to ~20 × 106 m3 a−1) suggest that the overall sediment concentration of the subglacial meltwater, including both suspended load and bedload, averaged ~1 g L−1 for early retreat and ~5 g L−1 from the later period. If we assume roughly half the total sediment load is carried in suspension, the suspended sediment concentrations would average ~0.4 and ~2.3 g L−1 for the two retreat periods, well within the range of suspended concentrations measured in streams emanating from glaciers terminating on land (Pearce and others, Reference Pearce2003; Riihimaki and others, Reference Riihimaki, Macgregor, Anderson, Anderson and Loso2005; Swift and others, Reference Swift, Nienow and Hoey2005), and suggesting that the water flux is sufficient to carry the sediment load subglacially (e.g. Hunter and others, Reference Hunter, Powell and Lawson1996). This comparison further suggests that during the times of high subglacial water discharge, such as, occurs seasonally and after large storms, the suspended-sediment concentrations will be substantially greater.
Previous modeling approaches, while successful in calculating glacial sediment fluxes, have not addressed the internal stratigraphy and basin geometry of fjord sediments (e.g. Koppes and Hallet, Reference Koppes and Hallet2002; Mugford and Dowdeswell, Reference Mugford and Dowdeswell2011). The processes represented by diffusion and the two exponential sedimentation terms (Eqn (9)) play key roles in the transport and distribution of sediment throughout the fjord, particularly in the delivery of sediment to the outer basin after 1997 and formation of the horizontal seabed. Modeling the sediment delivery from the glacier using a single exponential term can only account for sediment deposition either close to or far from the ice. Two terms are essential to represent both proximal (modeled using a short fall-off distance, δ 1) and distal sediment transport and deposition. The latter term suggests that efficient transport mechanisms deliver significant volumes of glacial sediment many kilometers from the terminus. In addition to mechanisms representing sediment deposition, the model simulates broadly the gravitational redistribution of fjord sediments, a critical process in forming the observed steep-sided walls free of sediment and nearly horizontal internal stratigraphy common in temperate fjords (Carlson, Reference Carlson1989; Cai and others, Reference Cai, Powell, Cowan and Carlson1997; Koppes and Hallet, Reference Koppes and Hallet2002, Reference Koppes and Hallet2006; Cowan and others, Reference Cowan2010). These features cannot be taken into account without considerable diffusive redistribution, represented by high diffusivities (κ values) (Fig. 6).
The dominant sediment-transport process within the fjord depends strongly on the concentration of sediment suspended in the subglacial meltwater entering the fjord. For concentrations in excess of ~30 g L−1, the density of the sediment-laden meltwater exceeds the density of the ambient fjord seawater measured in Columbia Fjord (Mulder and Syvitski, Reference Mulder and Syvitski1995; personal communication from S. Gay, 2011), and the resulting high-concentration gravity flows are capable of carrying sediment along the fjord seabed far from the source (e.g. Prior and others, Reference Prior, Bornhold, Wiseman and Lowe1987; Syvitski and others, Reference Syvitski, Burrell and Skei1987; Willems and others, Reference Willems, Powell, Cowan and Jaeger2011). These flows, along with redistribution processes such as slumping on diverse scales, iceberg gouging, iceberg melting, waves generated from calving icebergs and deep currents driven by tides and toppling of massive icebergs, are presumably responsible for the high mobility of the sediment, the flat seabed and the approximately horizontal, parallel internal layering (e.g. Syvitski, Reference Syvitski1989). The few existing in situ measurements from river-fed fjords suggest turbidity currents occur regularly (e.g. Prior and others, Reference Prior, Bornhold, Wiseman and Lowe1987; Bornhold and others, Reference Bornhold, Ren and Prior1994).
For lower sediment concentrations, subglacial meltwater is buoyant, forms plumes and travels along the surface (e.g. Powell and Molnia, Reference Powell and Molnia1989; Syvitski, Reference Syvitski1989; Cowan and Powell, Reference Cowan, Powell, Anderson and Ashley1991; Hunter and others, Reference Hunter, Powell and Lawson1996), while sediment progressively flocculates and settles to the seabed (e.g. Hill and others, Reference Hill, Syvitski, Cowan and Powell1998; Curran and others, Reference Curran2004). Such pelagic sediment processes would tend to form drapes of sediment conforming to the underlying seafloor topography rather than filling in the lower portions of the basin to create a flat seabed. The sharp contrast between the level sediment surface and the surrounding valley slopes illustrates the importance of gravitational reworking relative to sediment settling through the water column (Fig. 3b).
5.2. Implications of fjords as perfect sediment traps
We examine our assumption of the fjord as a perfect sediment trap by estimating the volume of sediment that was likely transported over the 1980 moraine during the retreat period. The sediment flux transported beyond the moraine is estimated simply by integrating the sediment accumulation rate,
![]() $\dot S(x,\;t)$
in Eqn (2) from the position of the moraine (rather than the position of the terminus, as used in Section 4.1) to infinity. The fraction of sediment that exited the fjord ranges from 1, when the glacier terminus is at the moraine (x = 0), to zero when the terminus is very far from the moraine (as x→ ∞). Based on the retreat history of Columbia Glacier, we estimate that the exit fraction from both proximal and distal accumulation during the 30 a retreat sums to ~5 × 107 m3, or ~15% of the total sediment volume in the fjord. The fraction of sediment exiting the fjord ceases to be highly significant (i.e. <40% of the total flux) when the glacier retreats more than 2 km from the moraine. Figure 7 illustrates the flux history accounting for the loss of sediment over the moraine.
$\dot S(x,\;t)$
in Eqn (2) from the position of the moraine (rather than the position of the terminus, as used in Section 4.1) to infinity. The fraction of sediment that exited the fjord ranges from 1, when the glacier terminus is at the moraine (x = 0), to zero when the terminus is very far from the moraine (as x→ ∞). Based on the retreat history of Columbia Glacier, we estimate that the exit fraction from both proximal and distal accumulation during the 30 a retreat sums to ~5 × 107 m3, or ~15% of the total sediment volume in the fjord. The fraction of sediment exiting the fjord ceases to be highly significant (i.e. <40% of the total flux) when the glacier retreats more than 2 km from the moraine. Figure 7 illustrates the flux history accounting for the loss of sediment over the moraine.
We further examine the extent to which the approach described above overestimates the escaped volume, because we did not account for the high moraine that would tend to block sediment exiting the fjord. Based on the optimized sediment-flux history (Fig. 8) and Eqn (2), disregarding the moraine, we estimate the sediment accumulation rate 10 km down fjord during the retreat period to average ~5 cm a−1. Previous studies in Prince William Sound show that the sediment-accumulation rate averaged over the past 100 a near the moraine of Columbia Glacier is ~2 mm a−1, and that the sediment is derived from multiple sources (Jaeger and others, Reference Jaeger and Nittrouer1999). Our estimate of a much higher accumulation rate than observed suggests that during the retreat, the high moraine did impede sediment exiting the fjord, which is consistent with the morphology of the seafloor. As mentioned previously, the distinct flat bottom suggests gravity-driven processes dominate sediment redistribution, and it is unlikely that large amounts of sediment ‘climb’ more than 200 m out of the fjord basin. Thus, the total potential loss of sediment from the fjord is well accounted for in our 30% uncertainty in the sediment yield, as we stress that our sediment-yield calculations are likely underestimates.

Fig. 8. Temporal variations of retreat rates (red), and interpolated ice flux (blue) from O'Neel and others (Reference O'Neel2013) and of modeled sediment flux (black). Ice flux estimates are derived from over 120 velocity fields measured over the 1977–2013 interval at four fixed-location cross sections (‘flux gates’) along the glacier trunk. Glacier geometry is established from bathymetry, the McNabb and others (Reference McNabb2012) bed model and surface elevation fields. The 265 resulting estimates of ice flux through the calving front are then smoothed at annual time steps using a nonparametric kernel-smoothing filter (Bowman and Azzalini, Reference Bowman and Azzalini1997). We use a 3 a window sampled on 15 June each year, when the seasonal variation is near its average value.
5.3. Implications for glacial erosion and the subglacial storage of sediment
Temporal variations in the modeled sediment-flux history suggest two end-member interpretations for the yield of subglacial sediments (Fig. 8). The first, the erosion end member, is simply that all sediment delivered to the fjord is newly eroded bedrock. The other, the sediment remobilization end member, is that the sediment delivered to the fjord is evacuated from over-deepened subglacial basins or more widely distributed deposits under the glacier. The potential sub-aerial contribution of sediments is ignored because ice covers much of the catchment.
For the erosion end member, the basin-averaged erosion rate over the 30 a retreat is 5.1 ± 1.5 mm a−1. The erosion rate varies with time and scales with the sediment flux; it ranges from ~2 to ~15 mm a−1. These rates are comparable with other nearby glaciated areas (Hallet and others, Reference Hallet, Hunter and Bogen1996), and the average is essentially identical to the regional Holocene average (Sheaf and others, Reference Sheaf, Serpa and Pavlis2003). However, the rates are lower than those reported by Koppes and Hallet (Reference Koppes and Hallet2002, Reference Koppes and Hallet2006), at least partly because we convert the fjord sediment to its rock equivalent using the dry bulk density measured in glacimarine sediments worldwide (~1300 kg m−3) and not the wet bulk density (~1700–2000 kg m−3), as used previously. The use of the wet bulk density resulted in a ~40% over estimate of erosion rates in these and related publications (e.g. Hallet and others, Reference Hallet, Hunter and Bogen1996). This correction has little significance, however, relative to the much larger correction made to account for the unusually dynamic state of the tidewater glaciers during retreat since the Little Ice Age (Koppes and Hallet, Reference Koppes and Hallet2002, Reference Koppes and Hallet2006).
The mean erosion rate of ~5 mm a−1 necessary to sustain the sediment flux during the entire period of retreat has interesting implications for inferring the behavior and stability of Columbia Glacier during periods of advance. In their model of tidewater glacier advance, Nick and others (Reference Nick, van der Veen and Oerlemans2007) found that in order for Columbia Glacier to advance into water deeper than 250–300 m under favorable climate conditions, sediment production sufficient to build a morainal shoal was required. They determined that a sediment-production rate equivalent to basin-wide erosion of ~4 mm a−1 was necessary for Columbia Glacier to advance at a realistic rate of ~30 m a−1, which is generally consistent with the most recent advance reconstructed from buried trees (Calkin and others, Reference Calkin, Wiles and Barclay2001). The close agreement between our calculated effective erosion rate for Columbia Glacier during its 30 a retreat and the estimated erosion rate necessary for the glacier to advance over many centuries supports our interpretation that the long-term erosion rate for this glacier is ~4–5 mm a−1.
Turning to the sediment remobilization end member, if the majority of sediment delivered to Columbia Fjord during the period of retreat were derived from subglacial basins, the outer basin, inner basin and the remaining subglacial basin(s) would all have been major potential sources of sediment during the retreat (Fig. 9). For the outer basin, the close match between the depth of the glacier borehole in the outer basin (386 m below sea level) and our interpreted sediment base (Fig. 3a), together with the thin (<1 m) subglacial sediment layer found at the base of the borehole, suggest that the outer basin did not supply significant stored sediment during the retreat (Humphrey and others, Reference Humphrey, Kamb and Fahnestock1993; Meier and others, Reference Meier1994). For the inner fjord basin, the up-glacier borehole was drilled through the ice reaching the bed at an elevation of ~−520 m, which is slightly deeper than our interpreted sediment base of −500 ± 10 m (Humphrey and others, Reference Humphrey, Kamb and Fahnestock1993; Meier and others, Reference Meier1994). If a ~10 m thick layer of sediment were evacuated from this entire inner basin, which covers an area of ~2.5 km2, the volume would be equivalent to ~2 a of the mean annual sediment load.

Fig. 9. Sequential longitudinal glacier profiles during the retreat (from O'Neel and others, Reference O'Neel2013). Glacier bed profiles from calculated glacier topography (solid black curve; McNabb and others, Reference McNabb2012) and from the base of the sediment package imaged in seismic profiles collected in this study (dashed black curve). Differences in the black curves reflect uncertainties in calculating the bed, sedimentation between ~55 and 67 km, and large transverse variations in basal depth near ~50 km. Note the steep reverse-sloping beds upvalley of ~48 and ~56 km.
Proceeding farther up the valley, for the existing subglacial basin ~46–48 km (Fig. 9) to supply the majority of the sediment flux, the average annual load would correspond to removing an ~2.5 m thick sediment layer annually over the basin area, which we estimate to be 4 km2 based on the McNabb and others (Reference McNabb2012) bed model and surface elevation fields. The potential contribution from the existing subglacial basin is difficult to quantify, as we have no estimates of the subglacial debris thickness. Recent observations from Taku Glacier, Alaska, however, highlight that soft sediment under the glacier can be evacuated so rapidly as to lower the ice/sediment interface at rates exceeding 4 m a−1 (Motyka and others, Reference Motyka, Truffer, Kuriger and Bucki2006). These observations, together with the known presence of a subglacial basin currently under Columbia Glacier, suggest that substantial volumes of sediment may well be stored and later evacuated from over-deepened subglacial basins.
We stress that while sediment can be stored subglacially, changes in the volume of stored sediment are short-lived transients when considering the centennial-to-millennial timescale of advances. The average sediment flux delivered by Columbia Glacier would result in the complete filling of the remaining subglacial basin in ~2 decades. Similar deep basins would quickly aggrade due to the influx of sediment from the subglacial hydraulic system. Because these basins would fill within decades, any sediment reaching the glacier terminus, and the long-term sediment flux, must be supplied by sediment produced by active bedrock erosion. Indeed, the remobilization end member further supports the erosion rate of 4–5 mm a−1 calculated here and by Nick and others (Reference Nick, van der Veen and Oerlemans2007) being effective over timescales of centuries or more throughout cycles of glacier advance and retreat.
5.4. Implications for the relationship between sediment flux and glacier dynamics
We now examine the model-derived sediment-flux history and assess the potential for the mobilization of substantial volumes of sediment stored subglacially using the extensive glaciological data for Columbia Glacier, including ice velocity, ice flux, glacier geometry, ice thickness and retreat history. A close relationship between the cross-section averaged ice velocity (ice flux per cross-sectional area, which in this case essentially equals sliding velocity), and the sediment flux for any glacier is generally expected due to the sliding speed control on the erosion rate by both quarrying and abrasion (Hallet, Reference Hallet1979; Iverson, Reference Iverson1991).
During the early period of retreat between 1980 and 1995, the retreat rate and ice flux both steadily increased, while the sediment flux remained at a relatively constant, low value until ~1997, coincident with the maximum ice flux (Fig. 8). From 1997 to 2000, the sediment flux increased fivefold as the retreating terminus had exposed the entire outer basin and the sill separating it from the adjacent upstream basin (Figs 3, 5a). As the terminus retreated from the sill into deeper water, the retreat accelerated (Fig. 8). A second abrupt increase in sediment flux between 2007 and 2011 coincides with increases in retreat rate and ice flux (Fig. 8). The sediment flux remained low prior to 1997, despite large increases in ice flux, demonstrating that the sediment flux is not simply related to sliding speed.
We hypothesize that the distinct increase in sediment flux reflects an increase in sediment transport in the subglacial hydraulic system, resulting in faster evacuation of water and sediment from under Columbia Glacier. To test this hypothesis, we assess the time-varying sediment flux from Columbia Glacier in light of the sediment transport capacity of the subglacial hydraulic system. This hydraulic system is controlled by the longitudinal geometry of the glacier, which changed rapidly during the retreat. The flow of water under thick ice is driven by the hydraulic potential gradient,
![]() $\nabla \phi $
, at the glacier bed (Rothlisberger, Reference Rothlisberger1972; Shreve, Reference Shreve1972), which depends on gradients of both the ice-surface elevation, z
s, and the bed elevation, z
b, and on the gravitational acceleration, g, and the densities of ice and water, ρ
i and ρ
w, respectively, such that:
$\nabla \phi $
, at the glacier bed (Rothlisberger, Reference Rothlisberger1972; Shreve, Reference Shreve1972), which depends on gradients of both the ice-surface elevation, z
s, and the bed elevation, z
b, and on the gravitational acceleration, g, and the densities of ice and water, ρ
i and ρ
w, respectively, such that:
(Cuffey and Paterson, Reference Cuffey and Paterson2010). When the slopes of the glacierbed and the ice surface are comparable, the ice-surface slope exerts the dominant control on subglacial water flow (Shreve, Reference Shreve1972). However, when a reverse slope of the glacier bed (rising down-glacier) exceeds that of the equipotential surfaces within the glacier, equivalent to a bed slope of ~11 times the ice-surface slope, subglacial water flow and sediment transport stops. In addition, there is a thermodynamic control on subglacial water flow. Because water traveling along the base of a glacier is at the pressure melting point, the decrease in pressure as the water travels uphill along a reverse sloping bed can cause the water to supercool and refreeze at the base of the glacier if the heat dissipated in the water flow is insufficient to warm the water to the pressure melting point as it ascends along the bed (Rothlisberger, Reference Rothlisberger1972). Refreezing is expected if the bed ascends more steeply than 20–70% of the surface slope (Alley and others, Reference Alley, Lawson, Larson, Evenson and Baker2003). When this condition is met, subglacial sediment transport is expected to vanish or to be severely limited (Hooke, Reference Hooke1991; Alley and others, Reference Alley, Lawson, Larson, Evenson and Baker2003).
Measured glacier-surface profiles and the known bed slope, based on our seismic profiles and as calculated by McNabb and others (Reference McNabb2012), enable us to calculate the subglacial hydraulic potential gradient and refreezing potential as a function of time. We focus on areas of reverse bed slopes to determine how changing ice surface and bed slopes would affect subglacial water and sediment transport during the retreat.
Steeply reverse-sloping beds occur at the down-glacier end of both the inner basin of the fjord and the only major subglacial basin remaining, just up-glacier of the 2013 terminus; these steep sections are centered at down-glacier distances of 54–56 km and 47–49 km, respectively (Fig. 9; Rignot and others, Reference Rignot, Mouginot, Larsen, Gim and Kirchner2013). From 1957 until sometime before 2001, the glacier surface slope over the distal portion of the subglacial basin near 48 km was insufficient to permit stored sediment to escape in the subglacial hydraulic system (Fig. 10). In addition, the steep reverse slopes in both basins are sufficient to promote basal refreezing. Without evacuation, sediment transported in the subglacial system would rapidly accumulate in the subglacial basin, raising the surface of the growing sediment package and decreasing the bed slope until the subglacial sediment could be evacuated (Alley and others, Reference Alley, Lawson, Larson, Evenson and Baker2003). For the major remaining subglacial basin with a length of 3500 m, a depth of ~60 m, and a width of ~500 m, based on estimates from McNabb and others (Reference McNabb2012), sediment accumulating at the mean annual rate of 1.1 × 107 m3 over a period of ~15–20 a would sufficiently reduce the slope of the bed to permit the evacuation of the stored sediment.

Fig. 10. Temporal steepening of the ice-surface slope at three locations near the 2010 terminus (Fig. 9 for locations and data). The ‘km 48’ points trace the steepening trend over the portion of the subglacial basin with a steep reverse slope that acts as a threshold for sediment evacuation from this basin (black horizontal line); below this line the glacier surface is not sufficiently steep for subglacial water to ascend out of the deep subglacial basin and evacuate significant volumes of sediment. We suggest that the sediment output from the glacier increased approximately fivefold between 1995 and 2000, when the glacier surface was steepening rapidly at ‘km 48’ to initiate the evacuation of large quantities of sediment from the subglacial basin directly upvalley of the terminus. The gray box represents 50% uncertainty on the threshold. Surface slopes are calculated over a distance of 1–2 km depending on available data.
We attribute the mid-retreat increase in sediment flux (Fig. 8) to the delayed release of substantial quantities of subglacial sediment facilitated by changes in Columbia Glacier's surface and basal geometry. Such changes include: (1) a steepening of the glacier surface sufficient for the subglacial hydraulic system to evacuate stored sediment, which occurred over the steep reverse-sloping glacier bed as the terminus moved northward during glacial retreat; and (2) a decrease in the reverse bed slope due to continual subglacial sediment accumulation (Figs 9, 10). Our analysis suggests that both these processes occurred in the subglacial basin during the recent period of retreat.
The sediment-flux history, when analyzed in the context of the existing glaciological observations, suggests the importance of the subglacial hydraulic potential gradient and basal refreezing on the delivery of sediment to the fjord. Similarly, the subglacial hydraulic system appeared to control episodic discharges of sediment during surges from Variegated and Bering glaciers, Alaska (Humphrey and Raymond, 1994; Headley and others, Reference Headley, Enkelmann and Hallet2013), and to limit the bedload of Matanuska Glacier, ~50 km northwest of Columbia Glacier (Pearce and others, Reference Pearce2003). Because the sediment flux is influenced by a complex interaction involving the retreat rate and ice flux, the preserved sedimentary record in the fjord is not a simple archive of changes in climate, erosion rate or glacier dynamics. Rather, we suggest that changes in subglacial hydrology can dominate the sedimentary record on a short timescale (years to decades). The tendency for the ice surface to steepen near the terminus over a given area during terminus retreat can cause stored sediments to be rapidly flushed from a subglacial basin. This effect renders the interpretation of the glacimarine sedimentary record challenging, especially over short timescales. Despite these complications, refining the modeling approach developed here will provide the potential to interpret quantitatively, the complex glacial and sediment accumulation histories.
6. SUMMARY AND CONCLUDING REMARKS
We analyzed the sediment accumulation history of Columbia Glacier during its 30 a retreat (1980–2011), leveraging a wealth of glaciological data. Seismic profiles collected throughout the fjord indicate that at least 3.2 ± 1.0 × 108 m3 of sediment accumulated in the newly exposed fjord since 1980 at average rates of 3 × 106 and 19 × 106 m3 a−1 for 1980–1997 and 1998–2011, respectively. We developed a numerical model of the glacier's sediment-flux history to help understand the internal architecture of the sediment package and sediment thickness distribution in the context of the known glacier retreat. In addition to being consistent with the total sediment volume and geometry of the fjord, the modeled sediment-flux history is constrained by glacier-thickness measurements from the boreholes drilled through the glacier in 1987, as well as bathymetric measurements made in 1997 and 2011. Ultimately, this model allows us to relate observations of short-term sediment deposition to the glacimarine sediment record preserved in the fjord.
The modeled sediment-flux history suggests that the sediment load from Columbia Glacier increased fivefold between 1997 and 2000, and that sediments must be transported many kilometers from the ice in order to form the outer basin deposits. Our results also suggest that fjord sediments are likely transported and/or redistributed efficiently by sediment gravity-driven processes close to the seabed to account for the horizontal seabed and approximately parallel internal stratigraphy.
A drainage-basin-averaged erosion rate of at least ~5 mm a−1 is necessary to sustain the observed mean sediment flux over the period of retreat. This effective erosion rate is surprisingly similar to the sediment-production rate necessary to enable Columbia Glacier to advance into its deep fjord on a timescale of centuries to millennia, as calculated by Nick and others (Reference Nick, van der Veen and Oerlemans2007). The similarity between the two independent estimates, which are based on different approaches and data representing different time spans, provides confidence in the long-term erosion rate we obtained for Columbia Glacier.
By combining our calculated temporal variations in sediment delivery with glacier geometry and flow, we show that storage and delayed release of sediment from over-deepened basins beneath the glacier offer a parsimonious explanation for rapid changes in sediment flux; they are not correlated simply with ice flux or retreat rate. In contrast, the timing of these sediment releases is directly linked to when the glacier terminus retreated and the glacier surface steepened significantly near the spill point (or down-glacier lip) of a subglacial overdeepening. The control of the glacier surface and bed geometries, rather than ice flux, on the output of sediment highlights the many factors that affect glacial sediment fluxes over periods of years to decades and that are ultimately reflected in the glacimarine stratigraphic record. This complexity suggests caution should be used when interpreting climate changes and glacial history from short-term glacier-proximal sediment records.
ACKNOWLEDGEMENTS
This work was funded by the Quaternary Research Center at the University of Washington and a NDSEG Fellowship to Boldt Love. Support for glaciological observations and analyses came from the USGS Climate and Land Use Change Mission and the Alaska Climate Science Center. We appreciate Mark Meier and Austin Post for their leading roles in the seminal research on Columbia Glacier and other tidewater glaciers, for developing a comprehensive monitoring program of Columbia Glacier in early anticipation of its retreat, and for providing rich insights and stimulating interest in the complex dynamics of these glaciers. We also thank Dave Janka, captain of the Auklet, for making our field campaign possible and for his deep commitment to understanding the history and environment of Columbia Glacier; Chuck Nittrouer for helping to conceive and support the field work, for lending his coring equipment and for providing insights on an early draft; Dick Sylwester for the use of his seismic equipment; Bob McNabb for collaborating on the glacier bed profiles; Tad Pfeffer and Al Rasmussen for generously sharing their insights; Ethan Welty for providing terminus position information; Shelton Gay for sharing water-column data; Adam Barker and Shaun Finn for help in the field; Lee Liberty for insights and discussions about sonar and seismic data; and Eric Steig for his commitment to supporting ice/ocean studies at the University of Washington. Thoughtful reviews from Martin Truffer, Emily Roland and one anonymous reviewer improved this manuscript. Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government.











