Propagation of a Plastic Wave in Snow

Abstract

When snow is pushed very fast by a moving body a plastic wave is generated at the head of the body. If the velocity of the moving body becomes close to that of the plastic wave, the snow may exert a great resistive force against the body as predicted by Yosida. It is, therefore, very important to study the dynamic behaviour of snow at a high rate of deformation, such as takes place when a snow plough is used on the highway, a train runs on a railroad covered with snow, or an avalanche occurs. Hence, this study is concerned with the safety and maintenance of winter traffic and transportation, and also with the generation and propagation of an avalanche. In order to clarify the detailed processes of the deformation of snow at high rates, laboratory experiments were made by compressing snow at high speed. The propagation of a plastic wave through snow was observed by using a high-speed camera and a pressure-detecting device. Analyses of the data obtained gave the velocity of the plastic wave for various kinds of snow whose density ranged from 0.17 to 0.46 Mg m^-3 and free-water content from o to 17%, whereby studies were made into the dependences on the density and free-water content of the velocity of the plastic wave. When the impact velocity was 4.3 ± 0.2 m s^-1, the wave velocity ranged from 5 m s^-1 for a new snow to 12 m s^-1 for a fine-grained, well-settled snow. The plastic-wave velocity in wet snow was, in general, smaller than that in dry snow of the same density. Changes in density and structure of snow associated with the passage of a plastic wave were studied and discussed. The pressure at the wave front was measured; values of 0.1-0.3 bar were obtained, these are of the same order as the value estimated from theoretical formulae. The plastic-wave velocity was also observed for a confined snow, which showed a larger velocity and plastic strain than an unconfined snow.

Résumé

Propagation des ondes plastiques dans la neige. Lorsque la neige est poussée a grande vitesse par un corps en mouvement une onde plastique est produite en avant de ce corps. Si la vitesse du corps en mouvement devient voisine de celle de l’onde plastique, la neige pent exercer une forte résistance contre le corps comme l’avait prévu Yosida. II est done trés important d’étudier le comportement dynamique de la neige à une grande vitesse de deformation qui se produit lorsqu’on utilise une étrave chasse-neige sur une route, lorsqu’un train parcourt une vole ferrée recouverte de neige, ou dans une avalanche. Done cette étude intéresse la sécurité et is maintenance du trafic hivernal et des transports, ainsi que la production et la propagation d’une avalanche. Pour clarifier les détails des processus des déformations à grande vitesse dam la neige, des experiences ont été faites sur la compression à grande vitesse de la neige. La propagation d’une onde plastique à travers la neige a été observée à l’aide d’une caméra à grande vitesse et d’un dispositif de mesure de pression. Les analyses des résultats obtenus ont donné des vitesses de l’onde plastique dans des neiges de densité allant de 0,17 Mg in^-3 à 0,46 Mg m^-3 avec des teneurs en eau libre de o à 17% les vitesses de l’onde plastique allant de 5 m s^-1 pour une neige fraîche à 12 m s^-1 pour une neige à grains fins bien tassée. La vitesse de l’onde plastique dans la neige humide était en général plus petite que dans la neige séche de même densité. On a étudié et discuté les changements intervenus dans la densité et la structure de la neige à la suite du passage d’une onde plastique. La pression du fond de l’onde a été mesurée; on a obtenu des valeurs de 0,1 à 0,3 bar qui sont du même ordre de grandeur que celics estimées d’aprés les formules théoriques. La vitesse de l’onde plastique a égalgement été observée pour une neige dans un couloir qui a montré une vitesse et une contrainte plus forte que dans une neige de versant.

Zusammenfassung

Fortpflanzung plastischer Wellen in Schnee. Wenn Schnee von einem sehr schnell bewegten Körper gestossen wird, wird eine plastische Welle am Vorderende des Körpers erzeugt. Liegt die Geschwindigkeit des bewegten Körpers nahe bei der der plastischen Welle, so kann der Schnee gemäss den Überlegungen von Yosida dem Körper grossen Widerstand entgegensetzen. Es ist deshalb sehr wichtig, das dynamische Verhalten von Schnee bei hohen Verformungsraten zu studieren, die dann vorkommen, wenn ein Schneepflug auf einer Strasse eingesetzt wird, ein Zug über ein verschneites Geleise fährt oder eine Lawine abgeht. Die vorliegende Untersuchung gilt deshalb der Sicherheit und der Aufrechterhaltung des Verkehrs und Transports im Winter, aber auch der Auslösung und den Wirkungen einer Lawine. Zur detailierten Klärung der Vorgänge bei sehr schneller Deformation von Schnee wurden Laborversuche mit sehr schneller Kompression von Schnee angestellt. Die Fortpflanzung einer plastischen Welle durch den Schnee wurde mit einer schnellaufenden Kamera und einem Druckmessgerät beobachtet. Die Analyse der Daten lieferte die Geschwindigkeit der plastischen Welle far verschiedcne Schneearten, deren Dichte zwischen 0,17 und 0,46 Mg m^-3 und deren Wassergehalt zwischen o und 17% lag; damit waren Studien fiber die Abhängigkeit der Wellengeschwindigkeit von der Dichte und dem Gehalt an freiem Wasser verbunden. Bei einer Aufprallgeschwindigkeit von 4,3 ± 0,2 m s^-1 lag die Wellengeschwindigkeit zwischen 5 m 5^-3 für Neuschnee und 12 ms^-1 für feinkörnigen, gut gesetzten Schnee. Die Geschwindigkeit der plastischen Welle war für nassen Schnee im allgemeinen kleiner als fur trockenen Schnee derselben Dichte. Dichte- und Strukturschwankungen des Schnees, die mit dem Durchgang einer plastischen Welle verknüpft waren, wurden untersucht und diskutiert. Der Druck an der Wellenfront wurde gemessen; es ergab sich ein Wert von 0,1 bis 0,3 bar, dessen Grössenordnung der Abschätzung nach theoretischen Formeln entspricht. Die Geschwindigkeit der plastischen Welle wurde auch in eingegrenzten Schneemassen gemessen; Geschwindigkeit und plastische Spannung waren dabei höher als beim Fehlen einer Eingrenzung.

Introduction

Though extensive studies have been made by many earlier workers on the impulsive compression of snow (Yosida and others, 1957), very few studies have been made into the compression of snow at high deformation rates or into the propagation of the plastic wave in snow. When snow is pushed very fast by a moving body (for example, by a snow plough) a plastic wave is generated at the head of the plough and this propagates through the snow mass. Yosida recently reported that when the moving velocity of the body becomes close to that of the plastic wave the snow may exert a large resistive force against the body (Yosida, 1974[a], 1974[b]). It is, therefore, probable that a high-speed train becomes dangerous if it runs faster than 200 km h^-1 (approximately 60 m s^-1) on a railroad covered with only thin snow when snow is falling. The high-speed removal of snow from a highway may also encounter similar problems. Thus, it is important to study the dynamic behaviour of snow at high rates of deformation bearing in mind the safety and maintenance of winter traffic and transportation in snowy countries. Such a study may also be closely connected with the generation and propagation of avalanches.

The plastic wave in snow was first studied by Napadensky (1964). An explosion was made in a tunnel excavated in polar firn in Greenland and the velocity of the plastic wave thus induced was measured. Her experiment was, however, restricted to an extremely high rate of snow deformation as produced by the explosion, and to a very hard polar firn with a density of 0.55 Mg m^-3. For practical problems in snowy, urban areas, it may be more important to study the propagation of a plastic wave through a snow cover in which the rate of deformation is smaller than the one generated by an explosion, and to study the dependence of the snow density on the plastic-wave velocity.

In order to clarify the dependence of the plastic-wave velocity on the snow density, and to investigate the detailed processes involved in the deformation of snow at high rates, laboratory and field experiments were conducted on the compression of snow, at deformation speeds ranging from 2.5 to 5 m s^-1. The generation and propagation of a plastic wave in snow and the fracturing of snow were investigated using a high-speed camera and a pressure-sensitive device (Sato, unpublished). The data obtained from them were analysed to yield the plastic-wave velocity for various kinds of snow.

Experimental Procedure

Rectangular blocks of snow 200 mm in height and 100 x 100 mm² in top surface area were cut from homogeneous snow layers of a snow pack. On the front surface of each snow block dark lines were marked horizontally at intervals of 20 mm using carbon powder as mark lines for direct observation of the propagation of a plastic wave (Fig. 1). The density of snow ranged from 0.17 to 0.46 Mg m^-3. A cylindrical metal weight of mass 1 kg, guided by thin metal wires, was allowed to fall freely from a height of 2 m above the top surface so that it hit the top surface of the snow block. This impact generated not only elastic waves but also a plastic wave in the snow. Snow fracture often took place when the snow density exceeded 0.3 Mg m^-3. Though an elastic wave is invisible, a plastic wave advancing through the snow can be observed directly as successive displacements of the dark lines marked on the front surface beforehand. Slow-motion ciné pictures were taken at a rate of approximately 4 200 frames per second in order to observe in detail the propagation of a plastic wave through the snow block. The films were analysed by using an automatic film analyser, and the front velocity of a plastic wave was obtained from the successive sudden displacements of the mark lines on the front surface of a snow block as illustrated in Figure 1.

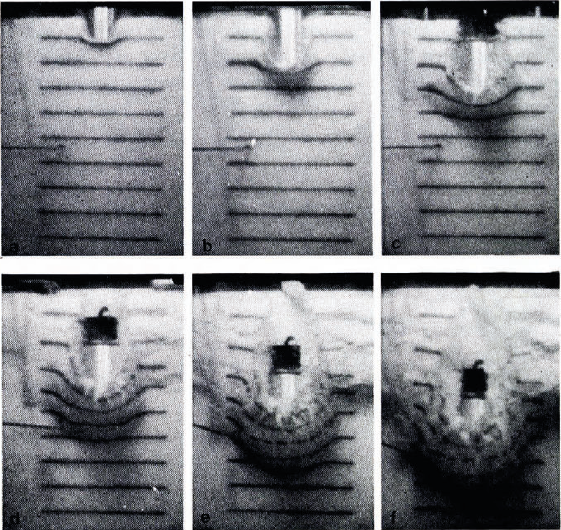
Fig. 1. Propagation of plastic wave in snow. These photographs were selected from frames of 16 mm film at an interval of 5 ms. Dark lines were marked every 20 mm on the snow block.

A pressure-sensitive device was embedded in the snow before the impact in order to estimate the plastic-wave velocity by another method. The pressure change which accompanied the plastic wave-front was detected by this device which was connected to a synchroscope. The plastic-wave velocity obtained by this method was compared with that obtained from the slow-motion film for the same snow sample. We confirmed that the two values agree fairly well with each other. Most of the experiments thereafter were made by using the pressure detection method, because this method is much simpler to carry out than is the film technique.

The experiments for dry snow were made in a cold laboratory maintained at –10°C. For wet snow samples, the free-water content of the snow (mass of water : mass of wet snow) was measured using a combination calorimeter immediately after the impact experiment had finished.

Experimental Results

1. Dependence of snow density on plastic wave velocity

No sooner had the falling weight hit the top surface of a snow block than a plastic wave began to expand downwards. This is clearly seen in the films. As the weight moved downwards through the snow block, the mark lines moved downwards successively at intervals of 2-3 ms. The distance-time curve of the plastic wave propagating through a fine-grained snow of 0.18 Mg m^-3 in density is shown, as an example, in Figure 2 as a thick solid line running through the solid squares. The gradient of this curve gives the front velocity U of the plastic wave in the snow. The value of U in this case is 6.2 m s^-1 for an impact speed of 4.3 m s^-1. The mark lines move downwards, shown by the solid thin curves originating from the solid squares. The gradient of each thin curve gives the particle velocity U of snow immediately after the plastic wave passes it. The value of u decreases slightly with the distance from the struck surface of the snow (as indicated by a numerical value for each curve). The value of u ranges from 4.3 m s^-1 at the upper portion of the snow block, the same value as the impact velocity, to 3.8 m s^-1 at 80-100 mm below the top surface.

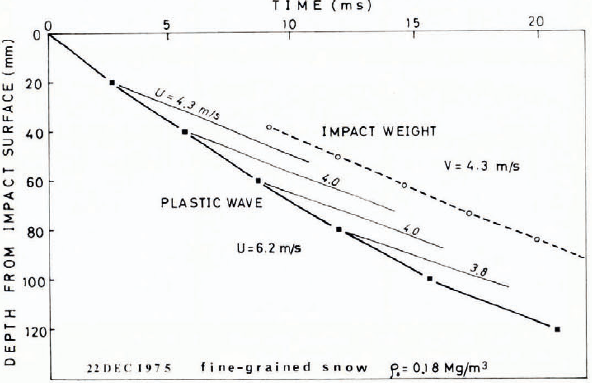
Fig. 2. An example of the distance− time curve of a plastic wave shown by the thick solid line. The gradients of the thin curves and dashed line respectively give the particle velocity and the impact velocity.

Plastic-wave velocities obtained for various kinds of dry snow have been plotted against the snow density using open circles in Figure 3, solid circles represent data for wet snow, and small dots enclosed by a dashed line were those derived from the data of Napadensky.

Fig. 3. Plastic-wave velocity plotted against snow density. Circles denote unconfined snow data; triangles, confined snow. Open and solid symbols respectively for dry and wet snow. The dashed line indicates the relation between plastic-wave velocity and snow density when the density of closest packing of snow particles is taken as 0.6 Mg m^-3. Small dots enclosed by a dashed line are those derived from the data of Napadensky.

Although these plots are widely scattered, it may be seen from this Figure that the plastic-wave velocity U for dry snow increases with the density p _o of snow: for p _o = 0.2 Mg m^-3U is 6.5 m s^-1; for p _o = 0.4 Mg m^-3U is 12 ± 2 m s^-1.

2. Dependence of the plastic-wave velocity on the free-water content of snow

The plastic-wave velocity U was measured for wet snow with various values for the free-water content w (which ranged from 2.6 to 17.7%) using wet snow samples whose density ranged from 0.43 to 0.44 Mg m^-3 cut from homogeneous fine-grained snow layers of a melting snow-pack. The velocity U has been plotted against the free-water content w in Figure 4, and also against the snow density p _o in Figure 3 with solid circles. As shown in these Figures, there is no direct correlation between U and w, but U for wet snow is, in general, smaller than U for dry snow of the same density.

Fig. 4. Plastic-wave velocity plotted against free-water content of snow.

3. Changes in density and structure of snow caused by the impact

Thin sections of thickness to mm were cut out from a snow block after each impact so that structure changes of the snow caused by the impact could be examined. Observations made under transmitted light showed that the snow immediately below the indented weight was heavily compacted by the impact (as illustrated by region A in Fig. 5a). The underlying snow (region B in Fig. 5a) seems to remain unchanged.

Fig. 5. Thin slice cut from a snow block after the impact. Heavily compacted portion “A" and unchanged portion “B”. b and c. Vertical thin sections cut from the boundary between “A" and “B”, and from “B”, respectively.

Immediately after the impact, the density of snow was measured at to mm intervals throughout the snow, which originally had a density of 0.30 Mg m^-3. The density of the heavily compacted portion was found to be much larger than that of the original snow as seen in Figures 5b and c, but it decreased from 0.61 Mg m^-3 at the top down to 0.49 Mg m^-3 at the bottom of this portion. The density of snow in the underlying portion (region B) was, however, equal to the original density. This means that the structure and the density of the underlying snow were not influenced by the impact at all.

Discussion

When a plastic wave is moving through snow, the density of the snow should be increased abruptly by the arrival of the wave-front. Since the pressure p in the snow and the particle velocity u of the snow are both zero before the arrival of the wave-front, the following formulae can be derived from the conservation of mass and momentum of the snow

(1)

(2)

where p _o and p ₁ are the density of snow before and immediately after the passage of the plastic wave-front respectively. These are well-known Rankine-Hugoniot relations for the plastic wave.

The density p ₁ of snow at the wave-front was calculated by using Equation (1) for various snow samples with different densities. For instance, p ₁ = 0.50 ± 0.05 Mg m^-3 for snow with p ₀, = 0.18 Mg m^-3; p ₁, = 0.55 ± 0.03 Mg m^-3 for p _o = 0.24 Mg m^-3. For a higher density snow (p = 0.3 Mg m^-3), the calculated value of p ₁ generally exceeds 0.8 Mg m^-3 or even attains 0.917 Mg m^-3, i.e. the density of ice. This is, however, most unlikely to occur in snow.

It is well known that the density of snow at the closest packing of snow grains is approximately 0.6 Mg m^-3. To exceed a density of 0.6 Mg m^-3 it is necessary to compress the snow to allow the plastic deformation of snow grains to occur. It is, therefore, almost impossible to turn the snow into ice instantly except when an extremely large stress, such as is caused by an explosion, is applied to snow. Even when a snow block is compressed under a fairly large stress such as 10 bar, it takes a long time to transform the snow into ice. This means that the density associated with the plastic wave-front cannot exceed the density of snow at the closest packing: ρ ₁ = 0.6 Mg m^-3.

It may, therefore, be assumed that when the value of p ₁ exceeds 0.6 Mg m^-3 macroscopic fracturing would occur at the wave-front and propagate through the snow block. Such macroscopic fracturing was very often observed to run through the entire snow block at the time of impact; the snow density was greater than 0.3 Mg m^-3. For lower density snow (new or lightly settled fine-grained snow), on the other hand, macroscopic fracturing was never observed in the experiments. These experimental facts strongly support the above assumption as to the initiation of macroscopic fracture as the wave-front passes.

Equation (1) can be rewritten as

(3)

This formula shows that the plastic-wave velocity becomes larger when the impact velocity u is larger or the initial snow density p _o approaches p _o the density of snow at the closest packing. If p _o equals p ₁, U becomes infinite.

In the experiments, the impact velocity u was taken as 4.3 ± 0.2 m s^-1, so that the plastic wave velocity U is a unique function of the initial snow density p _o, provided that p ₁ is fixed at a constant value such as 0.6 Mg m^-3. The curve drawn as a dashed line in Figure 3 indicates the relation between U and p _o when p₁ = 0.6 Mg m^-3. Though the observed values are widely dispersed, it may be said that they tend to fit the predicted curve.

If a similar experiment is carried out on a confined snow sample with a density higher than 0.3 Mg m^-3 which is prevented from sustaining any macroscopic fracture at the time of impact, it may indicate whether this assumption is reasonable or not. So, a snow block in cylindrical form, 60 mm in diameter and 300 mm in height, was confined laterally by an acrylic tube and was hit strongly on the top surface by an iron hammer with an impact velocity of 2.5 m s^-1. Heavy compaction occurred in the snow block, but macroscopic fracturing was not observed.

The plastic-wave velocity and the plastic strain in the snow were obtained from an analysis of the slow-motion 16 mm pictures taken. The distance-time graph of the plastic wave and the plastic strain obtained for dry snow of 0.37 Mg m^-3 density are shown by a thick and a thin solid curve respectively in Figure 6a. The impact weight was prevented from further movement by a stopper when the weight had reached a level of 25 mm from the initial top surface of the snow block. This level was taken as the origin of the ordinate (Z-axis) of this Figure. The plastic-wave velocity was, in general, much larger than those obtained for unconfined snow; it was 38.7 m s^-1 in the upper part of the snow block from Z = o to Z = 65 mm but fell to 14.1 m s^-1 in the lower portion.

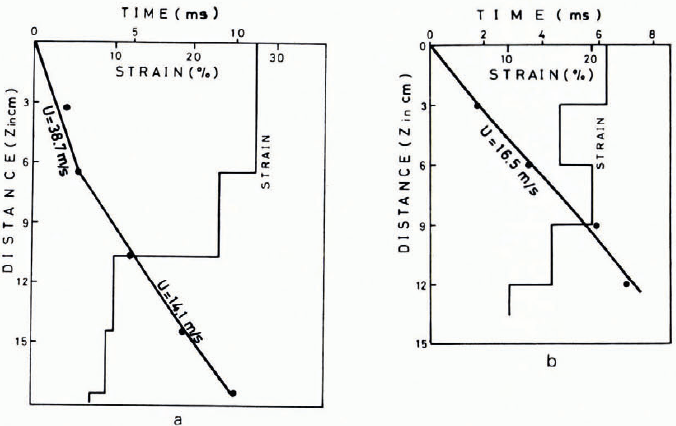
Fig. 6. Thick solid lines give the distance− time curves for confined snow. Thin solid lines give plastic strain for different levels. a, dry snow (p_o = 0.37 Mg m^-3); b, wet snow (p_o = 0.46 Mg m^-3).

In this experiment a large plastic strain extended further down in the snow block from the impact head; this is in strong contrast to the experiments with unconfined snow. In the unconfined snows, plastic strain was found to extend only 30-50 mm immediately beneath the impact weight, and any plastic strain or densified snow was not observed in the underlying snow layers.

The final density p _f of the lower portion of the confined snow, calculated by converting the observed plastic strain, was 0.41 Mg m^-3 between Z = 105 and 180 mm. The predicted value of p ₁ derived from Equation (1) is 0.45 Mg m^-3 for this region. This suggests that the density of snow at a propagating wave-front in a confined dry snow does not always exceed the snow density at the closest packing, and also indicates that the density is reduced after the passage of the plastic wave-front.

This is not the case for a confined wet snow. Impact was made on wet snow samples in an acrylic tube. One of the results obtained for a snow of 0.46 Mg m^-3 in density and 15% in free-water content is illustrated in Figure 6b. The plastic-wave velocity was 16.5 m s^-1 from the top down to Z = 150 mm. The final density ρt derived from the observed plasticstrain was 0.56 Mg m^-3 in the upper part, which reduced to 0.51 Mg m^-3 in the lower portion. The predicted value of pi obtained from Equation (1) is 0.55 Mg m^-3. Thus, both values of ρ_t and ρ_t, attained the closest packing density of snow. Similar results were also obtained for another wet snow sample. This fact may be explained as follows: wet snow is much weaker than dry snow of the same density, and, when the plastic wave is passing by, snow grains with weakened or broken grain bonds are easily compacted due to easy gliding between neighbouring snow grains which are covered with water films.

The pressure P₁ associated with the plastic wave can be estimated from Equation (2). The value of P₁ is given by substituting the observed values of the plastic-wave velocity U and the impact velocity u together with the initial density of snow ρ_o into Equation (2). The value of P₁ thus obtained ranges from 0.05 to 0. I bar for unconfined snow, and 0.1 to 0.25 bar for confined snow. These values of pressure were compared with those obtained from direct measurements. A pressure-measuring device (a strain gauge) was embedded in snow and the pressure P₁ was obtained directly. The observed value of P₁ ranged mostly from 0. 1 to 0.3 bar for unconfined snow. Though the observed values are two to three times larger than those estimated from the theoretical formulae, the order of magnitude of the pressure was established. Since the compressive strength of the snow is 0.1 to 0.3 bar, breaking of ice bonds between snow grains or microscopic fracturing of snow could occur at the arrival of the plastic wave-front.

Concluding Remarks

Only a few experimental studies have so far been made on the deformation of snow at high deformation speeds. Napadensky (1964) made extensive studies into the propagation of a plastic wave in snow; she measured the velocity of the plastic wave as a function of the impact velocity. Since most of her experiments were conducted on Greenland snow, the results were restricted to a very hard firn whose density exceeded 0.5 Mg m^-3, and so no relation between the plastic-wave velocity and the density of snow was obtained in her experiments.

In the present study, detailed processes of the generation and the propagation of a plastic wave were observed for different kinds of snow; namely, from a new snow of 0.17 Mg m^-3 in density to a fine-grained well-settled snow of 0.46 Mg m^-3 comprising dry and wet snow of from o to 17% in free-water content. The velocity of a plastic wave in snow was obtained by analysing slow-motion pictures and also from data obtained by a pressure measuring device at the time of impact. Dependences of the density and free-water content of snow on the plastic-wave velocity were studied for these different kinds of snow in both confined and unconfined states. Changes in density and structure of snow associated with the passage of a plastic wave were studied and discussed in connection with the pressure at the wave-front. Though these studies were made to clarify the dynamic behaviour of snow at a high rate of deformation, the range of the impact velocity, and hence the plastic-wave velocity, was rather small (from 2.5 to 5 m s^-1). Further experimental studies are under way for the impact velocity range 5 to 15 m s^-1. The results will be published in the near future.