Introduction
Snowflakes undergo changes in shape shortly after deposition even though the air temperature may be well below the melting point. The initial stage of this metamorphism consists of the rounding of the sharp edges of the flakes due to evaporation from convex surfaces. This is followed by the break-up of individual flakes into a number of isolated grains, so that there is a decrease in the average size of the particles. As the particles decrease in size the snow undergoes partial collapse which produces a more efficient packing of’ the grains. At points where the grains are in contact, ice bonds or necks begin to grow by sintering, and the strength of the snow increases with time. Simultaneously, the grains tend to become more uniform in size, for the smaller ones evaporate and lose their mass to the langer grains. The time required for dry snow to transform into this weakly cohesive aggregate of rounded grains increases with decreasing temperature; at −5°C. it takes a matter of weeks.
The growth of ice bonds between spherical particles of ice held at temperatures below their melting point, has been investigated in recent years by a number of workers (Reference KingeryKingery, 1960; Reference KuroiwaKuroiwa, 1961; Reference Hobbs and MasonHobbs and Mason, 1964). The driving force for the transfer of material to the neck between two particles is provided by the gradient in chemical potential existing between the highly stressed region beneath the concave surface of the neck and points elsewhere in the system. Under the influence of this force, molecules can move to the neck by four mechanisms: transfer via the vapour phase, volume diffusion through the ice, surface diffusion over the ice, and plastic or viscous flow. These four mechanisms are not, of course, mutually exclusive, each contributes to the growth of the neck to a greater or lesser extent. Hobbs and Mason (1964) made theoretical estimates of the contributions to the neck growth between two ice spheres from each of these four mechanisms, and concluded that the transfer of material to the neck by the diffusion of water molecules through the air should be the dominant mechanism. The growth of the neck by volume diffusion and surface diffusion was estimated to be smaller than the dominant mechanism by about four orders of magnitude. Measurements of the rate of growth of the neck between two ice spheres were found to be in good agreement with this theory. More recently, Reference HobbsHobbs (1965) has shown that the theory can also account for the observed time dependence of the strength of firn.
Probably the most striking phenomenon associated with the metamorphism of snow is the increase in density. Freshly fallen snow has a density in the range 0.01 to 0.25 g. cm.−3; the rounding of the flakes followed by grain packing can increase the density to a maximum value of 0.58 g. cm.−3 (the critical density), which corresponds to close random packing of the grains (Reference Anderson, Benson and KingeryAnderson and Benson, 1963). For old snow at a uniform temperature further increases in the density must occur by the mutual interpenetration of the grains at their points of contact. Now it is clear that although the growth of the neck between two grains of ice may be dominated by the transfer of material through the air, this mechanism cannot contribute to the densification of old snow since it does not produce any change in the distance between the centres of the grains. Similarly, the transfer of material to the neck by surface diffusion will not affect the density of old snow. The movement of material to the neck by volume diffusion, however, will produce a decrease in the distance between the centres of two grains and this mechanism will therefore give rise to densification. As the pressure of the overlying snow increases, a point will eventually be reached where visco-plastic flow occurs and this may then dominate the densification process.
This paper is concerned with a theoretical and experimental study of the densification of old snow in the absence of temperature gradients and prior to the onset of visco-plastic flow due to overburden pressure. We derive first a theoretical expression for the rate of increase in the density of a spherical compact of ice spheres due to volume diffusion at the points of contact between the spheres. An experimental technique which allows accurate measurement of the changes in density of a sample of ice spheres is then described, and the results of a series of measurements on the densification of compacts of these spheres are presented. Finally, the experimental results are compared with the predictions of our theoretical model.
Theory
We consider first the sintering of two isolated spherical particles of ice which have the same radius r (Fig. 1). If the neck between the two particles is assumed to grow predominantly by the transfer of material through the vapour phase, the radius x of the neck after time t is given by (Hobbs and Mason, 1964):

where γ is the surface tension, δ the intermolecular spacing, α the condensation oefficient, β the density, m the mass of a molecule, and L s the latent heat of sublimation of ice, p 0 the equilibrium vapour pressure of ice at temperature T, and D G and K are respectively the diffusion coefficient of water vapour in air and the thermal conductivity of air at temperature T; k is Boltzmann’s constant. For simplicity Equation (1) may be written as
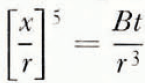
where B is a temperature-dependent term given by


Fig. 1. The, geometry of two sintering spheres
Experimental measurements (Hobbs and Mason, 1964) of the radius, temperature, and time dependence of the growth of the neck between two ice spheres, 25 μm. to 350 μm. radius, in the temperature range −3° to −20°C. are found to be in good agreement with Equation (1). The absolute size of the neck at time t is also given by equation (1) if the condensation coefficient α is taken as 0.2.
The transfer of molecules by volume diffusion through the ice lattice to the surface of the neck between two particles is caused by a gradient in the concentration of vacancies. It is well known that the equilibrium concentration of molecules in the vapour phase is less above a concave surface than above a plane surface, the difference being given by Kelvin’s equation. Similarly, the equilibrium concentration of vacancies C ρ just beneath a concave surface is greater than that beneath a plane surface C 0. In this case C ρ is related to C 0 by an expression analogous to Kelvin’s equation, namely

where the curvature of the neck has been taken as 1/ρ since, except at the very initial stages of sintering, x≫ρ. Approximating the exponential in (4) yields

Due to this difference in concentration of vacancies, molecules will diffuse from the interior of the neck to the surface. Hence, the distance between the centres of the two spheres will gradually decrease due to the continual collapse of the spheres over their area of contact.
To calculate the rate of change of the distance between the centres of two spheres, it is necessary to determine the mass of material that diffuses to the surface by volume diffusion. The number of vacancies,
where A is the surface area of the neck, D the diffusion coefficient for vacancies and grad C the gradient of vacancies. The precise path which the vacancies take is not known with certainty. However, we may assume that the grain boundary between the two spheres acts as an efficient sink for the vacancies and that the concentration of vacancies at a grain boundary is the same as that at a plane surface C 0. The distance over which the concentration of vacancies falls from its value C ρ at the surface of the neck to C 0 will be taken as aρ where a is a constant of proportionality. If the neck is considered to be a cylinder of radius x and height 2ρ, the surface area is A = 4πxρ. Equation (6) may therefore be written as
or

Hence, if V′ is the total volume of material that has moved to the surface of the neck by volume diffusion through the ice after time t,

where D v = DC 0 δ 3 is the volume self-diffusion coefficient for water molecules in ice and δ 3 has been taken as the volume of a vacancy. Provided x/r is not too large, we have from the geometry of the system ρ = x 2/4r, and the volume of the double spherical cap of height y is V′ = 2πy 2 r. Therefore

Combining Equations (2) and (10) and integrating gives

where 2y is the change in centre-centre distance between two spheres after they have sintered together for time t.
We turn now to the densification of a compact of uniform ice spheres due to volume diffusion. For simplicity a spherical compact will be considered. If the initial volume and radius of the compact are respectively V and R, and these quantities diminish by amounts ΔV and ΔR in time t,

If there are n spheres of radius r in the length R,
or, for large n
Therefore,
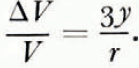
From equations (11) and (14),

This theoretical expression for the change in the volume of a spherical compact of ice spheres by volume diffusion, can be checked experimentally in the following ways. First, Equation (15) predicts that a log-log plot of ΔV/V against t should be a straight line of slope 2/5. Secondly, at a fixed temperature, a log-log plot of r against the time required to produce a given value of ΔV/V should be a straight line of slope 1/3. However, the magnitude and temperature dependence of ΔV/V cannot be predicted from Equation (15) since the magnitude of the proportionality constant a and its variation with temperature are not known.
Experimental Techniques
Compacts containing approximately 105 ice spheres of uniform size were required for the densification measurements. The apparatus used for producing the ice spheres is shown in Figure 2. Water droplets were produced by directing an axially symmetrical jet of air along the outside of a hypodermic needle through which water was passed under slight pressure. The air jet caused the water to be blown off the needle in the form of a single stream of fairly uniformly sized droplets. The stream remained stable for the required period of five to seven hours necessary to collect a test sample. By changing the pressure-head of water and the velocity of the air jet the diameters of the droplets could be varied from about 200 to 1000 μm. The droplets were frozen in free fall by passing them through a very cold tower which was refrigerated by cold air. The frozen droplets were caught at the base of the tower in a flask containing liquid nitrogen.

Fig. 2. Apparatus for producing uniform ice spheres
After the required number of droplets had been collected they were transferred to a cold room and sized by washing them with liquid nitrogen through a set of standard sieves. This process removed the badly fractured spheres, ice fragments and aggregates. The particles removed as undersized were usually less than 3 per cent of the original volume, while the oversized particles amounted to about 5 to 10 per cent. Direct measurements on the sizes of the remaining spheres showed that more than 85 per cent of them were within 10 μm. of the mean size, although a few of the remaining 15 per cent differed by as much as 50 μm. from the mean diameter. After the spheres had been sorted and sized they were returned to the liquid nitrogen for storage. No bonding between the ice spheres could be detected when they were stored in this way.
The method for measuring the change in volume of a compact of the ice spheres with time had to satisfy several stringent requirements. lt needed to have a sensitivity of not less than 0.1 per cent of the total volume of the compact. Since the compacts that were used had volumes of about 500 cm.3, this meant that changes in volume of 0.5 cm.3 had to be measurable. Moreover, the compact had to be sealed in order to prevent net evaporation losses to the air, and had to be kept at a uniform temperature. An ideal method was eventually developed which satisfied all these requirements. Prior to the use of this method, however, two other techniques were tried which yielded some results. Since we will need to refer later to some of these early results, a brief description will first be given of these two methods, and the final method that was employed will then be described in detail.
In the first method that was tried the ice spheres, together with some auxiliary weights, were poured into an uninfiated neoprene weather balloon until the skin of the balloon drew tightly around the compact. The balloon was then immersed in a refrigerated bath of kerosene and attached by means of a long thin wire to a sensitive analytical balance. The changes in the volume of the compact could then be deduced from the changes in its apparent weight. This simple device was, in principle, very accurate. With a compact of total volume 300 cm.3, consisting of spheres 400 μm. in diameter, a change of 10−2 μm. in the distance between the centres of pairs of spheres could be detected. It was found, however, that on some occasions small amounts of kerosene had penetrated into the interior of the balloon. In an effort to eliminate this serious source of error, the kerosene was replaced first by an automotive oil and then by a low viscosity Arctic motor oil. These fluids were noticeably less diffusively penetrating than kerosene, but since the possibility of some penetration of the fluid through the walls of the balloon could never be completely eliminated this method was finally abandoned.
The second method that was tried utilized a modified version of the Beckman gas pychnometer. This instrument consists of a pair of identical piston-compression cylinders which are connected by a differential pressure gauge. The ice spheres were again placed into a neoprene balloon which was put into one of the cylinders. The other cylinder was constructed so that at the extreme inward travel of its piston the entrapped air was corn-pressed to an overpressure of one atmosphere. The volume of the compact could be determined by compressing the cylinder in which it was contained to the same overpressure as the other cylinder, and measuring the corresponding distance of traverse of its piston. By simultaneously pressurizing both cylinders at the same rate, thus eliminating failure of the gas law, and by taking repeated measurements, the volume of the compact could be determined to within 0.cm.3. Unfortunately, this method had to be abandoned owing to repeated mechanical failures of the instrument at low temperatures.
The above two techniques served to demonstrate the accuracy that could be obtained in measuring the changes in volume of the compact by means of a displacement method. The final method that was adopted was therefore of the displacement type, but it avoided the difficulties of the two earlier methods and was more accurate. The compact of ice spheres was again contained in a neoprene weather balloon. The undistended volume of the balloon was less than the volume of the compact so that the balloon gripped the compact and conformed accurately to its surface contours (Fig. 3). In order to fill the balloon, the ice spheres were placed in a plastic bottle which was fitted at its base with a three-way stopcock. The balloon was fastened to the neck of the bottle, inflated slightly, and then filled with the spheres by inverting the bottle. After the excess pressure in the balloon was released, the balloon was sealed. The apparatus for measuring the changes in the volume of the balloon with time is shown in Figure 4; we shall call this instrument the mercury dilatometer. It consists of a large aluminium container fitted with a 1 mm. diameter glass capillary tube and a reservoir with piston. This apparatus was placed in a large cold chamber and, after placing the sealed balloon in the container, the top was bolted down. The reservoir was then filled with mercury and with the aid of the piston the mercury was forced into the container and up to a certain level a in the capillary tube. As the compact densified the mercury level in the capillary tube would drop to some level b, a few centimetres below a, at which time the mercury level would be returned to a. By measuring the volume of the capillary tube between points a and b the magnitudes of the changes in volume of the compact in given intervals of time could be obtained. The instrument was made semi-automatic by placing a photo-diode and peanut bulb across the capillary tube which would sound an alarm whenever the mercury level fell below b. To minimize temperature fluctuations, the aluminium container was placed in contact with about 50 kg. of aluminium in the cold chamber. The large heat capacity of this mass helped to keep the temperature of the sample constant to within a few tenths of a degree. Changes in the volume of the compact of 1 part in 105 could be measured easily with this apparatus; improvements in the accuracy of measuring the levels at a and b could have increased the sensitivity by an order of magnitude, but this was not necessary for our measurements.

Fig. 3. A portion of the balloon. The black spots are bumps made by the ice spheres immediately beneath the surface. Full size

Fig. 4. The mercury dilatometer
The mercury dilatometer provided direct experimental data on the rate of change in the volume of a spherical compact of ice spheres at different times. Stepwise summation of these data gave ΔV as a function of time t, and these results could be used to check the validity of Equation (15).
Experimental Results
The initial densities of the compacts were about 0.55 g. cm.−3, indicating that the arrangement of the spheres was not far removed from close random packed. The experimental results showed that the compacts underwent small but significant changes in density with time. For example, with 600 μm. diameter spheres at −10°C., the density increased by approximately 2 per cent after 1000 min. of sintering. Details of the experimental results are given below.
Time dependence
Log-log plots of ΔV/V as a function of time for different sizes of ice sphere and different temperatures are shown in Figures 5, 6 and 7. All of the experimental results lie on a series of straight lines with very little experimental scatter. The two separate runs at −9.6°C. and −10.0°C. on spheres 370 μm. in radius, shown in Figure 5, illustrate the reproducibility of the data. For temperatures between −7° and −20°C. the average slope of the log (ΔV/V) against log t results is 0.39. However, the slope is definitely dependent on temperature, for it increases from about 0.25 at −2.5°C. to about 0.42 at −15°C. Below −15°C. the slope remains approximately constant.

Fig. 5. Effect of radius of spheres on densification as a function of time

Fig. 6. Effect of temperature on densification as a function of time

Fig. 7. Effect of temperature an densification as a function of time
Size dependence
Figure 5 illustrates the effect on the densification of changing the radius of the ice spheres. It can be seen that at the same temperature a compact of smaller spheres densifies by a greater amount in a given time than does a compact of larger spheres. This effect is displayed in a different form in Figure 8 where log r is plotted against the logarithm of the time required to reach a given value of ΔV/V. The slope of the line through the three experimental points is 0.29.

Fig. 8. Effect of radius of spheres on time required to reach a given value of ΔV/ V
Magnitude of the densification and its variation with temperature
Rearrangement of Equation (15) gives

From the measured values of ΔV/V, t and r, and the known values of the other parameters on the right-hand side of Equation (16), values may be calculated for D v/a as a function of temperature. This quantity gives a measure of the magnitude of the densification. The results are shown in Figure 9 where log (D v/a) is plotted against 1/T On this plot the experimental results lie roughly on a straight line, which indicates that

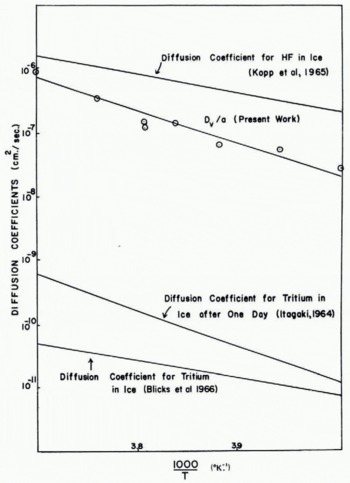
Fig. 9. Comparison of measurements of D v /a from present work with volume diffusion coefficients in ice measured by other techniques
The magnitude of D v/a at −13°C. is about 10–7 cm.2/sec. and the experimental value of E is approximately 20±2 kcal./mole.
Pressure dependence
The results described above were all obtained using the mercury dilatometer. In this device the compact is under a small hydrostatic overpressure of about 18 in. (46 cm.) of mercury, and it is possible that this pressure could affect the densification. To see if this was the case an experiment was carried out in which the height of the mercury in the capillary tube was initially 9 in. (23 cm.), after a period of time this was increased to 18 in. (46 cm.) and subsequently to 27 in. (69 cm.). These changes in the applied overpressure produced no detectable change in the densification of the compact.
Another check which can be made to see whether or not the overpressure affects the densification, is to compare the results obtained with the mercury dilatometer with those obtained from the other two devices described in the last section. The overpressure in the oil-immersion technique was only about 0.3 in. (8 mm.) of mercury whilst in the Beckman Gas Pychnometer the compact sintered at zero overpressure, although this was raised momentarily to one atmosphere when measurements were taken. In Figure 10 some measurements from these three instruments are compared. It can be seen that in the range 0.3 in. (8 mm.) to 18 in. (46 cm.) of mercury, the densification is not changed significantly by the overpressure.
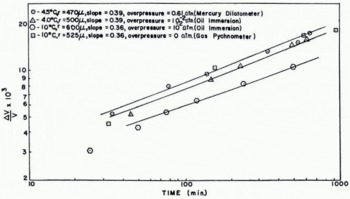
Fig. 10. Effects of overpressure on densification as a function of time
Effect of environment
A few experiments were carried out in which compacts were first allowed to sinter for a certain time in air, and then the ice spheres were covered with silicone oil. Subsequent measurements on the densification of the compact did not reveal any significant changes in the rate of densification, although the measurements in this case were not nearly as accurate as those in air.
Discussion of Results
The average value of the exponent for the time dependence of the densification found experimentally, namely 0.39, is in excellent agreement with the value of 0.4 predicted by Equation (15). However, the observed variation of this exponent with temperature is not predicted directly by our theory. This variation can be explained if the value of the exponent for the time-dependence of the neck growth between two spheres increases with increasing temperature. For example, if instead of x ∝ t 1/2 in Equation (2) we write at high temperatures x ∝ t 1/4, then ΔV/V ∝ t 3/8 instead of t 2/5 This explanation is supported by the fact that in experimental measurements on the growth of the neck between two ice spheres, Reference KuroiwaKuroiwa (1961) found that there was a tendency for the magnitude of the exponent of t to increase with increasing temperature. It should be borne in mind, however, that the experimental measurements at higher temperatures show more scatter than those at lower temperatures and are therefore less reliable.
Equation (15) predicts that a graph of log r against the logarithm of the time required to produce a given value of ΔV/V should have a slope of 0.33. This is in good agreement with the experimental slope of 0.29 (Fig. 8). However, it should be noted that the experimental value is based on just three experimental points, although these are separated by two orders of magnitude on the time scale.
If the experimental values of ΔV/V are substituted into Equation (15), the variation of D v/a with temperature may be deduced. The results are shown in Figure 9 where they are compared with some independent measurements of the volume diffusion coefficient Dv obtained by different workers. Reference KoppKopp and others (1965), using nuclear magnetic resonance techniques, found the activation energy of D v for the diffusion of HF in ice to be 13.4±1.8 kcal./mole. Reference BlicksBlicks and others (1966) obtained an activation energy for D v of 14.4±0.7 kcal./mole for the diffusion of tritium in ice. Reference ItagakiItagaki (1964) also used tritium as a tracer and found that the activation energy of D v was time-dependent, after one day it was 24.2 kcal./mole and after seven days 15.7±2 kcal./mole. In general, therefore, our experimental value of 20±2 kcal./mole for the activation energy of D v/a is larger than the activation energies that have been measured for D v. This difference could be due to the temperature dependence of the factor a.
In order to check if the absolute magnitudes of D v/a deduced from the densification measurements are reasonable, it is necessary to know the value of the proportionality constant a. Unfortunately, the magnitude of this quantity is a matter for speculation. In the original work on the sintering of ceramic and metallic particles Reference KuczynskiKuczynski (1949) assumed that the value of a was unity; the true value, however, could well be as small as 10−2, corresponding to a diffusion length of a few hundred molecular layers. If we accept a value of unity for a, it would appear at first glance that our experimental values for D v are about three orders of magnitude larger than those obtained from radioactive measurements. However, it should be noted that the present results were obtained using ice spheres which were very polycrystalline, whereas, the radioactive measurements were made on single crystals of ice. Diffusion coefficients for polycrystalline specimens are commonly found to be an order of magnitude larger than those for single crystals of the same material. Moreover, Reference ItagakiItagaki (1964) found that at short times (less than 1 day) the diffusion coefficient of tritium in ice may have a value almost an order of magnitude larger than the value measured after ten days. Finally, it is interesting to note that the magnitudes of the diffusion coefficient of hydrogen fluoride in ice measured by Reference KoppKopp and others (1965) lie quite close to our experimental values of D v/a.
Independent estimates of the value of D v/a were obtained by measuring the rate of growth of the neck between two ice spheres completely immersed in silicone oil. Under these conditions the neck cannot grow by the transfer of material through the environment, and volume diffusion should therefore provide the main contribution to the growth of the neck. Two ice spheres were placed gently in contact in air and allowed to sinter together for a short time. Silicone oil was then poured over the spheres and measurements on the growth of the neck were continued. Due to the difficulties of making accurate measurements of the size of the neck through the silicone oil, the results showed considerable scatter. Nevertheless, the neck continued to grow in the silicone oil but the time required to reach a given value of x/r was increased by about an order of magnitude over the corresponding time in air. Similar results to this were obtained by Reference KuroiwaKuroiwa (1961) and Reference Hobbs and MasonHobbs and Mason (1964) for the sintering of ice spheres in liquid kerosene. It is interesting to note that Hobbs and Mason found that when two ice spheres were immersed in silicone oil and then pushed into contact, no neck growth took place. This must have been due to the fact that actual physical contact of the two spheres never occurred, presumably due to the presence of a thin layer of silicone oil between them. Assuming that in the presence of silicone oil sintering occurs by volume diffusion alone, the value of D v/a is found to be about 10−8 cm.2/sec. at −10°C. It can be seen from Figure 9 that this value is about an order of magnitude smaller than that deduced from the densification experiments, however, it does provide experimental confirmation that the magnitudes of D v/a are considerably higher than might have been expected.
The observed decrease in the rate of neck growth between two spheres in silicone oil, corresponds to a reduction of about one order of magnitude in the value of B in Equation (2). Hence, the densification of a compact of ice spheres in silicone oil should be given by the same expression as that in air, namely Equation (15), except the value of B will be one-tenth that in air and the surface tension r will be reduced by about 20 dyne/cm. These changes make the densification after a certain time in silicone oil about 0.7 that which would have taken place in air. This is a small difference and accounts for the fact that no difference could be detected between the amounts of densification in air and silicone oil.
The high values of D v/a found in this work indicate that the contribution to the neck growth between two spheres due to volume diffusion cannot be ignored. The values of D v/a deduced from the densification measurements are comparable to the values of the transport coefficient for transfer through the vapour phase deduced by Reference Hobbs and MasonHobbs and Mason (1964). This would imply that volume diffusion and transfer through the vapour phase contribute equal amounts to the growth of the neck between two ice spheres situated in air. However, the fact that the neck growth is found to be an order of magnitude less in silicone oil than in air, suggests that in air transfer through the vapour phase dominates volume diffusion by about an order of magnitude. It should be emphasized that the use of Equation (1) in deriving the expression for the densification of a compact of ice spheres, relies only on the empirical correctness of this expression and not on its theoretical foundations.
In summary, the theory and experiments described in this paper indicate that volume diffusion in ice can play an important role in the metamorphism of dry snow. Densification by volume diffusion alone can increase the density of dry snow beyond the critical value for a close random packed array of spheres, and this mechanism can proceed in the absence of any temperature gradients or overburden pressure.
Acknowledgements
This work has been supported at various times by the following grants to the University of Washington: N.A.S.A. Grant NsG-484 entitled “Multidisciplinary Research on the Nature and Properties of Ceramic Materials”; NSFGP-2971 and NSFGP-3809 from the Atmospheric Sciences Section of the National Science Foundation.











