Introduction
The sedimentological characteristics of glaciological landforms can offer valuable insights into their mode of formation and the origin and transport history of the material involved (Reference BoultonBoulton, 1978; Reference Eyles and RogersonEyles and Rogerson, 1978; Reference HaldorsenHaldorsen, 1981; Reference McLaren and BowlesMcLaren and Bowles, 1985; Reference Brodzikowski and Van LoonBrodzikowski and Van Loon, 1987; Reference ShawShaw, 1987; Reference Hooke and IversonHooke and Iverson, 1995; Reference Knight, Patterson, Waller, Jones and RobinsonKnight and others, 2000). Grain-size frequency distribution data describe the relative amount, by mass or volume, of particles according to their size in a sample, and are often combined with observations of clast fabric and descriptions of clast shape to describe the lithofacies under investigation (e.g. Reference Hambrey and GlasserHambrey and Glasser, 2012). Grain-size information has been demonstrated to be of significant value for the reconstruction of basal-ice characteristics and the thermal and dynamic properties of former ice masses (e.g. Reference Knight, Patterson, Waller, Jones and RobinsonKnight and others, 2000). Grain-size information has also been used to interpret styles and magnitudes of deformation in glacial sediments (e.g. Reference Hooke and IversonHooke and Iversen, 1995; Reference Iverson, Hooyer and HookeIverson and others, 1996; Reference Fischer and HubbardFischer and Hubbard, 1999); quantify rates and patterns of weathering in glacierized catchments (e.g. Reference AndersonAnderson, 2005) including the modification of rockfall deposits onto glaciers (Reference Shugar and ClagueShugar and Clague, 2011); quantify the thermal conductance properties of supraglacial debris and its influence for modelling sub-debris ablation (e.g. Reference Nicholson and BennNicholson and Benn, 2012); and reconstructing the sediment transport competency of glacial outwash flows (e.g. Reference Cudden and HoeyCudden and Hoey, 2003).
Established manual grain-size sampling methods, such as grid- or line-based pebble counts, are labour-intensive and time-consuming, physically intrusive and subject to operator sampling bias, which may result in the data under- or over-representing the relative frequency of different grain-size fractions within a given sample (Reference Bunte and AbtBunte and Abt, 2001; Reference Graham, Rollet, Piégay and RiceGraham and others, 2010). Such methods are also limited to patch-scale observation, defined here as an area of ground measuring ∼1 m2. While the spatial distribution of sampling campaigns can be optimized to ensure that these data sufficiently resolve the sedimentological complexity that exists within a given site, crucial sampling locations and their associated sedimentological characteristics may be omitted, often unintentionally, as no knowledge of variability is held, or assumptions about variability have been made a priori (Reference Graham, Reid and RiceGraham and others, 2005a).
Recent methodological advances have sought to improve the spatial coverage and representativity of surface sedimentological datasets. These advances have focused on the development of non-invasive, semi-automated approaches for obtaining grain-size distribution data from ground-based or low-altitude aerial photography using grain outline detection algorithms or textural information to retrieve grain-size characteristics from optical imagery (e.g. Reference Butler, Lane and ChandlerButler and others, 2001a,Reference Butler, Lane and Chandlerb; Reference Carbonneau, Lane and BergeronCarbonneau and others, 2004, Reference Carbonneau, Bergeron and Lane2005; Reference Graham, Reid and RiceGraham and others, 2005a,Reference Graham, Rice and Reidb; Reference BuscombeBuscombe, 2008; Reference Buscombe and MasselinkBuscombe and Masselink, 2009; Reference Dugdale, Carbonneau and CampbellDugdale and others, 2010; Reference Chang and ChungChang and Chung, 2012; Reference Detert, Weitbrecht and MuñozDetert and Weitbrecht, 2012; Reference Black, Carbonneau, Church and WarburtonBlack and others, 2014; Reference Tamminga, Eaton and HugenholtzTamminga and others, 2015). Additional advances include the application of close-range photogrammetry (e.g. Reference Butler, Lane and ChandlerButler and others, 1998) or terrestrial laser scanning (TLS) for recovering bulk morphological and sedimentological characteristics of surface sediments from fine-resolution topographic datasets (e.g. Reference Heritage and MilanHeritage and Milan, 2009; Reference Hodge, Brasington and RichardsHodge and others, 2009a). Crucially, these advances and their applications have tended towards a specific focus on exposed fluvial gravel surfaces (e.g. Reference Carbonneau, Lane and BergeronCarbonneau and others, 2004; Reference Graham, Rice and ReidGraham and others, 2005b; Reference Brasington, Vericat and RychkovBrasington and others, 2012; Reference Chang and ChungChang and Chung, 2012; Reference Bertin, Friedrich, Delmas, Chan and Gimel’farbBertin and others, 2014), which typically display a greater degree of particle sorting and increased clast roundness relative to comparatively unsorted and angular glacially derived sediments. Applications of photogrammetry to glacial environments have included digital surface modelling (e.g. Reference Baltsavias, Favey, Bauder, Bösch and PaterakiBaltsavias and others, 2001) and change detection (e.g. Reference Pitkänen and KajuuttiPitkänen and Kajuutii, 2004; Reference Keutterling and ThomasKeutterling and Thomas, 2006; Reference Eiken and SundEiken and Sund, 2012; Reference Whitehead, Moorman and WainsteinWhitehead and others, 2014), and the quantification of glacier surface roughness (e.g. Reference Kääb, Pellikka and ReesKääb, 2010; Irvine-Reference Irvine-Fynn, Sanz-Ablanedo, Rutter, Smith and ChandlerFynn and others, 2014; Reference Rippin, Pomfret and KingRippin and others, 2015). However, applications for the sedimentological characterization of glacial sediments, which may be highly complex, are currently lacking.
In this study, we appraise the utility of fine-resolution topographic models derived from ground- and unmanned aerial vehicle (UAV)-based Structure-from-Motion (SfM) with multi-view stereo photogrammetry for the extraction of grain-size information across a blue-ice moraine complex in the Heritage Range, Antarctica. We validate our approach through comparison with equivalent patch-scale datasets acquired using manual dry-sieving, photo-sieving and TLS. This research represents the first application of these semi-automated techniques, using only optical photographs and ground control as input, for measuring sedimentological characteristics of glacial sediments. Specifically, the research investigates three questions: (1) can SfM photogrammetry be used to quantify glacial sediment surface sedimentology? (2) how do these data compare with results obtained through established methods, namely manual dry-sieving and TLS? and (3) is it possible to upscale observation from the patch scale to the site scale (0.3 km2) through the deployment of a UAV?
Study Site
The study site is an ice-marginal embayment in the Patriot Hills, West Antarctica. The Patriot Hills are located at the mouth of Horseshoe Valley, a 45 km long, 25 km wide and 1500 m deep glacial trough, and, along with neighbouring Independence and Marble Hills, comprise the southern extent of the Heritage Range (Fig. 1). The geology of the range comprises marble and limestone conglomerates that are overlain by a succession of greywackes and conglomerates, shales and argillites of the Hyde Glacier and Drake Icefall Formations, and which are successively overlain by quartzites of the Minaret Formation (Reference Fogwill, Hein, Bentley and SugdenFogwill and others, 2012).

Fig. 1. Patriot Hills, southern Heritage Range, West Antarctica. (a) QuickBird satellite image of the ice-marginal blue-ice moraine embayment. Green = TLS positions for embayment scanning; yellow = 1 m2 patches surveyed using TLS and SfM; red = 1 m2 patches surveyed using SfM only. (b) Oblique perspective photograph of the central moraine ridges, with large limestone boulder erratics clearly visible. (c) Surface sediment on the western portion of the site.
The embayment hosts a suite of blue-ice moraines, forming a succession of east-west-oriented ridges that lie largely parallel to the present-day ice margin. These ridges extend upslope and trace the foot of the escarpment for >4 km, before curving to the northwest as a result of local ice flow patterns (Fig. 1). Beginning at the ice margin, the upslope sequence of key geomorphological features comprises ice-marginal hummocky moraine and thermokarst melt ponds, a series of moraine ridges and troughs, some of which are undergoing solifluction, and rockfall deposits on upper slopes (Fig. 1; Reference Vieira, Hinata, da Rosa, Zilberstein and SimoesVieira and others, 2012). The moraine ridges are visibly different in terms of relative relief, sedimentology and surface weathering. While the topography of the escarpment ranges from an elevation of ∼1000 to ∼1200 m a.s.l., the active blue-ice moraines are confined to the lowest 60–70 m of this range. The embayment is contained to the east and west by bedrock spurs that are covered by a till drape, overlain by large sandstone boulder erratics that can be traced over the blue-ice moraines.
Methods and Data Products
Sedimentological data can be extracted (1) from patch-scale locations using optical imagery combined with ‘photo-sieving’ methods or (2) from relationships derived from relating the sediment median grain size (D 50) to topographic statistics (e.g. Reference Hodge, Brasington and RichardsHodge and others, 2009a). Photo-sieving permits the automatic extraction of grain-size information from optical imagery of unconsolidated sediment (Reference AdamsAdams, 1979; Reference Ibbeken and SchleyerIbbeken and Schleyer, 1986; Fig. 2). Orthorectification of SfM input imagery permits its use as the sole input to photo-sieving. The aims of photo-sieving were: (1) to appraise the performance of the technique at estimating the grain-size distribution of moraine surface sediment at the patch scale; (2) to recover grain-size distribution data for an additional nine patches where control data were not collected; and (3) to extract the D 50 grain-size fraction for each patch from photo-sieving results. Median grain-size data were then combined with a measure of patch-scale topographic roughness to derive a relationship, which, through application to the site-scale UAV-SfM data, can facilitate upscaling from patch- to site-scale sedimentological characterization. In the absence of independent control datasets at both scales, the TLS data were used as the reference for registration of the equivalent SfM datasets and served as a benchmark against which to evaluate the performance of SfM photogrammetry.
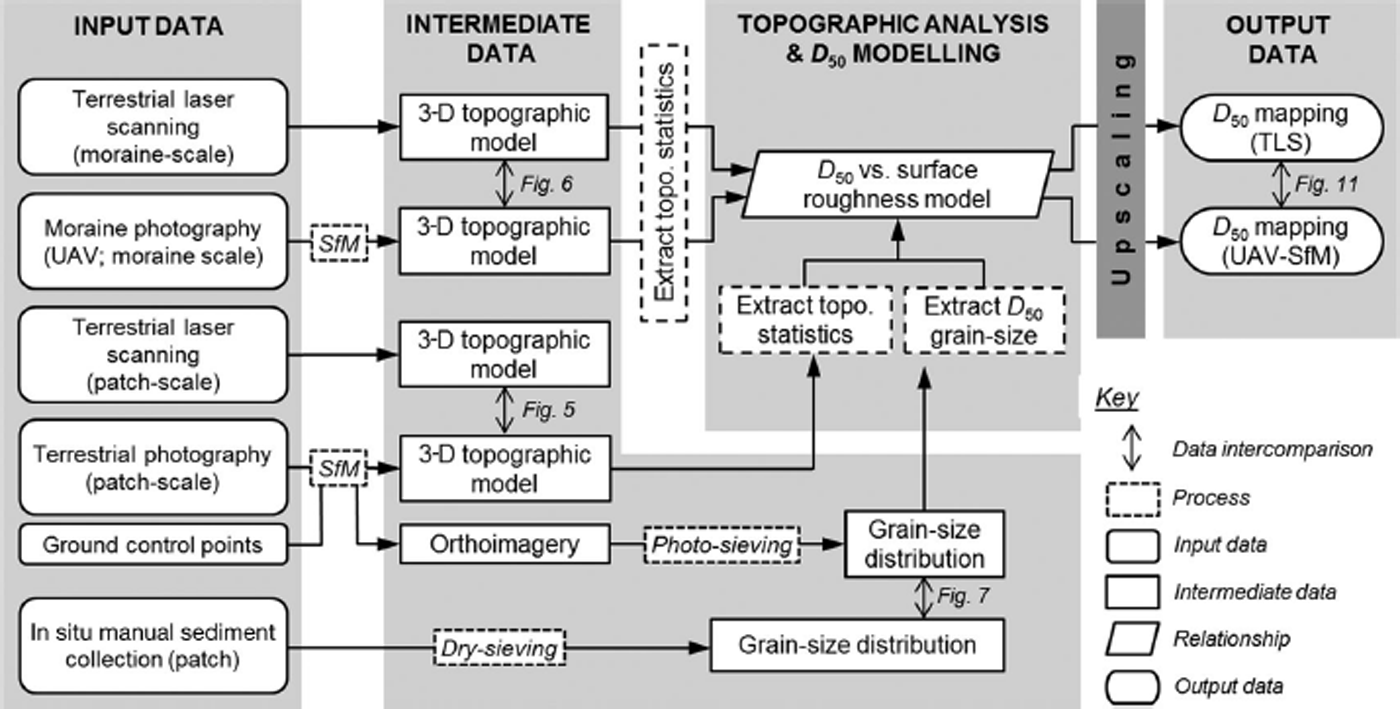
Fig. 2. Modelling workflow for upscaling from patch- to site-scale median grain-size mapping.
Photo-sieving validation comprised the collection of all surface sediment from three 1 m2 patches on the moraine (patches 1–3; Fig. 1) to ∼10 cm depth. This depth specification ensured that clasts which may have been partly, or mostly, buried, but which would still be visible in the SfM orthoimagery and would therefore contribute to the photo-sieving-derived grain-size distribution curve, were collected. These samples represent sediment at the ice margin (patch 1), mid-moraine sediment (patch 2) and sediment at the rear of the embayment (patch 3). These patches were surveyed using TLS and ground-based SfM photogrammetry prior to sediment collection.
Manual grain-size classification
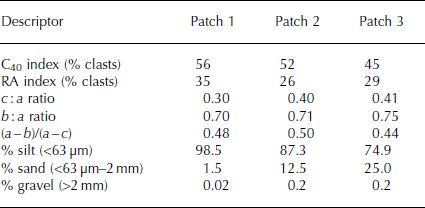
Patch samples were dried and dry-sieved in a laboratory to determine the mass fraction of clasts ranging in size from −6.0ϕ (91 mm) to 4.0ϕ (63 μm). A Malvern Mastersizer 2000 particle size analyser was used to determine the grain-size distribution of the finest fractions (<63 μm) through laser diffraction. The lengths of a-, b- and c-axes were recorded for a representative sample of 50 clasts from the very coarse (>32 mm), coarse (16–32 mm) and medium gravel (8–16 mm) fractions for each sample. Clast roundness was recorded using a modified Reference PowersPowers (1953) chart. Clast shape was analysed by plotting the RA index (% angular and very angular clasts) against the C40 index (% clasts with a c/a axis ratio of ≤0.4) after the method proposed by Reference Benn and BallatyneBenn and Ballatyne (1993) and modified from Reference Sneed and FolkSneed and Folk (1958). Key sedimentological characteristics for the three patch samples are shown in Table 1.
Table 1. Sedimentological descriptors of moraine surface material collected from patches 1–3. Values represent the arithmetic mean of data collected for clasts in the range 8–64 mm, with the exception of % silt, sand and gravel, which reflect composition of a total sediment sample (patches 1–3 = 9.4 kg, 7.0 kg and 6.7 kg, respectively)
Terrestrial laser scanning
Patch-scale terrestrial laser scanning
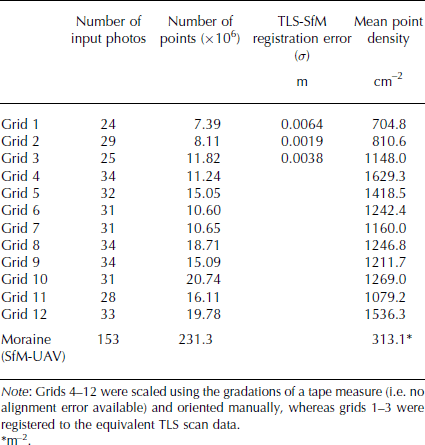
Patch- and site-scale TLS was undertaken using a Riegl LMS-Z620 time-of-flight laser scanner, set to acquire 11 000 points s−1 in the near-infrared band (21 400 Hz) at a horizontal and vertical scanning resolution of 0.043°. The scanner was deployed ∼4.5 m from the centre of each patch, producing a laser-beam spot size of 14.5–14.8 mm and a point spacing of 0.5–0.8 mm across each patch. TLS scan data were acquired from the four cardinal directions at each patch. Average point densities for individual patch scans ranged from 26.5 to 40.4 points cm−2 (Table 2) at a manufacturer-stated nominal scanning precision of 5 mm and accuracy of 10 mm (Riegl Laser Measurement Systems, 2010).
Table 2. Terrestrial laser scanning statistics

For patches 1–3, ground-control points (GCPs) comprised four 7 cm diameter and five 4 cm diameter circular retroreflective targets, positioned evenly and alternately around the edge of each patch (Fig. 3). One of the smaller targets was placed in the centre of each patch to form a centroid, and all targets were visible from multiple scan positions. Scan data were aligned to a single oriented scan position for each patch using RiSCAN PRO software (version 1.5.9). A two-step method of data transformation was employed: (1) common GCPs were used as input to a coarse, rigid-body linear transformation to shift and rotate the data, without any rescaling or surface deformation; (2) residual alignment errors were then minimized through the creation of overlapping surface patches in each point cloud on areas of relatively planar topography (e.g. boulder faces) and a linear, iterative, least-squares minimization solution applied to improve the transformation and reduce sources of alignment error (Table 2). TLS data were merged and clipped to create a single point cloud for comparison with the equivalent SfM digital elevation models (DEMs). Additional documented sources of error in TLS data are summarized by Reference Hodge, Brasington and RichardsHodge and others (2009a) and include those associated with issues of data precision or repeatability, surface reflectivity and target feature geometry, whereby the interaction of the laser footprint with clast edges causes mixed pixel and angular displacement errors.

Fig. 3. From photograph to SfM-derived orthoimagery. Top: Example dense SfM point cloud for patch 1 (2.5 m2). Reconstructed camera positions are shown in blue. Large (7 cm diameter) ground control points (GCP) are also highlighted. Red outline shows 1 m2 area of patch 1 orthoimagery shown in bottom panel. Bottom: Photo-rendered orthoimagery extracted from the SfM models and used as the sole input to photo-sieving.
Site-scale terrestrial laser scanning
TLS scan data were acquired from three positions across the moraine (Fig. 1a) at nominal vertical and horizontal scanning increments of 0.031°, equivalent to an average point spacing of 5 cm at a range of 100 m. A combination of retroreflective, pole-mounted and ground-based GCPs were distributed across the moraine and used for coarse scan alignment. One TLS scan (TLS_2; Fig. 1) was used as a static reference to which the two subsequent sets of scan data (TLS_1, TLS_3) were registered. Surface plane-based point-cloud alignment was undertaken using common GCPs and unchanged features.
Structure-from-Motion photogrammetry
Patch-scale SfM surveying
SfM methods use a series of input images with overlapping view perspectives to simultaneously reconstruct three-dimensional (3-D) camera pose and sparse scene geometry using an iterative bundle-adjustment procedure (Reference Snavely, Seitz and SzeliskiSnavely and others, 2008; Reference James and RobsonJames and Robson, 2012; Reference Westoby, Brasington, Glasser, Hambrey and ReynoldsWestoby and others, 2012). Estimated camera poses and image clustering and multi-view stereo methods are then used to increase the density of the sparse point cloud by up to two orders of magnitude (e.g. Reference Furukawa and PonceFurukawa and Ponce, 2007; Reference Furukawa, Curless, Seitz and SzeliskiFurukawa and others 2010).
Twelve patches, including the three surveyed by TLS (patches 1–3), were photographed from ground-based oblique and near-nadir perspectives using a consumer-grade 16-megapixel, Nikon D7000 digital camera set to a fixed focal length of 18 mm and automatic exposure settings enabled. The number of photographs used for 3-D reconstruction of patch topography varied from 24 to 34, with an average of 30. Photographs were acquired using a highly convergent configuration in order to avoid systematic reconstruction errors associated with the use of non-convergent image networks (Fig. 3; Reference James and RobsonJames and Robson, 2014). Sparse and dense 3-D point clouds of the patch surface geometry were generated in Agisoft PhotoScan Pro (Reference AgisoftAgisoft, 2014).
For patches 1–3, GCP centroids were identified in the input images and their locations projected onto a dense surface mesh to obtain 3-D coordinates in the model object space. GCP xyz locations were taken from the equivalent TLS model, and the initial camera alignment was optimized by re-executing the bundle adjustment algorithm with GCP locations taken into account in order to remove any nonlinear model deformations arising from poorly estimated camera poses. The SfM models were reprocessed using the optimized camera configurations to produce final, dense SfM point clouds (Fig. 2). Patch-scale SfM models were clipped to the same 1 m2 area as the equivalent TLS scans. Patches 4–12 were scaled using gradations visible on a tape measure in the scene and manually rotated so that the xy surface plane was horizontal, thereby guaranteeing that the SfM-derived orthophotograph of each plot is an accurate reflection of the horizontal surface geometry and that issues of image foreshortening would not affect the accuracy of subsequent photo-sieving. To establish whether this (necessarily) simplified method of data transformation would affect the quality and accuracy of the point-cloud data, we compared the surface geometry of two SfM-derived point clouds for patch 1 using an Iterative Closest Point (ICP) algorithm: one which had undergone the full optimization and georeferencing workflow, employing a network of GCPs; and another which was subject to no form of camera optimization or georeferencing. Comparison of these models revealed a mean difference of 1.7 mm across the model area, and supports our method of scaling patches 4–12 using an object of known length in the absence of a full GCP network (cf. patches 1–3). We deem this difference to have an insignificant effect on the subsequent extraction of metric data, specifically grain-size information from the orthophotographs, and, later in our workflow, the standard deviation of local surface elevations.
Patch-scale SfM reconstructions yielded, on average, a 26-fold increase in the number of 3-D points that describe the surface topography compared to the equivalent TLS data (Tables 2 and 3). The performance of the SfM reconstruction benefits from the highly textured moraine surface, which comprises a range of clast shapes, sizes, lithologies and microscale shadowing effects produced by facets on individual clasts; all of which add contrast to the scene and aid keypoint recovery. Our method of photograph acquisition (Fig. 3) ensured that the surface topography was captured completely. The resulting SfM models therefore do not suffer from data gaps resulting from the line-of-sight losses which affect TLS data coverage.
Table 3. Structure-from-Motion processing statistics
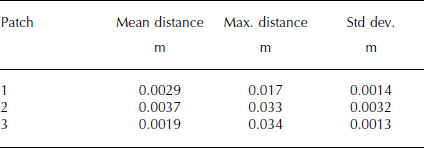
In the absence of an independent measure of SfM and TLS data quality, we employ cloud-to-cloud differencing, whereby the distance between a given 3-D point in one cloud and the closest equivalent 3-D point in a second cloud is quantified, to compare the reconstruction accuracy of the SfM patch surface topography to the equivalent TLS scan data. Cloud-to-cloud differencing revealed sub-millimetre mean differences between the TLS and SfM datasets (Fig. 4; Table 4). The largest cloud-to-cloud deviations typically correspond with regions of decreased TLS point density in the lee of larger clasts which were not resolved in as much detail as the equivalent SfM data, and might also be attributed to mixed-pixel errors in the TLS data, caused by the laser footprint splitting as it intersects clast edges (Reference Hodge, Brasington and RichardsHodge and others, 2009a).

Fig. 4. Results of cloud-to-cloud differencing of the TLS and ground-based SfM data for patch 1. (a) SfM orthophotograph; (b) cloud-to-cloud difference image. The largest differences generally correspond with regions of decreased TLS point density such as the lee of larger cobbles which were reconstructed in higher density by the SfM model.
Table 4. Patch-scale cloud-to-cloud (TLS-SfM) differencing statistics
Site-scale SfM surveying
The embayment was photographed from a fixed-wing, sub-5 kg UAV using a 10-megapixel Panasonic Lumix DMC-LX5 compact digital camera, with a fixed focal length of 8 mm and with automatic exposure settings enabled. Photograph acquisition at original resolution was undertaken at an average flying height of 120 m, producing an approximate relative image scaling of 7 cm2 per pixel. However, due to the static, downward-facing perspective of the UAV camera, photographs were not collected in a convergent configuration. Input photographs were processed in the same manner as the patch-scale photography to create a single dense point cloud. The dense UAV-SfM data (Fig. 5a) were aligned with the site-scale TLS datasets using iterative closest point adjustment and surface plane matching across unchanged bedrock features (Table 3).
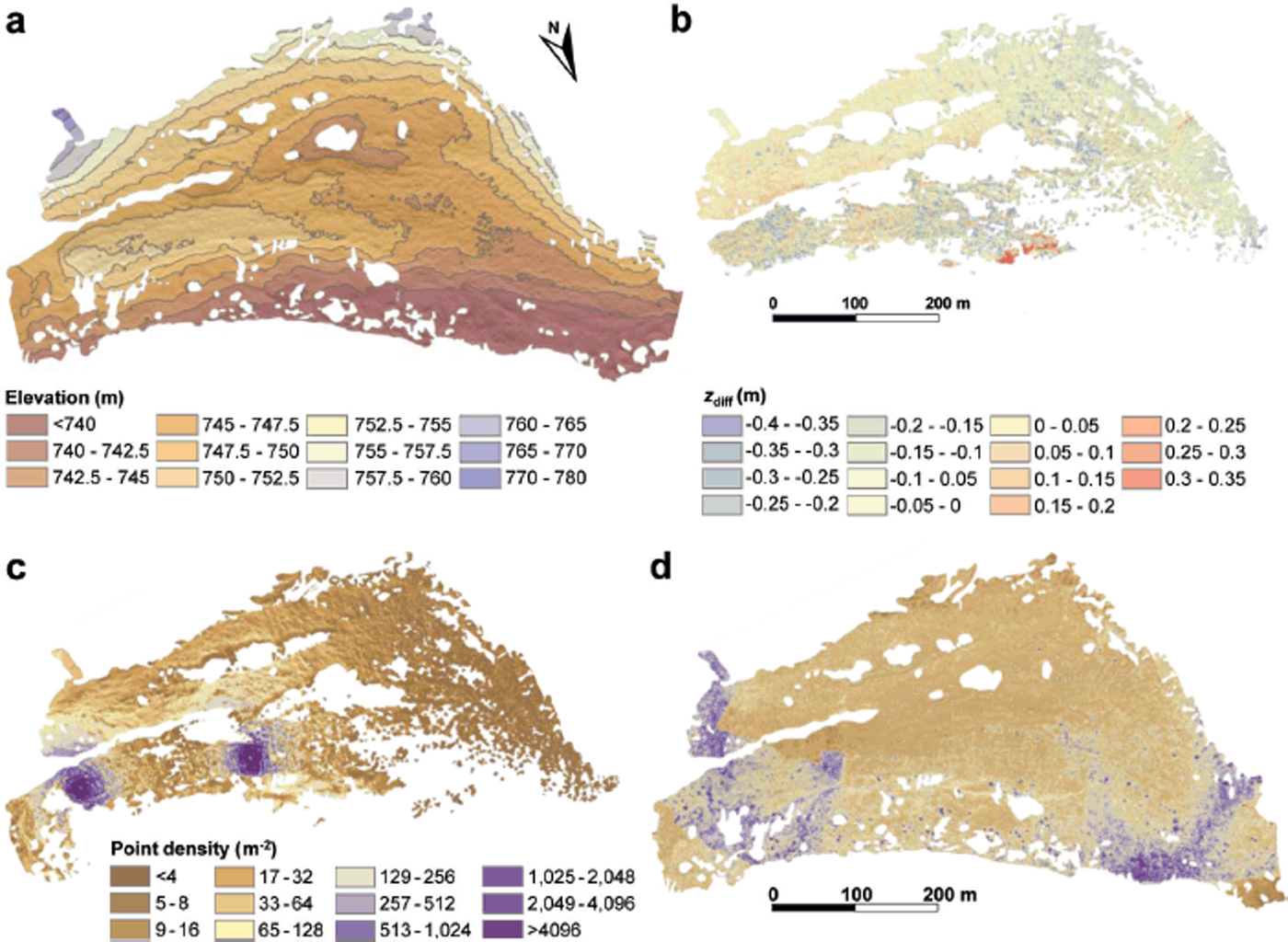
Fig. 5. (a). A hillshaded, SfM-derived DEM of the study site, produced using imagery acquired from a fixed-wing UAV, and georegistered using site-scale terrestrial laser scanning data. (b) A DEM of difference, creating by rasterizing and subtracting the moraine-scale UAV-SfM DEM from the TLS DEM. The mean vertical error (z diff) is −0.054 m (σ = 0.16 m). (c, d) Point density data (m−2) for (c) TLS, and (d) SfM-UAV moraine surface topography.
Comparison of site-scale TLS and SfM data
Site-scale TLS data comprise data merged from three separate scan positions (Fig. 1a) and exhibiting two zones of increased density adjacent to the scanner positions (Fig. 5c). To capture TLS data of comparable density to the SfM data would require data to be acquired from several scan positions, requiring manual system remobilization or the use of a mobile laser scanner (e.g. Reference James and QuintonJames and Quinton, 2013; Reference Williams, Brasington, Vericat and HicksWilliams and others, 2014), neither of which are currently viable options in such a challenging environment. The point density of the UAV-SfM model is more uniform and generally exceeds that of the TLS data (Fig. 5d). Areas of increased point density across the UAV-SfM model are generally the result of photograph density; areas at the extreme east and west of the site, where UAV banking took place, were photographed at the highest densities. To assess the relative accuracy of the UAV-SfM data, a DEM of difference was created by gridding both datasets at 1 m2 resolution using the per-cell mean elevation, and subtracting the UAV-SfM topography from the TLS data. Differencing produced a mean vertical error of −0.054 ± 0.16 m for the UAV-SfM data (Fig. 5b).
Photo-sieving
Photo-sieving methods employ a combination of edge-detection, greyscale-thresholding and image segmentation algorithms to identify and measure the a- and b-axes of individual clasts (e.g. Reference Graham, Reid and RiceGraham and others, 2005; Reference Detert, Weitbrecht, Fukuoka, Nakagawa, Sumi and ZhangDetert and Weitbrecht, 2013), or use statistical functions that describe the textural signature of the input image and use these data to estimate grain-size characteristics and distribution (e.g. Reference Dugdale, Carbonneau and CampbellDugdale and others, 2010; Reference BuscombeBuscombe, 2013). The minimum observable grain size, which is determined by the resolution of the input imagery, will truncate the lower end of the distribution and require the user to estimate the contribution of the finest, unobservable sediment fractions to the overall distribution, either manually, or through the use of a statistical function (e.g. Reference Detert, Weitbrecht, Fukuoka, Nakagawa, Sumi and ZhangDetert and Weitbrecht, 2013).
Gravelometric analysis of moraine sediment was undertaken using the MATLAB®-based object detection software BASEGRAIN (Reference Detert, Weitbrecht and MuñozDetert and Weitbrecht, 2012, Reference Detert, Weitbrecht, Fukuoka, Nakagawa, Sumi and Zhang2013). Following camera alignment optimization, an orthographically correct image (1 pixel = 0.5 mm ground spacing) of each patch was exported from PhotoScan and used as the sole input to photo-sieving. BASEGRAIN requires a plan-view (ideally orthographic) photograph with a known scaling as input, and employs a multi-step procedure to identify and measure grain geometry to construct a quasi-grain-size distribution curve. In the order that they are encountered in the processing workflow, the software employs: (1) greyscale thresholding, (2) bottom-hat filtering and (3) edge detection methods to identify grain interstices; and (4) watershed separation to identify individual grains (Fig. 6). A final step is required to fit a- and b-axes to individual grains, filter identified grains using user-specific upper and lower median grain diameter and calculate ellipsoidal grain area, perimeter, a/b axis ratio, the local coordinate of the grain centre, and the grain orientation in the horizontal plane (Reference Detert, Weitbrecht and MuñozDetert and Weitbrecht, 2012). The minimum identifiable grain diameter was specified as 8 mm, which equals an image distance of 16 pixels. The outlines of grains with b-axis <16 pixels were difficult to delineate and were excluded from the automated classification. No upper limit was specified. The grain-size distribution of clasts possessing an intermediate diameter <8mm is approximated using a Fuller curve approximation (Reference Fuller and ThompsonFuller and Thompson, 1907; Reference Fehr and LarsenFehr, 1986) derived from the estimated packing density of concrete aggregates, and is calculated as

Fig. 6. Selected BASEGRAIN processing steps. (a) Input photo-rendered orthoimage of dense SfM surface model. (b) Interstice detection by double greyscale thresholding. (c) Morphological bottom-hat transform. (d) Final particle outlines (red) and a- and b-axis assignment (blue).
where P is the percentage of sample finer than a given fraction, d is the size fraction under consideration, D is the maximum clast size (mm) in the sample, and n is a user-defined dimensionless exponent, which in this study was manually adjusted to ensure overlap between the largest grain-size fraction represented by the Fuller curve and the finest measured clast fractions. The Fuller curve-derived distribution is combined with the photo-sieved data through a least-squares fit in overlapping regions (Reference Detert, Weitbrecht and MuñozDetert and Weitbrecht, 2012).
Manual post-processing is used to merge, split or remove incorrectly classified grains. Output data comprise a grain-size distribution curve, derived either from digital line-sampling of the final classified image, whereby a digital grid with a user-specified spacing is overlain on the classified grain image and grains which intersect these gridlines are used to construct a grain-size distribution (Reference Fehr and LarsenFehr, 1986), or directly from the cumulative distribution of individual grain areas. While the results from these two methods generally provide good agreement (e.g. Reference Detert, Weitbrecht and MuñozDetert and Weitbrecht, 2012), the latter approach was used and is directly comparable with the results from dry-sieving. SfM orthoimagery was cropped to a 1 m2 area to ensure correspondence with the equivalent surface area from which moraine sediment was collected in the field. Comparison of the orthophotograph pixel area to the surface pixel area of the largest identified grain for each patch produced a mean ratio of 147 : 1, which is consistent with ratios recommended by Reference Diplas and FrippDiplas and Fripp (1992) and Reference Graham, Rollet, Piégay and RiceGraham and others (2010), who found percentile errors of <10% with a ratio of between 100 : 1 and 200 : 1.
Upscaling from patch- to site-scale sedimentological characterization
In order to characterize the surface sedimentology at the site scale, we employ a method for extracting the median grain size of surface sediments directly from high-resolution topographic data (Reference Brasington, Vericat and RychkovBrasington and others, 2012; Reference Rychkov, Brasington and VericatRychkov and others, 2012; Reference Smith and VericatSmith and Vericat, 2015). The method involves the derivation of a relationship between topographic statistics, specifically the standard deviation of local 3-D point elevations, and observed median grain size (Fig. 7). It is computationally efficient to implement for large 3-D topographic datasets, and overcomes issues of incomplete or unrepresentative characterization of surface sediments which might otherwise be associated with manual sediment sampling.
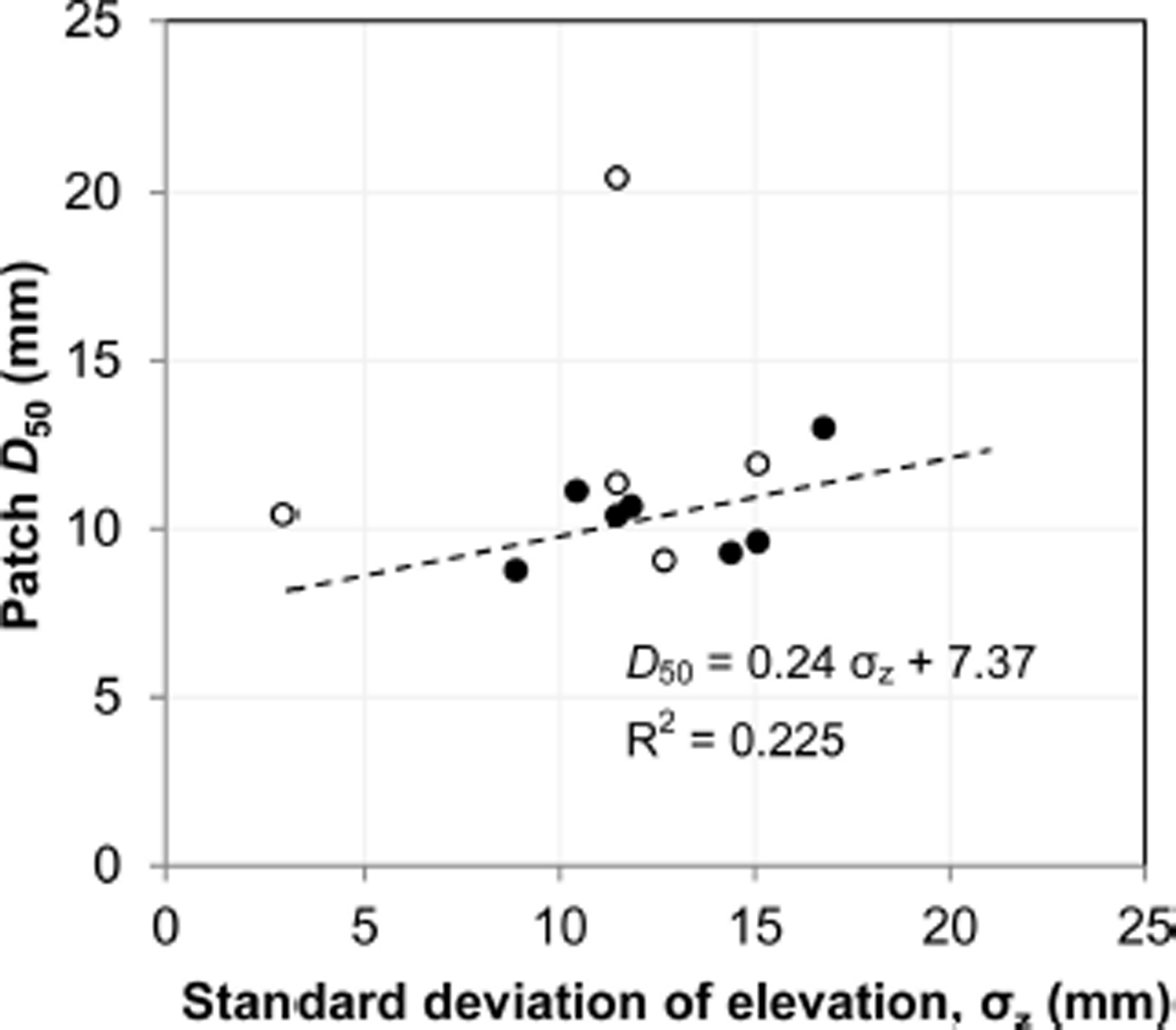
Fig. 7. Relationship between median grain size (D 50), as derived from digital photo-sieving of patch-scale SfM orthophotographs, and the detrended standard deviation of patch-scale SfM surface elevations. Data used to derive the relationship are shown as solid data points, while open data points were retained as check data to assess the accuracy of an upscaled, site-scale map of D 50 produced by applying the above relationship to the UAV-SfM data.
Median particle size was extracted from the BASEGRAIN data for all patches and plotted against the locally detrended standard deviation of surface elevation, as extracted from the SfM data using the Topographic Point Cloud Analysis Toolkit (ToPCAT; Reference Rychkov, Brasington and VericatRychkov and others, 2012) to give
where D 50 is the median particle size andz is the detrended standard deviation of local surface elevation. This relationship differs from the original of Reference Brasington, Vericat and RychkovBrasington and others (2012) given the derivation of their model from TLS-derived surface models of fluvial and coastal sediments, which are associated with characteristic grain shapes and depositional style, while we utilize SfM-derived surface models of glacial sediment. To demonstrate the difference between patch-scale TLS- and SfM-derived topographic statistics, we compared σ z values extracted from equivalent TLS and SfM models for patches 1–3, which revealed that TLS overestimated σ z by 13.8, 4.5 and 0.1 mm for patches 1–3 respectively relative to the SfM data.
Upscaling from patch- to site-scale characterization of median grain size is achieved through the subsequent application of this relationship to the UAV-SfM data. BASEGRAIN-derived estimates of sample D 50 were retained as check data for five patches (5, 7, 8, 10 and 12) that encompass the full variety of grain-size distributions observed across the moraine.
Results
Photo-sieving
Grain-size distribution curves derived from photo-sieving using the SfM patch orthomosaics are displayed in Figure 8. BASEGRAIN-derived grain-size distribution data for patches 1–3 and displayed by phi class (φ) are compared to the equivalent data derived from dry-sieving in Figure 8a. Deviations from the observed dry weight data are evident for each patch; median and maximum deviations are 0.3%, 0.25% and −1%, and 5%, 5.03% and 6.3% for patches 1–3, respectively. However, these deviations exhibit little systematicity, such that under- or overestimations are not concentrated in a particular region of the distribution. Grain-size curve data (Fig. 8b) are clustered according to their location across the moraine, such that patches 1, 4 and 8 represent ice-marginal deposits, patches 2, 5 and 9 are located on, or immediately adjacent to, a major moraine crest, while patches 3 and 7, and 6, 10 and 11 are positioned on subdued deposits to the rear of the moraine embayment, and in a central area of relatively subdued topography, respectively. The outlier in this region is patch 12, which is also located on a moraine crest and contains a higher proportion of coarse material than the other patches. Grain-size curves for ice-marginal deposits exhibit a strong dominance of fine material which appears to decrease with increasing distance from the ice margin and is perhaps attributable to increased sorting and burial, or winnowing, of the fine sediment fraction during moraine development. This area is one of generally gentle surface topography sloping towards the ice margin, interspersed with thermokarst melt ponds.
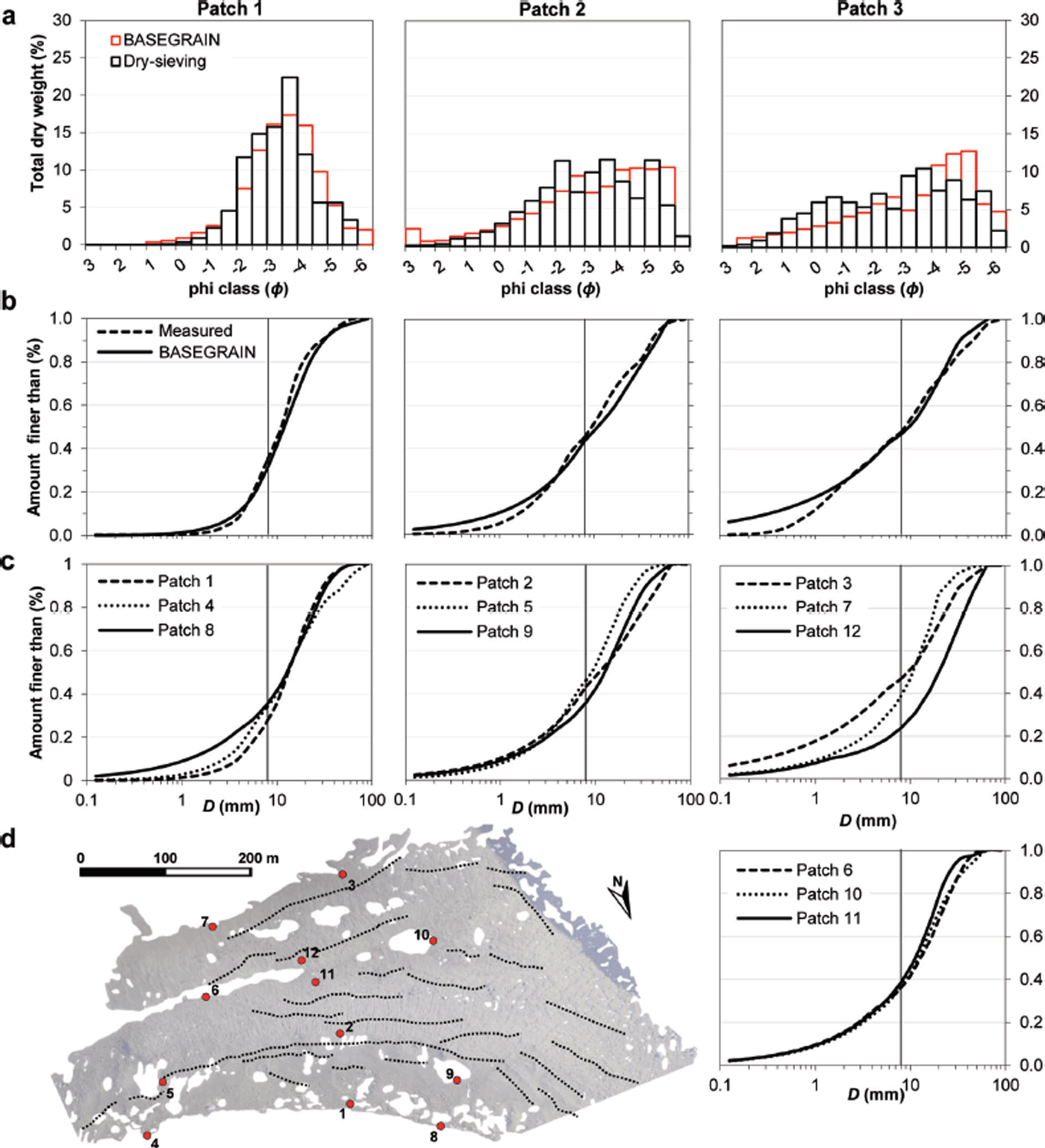
Fig. 8. Patch-scale grain-size distribution data. (a) Comparison of grain-size frequency distribution by phi class (a-axis), derived from drysieving and photo-sieving. (b) Cumulative grain-size distribution for the control patches (1–3), derived from dry-sieving and photo-sieving. Vertical line indicates 8 mm cut-off for grain detection in BASEGRAIN; the relative proportion of clasts <8 mm was estimated using a Fuller curve extension to the observed distribution. (c) Photo-sieved grain-size distribution data for patches 4–12, for which no control data were available. (d) Site map showing patch locations (red dots) and the location of moraine crests (dashes).
Following the manual splitting, merging or removal of misclassified grains, the number of classified grains m−2 ranged from 425 grains m−2 for patch 2 (compared to an observed count of 736 grains) to 3228 grains m−2 for patch 10, with a mean of 1741 grains m−2. Classified grain areas represented 75%, 85% and 74% of the total image area for patches 1, 2 and 3 respectively, and between 72% and 90% for patches 4–12 (mean for all patches 76%). The remaining void area represents grains with a-axis lengths of <8 or >90 mm, grains with boundaries that intersect the image boundary, and cast shadows. It is also observed that, as the proportion of small grains in the input imagery increases, the number of recovered grain outlines also increases. Grain-size distribution curves generally mirror the control data for grain-size fractions greater than the automated classification threshold of 8 mm, with minor over- or underestimations along this distribution (Fig. 8b; Table 5).
Table 5. Grain-size percentile diameters (a-axis; mm), measured using dry-sieving and estimated using BASEGRAIN, and percentile errors. Errors in italics reflect BASEGRAIN fractions that fall below the minimum detectable grain-size diameter of 8 mm
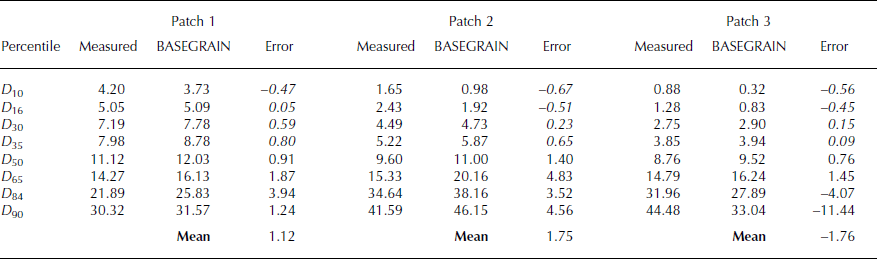
Percentile errors are shown in Table 5. Photo-sieving overestimates the relative contribution of fines, and generally underestimates the contribution of larger grains to the overall distribution for all control patches (Fig. 8b). Errors increase with grain-size fraction, with deviations of up to −11.44 mm (D 90, patch 3) from the measured data observed for the larger percentiles (Table 5). Sub-millimetre errors are observed in the area of the curve estimated by the Fuller extension (i.e. <8 mm, percentiles D 10–D 35). Mean errors for the entire distribution are 1.12 mm, 1.75 mm and −1.76 mm for patches 1–3, respectively.
Site-scale median grain-size mapping
Equation (2), which describes median grain size as a function of the detrended standard deviation of local surface elevations, was applied to the dense SfM data to produce a spatially continuous map of D 50 at the moraine scale (Fig. 9a). Check data, comprising D 50 estimates for five patches which were not used to derive Eqn (2), were compared with the mean D 50, which was calculated within a 3m2 window around the centroid of each patch. This window size was deemed to be of sufficient size to contain the area of each ground patch. We also assume that the surface sedimentology in this window does not significantly deviate from that observed for each patch, which is a sound assumption based on field observations and visual analysis of field photography. Comparison of these check data with the site-scale D 50 mapping reveals errors ranging from +0.83 to −10.85 mm (mean −2.90 mm).

Fig. 9. (a) Moraine-scale surface sediment D 50 mapping derived from UAV-SfM photogrammetry. Red crosses show patch locations. The lowest D 50 values are found closest to the ice-margin across areas of relatively subdued topography. In contrast, larger median grain sizes are found across the central moraine. The largest values correspond with the location of individual boulder erratics, or boulder clusters. The large (20–40 mm) values of D 50 at the eastern margin (figure left) of the site highlight a bedrock outcrop, while those at the southern margin (figure top) are rockfall deposits. (b) Site-scale median grain-size mapping, thresholded to highlight cells that represent D 50 > 32 mm (red dots) and which can be used to isolate individual boulders or clusters of boulders. Inset panel shows comparison of thresholded cells with the location of large boulders visible in the equivalent SfM orthophoto.
The majority of the site possesses a median grain size of <15 mm. Within this fraction, areas with the lowest D 50 (<11 mm) are largely confined to topographically subdued areas, including those adjacent to the ice margin and intermoraine trough towards the rear of the basin (Fig. 9), while larger D 50 values (>15 mm) characterize areas at the foot of the surrounding slopes. This classification corresponds with field observations, whereby material located at the ice margin and to the rear of the embayment are likely to be preferentially subjected to in situ weathering. In contrast, coarser material on the moraine flanks and crests was observed to be subject to reworking and active slope processes, causing the regular ‘resetting’ of sediment sorting and the preservation of a comparatively rough surface signature. The coarsest sediments are found on the proximal and distal faces of the larger moraines across the centre of the site, where active reworking by slope processes prevents in situ weathering and clast comminution.
Gridcells containing boulder-sized clasts are defined as possessing a D 50 value >32 mm (Fig. 9b). While the grain-size classification of a ‘boulder’ varies in definition (e.g.
64 mm (Reference Friedman and SandersFriedman and Sanders, 1978) or 512 mm (Reference Blott and PyeBlott and Pye, 2001)), we find that, for individual boulders smaller than the grid size of 1m2 in particular, this thresholded measure of D 50 is suitable for identifying gridcells containing boulder-sized clasts, and is verified through comparison with the UAV-SfM orthoimagery (Fig. 9b, inset). The fact that this limit is considerably smaller than the smallest definition of a ‘boulder’ is explained as the result of the remaining gridcell area being composed of much smaller grains, which decreases the standard deviation of surface elevations. Individual boulders and boulder ‘clusters’ are scattered across the moraines, with notable concentrations found in the centre of the site. Where individual boulders span the boundary of two or more cells, or possess a plan-view clast area greater than 1 m2 and could therefore be contained within multiple adjacent cells, the result is an overestimation of the clast footprint. While not addressed here, this may be overcome by increasing the ToPCAT cell size in order to increase the likelihood of individual large clasts being contained within a single cell and thereby minimizing, or altogether eliminating, any influence on the median grain size of the surrounding cells. Such adjustments would need to be carefully optimized to avoid the over-generalization of local surface topography, such that multiple local topographic variations are not contained within a given cell, in which case surface roughness, or standard deviation of elevation, will retain a topographic signal and therefore be unrepresentative of grain-size characteristics.
Discussion
The key outcome of this research is the finding that upscaling from patch- to site-scale sedimentological characterization of glacial moraines is possible through the combination of UAV-SfM photogrammetry and topographic characterization. This combination of techniques overcomes issues of incomplete spatial coverage typically associated with highly selective and labour-intensive manual field measurement, or the use of static TLS. The following subsections discuss the logistical merits and shortcomings of our methods, the suitability of photo-sieving and spatial upscaling for characterizing the surface sedimentology at the patch- and site scales, and the wider implications of the research for augmenting process-based glacial geomorphological investigation.
Methodological appraisal
Key objectives of this research included the appraisal of methods designed to reduce sedimentological surveying times relative to traditional, labour-intensive methods (Reference Bunte and AbtBunte and Abt, 2001). TLS data acquisition took ∼2 hours per patch, and required an additional 2 hours per patch to co-register the four individual scans, in addition to the time, effort and additional resources (e.g. power supply) required to transport, operate and maintain a terrestrial laser scanner for an extended period in a remote environment. In contrast, patch-scale SfM photography, using a consumer-grade digital camera, took ∼2 min per patch, while the generation of dense 3-D point clouds took ∼4 hours per patch.
For photo-sieving, user interaction largely amounted to manually redigitizing the outlines of misclassified grains, and took ∼30–45 min per 1 m2 patch. In contrast, in situ collection of sediment, dry-sieving, and laser diffraction to derive the control datasets took ∼3 hours per patch, not including the time required to transport the samples from the field site. Similarly, while the acquisition of the basin-scale TLS scans took ∼60 min per scan, in addition to subsequent post-processing required to align and co-register the individual scans, a single UAV sortie, lasting no more than 5 min, was all that was required to acquire the input photography for site-scale SfM reconstruction. We note, however, that additional ground control, provided here by the site-scale TLS scans, is required to transform the data from a local to an absolute coordinate system. Such control is more easily acquired using differential GPS to locate either natural features in the survey extent, or a network of placed targets (e.g. Reference Javernick, Brasington and CarusoJavernick and others, 2014; Reference Williams, Brasington, Vericat and HicksWilliams and others, 2014). Given the demonstrable accuracy of the SfM technique at reconstructing moraine surface topography (Fig. 4) and natural topography in a range of environments (e.g. Reference James and RobsonJames and Robson, 2012; Reference Westoby, Brasington, Glasser, Hambrey and ReynoldsWestoby and others, 2012; Reference Javernick, Brasington and CarusoJavernick and others, 2014; Reference Nouwakpo, James, Weltz, Huang, Chagas and LimaNouwakpo and others, 2014; Reference Stumpf, Malet, Allemand, Pierrot-Desilligny and SkupinskiStumpf and others, 2014; Reference Smith and VericatSmith and Vericat, 2015; Reference Tamminga, Eaton and HugenholtzTamminga and others, 2015), the significant gains in data acquisition and processing time in our findings advocate its use for the surface topographical and sedimentological characterization of glacial sediments.
Grain-size classification
While the general form of the grain-size distribution curves for fractions >2 mm exhibits little deviation from the control data, minor offsets in the calculated grain diameter are observed (Fig. 8; Table 5). These deviations are attributed to a range of effects including the presence of cast shadows (caused by a low solar azimuth angle) which serves to eliminate smaller, hidden grains from the final classification and causes an overestimation of the percentage of larger material (e.g. Reference Graham, Reid and RiceGraham and others, 2005a; Reference Buscombe, Rubin and WarrickBuscombe and others, 2010). This issue might be overcome in future studies through the use of a portable, static light source to significantly reduce, or altogether eliminate, clast shadowing. Other explanations, specifically for the software overestimating the percentage of the largest fractions, might include grain foreshortening, whereby grains, particularly those found in the interstices between larger grains, present their c-axis to the camera, resulting in underestimation of their true size (Reference Butler, Lane and ChandlerButler and others, 2001; Reference Carbonneau, Lane and BergeronCarbonneau and others, 2004; Reference Graham, Rollet, Piégay and RiceGraham and others, 2010). Such grain-structuring effects may operate selectively across different fractions of the grain-size distribution (Reference Graham, Rollet, Piégay and RiceGraham and others, 2010). For instance, selective reduction of the size of coarse grains (>8 mm) may explain the almost consistent under-estimation of these fractions. An additional consideration is the unintentional collection of buried (small) clasts during manual sampling. The inclusion of these additional clasts in the dry-sieving samples may have skewed the manually measured grain-size distribution for the control patches so that it overestimates the true proportion of finer material to the overall distribution and underestimates the relative contribution of larger clasts.
The ground resolution of the UAV photography, which is limited by the resolution of the on-board camera and flying height, rendered it unsuitable for identifying individual clasts (e.g. Reference Carbonneau, Bergeron and LaneCarbonneau and others, 2005), although the application of texture-based photo-sieving methods may make it capable of estimating the grain-size fraction of specific percentiles for such imagery (e.g. Reference Carbonneau, Lane and BergeronCarbonneau and others, 2004; Reference Verdu, Batalla and Martinez-CasasnovasVerdu and others, 2005; Reference Black, Carbonneau, Church and WarburtonBlack and others, 2014). This shortcoming precluded the use of UAV imagery for input to photo-sieving, and the subsequent extraction of complete grain-size distribution curves from these data. Potential solutions for obtaining spatially selective grain-size distribution information from extensive aerial photographic datasets lie in the use of digital cameras with greater sensor resolutions, decreased survey altitudes (possible with multi-rotor platforms for complex topography), or a combination of the two approaches in order to decrease the minimum identifiable grain-size fraction. In this study, survey altitude was constrained by the flight plan and operational banking angle of the UAV, which necessitated deployment above the hillside spurs bordering the embayment. We instead used patch-scale, terrestrial photography in which individual grain outlines are clearly identifiable.
Options for optimizing the accuracy and resolution of D 50 mapping also exist. The point-cloud decimation software, ToPCAT, which was used to calculate the detrended standard deviation of local point elevations, extracts data from within predefined gridcells that contain 3-D point data (Reference Rychkov, Brasington and VericatRychkov and others, 2012). The presence of individual large clasts, located in areas of otherwise comparatively fine-grained material, might result in the mischaracterization of the surface topography. Alternative methods for deriving surface roughness metrics might include the use of a ‘roving window’ approach (e.g. Reference Haubrock, Kuhnert, Chabrillat, Güntner and KaufmannHaubrock and others, 2009; Reference SmithSmith, 2014), which aggregates data within a predefined or variable radius around individual 3-D points, and has the potential to produce higher-resolution topographic metrics.
Application to glacial geomorphological process analysis
At the patch scale, the analysis of clast morphology and alignment provides more information than that decipherable from grain-size distribution data alone. Detrended 3-D point data may be used to extract descriptors of surface texture, such as dominant clast inclination angles (e.g. Reference Hodge, Brasington and RichardsHodge and others, 2009a,Reference Hodge, Brasington and Richardsb), while the automated extraction of 2-D clast orientation vectors, also provided as output from photo-sieving, may provide insights into characteristic styles of deposition, or post-deposition reworking that may be indicative of, for example, solifluction. At the site scale, the straightforward construction of hillshaded DEMs from raw or generalized 3-D point datasets can reveal levels of topographic detail that far surpass those recoverable from coarser topographic data products (e.g. Reference Van den EeckhautVan den Eeckhaut and others, 2005), such as satellite-derived DEMs, and which may significantly augment field-based geomorphological observation and mapping.
Analysis of high-resolution DEMs permits the quantification of landform geometries across a range of scales (Reference Passalacqua, Hiller and TarolliPassalacqua and others, 2014, Reference Passalacqua2015; Reference TarolliTarolli, 2014), while the derivation of median grain-size data from UAV-SfM modelling has the potential to provide a new perspective on the spatial distribution of bulk sedimentological characteristics of glacial landforms. A hillshaded perspective of the moraine UAV-SfM DEM which serves as the background to Figure 9b provides enough topographic detail to support the identification of a range of glacial features including, from the largest to smallest, individual moraine ridges, ice-marginal thermokarst topography, crevasse traces and troughs, gullies on the flanks of the larger moraines, and concentrations of boulder erratics; the latter may be explicitly highlighted using D 50 thresholding (Fig. 9b). The interpretation of such data may aid the reconstruction of active or former glaciological flow directions (e.g. Reference Evans, Livingstone, Vieli and Ó CofaighEvans and others, 2009; Reference Sugden, Fogwill, Hein, Stuart, Kerr and KubikSugden and others, 2014). Finally, the acquisition and differencing of multitemporal, fine-resolution DEMs permits the quantification of 3-D patterns and rates of surface evolution that may provide crucial insights into process–form relationships that are difficult to quantify through the use of individual datasets (e.g. Reference James and RobsonJames and Robson, 2012; Reference DunningDunning and others, 2013; Reference Irvine-Fynn, Sanz-Ablanedo, Rutter, Smith and ChandlerIrvine-Fynn and others, 2014; Reference StainesStaines and others, 2014; Reference Williams, Rennie, Brasington, Hicks and VericatWilliams and others, 2015).
Conclusions
This study has demonstrated the potential of SfM methods for classifying the grain-size distribution of unconsolidated glacial surface sediment at the patch- and site scales across an Antarctic blue-ice moraine. Manual quantification of grain-size distribution information from exposed, unconsolidated glacial surface sediment is labour-intensive, physically intrusive and subject to operator bias. By comparison, contactless sedimentological surveying methods, including automated photo-sieving and the analysis of surface elevation statistics of fine-resolution 3-D point datasets, are rapid and equally applicable to the patch- or site-scale observation of glacial sediments. Ground-based SfM and TLS were used to quantify 3-D patch-scale surface topography, with SfM reconstruction outperforming TLS in terms of absolute data density and spatial coverage.
Automated photo-sieving of SfM orthophotography was used to quantify the grain-size distribution for 12 patches of surface sediment. Upscaling from patch- to site-scale sedimentological characterization was achieved through the statistical analysis of a site-scale UAV-SfM surface elevation dataset to derive a relationship between the median grain size and topographic roughness. This relationship was applied to a UAV-SfM DEM of the entire moraine complex. The resulting maps, which characterize the median grain-size fraction across the site, reveal links between moraine geomorphology and the spatial distribution of moraine sediment facies.
Acknowledgements
The research was funded by the UK Natural Environment Research Council (Research Grants NE/I027576/1, NE/ I025840/1, NE/I024194/1, NE/I025263/1). M.J.W. acknowledges Martin Detert for assistance with BASEGRAIN parameterization. We thank the British Antarctic Survey for field logistics support.
















