1. Introduction
Reference Nye and FrankNye and Frank (1973) have proposed that temperate glacier ice should be permeable to water flow because of a three-dimensional network of veins lying along three-grain intersections. There are a number of processes in glaciers in which intergranular water flow could play an important role. Intergranular water flow is one possible route by which surface water can reach the glacier bed. The downward percolation of water could transport heat by advection and provide an internal heat source coming from viscous dissipation. It could dissolve and transport gases and soluble solids, thus affecting the texture and chemistry of the glacier ice. The vein network would provide the only means by which water produced by the mechanical production of heat could be drained from the ice. Furthermore, the veins may be important in the formation of larger conduits in the ice such as discussed by Reference RöthlisbergerRöthlisberger (1972) and Reference ShreveShreve (1973).
The existence of veins in ice samples has been observed (Reference Nye and FrankNye and Frank, 1973). However, the existence of a connected three-dimensional network has not been established to exist in flowing glacier ice, and Reference LliboutryLliboutry (1971) and Reference Nye and MaeNye and Mae 1972 have given reason to doubt its existence because of complications in texture and non-hydrostatic stress. Even if the vein network is essentially complete, it is not possible to deduce the amount of water How through it without knowledge of the size of the veins, a quantity which present theories are not capable of predicting.
The purpose of this paper is to present observations of the liquid and gas phases in core samples from Blue Glacier, Mt Olympus, Washington, U.S.A. The glacier is described by Reference KambKamb 1959, Reference Allen, Alien, Kamb, Meier and SharpAllen and others (1960), Reference LaChapelleLaChapelle 1965, Reference CorbatóCorbató 1965. Reference HarrisonHarrison 1972 and Reference Meier, Meier, Kamb, Alien and SharpMeier and others (1974). The coring was done during the third and fourth weeks of August 1972 at a site slightly below the usual late-summer snow line. The site was at an elevation of about 1590 m near the 1961 location of the bore hole S2 of Reference Shreve and SharpShreve and Sharp (1970, p. 67). A year earlier sensors had been placed at a site roughly 30 m down glacier in a related experiment to measure deep in situ temperature (Reference HarrisonHarrison, 1975[b]). Samples were examined at about 1.5 m intervals to a depth of about 60 m or about a quarter of the total depth.
Experimental methods are described in Section 2. The observations and their relation to in situ conditions are found in Sections 3 and 5; some vein properties used in subsequent sections are collected in Section 4. A tentative picture of the water flow through veins and larger-scale features is given in Section 6.
2. Methods
Cores were obtained with a thermal core drill yielding cores 0.15 m in diameter and 1.6 m in length (LaChapelle and Taylor, unpublished). Immediately upon removal from the core barrel, cores were covered to prevent exposure to short-wave radiation and carried to a nearby snow cave. There a sample about 0.1 m thick was cut perpendicular to the axis of each core. Observations began typically within 20 min of breaking the core off at the bottom of the hole and within 5 min of its arrival at the surface. Observations were continued usually for about one hour.
Microscopic observations were made with a stereoscopic microscope capable of magnifications of 6 to 100 times. A special stand allowed placement of large samples under the micro scope. The distance from the objective lens to its plane of focus was 90 mm in air, which permitted examination of features well into samples. A beam splitter with 35 mm camera mount allowed simultaneous visual observations and photography. Size measurements could be made with a calibrated reticle.
The microscope and sample were positioned on a transparent table with illumination provided by a 100 W bulb mounted about 0.2 m beneath the table surface. In most cases oblique transmitted light provided the highest contrast and best viewing. In the upper part of the sample, where most observations were made, calculation of the rate of absorption of radiation indicates that at most 10−3 fractional volume of the ice could be melted per hour of continuous illumination. To minimize internal melting from the lamp, it was turned on only when measurements were being made, and an aperture was used so only a small part of the sample was illuminated at any one time.
Thin sections of the core cross-sections were made from samples cut near the microscope samples. They were photographed under crossed polaroids to record textural information. Some thin sections and etched surfaces were also examined directly.
3. Observations on samples
3.1. Texture
The number of grain-boundary intercepts per unit length of randomly oriented lines was measured on thin sections and etched surfaces. The reciprocal is denoted by a and is a standard definition of grain size (Reference McLeanMcLean, 1957, p. 112). The number of three-grain inter sections crossing unit area of section was also counted. This quantity is denoted by n. As long as the grain texture is isotropic or n is counted on a number of random sections, the length i of three-grain intersections per unit volume is given by l = 2n (Reference Smith and GuttmanSmith and Guttman, 1953).
Although there is no unique relationship between a and n one expects for dimensional reasons that n = k/a 2, where k is a textural parameter. On six thin sections which were measured with special care к ranged from 0.8 to 2.1. Since water content and water flow are more directly related to n than a, n is used in most of the subsequent discussion, and a corresponding approximate grain size is based on a single value of к = 2.
As expected from Reference Allen, Alien, Kamb, Meier and SharpAllen and others (1960), the samples usually fell into two basic textural types: fine ice with n ≈ 5 × 105 m−2 (a ≈ 2 mm) and coarse ice with 103 m−2 < n < 2 × 104 m−2 (10 mm < a < 50 mm). Ice of intermediate or mixed grain size was also present but in smaller amounts.
Over the depth range of the core hole, three distinct structural zones could be distinguished. The highest zone was a layer of snow about 2 m deep. Between the snow and depth 27 m there was a zone of mostly fine ice with only weak foliation. There were local occurrences of mixed or coarse texture. Most of the ice was bubbly, but there were several 1 to 2 m lengths of perfectly clear core from depths of 10, 20, and 23 m. Below 27 m, there was a transition over several meters depth to a third zone of mostly coarse-grained bubbly ice with well developed foliation dipping at angles of about 75° at 30 m depth and 60° at 60 m depth. In this zone, clear ice was restricted to relatively thin layers in the foliation pattern.
Densities of 13 typical coarse bubbly ice samples were measured and 0.90 Mg m−3 was found to be characteristic. Distributions of bubble size were measured in three typical coarse bubbly samples; these gave average bubble diameters ranging from 0.5 to 1.2 mm. An additional measure of bubble content in two coarse bubbly samples was determined by counting the number of bubbles intersecting a line of known length randomly placed on a plane section. The average bubble spacing on such lines was 25 mm for a sample with a = 21 mm and was 15 mm for a sample with a = 14 mm.
In order to investigate the distribution of bubbles with respect to grain boundaries, the number of bubbles touching the trace of grain boundaries was also counted for these two samples. In each case the length of grain boundary trace was also estimated by the method of Reference Smith and GuttmanSmith and Guttman 1953 using three orientations of a square grid with mesh about equal to a. The resulting estimates of the average spacing of bubbles along grain boundary trace were somewhat smaller (33% and 45%) than along random lines. This suggests some concentration of bubbles along grain boundaries, but with so few samples it is difficult to say whether this is characteristic.
3.2. Configuration of the liquid and gas phases on a granular scale
Veins of water were visible in all samples. An example of fine-grained clear ice is shown in Figure 1. As envisaged by Reference Nye and FrankNye and Frank 1973, the veins were on three-grain inter sections and formed a three-dimensional network with four veins coining together at each four-grain intersection. Occasional three-grain intersections in some samples did not have continuous veins lying on them. Figure 2 shows an example in which a four-grain intersection had only two visible veins running into it. The other two three-grain intersections were marked by pods of liquid. Such three-grain intersections without veins were relatively infrequent in the fine-grained ice. Although there is not a precise one-to-one correspondence between continuous veins and three-grain intersections, it seems to be a good approximation for practical purposes. Continuity of the vein network in coarse-grained ice could not be checked because tracing of the network topology over the scale of the grain size was hampered by the large dimensions and poor visibility caused by bubbles. A few instances of an apparently high proportion of missing veins were seen in coarse clear ice. An example is shown in Figure 3.

Fig. 1. Fig. 1. Veins in fine-grained ice collected from 10 m depth.
Liquid was also found to exist in many samples as lenses on grain boundaries and in irregular shapes as shown in Figure 3. Lenses on grain boundaries have been observed previously in laboratory-grown ice (Reference Nye and MaeNye and Mac, 1972). The lenses were not concentrated near three-grain intersections, but were usually distributed over particular grain faces. Lenses were sometimes associated with discontinuous veins as in Figure 3; however, there was not a one-to-one correspondence. Lenses were observed close to veins of typical size, and discontinuous veins without nearby lenses were seen. The proportion of grain faces with lenses to the total number of faces in any volume containing a Large number of crystals was always small. In a given local region, grain faces of differing orientation had lenses, indicating that there was not a very strong preferred orientation.
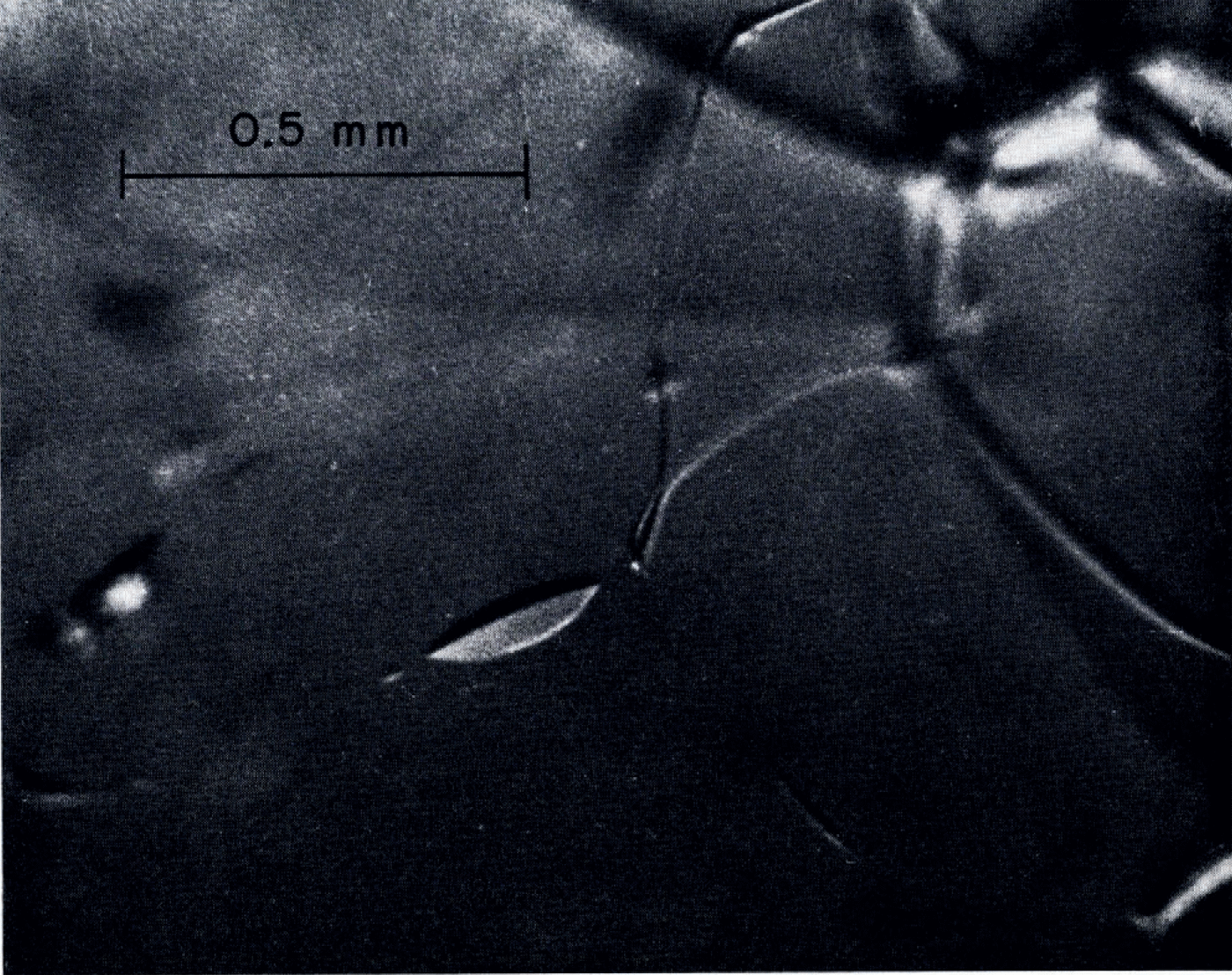
Fig. 2. Discontinuous veins. Note four-grain intersection with only two veins coming into it and pods of liquid on the apparent traces of the other two three-grain intersections.

Fig. 3. Fig. 3. Liquid lenses and other liquid inclusions in a thin layer of course-grained clear ice from 13 m depth.

Fig. 4. Veins in fine-grained bubbly ice collected from 10 m depth.

Fig. 5. View of vein with the width shown. The apparent width, of this particular vein is much larger than average, but the visual appearance is characteristic.
An example of bubbly ice is shown in Figure 4. Columns of air extend into veins from air bubbles touching the vein network. Bubbles isolated from the veins also were present, especially in coarse ice. These bubbles contained some liquid. Liquid in bubbles has also been observed by Bader 1950. The configuration of air in the veins and liquid in the isolated bubbles changed rapidly with time.
3.3. Size of veins
Vein widths d a were measured using a calibrated reticle. Figure 5 shows an example of a water-filled vein and the dimension which would be specified as the width. The edges were not sharply delineated lines, and the visible width depended somewhat on the microscope focus and illumination angle, but width could be chosen consistently to within about 5 to 10 μ m. When gas occupied a vein, the gas column was sharp and its width could easily be measured.
The details of the vein cross-sectional shapes were not examined. Qualitatively they had the triangular c ross section exp ected from the boundary-energy relationships as discussed by Nye and Frank ( 1973, p. 158, fig. 2). Nye and Mae (1972) indicate that the dihedral angle 2 Θ between the two solid- liquid interfaces at a vertex is typically 32°. This d etermines the cross-section shape. Geometrical parameters of interest can be expressed in terms of the vertex-to-vertex distance d, the root-mean-square radius of the vein T, or the cross-sectional area A (Table I ) .
Table I Geometrical Paramete RS of Veins Evaluated for Dihedral Angle 2 e = 0.56 rad (32°)


Fig. 6. Average width da observed in samples collected from various depths. Bars show root-mean-square deviation of measured sizes from mean for the sample. Solid circles represent data measured within the first hour after collection. Open circles give measurements after about one day.

Fig. 7. Frequency of vein widths measured within one hour of collection. Local minima at half-integral reticle units larger than one exist because large veins were measured only to the nearest reticle unit in some samples.
Figure 6 shows the means and standard deviations of the width distributions for samples collected from various depths. Distributions measured within about the first hour and measured alter one day are shown separately. Samples originating below 7 m showed no significant differences in vein size; nor was there any apparent correlation of width with grain size or bubble content. Figure 7 shows the combined distribution of widths measured within the first hour of collection for all samples below 7 m. From this distribution, we find r> = 13 × 10−16 m, (A) = 6.6 × 10−10 m2, and (Az) = 1.2 × 10−18 m4.
3.4. Larger-scale features
Large-scale tubular features, suggestive of conduits, were seen in two cores. One such feature with a diameter of about 1.9 mm was seen in a core cross section at 9.6 m depth. Several others with diameters of a few millimeters were seen in a vertical slab (30 mm X 150 mm x 0.9 m) cut parallel to the core axis at 20 m depth (Figure 8). In this case two or possibly three junctions of upward branching could be seen; this fits the upward branching “arborescent” network of conduits envisaged by Reference ShreveShreve 1972. The cross-sections of these features were irregular as a result of rounded protrusions of the bounding crystals toward the axis of the tube.

Fig. 8. Tubular features in a slab of mostly fine-grained, clear ice from 20 m depth. Up is lo the left. White marks are spaced 100 mm apart.
4. Properties of veins
Some properties of the veins relevant to subsequent calculations in Sections 5 and 6 are considered here.
4.1. Water transport
The water flux Qv through a vein in the presence of an effective pressure gradient F (i.e. gradient of pressure and gravity potential) can be estimated by an approach similar to that of Reference Nye and FrankNye and Frank 1973. For a circular tube with cross-sectional area A,
where η = 0.57 × 10−15 bar year is the viscosity of water and X’ = 1. Equation (1) can be used for a vein if X’ is chosen to account for the non-circular cross section. A standard argument gives X’ ≈ (r/2rh)2 where rh, is the hydraulic radius. From Table 1 we find that X’ = 2.4 which gives flux approximately as
and average velocity in a vein
when meter-bar-year units are used.
The flow through a system of veins of isotropie texture is considered next, now assuming that F represents the effective pressure gradient averaged over several grain sizes. In a vein inclined at an angle ψ to F, the flux parallel to F, is Q v cos ψ. If we average over all directions, ‹COS ψ› = ½ Therefore, the flux q per unit area along F is given by
where n is the number of channels crossing unit area and it is assumed that none of them is blocked. The vein volume is lA, where l is the vein length per unit bulk volume. An average velocity u may be defined by u(lA) = q. Since l = 2n (Section 3.1),
Equations (3) are in meter-bar-ycar units.
4.2. Thermal Properties
The equilibrium temperature T at a vein wall is given by
where δ = 0.0100° C is the triple-point temperature, β = (I/ρ—I/ρ) T 0 /h = 0.00742 deg bar−1 is the Clausius-Clapeyron slope, α = (T γSL/h ρi) (√(A/r p) = 0.82 × 10−8 deg m represents the effects of phase-boundary curvature expressed in terms of √A rather than radius of curvature rp , and θ is the temperature depression by dissolved impurities. The numerical values are found from the gas constant R = 4.62 × 102 J deg − kg−1, T 0 273 deg, the liquid-solid surface energy γSL = 0.034 J m−2 (Reference Ketcham and HobbsKetcham and Hobbs, 1969), the specific latent heat h = 3.34 × 105 J kg−1, the density of ice ρ i = 0.92 Mg m−3, the density of water ρw = 1.00 Mg m−3, and ⊡ A/rp = 0.270 from Table . For some purposes it is useful to express θ as
where C l is proportional to the total dissolved impurity content per unit length of vein. On the scale of the vein diameter of several tens of micrometers, impurity diffusion evens out the concentration within seconds. Therefore Equation (4b) applies 10 the complete perimeter of a vein unless extremely rapid melting or freezing is taking place.
4.3. Capillary effects
In Appendix A it is shown that the gas-liquid pressure difference in a vein partially occupied by gas is close to pc = 2γLV/r” where γLV = 0.076 J m −2 is the liquid-vapor surface energy. This gives
in meter-bar units.
5. Relation to in situ conditions
\The relation between conditions in the ice as seen under the microscope and the in situ conditions in the glacier, where the stress and temperature environments are different, is considered in this section.
5.1. Bubbles
The bubbles isolated from the veins always contained water at the time of observation, but the in situ liquid content was probably small or zero. More details are given by Reference RaymondRaymond (in press).
The pressure in the veins probably dropped from its in situ value to near atmospheric pressure while the core was being raised to the glacier surface. The gas bubbles touching veins should have expanded into the vein network to reach the sample surface and relax the bubble pressure. During the initial stages of this process, Equation (2b) and the pressure gradient expected from the in situ bubble pressures and the core size predict that water should have been forced out of the veins at speeds in excess of millimeters per second. This is so rapid that the process probably happened progressively as a core was brought to the surface. At the time of observations, some sporadic motion of the ends of gas columns still was occurring but was less than about 1 mm s−1. This was caused possibly by small residual excess gas pressure, readjustment of capillary forces with vein-size change, or by exsolution of dissolved air. During the large initial pressure relaxation, the expulsion of gas was possibly along favored vein paths because of the range in vein size (Fig. 7), and the vein liquid being forced toward the core exterior probably would have been trapped in intervening bubbles. There fore, the process was not necessarily accompanied by a gross expulsion of the original vein liquid.
The pressure relaxation could have produced air columns extending from bubbles into veins as seen in the samples. It is doubtful that this was the in situ configuration because it cannot be in local thermal equilibrium. Where such columns exist, the air pressure in the bubbles exceeds the vein water pressure by p c. (Section 4.3). From Equations (5) and (4a) the temperature depression in the bubbles from p c is βpc = 2.0 × 10−8/√A this is larger than the temperature depression from wall curvature in the veins given by α/√A ≈ 0.82 × 10−8/√A. If diffusion of impurities can occur and even out differences in concentration between the vein liquid and any liquid on the walls of bubbles, then bubbles would be colder than veins. At the other extreme, if gas only partially fills the volume of a bubble cavity, then the thermal effect of capillary pressure is eliminated and the veins are colder than the bubbles. A stable configuration is probably an intermediate one in which the gas-liquid meniscus lies within the bubble-vein orifice al a location such that its curvature produces a pressure difference which just balances the effect of vein-wall curvature.
5.2. Lenses and other isolated liquid inclusions
Because of the elastic anisotropy of the ice crystals, it seems probable that certain sub-volumes and grain faces continued to experience compressive stress for some time after the core was raised to the glacier surface and the exterior pressure had dropped. In such zones the pressure in isolated inclusions could have been larger than the pressure in the veins or on the sample exterior. Heat flow from the veins or the exterior could have caused the growth of lenses on grain boundaries (Reference Nye and MaeNye and Mae, 1972) or liquid pods on certain three-grain intersections for which grain-boundary energy relationships preclude the existence of stable veins. Because the ice was initially cold and the veins contained impurities, the growth of such inclusions could have been blocked at first. However, the ice and veins could have warmed rapidly as is discussed in Section 5.3.
If the residual elastic compressive stress on a grain face is on the order of one bar and the corresponding elastic stress can be relieved by relative displacements on the scale of the grain size (c. 10−2 m), then the stress could be relieved by melting a 1 μm layer of water averaged over the grain face. From Reference Nye and MaeNye and Mae (1972, p. 93 and 94) one finds that the average thickness of a lens is about 0.07 times its diameter, which for lenses of diameter about 0.1 mm (for examples as shown in Fig. 3) amounts to 7 μm. This suggests that a considerable fraction of a grain face could have been covered by lenses before the driving compressive stress was relieved by the melting. The existence of lenses on grain boundaries of various orientations as seen in the samples (Section 3.2) gives support to this mode of lens formation. On the other hand, no concentration of lenses near the sample surface or veins was noticed, but this might be expected as a result of rapid formation by the above process. It seems difficult to draw any certain conclusions about the in situ existence of lenses.
5.3. Veins
Redistribution of heat within a sample, conduction of heat into the sample from its surface, and exchange of impurities, could have caused vein sizes to change before they were measured. The relaxation process can be discussed in terms of Figure 9, in which the combined temperature depression θ’ of a vein from dissolved impurities and vein-wall curvature given by Equations (4)
is shown as a function of A for various values of impurity per unit length of vein C l. The vein size A is about 6.6 × 10−10 m 2 in the samples, and the sample vein properties lie somewhere on the vertical line marked A sample. The in situ temperature T is known below a depth of about 6 m (Reference HarrisonHarrison, 1975[b]) and the in situ θ’ can be estimated from Equation (4a) and the assumption that vein pressure is equal to the mean stress in the ice. A very small vertical strain-rate (Reference HarrisonHarrison, I975[a]) provides evidence that the ice mean stress is close to the overburden pressure. This gives an in situ θ’ ranging from 0.020 to 0.028 deg depending on depth and time; θ’ = 0.024 deg is reasonably characteristic of the whole depth range. The in situ vein properties lie near the horizontal line marked θi’.
Relaxation without impurity exchange. If the impurities do not move significantly along the length of veins by diffusion or water flow during the relaxation process, then it is reasonable to assume that C l remains constant. In this case the vein properties change by displacement along the lines of constant C l shown in Figure 9.
The initial stages of the relaxation are associated with pressure drop in the veins as a core is raised from depth to the surface of the glacier as discussed in Section 5.1. This raises the vein wall temperature above the temperature of the surrounding ice and the resulting heat flow causes freezing on the vein walls corresponding to displacement along a line of constant C l upward to the left. This process of local redistribution of heat is analysed in Appendix B. The process should have been complete within several minutes after the drop in pressure; it was probably already complete before samples were cut from the core. The resulting change in vein size and temperature depends on texture and the pressure drop. For samples collected near the glacier surface, there is little pressure drop, the changes are small, and the vein properties would still plot near the horizontal line ρ,’ in Figure 9. The possible vein size change and the corresponding change in ρ’ are substantial for samples collected from 60 m, and are shown by curves (long dashes in Figure 9) for a fine texture (l = 106 m −2, a ≈ 2 mm) and a coarse texture (l = 104 m−2, a ≈ 20 mm). For example, fine-grained ice from 60 m with initial vein properties corresponding to P1 would change to P2.
On a somewhat longer time scale, heat conducts into the sample from its surface, which causes melting of the veins and displacement along a line of constant C l downward and to the right. Eventually the inward conduction of heat ceases when θ’ becomes equal to the temperature depression θs from impurities in the liquid layer on the exterior surface, in which case temperature gradients have been eliminated. Because the bulk impurity content of the ice was measured to be extremely small, it is likely that θs is determined by the amount of air in solution at ambient, atmospheric pressure (about 0.82 bar) which gives θs’ = 0.0020 deg. This is plotted as the horizontal line θs’ on Figure 9. For example, the vein properties would relax by local redistribution of heat to P2, progress back to P1 pass through P3, and eventually reach P4, where relaxation would stop.

Fig. 9. Relationship between θ’ and A for various values of Cl. Units of Cl are deg m2. θ1,’ and θs’ are thein situ and sample surface values of θ’ . Long dashes give vein properties after completion of the adiabatic pressure relaxation for fine-grained ice (fn, 60 m) and coarse-grained ice (crs, 60 m) originating at 60 m. Short dashes give properties expected after 30 min 5 mm into sample for grained ice from near the surface (fn, o m), fine-grained ice from 60 m (fn, 60 m), coarse clear ice from near the surface (cc, o m), and coarse bubbly ice from 60 m (cb, 60 m). P1,, P2, P3, P4 represents a possible relaxation path for fine ice from 60 m depth. Other inclined dashed lines give possible relaxation paths for other textures and origin depths.
With these constraints on the initial and final values of θ’ and on the relaxation path, the in situ vein size can only be in the range L to U for ice originating near the surface, L to Ul for fine ice from 60 m, and L to Uc for coarse ice from 60 m. Numerical values of these limits are listed in Table II, columns 1 and 2.
In order to narrow the limits further it is necessary to know the time scale of the heating. This was studied by solution of the equation of thermal diffusion with a source term which accounts for the heat of fusion associated with change in vein size (Appendix C). The vein properties after the pressure relaxation provide initial conditions, and the temperature on the external surfaces provides boundary conditions. For simplicity, the circumferential surface of the disk-shaped samples was neglected and the solution was carried out for slab geometry. The solutions show rapid vein size changes during the first several minutes and strong gradients in the first several millimeters below the surface. At later times and greater depth the variations are much less pronounced and are small enough to be compatible with the apparent lack in the samples of a depth gradient and lime dependence during the initial hour of observation (Section 3.3).
Table II Estimates of in situ vein size and expected K/UX
Column 2: Upper limit assuming constant C l.
Column 3: Estimated size from thermal diffusion assuming C l constant.
Column 4: Estimated size from adiabatic relaxation by replacement of impurities.
A s = 66 × 10−10 is size observed in samples collected from depths greater than 7 m.

* assuming bubble pressure is atmospheric pressure.
† clear ice.
‡ bubbly ice.
A typical depth below the sample surface for measured veins is about 5 mm, and time of measurement is about 30 min after sample collection. Based on the above limits on in situ size, the possible range of vein properties predicted at this depth and time are represented as curves (short dashes) in Figure 9 for various textures and depths of origin. For example, fine-grained ice originating from 60 m and initial size A = 1.9 × 10−10 m2 would follow the path P1, P2, P3 and would have a size about equal to the observed size at the time of observation. Very coarse clear ice relaxes rapidly because of a low water content, which causes the contribution from the internal source term to be small. At the other extreme, coarse bubbly ice does not heat up above the temperature depression caused by air pressure in the bubbles isolated from the veins, and relaxation of the bubble pressure by heat conduction or mechanical effects is very slow (Reference RaymondRaymond, in press). The initial bubble pressure is probably near the ice overburden pressure, which for 60 m origin depth gives θ’ = 0.049 deg and this changes very slowly during the first hour. Table II, column 3 gives values of in situ size expected from this model for several textures and depths of origin.
Adiabatic relaxation by rapid replacement of impurities. At the opposite extreme we may consider a case where the liquid in the veins not only experiences an abrupt pressure drop but also a drop in impurity content to a concentration corresponding to that in the layer of water on the external surface. Because the diffusivity of typical soluble impurities in water is small in comparison to the effective thermal diffusivity of the ice, diffusion is not rapid enough to exchange impurities before significant heat flow from the surface has occurred. However, water flow could possibly replace the vein water rapidly and continuously. If this happens, the vein would be held at a temperature depression θ’ corresponding to θ s except for a small contribution due to vein-wall curvature. The ice could be heated up nearly to its final equilibrium temperature by freezing in the veins and local redistribution of heat on a granular scale. The net effect would be reduction in vein size, and is worked out in Appendix B, assuming no heat flows in from the sample surface. This gives estimates of in situ sizes shown in Table II, column 4. The time scale for this to happen is similar to that for the pressure relaxation considered above and in Appendix B, but the size and temperature changes are larger because the impurities are not permitted to concentrate in the shrinking veins.
If the water-drainage velocities were too slow to affect the bulk core before a sample was cut from it, which seems likely, then the replacement of impurities beneath the upper flat surface of a disk-like sample (Section 2) would not start until it was cut out. Even if the sub sequent replacement of impurities were essentially instantaneous, heat flow from the sample surface would contribute to the heating of the ice within several grain diameters below the surface. The estimates in Table II, column 4 apply only at greater depth in the sample.
Discussion. If conduction from the surface has already heated the ice and diluted the vein liquid by the time surface liquid arrives, there will be little effect from motion of impurities. A rough measure of the time needed to change significantly the temperature at distance x below the sample surface by conduction is x2/κ where κ is the effective thermal diffusivity (Reference Carslaw and JaegerCarslaw and Jaeger, 1959, p. 60). The corresponding time for penetration of surface water to this depth is x/u, where u is the water drainage velocity. Therefore, when x2/κ ≪ x/u or κ/xu ≫ 1, the effects of impurity replacement should be small. We may expect that κ/xu = 1 represents a transition.
Appendix C gives the dependence of κ on A, l, and θ’. The water drainage velocity can be estimated from Equation (3b) with the effective pressure gradient F = (ρw—ρ1)g = 0.01 bar m−1. This is the average value of F if the sample is supported by a water layer at its base, and the water layer on the upper surface is thick enough to eliminate capillary effects there. Since a sample could be partially supported on local points of contact, F could be somewhat larger. Values of κ/xu are shown in Table II for the various textures and estimates of in situ vein size assuming θ’ is the in situ value and x is 5 mm.
For fine-grained ice κ/xu ≫ 1 for any of the estimated in situ sizes (Table II). This would be true even if F and the drainage velocity were somewhat larger than assumed. Therefore the adiabatic relaxation by replacement of impurities should not occur, and the assumption of constant Q is reasonable. We can be fairly confident that the upper limits to vein size listed in Table II, column 2 are valid. The more refined predictions of in situ size in Table II, column 3 are consistent with the observational and theoretical constraints which we have discussed, but there are factors which have not been taken into account and which could significantly affect the time scale of the relaxation and those predictions. Examples are: the effect of liquid at locations other than veins, some effect from water flow, and the possibility that in situ θ’ is different from that assumed. Therefore we choose to limit our conclusions to the upper limits of column 2.
The same reasoning can be applied to coarse ice, but in this case the values of κ/xu are not so large. The values in Table II, column 4 are close to or even smaller than one. The relaxation of veins of these in situ sizes would no doubt be significantly affected by water motion; however, the values of κ/xu seem still too large to permit the dramatic freezing that would be needed to give the size seen in the samples. Furthermore in coarse ice the characteristic measurement depth of 5 mm into the sample is less than the grain size, and the in situ sizes listed in Fable II, column 4 would be over estimates even if κ/xu were zero as discussed previously. Given that the in situ size must have been significantly smaller than listed in column 4 of Table II, then κ/xu would have been greater than one. This leads to the conclusion that the sizes listed in Table II, column 2 are also reasonable upper limits in the case of coarse ice.
On a time scale longer than one hour, water flow and diffusion must be important. The expected drainage velocity for the vein size existing in the samples is about 6 mm h−1 and would tend to keep θ in the veins equal to ρs. Because of the vein-wall curvature, the veins would be colder than the surface. Solution of the heat-flow equation with the source term from vein size change evaluated from Equation (4a) and θ constant (Appendix C) predicts an increase in vein area of about 2 to 5 times over 24 h. This could explain the observed increase in vein size after one day (Figure 6).
6. Constraints on the pattern of water flow in the glacier
6.1. Limits on intergranular flux in clear ice
Reference Nye and FrankNye and Frank 1973 assume that the pressure of water in veins is equal to the mean ice pressure. Reference ShreveShreve 1973 has derived the resulting effective pressure gradient F under sloped ice surfaces, which for the core site gives F = 0.013 bar m−1. Upper limiting values for the intergranular water flux per unit area can be calculated from Equation (3a) and this value of F, using the upper limiting values of A determined in Section 5.3 (Table II, column 2). The results for typical fine and coarse ice textures are listed in Table III, column 2.
Table III Upper limits to vein water content and flux density

6.2. Effect of bubbles
The in situ configuration of gas bubbles touching veins expected from Section 5.1 agrees with the view of Reference LliboutryLliboutry (1971, p. 20, fig, 2). Such bubbles constitute local blockages of veins which can support pressure differences up to the capillary pressurepc. Since by Equation (5) pc is about 0. 1 bar or more for the expected in situ vein sizes, the bubbles are closely spaced, and the effective pressure gradient is only about 0.01 bar m−1, it seems unlikely that such pressure differences would be achieved in typical circumstances in the glacier.
A simple statistical model developed in Appendix D gives the fractional reduction in ice permeability in terms of the average spacing s of bubbles along veins and the average distance b between four-grain intersections. If bubbles are randomly distributed in the ice volume, then from Reference LliboutryLliboutry (1971, p. 19}

where R is the average bubble radius, and v is the fractional void volume. Although the two bubble counts reported in Section 3.1 suggest that bubbles were not strictly randomly distributed, there probably are not any large errors from this source and Equation (8) should give a reasonable estimate. The density and bubble sizes measured on coarse bubbly ice (Section 3.1) give s about 20 mm. This also agrees with the average spacing of bubbles on random lines (s equals 25 mm and 15 mm) measured on the two coarse bubbly samples (grain size a equals 21 mm and 14 mm) which were measured in more detail (Section 3.1). One also expects that b ≈ a. Therefore in typical coarse bubbly ice b/s is on the order of 1 or larger, in which case the results of Appendix D predict that bubbles substantially reduce the water flux. In fine-grained ice the effects of bubbles are much less. Theoretical fractional reduction in water flux by bubbles is given in Table III, column 3 for various grain sizes assuming s = 20 mm and b = a.
6.3. General pattern of flow and discussion
At the core-hole site, water production averaged over a typical day was about 25 mm d−1(or 9 m a−1). The pattern of ice texture(Section 3.1) and the limits on intergranular water flow (Table III) place some constraints on how this melt water moved.
The absence of any surface pools or streams indicates that all of the melt water penetrated into the snow. Fine ice with the vein size seen in the sample from 4.8 in would transport a flux per unit area of about 10 m a−1 according to Equation (3a). This suggests that much of the melt water could have penetrated into the uppermost ice and agrees with the observations of Reference WakahamaWakahama and others (1973 ), who concluded that the ice near the surface of Menden hall Glacier was permeable. However, once below 7 m depth in the zone of mostly fine ice (a ≈ 2 mm), the intergranular flux per unit area would be no greater than 0.1 m a−1 (TableIII). Yet deeper in the zone of foliated coarse ice, it is likely that the intergranular flux per unit area would be even smaller because of the much lower density of three-grain intersections and the blockage of veins by bubbles (Table III).
Since only a small fraction of the daily melt water can penetrate below a depth of about 7 m on an intergranular scale, most of it must run laterally through the snow or the permeable near-surface ice to cracks or conduits. The fact that conduit-like features were observed in the small volume represented by the core and the fine scale of the branching (Section 3.4) suggests that the density of conduits could be as high as several per square meter near the surface. A rough estimate of the water How through such conduits suggests that a density of several to several tens per square meter would be sufficient to transport all of the daily melt. Therefore, it seems possible that much of the melt water could have penetrated into the ice locally, although not on an intergranular scale.
This picture of water flow is similar to the theoretical predictions of Reference Shreve and SharpShreve 1972, but the concentration of the surface melt-water flux from the fine-scale vein network to the larger-scale conduits occurs in a thin layer just below the surface. The small residual intergranular flux of less than 0.1 a−1 during the height of the melt season suggests that the vein network does not respond to the availability of surface melt water. This could be a consequence of a very small in situ vein size and water velocity, in which case the propagation of kinematic waves hypothesized by Reference Nye and FrankNye and Frank 1973 would also be slow. However, it might also be caused by the tendency of water flux to concentrate from smaller into larger conduits (Reference Shreve and SharpShreve, 1972; Reference RöthlisbergerRöthlisberger, 1972) and thermal constraints on the manner in which clean surface melt water can enter into the ice. The nature of the control on the size of veins and the origin of conduits are important questions which remain unanswered.
6.4 Water flow and glacier temperature
This picture of the water flow needs to be reconciled with the known in situ ice temperature (Reference HarrisonHarrison, 1975[b]). The ice below approximately 6 m depth is about 0.02 deg colder than expected from the temperature lowering by the overburden pressure. It is unlikely that this depression could be caused by a large difference between vein and ice pressures; most likely it arises from dissolved impurities as assumed in Section 5.3. On the other hand, the temperature depression from impurities in the surface melt water (mostly dissolved air) is an order of magnitude smaller. If surface water does enter the veins, the impurities in it would have to be greatly concentrated; it is not clear that such concentration is possible. A large downward velocity in the veins therefore seems incompatible with the measured temperature. At the upper limit of vein size (Table II, column 2) the mean downward water velocity would be about 60 m a−1 if large numbers of veins are not blocked. This water motion should affect substantial thicknesses on a short time scale. However, the temperature changes over a year were extremely small even at the highest sensors (Reference HarrisonHarrison, 1975[b]). This suggests that the in situ vein sizes are indeed less than the upper limits which we set, or that the network is discontinuous because of bubbles or unknown effects not observable in the samples because of the relaxation. In coarse bubbly ice the mean velocity may be more than an order of magnitude smaller than in clear ice because of the blocking effects of bubbles. If it were less than several meters per year, then possibly ablation could keep pace with penetration of clean surface water even on a long time scale. It is possibly relevant that the temperature sensors were roughly 80 m down-glacier from the core sites, where the fine-grained zone of ice may have been thinner or absent. In any case, the temperature measurements indicate that flow through the veins does not flush impurities very effectively.
A second problem concerns the flow in conduits. Conduits would also tend to warm the ice, and their presence would not be consistent with the temperature if the warming time were less than the length of the melt season. For a conduit density of 1 m−2, one finds from the method described in Appendix C that the ice could be warmed to the temperature of the penetrating surface water in roughly (c/ci) × 10 d, where (c/ci) is the ratio of the effective heat capacity to that of pure ice. This ratio depends upon the vein size (Appendix C) and the presence of liquid outside the veins. It is therefore uncertain, but a value of 10 is reasonable. The warming lime is therefore 100 d. Given the large uncertainty in this lime, a conduit density of several per square meter (Section 6.2) is not necessarily incompatible with the temperature.
Acknowledgements
We would like to acknowledge the assistance given in the field by Professor E. R. Reference LaChapelleLaChapelle, David Bell, and Philip Taylor. Suzanne Cummings deserves special mention for help in the field and many hours spent making textural measurements from photographs and on samples in the cold room. The U.S. National Park Service gave permission for the field work, and the principal financial support was from the National Science Foundation under grant GA-28554. One of us (W.D.H.) also acknowledges the support of State of Alaska funds.
Appendix A Shape of air columns in veins
When gas enters a vein, its shape must satisfy the requirements of mechanical equilibrium. Qualitatively, the gas fills the central portion of the vein, excluding the liquid to fillets at the three vertices. Details of the shape can be worked out approximately by assuming that the pressure difference across the liquid-gas interface is everywhere the same. The interface between the gas-filled central part of a vein and the liquid in the fillets is cylindrical and the corresponding pressure difference is easily calculated as a function of the cross-sectional shape of the gas column. The interface at the end of a gas column is doubly curving, but the pressure difference fan be estimated using the hydraulic radius of the gas column cross-section (Baer, 1972, p. 441). Equating these two pressure differences determines the shape of the gas column cross-section. The width averaged over all viewing directions is 1.91r, where r is the root-mean-square radius. The difference between the gas and liquid pressures, the capillary pressure, is given by 2.4γLV/r where γLV is the liquid-gas surface energy.
This configuration is not in thermal equilibrium. Because the pressure in the gas is larger than that in the liquid, those parts of the vein wall exposed to the gas must be colder than those adjacent to the liquid near the vertices. Whatever the details, melting and refreezing would cause a rounding of both vein and air-column cross section. Since heat would be transported only locally, there should not be much change in total vein cross-sectional area. A limiting cross-sectional shape would be circular with the liquid excluded almost entirely, in which ease the width of the air column would be 2r. Although the shape of the end of the gas column could still be complex, it would probably be close to hemispherical, which would give capillary pressure 2γLV/r. Because of the small scale of the veins, it is likely that the local redistribution of heat occurs rapidly. If the vein liquid contains im purities, the process could he slowed, but a similar shape change would occur as long as impurities can diffuse along the vein walls.
Appendix B Adiabatic relaxation
When the vein pressure or impurity content is changed, melting or freezing will occur at the vein walls, and the latent heat will change the temperature of the surrounding ice. If the process is adiabatic and the liquid content is small, then
after equilibrium has been re-established. A is the vein cross-sectional area, T is the temperature, and the sub scripts 1 and 2 refer to values before and after the change, h, ρi and ci are respectively the Specific latent heat of fusion, the density and the specific heat capacity of pure ice. l is the vein length per unit bulk volume, and p is the bulk density of the ice. Also p ≈ pi When phase change takes place elsewhere than in the veins, ci must be replaced by an effective bulk heat capacity c’ of the ice surrounding the veins.
For the special case in which the vein water is continuously replaced by water of a given impurity content and pressure, T 2 is determined by Equation (4a) when vein curvature is neglected. If T, represents the in situ temperature, which is known, the vein area change from in situ conditions can be calculated directly from Equation (B-1).
A more complicated case occurs when the pressure change is specified, but the impurity content per unit length of vein Ci remains constant. Equations (4) then give

where p is the vein pressure, and vein curvature has been neglected. This is used to eliminate T 2 — T, in Equation (B-1) with the result

where ρ i = Cl/Al , is the initial temperature depression from impurities. This assumes that all the liquid is in the veins; otherwise c i is replaced by c 1. If the ice is line enough (I very large) equilibrium on pressure release is restored by freezing some of the relatively abundant vein water, with a small change in vein area and a temperature change approaching — β(p2—pi). In coarse ice, equilibrium is restored mainly by lowering the vein temperature by concentration of impurities, with a large change in vein area and a small temperature change.
The time for adjustment of the vein size can be roughly estimated by assuming the vein to be cylindrical and to be surrounded by an infinite medium of ice. The rate of heat flow is then calculated by standard analytical methods (Carslaw and Jaeger, 1950). Equilibrium will be reached when the total heat flow per unit length of vein reaches of pc#x2019; (T 2 — T 1)/l. The result is not very sensitive to vein size. If the liquid is confined to the veins, equilibrium is reached on the time scale of seconds to a few minutes, depending upon grain size. The assumption that the process is adiabatic, or that little heat conducts in from the surface before its completion, is therefore reasonable for locations which are more than several grain diameters into the core.
Appendix C Heat conduction in to sample
If the fractional liquid-water content of a temperate ice sample is small, and if the liquid is confined to the veins, the thermal diffusion equation is

where T is temperature, A is the vein cross-sectional area, and l is time. K = 2.1 W m−1 deg−1 is the thermal conductivity of ice, c 1 = 2.1 × 103J kg−1 is its specific heat capacity, ρi = 0,92 Mg m−3 is its density, and h = 3.34 × 105 J kg−1 is its specific latent heat, ρ is the bulk density of the sample (ρ ≈ ρi) and l is the total vein length per unit volume. lA is the total liquid content per unit volume, and the second term on the right side expresses the fact that it may change with temperature. A can be eliminated with the help of Equations (4), which give

In the special case that the impurity content per unit length of vein C l remains constant, Equations (C-1) and (C-2) give

where the effective heat capacity c is given by

.
Here θ’ = δ — — β p— T the combined temperature-lowering by impurities and curvature, and λ = ;/2(Ci’)½. An effective thermal diffusivity κ can also be defined as κ = K/pc.
In the applications considered, the temperature depression θ due to impurities is the major contribution to θ’; this gives θ ≈ θ’ and λ ≈ = 0. Since Cl = Aθ by definition from Equation (4b), the effective heat capacity may be written in the alternative forms

The first of these is the form given by Harrison (1972); lC l is identified as the temperature depression by im purities when the last of the solid phase disappears upon melting, and this single parameter determines the behavior.
If θ is constant, δA/δt is found from Equation (4a) with θ constant. Then

where θ’ — Θ is the temperature lowering due to curvature.
The numerical solution of the diffusion equation with temperature-dependent heat capacity is straight forward by a method similar to that described in Carslaw and Jaeger (1959, chapter 18). Once the temperature is found, the vein area can be found from Equation (C-2). Alternatively, the vein area can be found directly by eliminating T rather than A in Equations (C-1) and (C-2).
Appendix D Statistical analysis of blockage of veins by bubbles
Consider a unit area of some reference plane. There are n veins crossing this area. We want to know how-many of these veins can actually transport water.
Let p be the probability that any given network link represented by a segment of vein between two four-grain intersections is not blocked by any bubbles (or other type of blockage). Then it is clear that only pn of the links crossing the unit area on the plane are unblocked. In addition, some of these pn unblocked links cannot transport water because all of the paths leading to (hem from above or below (he plane are blocked. Let Q(p) be the probability that a given link crossing the plane is cut off from distant veins below the plane. In order lo transport water, the link must be connected to the vein network both above and below the reference surface. Therefore, the effective number of veins crossing the surface is
In order to estimate p, we consider the average spacing s of bubbles along veins. It is reasonable to assume that the probability of finding a single bubble touching a vein in a very short length interval is proportional to the average number of bubbles per unit length of vein (I/s) and that the probability of finding more than one bubble for such a short length interval is zero. In this case the probability of finding k bubbles on a link of length b is given by Poisson’s formula. In particular the probability of no blockage or k = o is given by

Fig. D1. Simplified topological model of the vein network.
To estimate Q(p) consider access to successively more remote groups of four-grain intersections denoted as levels 1, 2, 3, etc. in the simplified topological model of the vein network shown in Figure D-1. For the first level it is clear that Q 1 = (1—p)3. To get Q2 consider a single one of the links leading to level 1, Starting along this path, access to level 2 is blocked if this link to level 1 is blocked (probability (1 —p) or if this link is unblocked (probability p) but the triplet of veins joining it to level 2 is blocked (probability Q i. Thus Q 2 = [(1 — p) + pQ 1]3 where the third power arises because there are three possible starting paths. Successive application of this argument gives
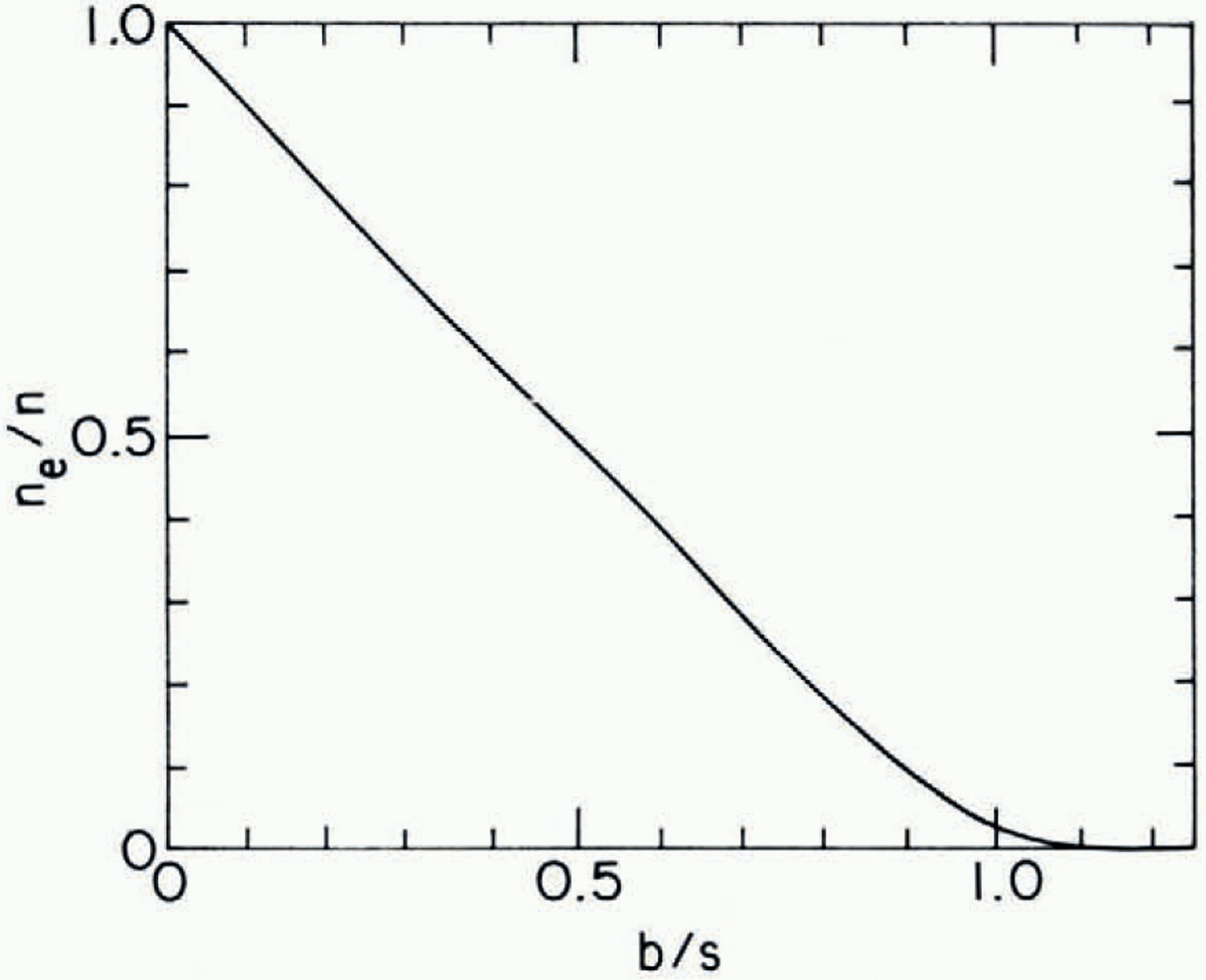
Fig. D2. Fig. D-2. Fraction of veins capable of transporting liquid across reference plane (ne/n) Versus the ratio of mean spacing of four-grain intersections (b) to the mean spacing (s) of blockages in veins.
It was found that the sequence (Qm) converges fairly rapidly, which is consistent with the obvious requirement that when p does not depend on position, local connectedness of the network implies large-scale connectedness as well. The topological model used in this calculation neglects the fact that some of the paths lead hack on themselves and that some cross back over the reference plane. Because these complications should become most important at the more distant levels of four-grain intersections and {Qm} converges fairly rapidly, the limit of the sequence is probably a reasonable estimate of Q for the real network.
Together, Equations (D-1), (D-2), and (D-3) define the relationship between n e, n, b and s. This is plotted in Figure D-2. One finds that ne/n is essentially zero (< 10−3 for b/s 1.2.















