Introduction
The idea of subglacial water-sheet floods is highly controversial, as is the connection made between floods and drumlin formation. The latter controversy reduces to two conflicting tenets: the conventional, that drumlins are streamlined forms molded by laminar ice flow, and the heretical, that drumlins are the product of turbulent water flow. The two points of view have as much in common as creationism and evolutionism.
I find the water-sheet model compelling on the basis of field evidence and (recent) theory. Perhaps the strongest field evidence supporting the fluvial model is the detailed shapes of erosional marks in rock, particularly hairpin-shaped grooves. Hairpin scours are interpreted as the product of debris-laden horseshoe-shaped vortices which form around obstacles (Reference DargahiDargahi, 1990). This idea was previously and subsequently applied to explain erosional marks on glacial beds for a wide range of scales (Reference Shaw and Sharpe.Shaw and Sharpe, 1987; Reference ShawShaw, 1988, Reference Shaw1994; Reference Sharpe and Shaw.Sharpe and Shaw, 1989; Reference Sharpe and Shaw.Shaw and others, 1989; Reference Kor, Shaw. and Sharpe.Kor and others, 1991). The initial inspiration for this model is due to Reference AllenAllen (1971, Reference AllenAllen, 1982) who verified experimentally that erosional forms such as are seen on a glacier bed are produced by separated turbulent fluid flow. Reference ShawShaw (1994) examined in detail the genesis of hairpin erosional scours. The weight of evidence supports the fluvial model. The genetic relationship between hairpin scours and certain types of erosional drumlins has been made (Reference Shaw and Sharpe.Shaw and Sharpe, 1987; Reference Sharpe and Shaw.Sharpe and Shaw, 1989; Reference ShawShaw, 1994).
Hundreds of pages of field evidence have appeared supporting water-sheet floods and their linkage to various erosional and depositional landforms. (See Reference Shaw, McCann and Ford.Shaw (1996) for a review.) Far from eliciting controversy, this evidence has simply been ignored. No detailed examination of field evidence is given here.
The theoretical underpinnings of the fluvial model are a more recent development. Reference ShoemakerShoemaker (1991) showed how large subglacial lakes, the presumed water source for at least some floods (supraglacial lakes may have been the water source for others), can form beneath ice sheets and how sub-glacial ponding reduces the ice-surface gradient. Of relevance is the recent evidence that one of the Antarctic subglacial lakes (Vostok) is much larger than previously thought, about the size of Lake Ontario (Reference Kapitsa, Ridley., Robin, Siegert. and Zotikov.Kapitsa and others, 1996). During a period of rapid deglaciation, a large supraglacial lake can create temperate ice beneath it. The possibility exists of catastrophic drainage from such a lake through temperate ice to a subglacial lake (Reference ShoemakerShoemaker, 1991). This implies that subglacial lakes beneath a deglaciating Laurentide ice sheet could have collected water much more rapidly than contemporary Antarctic subglacial lakes.
The concept and mechanics of subglacial water-sheet floods were considered by Reference ShoemakerShoemaker (1992b). Reasons were given why a flood can take the form of a sheet rather than the well-studied, and accepted, tunnel form (Reference NyeNye, 1976). Ice lift-off, with grounding only on bed highs, over a corridor hundreds of km long and at least 100 km wide causes rapid ice elongation or a surge (Reference ShoemakerShoemaker, 1992b). If this corridor reaches the terminus, an ice-sheet lobe results (Reference ShoemakerShoemaker, 1992a). Ice-sheet lobes are generally attributed to surges. For example, Reference KemmisKemmis (1991) attributes advances of the Des Moines Lobe, Iowa, U.S.A., to surges.
The criticism that water-sheet floods cannot occur because sheet flow is unstable (Reference WalderWalder, 1982, Reference WalderWalder, 1994) was refuted byReference Shoemaker and Walder.Shoemaker (1994) who showed that turbulence greatly increases the characteristic time for the viability of an “unstable” water sheet. A water sheet meters thick can exist for the order of a month or more.
Reference Shaw, Kvill. and Rains.Shaw and others (1989) calculated that a flood volume of the order of 84 000 km3 was required to form the Livingstone Lake (Saskatchewan, Canada) field of depositional drumlins. Flood volumes of this magnitude have raised much skepticism. The calculation assumes that the drumlin molds or cavities in the basal ice are melted by heat generated from water flow (Reference ShawShaw, 1983). Reference ShoemakerShoemaker (1995) showed that these cavities were more likely to be abraded by suspended sediment in highly turbulent flows. Corrasion by sand blasting is much more efficient than melting. Estimates of flood volumes cannot be made, but they could easily be at least an order of magnitude less than 84 000 km3.
Finally, corrasion of basal ice and bed erosion increase non-linearly with water-sheet velocities (Reference ShoemakerShoemaker, 1995). The inference from the fluvial model is that both depositional and erosional drumlins should tend to exist in those regions where water-sheet velocities are high, and should be absent in regions where velocities are very low.
This paper utilizes the idea that subglacial lakes affect the ice-sheet topography. The topography, in turn, has a major influence upon the subglacial hydraulic gradient during a water-sheet flood and the accompanying velocity field. By assuming the existence of subglacial lakes in major basins, such as certain of the Great Lakes, North America, it is possible to identify regions of potentially high and low water-sheet velocities near these subglacial lakes. If drumlins occur in regions of predicted high velocity and are absent from regions of predicted low velocity, the fluvial model gains credibility. If the result is contrary, the fluvial model must be rejected. Of course, if a particular basin did not contain a subglacial lake at the time of a flood, the predictions of a fluvial model based upon the assumption of a lake are inapplicable and this fact should become apparent when theory is compared with field observations.
The qualitative effect of a subglacial lake in the Lake Michigan basin is first investigated. Many prominent drumlin fields are situated nearby, and there are large areas where drumlins are absent. This suggests that a subglacial lake may have influenced a water sheet. An ice-sheet lobe is a by-product of this initial investigation. Conclusions are drawn regarding the influence of subglacial lakes in the Superior and Huron basins upon drumlin-field locations.
The situation near Lakes Ontario and Erie is considered. Here, the influence of bed topography and ice displacement is considered, as well as subglacial lakes. Consideration is given to fluvial erosion in the genesis of lake basins. Many drumlin fields occur where it is unlikely that the ice-sheet topography was unusual. Two examples are given illustrating why this need not be inconsistent with the fluvial model.
Effect of Subglacial Lakes Upon Ice-Sheet Topography
Because the basal-ice shear stress, τ b, vanishes on a sub-glacial lake, the classical result (Reference PatersonPaterson, 1994, p.240) relating τ b to ice thickness, h, and the magnitude, α, of the ice-surface gradient,
predicts a horizontal ice surface (ice lid) over the lake. However, Equation (1) need not apply in regions of diameter the order of h, or less. Reference Siegert and Ridley.Siegert and Ridley (1998) found that Antarctic subglacial lakes, with mean dimension exceeding three times the ice thickness, expressed their presence by reduced surface slopes, at least an order of magnitude less than α above neighboring grounded ice. Lakes with mean dimension no greater than the ice thickness did not significantly affect the ice-surface morphology. The ice lid over the Vostok subglacial lake has α<7 × 10−5. Accordingly, for most (but not all) purposes it is reasonable to assume α = 0 on an ice lid over a subglacial lake occupying the Lake Michigan basin, for example.
Ice topography near an idealized subglacial lake michigan, constant τ b
Figure 1 shows half of an idealized symmetric rectangular lake ABCD with AB the center line. The aspect ratio |AB|/2|BC| is five, the approximate aspect ratio of Lake Michigan. Assume that the ice-lid surface is horizontal and the specific discharge q* (m2 s−1) (flux) up-glacier from the lake is uniform and in the direction shown. The ice-sheet topography is then symmetric about ABG. Let FJ represent the position of the terminus away from the influence of the lake. This is the approximate position of the Laurentide terminus between 18 000 BP and, perhaps, 15 000 BP (Reference Dyke and Prest.Dyke and Prest, 1987), when Lake Michigan was ice-covered. It is easy to sketch the ice-sheet topography for other terminus positions once the construction is understood.
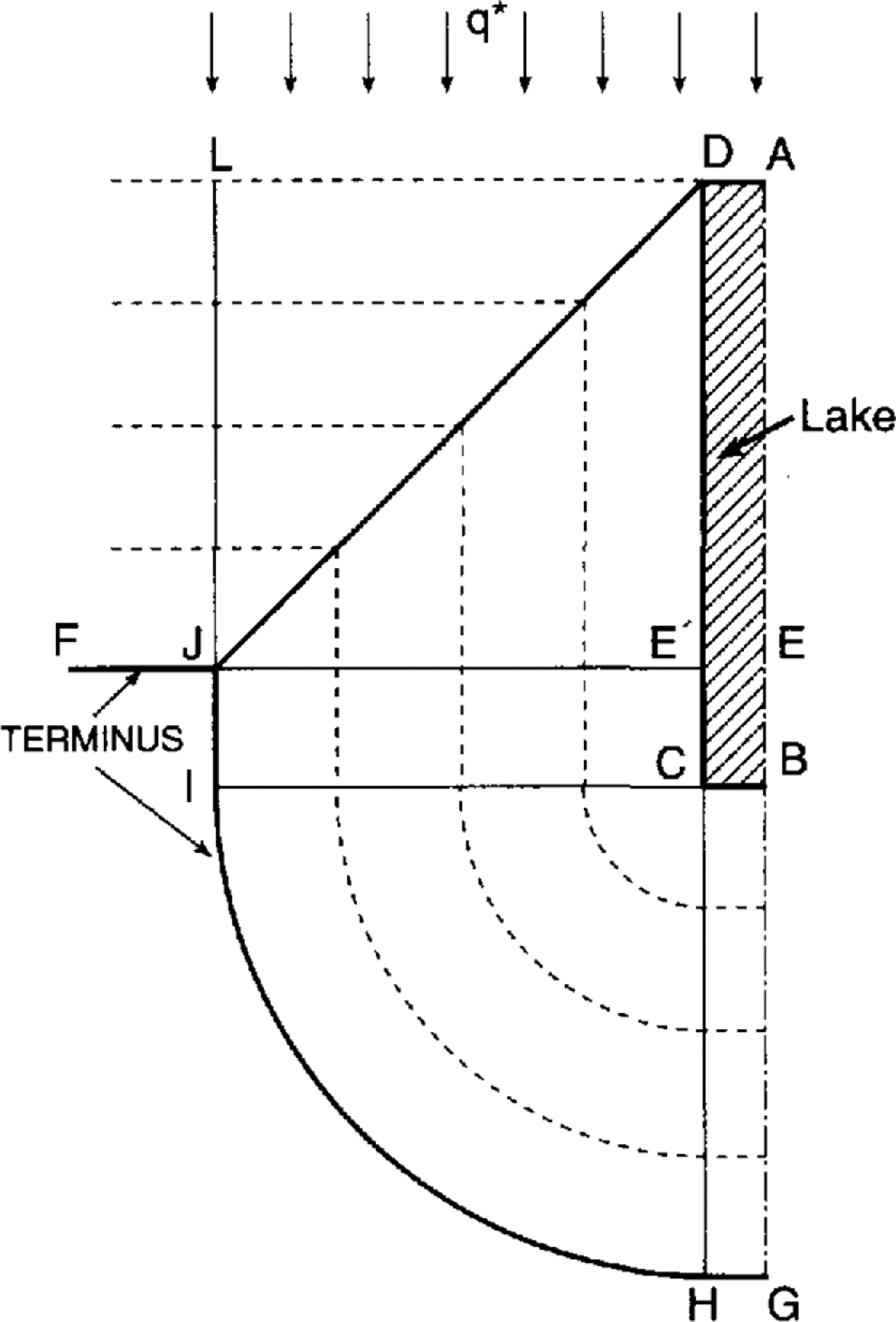
Fig. 1. Influence of idealized subglacial lake upon ice sheet (contour lines dashed) assuming constant ice-surface gradient α. FJE, terminus in absence of lake. DJ is a trough and LDABCD is at constant elevation. AG is a line of symmetry. q* is the uniform ice flux up-glacier.
If τ b is assumed constant beneath grounded ice the ice topography is unique and easily constructed. The best approach is to first assume that α is constant in Equation (1). The equally spaced dashed lines in Figure 1 are ice contour lines. LDJL and DCIJD are planes sloping downward in the direction of LJ and E’J, respectively. DJ is a straight-line trough. Region CHIC is conical and BGHCB is a plane. Lines DC and BC are ridges.
Now consider the ice topography if τ b is constant in Equation (1) and the terminus remains at FJ. Although the contour lines are not equally spaced and regions LDJL, DCIJD and BGHCB are not planes, the plan view of the solid lines in Figure 1 is unchanged. DJ is still a trough, although it steepens from D to J. α is infinite at the terminus. It is important to recognize that the ice lid is a plateau elevated hundreds of meters above point J, for example. This conventional, τ b = constant, model produces an ice-sheet lobe EGJE of length |EG| equal to the length of the lake. The lobe aspect ratio |EG|/2|EJ| depends upon the position of the terminus FJ.
In this and later examples a seal, as discussed by Reference NyeNye, 1976 and Reference ShoemakerShoemaker, 1992a), of locally elevated ice near the ice-lid grounding line is not shown around the elevated portion of ice lids. A complete seal must be present unless the subglacial lake is on the verge of catastrophic discharge.
Figure 1 is satisfactory in illustrating qualitative aspects of the ice-sheet topography, but unsatisfactory if mass conservation is considered. (In all considerations of mass conservation the arguments are qualitative and ignore accumulation and ablation.) The assumed uniform ice flux q* far up-glacier applies on line LA because, with LA at constant elevation, the presence of the lake is not felt there. The ice beneath LDJL is supplied by the ice discharge across DL. The much larger ice volume beneath DJGAD is supplied by the smaller ice discharge across AD, a contradiction. Thus, the τ b = constant assumption must be modified once mass conservation is considered.
Existence of a lobe
Figure 1 suggests that for an ice sheet that has not necessarily undergone a recent surge, an ice lobe, nevertheless, is associated with a large-aspect-ratio subglacial lake located near a terminus. However, since the ice topography is incorrect in detail, one cannot conclude yet that a lobe exists. One referee suggested that the ice lid could be depressed, rather than elevated, as is the case for some Antarctic ice streams throughout most of their length (Reference Shabtaie and Bentley.Shabtaic and Bentley, 1988, fig. 4). A surge down the subglacial Lake Michigan basin could produce a depressed ice lid (but would also produce a lobe). In all subsequent developments this surge scenario is ruled out.
Assume there is no lobe in the Michigan basin case. Make the conservative assumption that the terminus is straight as in Figure 2a. Away from the influence of the lake (e.g. along AB) the τ b = constant condition is assumed to apply. The 100 m contours correspond to τ b = 0.16 bar. The following argument strengthens as τ b increases. The value 0.16 bar is small compared to contemporary ice sheets (Reference PatersonPaterson, 1994, p. 242) but is more reasonable for warm-based ponded ice sheets (Reference ShoemakerShoemaker, 1991).

Fig. 2. Geometric argument supporting existence of lobe down-glacier from idealized subglacial Lake Michigan. 100 m con-lour lines correspond to τb = 0.16 bar away from lake influence. D, depressed ice; E, elevated ice. q* is as in Figure 1, and GC is a line of symmetry. Transition zones 25km wide assumed at lake ends (shaded). Arrows indicate ice-flow directions. (a) No lobe. Line at P chosen so that equal elevation changes of 440 m occur in both transition zones. (b) Lobe. Shift of line P up-glacier reduces α in transition zone U by factor of about four. Steep ice eliminated at L. Contours drawn assuming TT’ is a melt channel.
Transition zones of steep ice connect the nearly horizontal ice lid to grounded ice where the topography is unaffected by the presence of the subglacial lake. Generous transition-zone widths of 25 km are assumed at both U and L in Figure 2a. Transition widths are generally <14 km in shear zones adjoining Antarctic ice streams and zones adjoining grounding lines (Reference Shabtaie and Bentley.Shabtaic and Bentley, 1988).
Objections arise from this no-lobe assumption. (1) The total change in elevation in the transition zone, or zones, is about 880 m. This is a large change to be accommodated in 50 km or less. If τ b > 0.16 bar this objection is magnified. (2) Enhanced flux should accompany the steep ice at L. This, in turn, should produce a lobe. If this objection is removed by assuming that the entire ice lid is depressed, as has been suggested, then ice flows into the ice lid throughout its length. Consequently the ice discharge out of the lid at L is very-large, which contradicts both the no-lobe assumption and the absence of steep ice at L. (3) A subglacial lake is an ice conduit which offers no subglacial resistance to ice movement. It is difficult to see how a lobe cannot result from a large-aspect-ratio ice conduit residing near the terminus as in Figure 2a. (4) Many Laurentide lobes were aligned with Great Lakes basins, including the Erie–Ontario, Michigan, Superior and Huron lobes (Reference Dyke and Prest.Dyke and Prest, 1987). It could be argued that the James and Des Moines Lobes were associated with the numerous lake basins of Minnesota and southern Manitoba, including Lake Winnipeg.
These objections are removed in Figure 2b where point P, the boundary between depressed and elevated ice, is shifted towards U. This reduces the elevation change in the transition zone at U, the more so the closer P is to U. Steep ice near L is eliminated. The main ice flow and ice flowing from the ice lid across TL intersect at TT′. This could be a pressure ridge but in a period of deglaciation should be a melt-channel trough. This is reflected in the upward-turning contours at 2′ and 3′. Upward turning at 1′, 2′ and 3′ is also increased by the fact that the ice discharge across BH (not HG) feeds region TIAT′T. The right portion of this region is shielded and receives a reduced flux. TT′ is tangent to the ice lid at T′ because the ice flux from the lid vanishes there. Since the flux from the lid increases from T to L, the trough curves as shown. The shape of TT′ is only suggestive and the upward curvature may not extend to T′.
The location of P is determined by ice balance. The ice discharge on BH feeds the ice volume V1 beneath TIAT′T. The ice discharge on HG feeds V2: the ice beneath TT′CLT plus the ice beneath region E. As P moves towards U, H moves towards G, so the discharge feeding V2 decreases. The effect upon V1 is the opposite. Point P resides where the ice discharges across BH and HG are in proper proportion to V1 and V2, respectively, depending upon how close the ice sheet is to steady state. The remainder of this development does not rely upon the existence of an ice lobe, although Figure 3 is drawn assuming a lobe.

Fig. 3. Contours near idealized Lake Michigan–Green Bay subglacial lake. Ice discharge across HG feeds ice lids and lobes. τ b = 0.16 bar along AB and CF. Contours drawn assuming trough TT′ is a melt channel.
Ice topography near a subglacial lake michigan-green bay, non-constant τ b
Figure 3 shows the ice topography near a subglacial lake occupying idealized Lake Michigan and Green Bay basins. Symmetry is assumed about line CC. The outline of the contemporary lakes appears in Figure 5. It is assumed that the entire basin complex contains a lake. The consequences of this assumption are compared later with field evidence.
The terminus AT′ corresponds to Figure 1. Contour 1-1′ is at the elevation of the ice lids. This choice of point P appears to render reasonable mass balance. τ b is set equal to 0.16 bar on AB and CF, with the contour spacings on these lines computed from Equation (1). As before, trough TT′ lies within a supraglacier melt channel and marks the boundary of intersecting ice-flow fields. Segment Tt of the trough is a line which lies closer to the Green Bay boundary than to Lake Michigan because the ice flux from the larger Michigan lid dominates the ice flux from the smaller lid. The curve of segment tT′ reflects the increasing ice flux from the Michigan ice lid as the relief increases towards D. A minor trough issuing from point 1′ is not shown.
Once τ b, P and TT′ are chosen, the qualitative character of Figure 3 is determined. Details which are indeterminate include the shape of the contours near the trough, which depends upon the extent of melting by surface runoff and the effect of ice flow from the Green Bay ice lid upon the Green Bay “lobe”. This Green Bay discharge can also influence the shape of the terminus AT′. Note that α is relatively large on the flanks of the ice lids. As drawn, τ b achieves values up to 0.8 bar.
Regions of high and low velocity
Figure 3 can be used to determine regions of high and low velocities for a water sheet passing beneath the ice profile. Assuming uniform flow along a flowline, which is adequate here, V satisfies
(Reference ShoemakerShoemaker, 1995). Here, n is Manning’s number (SI), q (m2 s−1) is the specific water discharge (flux) and m, in the terminology of open-channel flow, is a head gradient given by

where ρ w is water density, s is downstream distance along a flowline, b is bed height above a horizontal datum and y is the water-sheet thickness. Assume that db/ds = 0 except on the banks of the subglacial lakes. Take ρ/ρ w = 0.9.
It is convenient to utilize the ice-surface slope in the direction of flow, α s. Then, Equation (3) can be written approximately as
The flow field for the subglacial water sheet is now approximately the same, and would be identical if ρ/ρ w = 1, as the flow field for a water sheet travelling on top of a fully grounded ice sheet which has supraglacial basins, averaging perhaps 100 m in depth, identical to and situated above the original subglacial lake basins. An open-channel supraglacial water-sheet flood over this fictitious ice topography can be visualized more easily than the actual subglacial flood. However, because of ice stiffness, under conditions of rapidly varying flow a subglacial water sheet can, over short distances, behave as a confined flow, with pressure more or less than the overburden pressure. For this special circumstance Equation (2) does not apply. The supraglacial flood analogy also fails locally.
There are several notable features of this fictitious supraglacial flood which is similar to a river flood, the difference being that the water which escapes laterally across the banks of the ice basins flows rapidly down the flanks of the elevated ice lid where m in Equation (2) is large (Fig. 3). (1) There is convergent flow into the depressed ice-lid region near JU in Figure 3 from the ice cirque which has a relief in excess of 200m. Deep water in this depressed region pushes the flood southward (m ≈ dy/ds there). Although q is high in the lake basins, V is low because of the large water depth. Note that a head gradient of 10−4 along either basin axis produces a flux which is much larger than the flux produced beneath previously grounded ice by a typical head gradient of 10−3 and a typical water-sheet thickness of 30 m. (2) There is strong convergent flow near the trough TT′ (Fig. 3) where q is very high. (3) V can be high on the banks of the supraglacial ice basin where m values are large. (4) A region of divergent flow and low V exists in DECFD. These features are sketched in Figure 4.
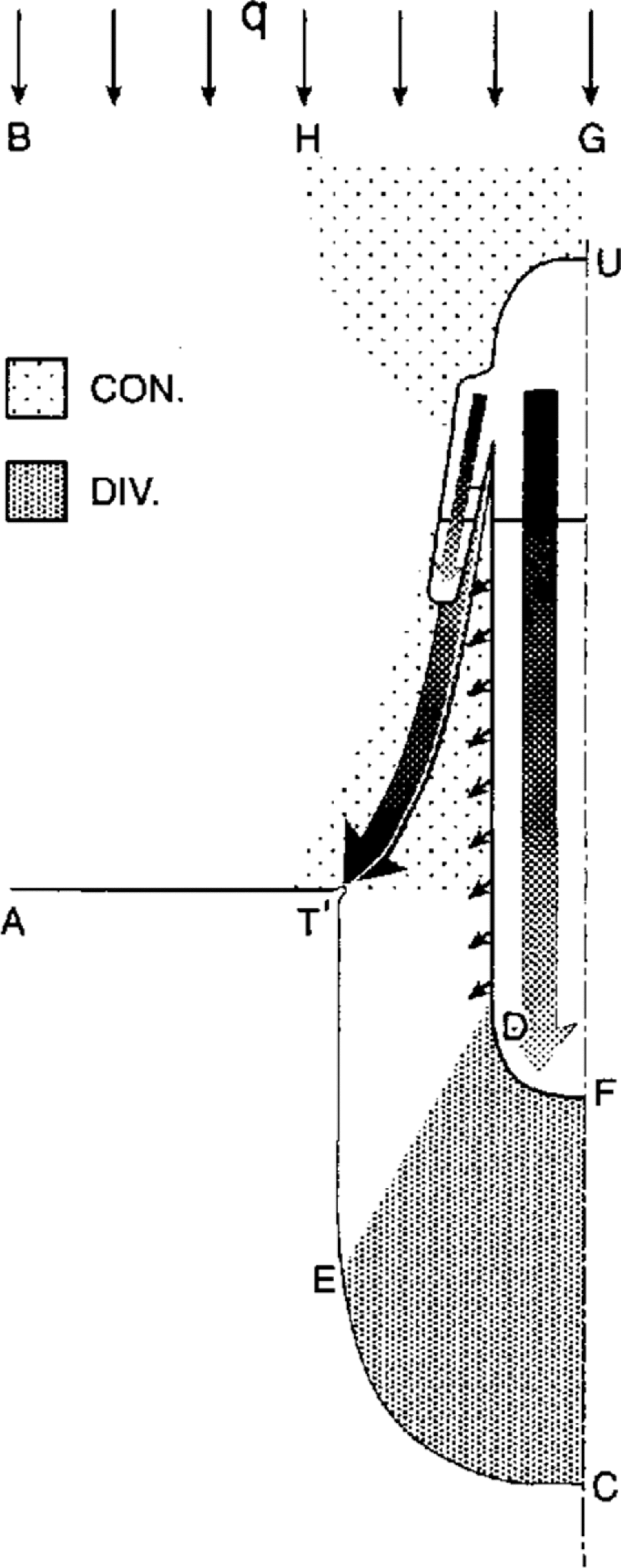
Fig. 4. Regions of high and low water-sheet V corresponding to Figure 3. Large arrows show major flow paths. Shading indicates flux intensity. Small arrows show possible large V under ice-lid ramps. Convergent and divergent flow regions shaded.
The pronounced change in flow direction of the fictitious supraglacial flood, and corresponding subglacial flood, near the trough is important. Water exits the supraglacial ice basin roughly perpendicular to the basin margin. Here the dominant term in Equation (3) is dh/ds. As this water approaches the trough the flow direction changes rapidly until it is roughly aligned with the trough. The controlling term in Equation (3) in this turning region is –dy/ds. That is, shallow water travelling down the steep flanks of the ice basin is forced to turn by deep water in the ice trough.
In this interpretation it has been assumed that the ice sheet lifts off its bed but undergoes no displacement down-stream. Ice displacements, which can greatly affect the velocity field (Reference ShoemakerShoemaker, 1995), are considered later in connection with drumlins near Lake Ontario.
The extent of a subglacial lake
At the time of a water-sheet flood the extent of a subglacial lake in any basin is unknown. A subglacial lake grows until, normally, it discharges some or most of its volume by an outburst flood (Reference ShoemakerShoemaker, 1991). One cannot determine theoretically the state of any particular subglacial lake within its filling–discharge cycle at the time of a subglacial water-sheet flood. Because the size of a horizontal ice lid is determined by the size of the subglacial lake, the ice-sheet topography near subglacial basins is theoretically indeterminate.
Two additional unknowns can limit the maximum extent of a subglacial lake, particularly in a large basin. If local isostatic equilibrium is attained, ice depresses bedrock by about one-third the ice thickness. However, the time duration of an ice lid over a subglacial lake is almost certainly too short to achieve isostatic equilibrium. Third, there must be a small non-zero surface slope, α, on the ice lid because the lid cannot adjust instantaneously to the input of ice in the depressed region and loss of ice in the elevated region. α could easily be greater than 7 × 10−5, the value for the ice surface over the large Vostok subglacial lake. Corresponding to a surface slope α, the base of the ice lid has an adverse slope of ≈ 11α (Reference ShoemakerShoemaker, 1991). The isostatic effect tends to limit the down-glacier extent of a subglacial Lake Michigan. The ice-lid subsurface gradient tends to limit the up-glacier extent. Since the two effects tend to cancel, it is conceivable that the entire Lake Michigan basin contained a lake at the time of a water-sheet flood.
In time, we may learn how to determine the size of paleo-subglacial lakes from field evidence. Sediment is deposited where a water-sheet flood encounters the deep water of a subglacial lake. A moraine is formed. There are numerous candidates for such moraines near the northern boundaries of the contemporary Great Lakes, including the Oak Ridges moraine north of Lake Ontario. This contains large masses of glaciofluvial and glaciolacustrine deposits (Reference DuckworthDuckworth, 1979). Note that such moraines may exist beneath contemporary lakes.
Comparison with field evidence and some implications
Erosion increases with V to a high power (Reference ShoemakerShoemaker, 1995). Drumlins should therefore tend to occur in the convergent flow regions (Fig. 4) as well as on the bed beneath the steep ice-lid flanks (Fig. 3). Drumlins should be absent from the divergent flow region.
Figure 5 illustrates drumlin fields near several of the Great Lakes. Drumlin swarms tend to congregate near the flanks of Lakes Superior, Huron, Michigan, Green Bay and Grand Traverse Bay (T). The emphasis here is on the drumlins in insert a. A moraine, I, interpreted as an interlobate moraine (Reference AldenAlden, 1918), appears at the approximate position of TT′ in Figure 3. It is striking how this moraine marks the boundary between drumlin fields of different orientations. This is consistent with the flow field of Figure 4 if the drumlins to the east of the moraine are assumed to be formed by sheet flow beneath the steep ice above the flank of subglacial Lake Michigan and the drumlins to the west of the moraine are the product of the main sheet flow, with this flow turning towards the trough TT′. The fluvial model suggests that this moraine may not be an interlobate moraine but rather marks the location of a supraglacial trough. The moraine could be composed of sediment deposited beneath the trough during the waning phase of a water-sheet flood when the major flood routes, carrying the last of the flood, became sediment traps.
A similar situation occurs in insert b, although the interpretation is less clear. M is part of a longer moraine (Flint and others, 1959). However, the similarity between drumlin orientations at M and I suggests that at least part of M reflects the sediment deposited beneath a supraglacial trough. Because the extent of a subglacial lake in the Superior basin, if one existed, is unknown, it could have extended outside the boundary of the present lake. A supraglacial trough could issue from any point above the unknown sub-glacial lake boundary.
The southwestern part of moraine M appears, at first glance, to mark the boundary between two flow fields, one on the north side of the lake and the other on the south side. These flow fields apparently converge on the lee side of the lake. This interpretation is probably incorrect. As previously shown, the flow issuing from the lee side of a sub-glacial lake diverges and this divergent flow pattern is evident in the second flow field.
Figure 6 sketches part of a possible subglacial lake and corresponding ice-surface profiles which are largely consistent with the drumlin orientations of insert b. The ice-surface contours are obtained by applying the principle that contours and drumlin orientations are roughly perpendicular. TT′ is a segment of a possible supraglacial trough. The subglacial lake is chosen to include LS plus a portion, S, of the contemporary dry lake basin.
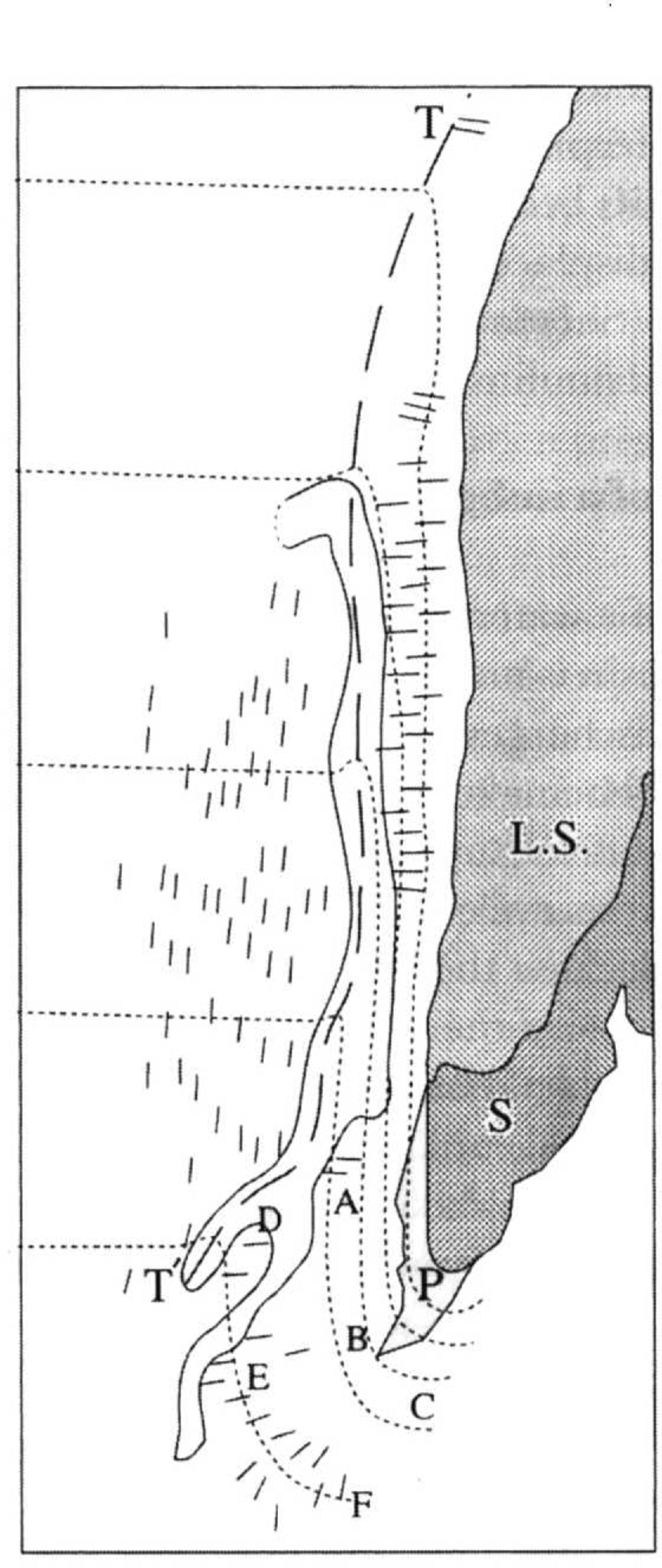
Fig. 6. Ice-sheet profiles near elevated ice lid over part of Lake Superior. LS, contemporary Lake Superior; S+P, proglacial lake (Flint and others, 1959); LS+S, subglacial lake and we lid. Short line segments: drumlin orientations from Figure 5.
By the construction of Figure 6 the ice ramp to the right of the trough is very steep. This is consistent with the fact that the width of the ice lid tapers strongly towards its lee end. The ice flux from the lid would then diminish towards the lee end. This effect pulls the trough TT′ towards the ice lid and increases α on the ramp.
An important difference between this case and the Lake Michigan case of Figure 4 is that the Superior basin narrows downstream, producing convergent basin flow. The flux issuing at the basin terminus could be many times greater than the corresponding flux issuing from the broad Michigan terminus. The discharge should also be greater because of the much greater basin size at the stoss end.
Why do no drumlins occur between are ABC and the subglacial lake (Fig. 6)? The flux should be larger there than near are DEF where drumlins do occur. There are two possible explanations. First, the subglacial lake and ice lid could extend beyond are ABC. Second, there is field evidence suggesting that erosional drumlins are the result of an intermediate state of erosion. In broad regions containing both drumlinized and non-drumlinized zones, frequently the most highly eroded areas are not drumlinized (personal communication from J. Shaw). Evidently, very intensive erosion can erase drumlins. In Finland, many cross-cutting fan-shaped flows appear to have erased all drumlins in their paths, while eroding new drumlins (Reference PunkariPunkari, 1982).
Partial explanations are offered concerning the other drumlin fields in Figure 5. If upper Lake Michigan and upper Lake Huron had depressed ice lids, subglacial water flow would converge on these regions from up-glacier, and the discharge from these regions would diverge. Fields 1 and 2 could then be the result of discharge from these depressed regions, with flow fields diverging in the gap between Lakes Michigan and Huron. (Note the divergent pattern of fields 1 and 2.) The drumlins of fields 3 and 4 are nearly parallel. The corresponding sheet flows appear to issue from the Lake Superior basin. There is no ready explanation as to why these drumlin fields should be precisely where they are.
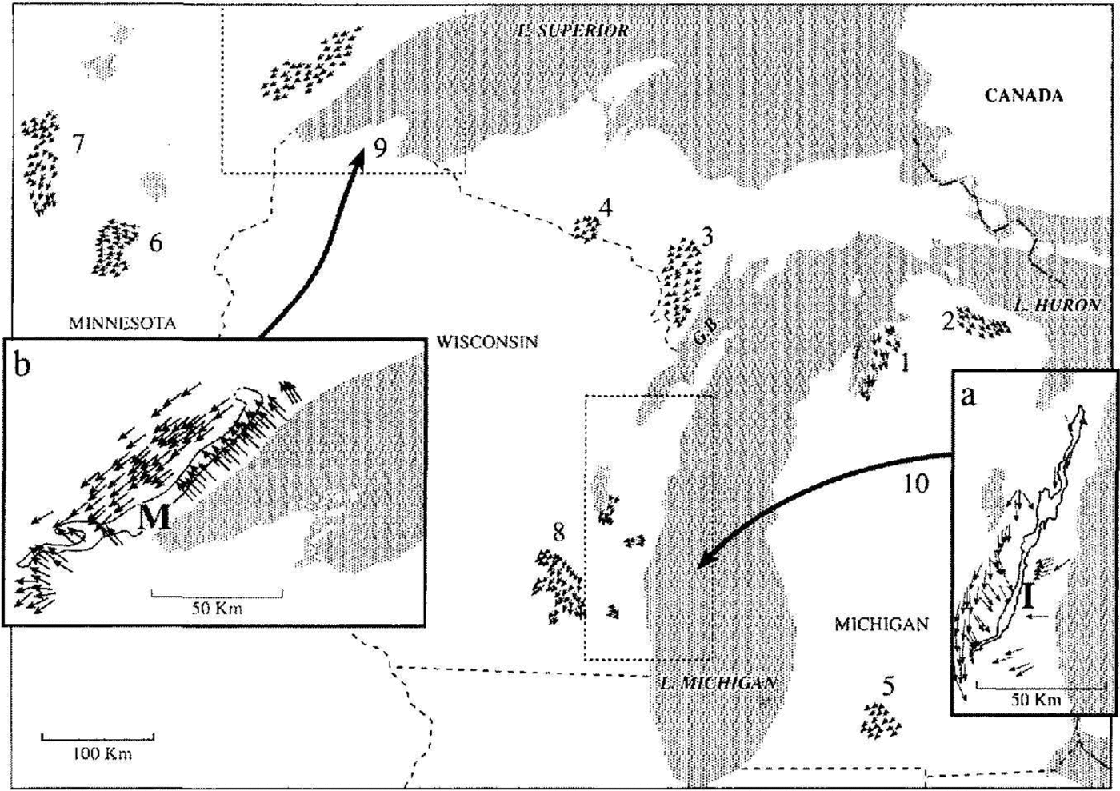
Fig. 5. Prominent drumlin fields in north-central U.S.A. after Reference Mills, Menzies and Rose.Mills (1987). Shaded areas are contemporary lakes. Arrows indicate drumlin orientations and extent of fields, from Reference Flint, Colton., Goldthwait. and Willman.Flint and others (1959). Inserts (a) and (b): details of boxed regions with I an “interlobate” moraine and M a moraine. T, Grand Traverse Bay.
Fields 6 and 7 correspond to two sheet flows which converge strongly. This could be the result of an ice-marginal effect, flow convergence towards a supraglacial drainage channel or trough. Erosional processes in fields 5–8 may also have benefited from another ice-marginal effect. Water-sheet velocities increase towards the margin, particularly if the margin is grounded, because of the increase in α.
It is important to question the model’s ability to predict where drumlins should not occur. There are no drumlins in the divergent-flow region of Figure 4 where V is predicted to be low. Drumlins are also absent in large regions surrounding fields 9 and 10 (Fig. 5), where divergent flows are predicted. It is possible to find many other regions with predicted low V where drumlins are absent. Note, however, that drumlins do occur in the lee of Lakes Erie and Ontario. This will be examined later.
The results are largely consistent with the fluvial model and with the assumption that the basins of lakes Michigan, Superior and Huron contained subglacial lakes, with accompanying ice lids, at the time of water-sheet floods. The extent of these lakes is unknown, but the Michigan basin may have been nearly full. These conclusions follow from the decent fit between predicted and actual drumlin-field locations and orientations. The absence of drumlins in regions of predicted low V (Fig. 4) adds weight.
Effect of Bed Topography: Lakes Ontario and Erie
Major drumlin fields occur near the boundaries of Lake Ontario (Fig. 7). Drumlins also occur in the lee of the eastern shore of Lake Erie (Fig. 7), and “glacial” grooves are known on all the flat-lying limestone islands in western Lake Erie. The largest megagrooves are on Kelleys Island (Fig. 7) (Reference GoldthwaitGoldthwait, 1979). These grooves may be the product of fluvial erosion, evidence of a high-energy flood through the Lake Erie basin. There is no accepted model for their genesis, although erosion by ice or ice-slurry action is generally assumed (Reference GoldthwaitGoldthwait, 1979).

Fig. 7. Drumlin orientations near Lakes Ontario and Erie, from Reference Flint, Colton., Goldthwait. and Willman.Flint and others (1959), Reference Prest, Grant. and Rampton.Prest and others (1968) and Reference Karrow and FultonKarrow (1989). Contour lines based
upon subglacial lakes in basins. Contours in northeast corner based upon
surge along St Lawrence valley into Lake Ontario. Escarpments: 1.
Ordovician; 2. Niagara; 3. Erie. β values for transects (see
Fig. 8): 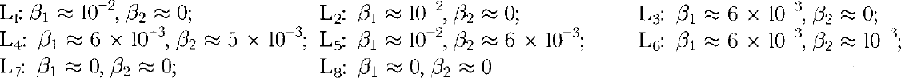 A, Ashtabula; B, Buffalo;
C, Cleveland; K, Kelleys Island; Ki, Kingston; L, Lorain; Lo, Lockport;
O, Oswego; R, Rochester; S, Sandusky; SL, Saint Lawrence valley; To,
Toledo.
A, Ashtabula; B, Buffalo;
C, Cleveland; K, Kelleys Island; Ki, Kingston; L, Lorain; Lo, Lockport;
O, Oswego; R, Rochester; S, Sandusky; SL, Saint Lawrence valley; To,
Toledo.
There are several related questions to answer. (1) Why do drumlin orientations near Lake Ontario vary by nearly 180°? (2) Why are these drumlins largely confined to belts about 60 km wide (but up to 70km) bounding the north and south shores, with the most prominent drumlins confined to a region up to 30 km deep on a plateau to the southeast (Fig. 7)? (3) Why do the Finger Lakes of northern New York state occur near the southern extremities of the southern drumlin belt (Fig. 7)? (4) Can any conclusions be drawn related to Lake Erie, in particular in the genesis of the megagrooves? Most of these questions can be answered fairly satisfactorily if both the Ontario and Erie basins contained subglacial lakes at the time of a water-sheet flood. This condition is assumed in the following.
Ice-elevation contours to the north of Lake Ontario are based upon two assumptions: (1) The subglacial lakes are identical in plan form to the contemporary lakes. (2) The contours relate to the ice-surface profile before ice displacements during the flood, with one exception discussed below. Therefore, with this exception, contours are generally parallel to the lake boundary. Previous comments still apply that the extent of a subglacial lake is unknown.
Ice displacements will be shown to be very important. In Figure 7 the contours near Kingston apply to the ice surface after an assumed surge along the upper reach of the Saint Lawrence Valley into Lake Ontario. With the ice sheet presumably anchored to the Ordovician Escarpment this surge would be confined to east of the escarpment. The surge could have preceded the flood. Figure 7 shows that the highly aberrant drumlin orientations down-glacier from Kingston are roughly orthogonal to surge-induced contour lines. A similar procedure can be used to achieve orthogonality throughout Figure 7, but is highly artificial and is a circular argument in support of the model.
What would the situation be in the absence of subglacial lakes? The effect of a subglacial dry basin upon subglacial sheet flow is the same as the effect of a similar basin, with a depth reduction of nine-tenths, upon open-channel flow. It is likely that open-channel flow into a basin the shape of Lake Ontario and averaging about 10 m in depth would have little effect upon flow directions as compared to the wide variation of drumlin orientations in Figure 7.
Ice displacements, damming and lake levels
To the south of Lake Ontario the situation is complex. Reference Shaw and Gilbert.Shaw and Gilbert (1990) attempted to explain the extraordinary divergence of drumlin orientations by postulating two flood events: the Algonquin which was nominally to the south, and a later Ontarian event which was southwestward along the Ontario and Erie basins. In Figure 7, these events are shown as phases 1 and 11 of a single water-sheet flood. The switch in directions of the flood will be tied to ice displacements and consequent flood damming.
The analysis rests upon some facts. If an ice sheet is not displaced down-glacier, a subglacial water sheet of at least depth d can climb over a bed obstacle of height 10d. However, if the ice sheet is displaced down-glacier the grounded-ice topography can be radically altered (Reference ShoemakerShoemaker, 1995). Now, the water depth required to climb the bed obstacle of height 10d can be less or more than d, depending upon the new grounded-ice profile. Regardless of whether there is ice displacement, to lift ice over an obstacle of height d, without grounding, requires that the water be sufficiently deep to float the ice over the obstacle. To do this, normally the head must be increased at the obstacle by damming and water back-up. There is also the possibility of dragging or pushing ice over an obstacle.
Now consider what happens when a southward-flowing water-sheet flood discharges from a subglacial Lake Ontario. To the west the steep Niagara escarpment (Fig. 7) acts as a dam, more exactly as a sluice gate. There is the possibility that the ice is pinned at the scarp where the relief exceeds 100 m in places. Pinning could be preceded by a small ice displacement which moves thicker ice onto the escarpment. Regardless, the ice is pressed against the escarpment. This action temporarily reduces q severely.
It is important to understand how damming at the Niagara scarp affects the water level in front of the dam and in other parts of the basin. Is the water level raised to such a height that ice can be floated over the escarpment? This question is easily answered. It is sufficient and conservative to assume that in the basin the only contribution to m in Equation (3) is from the term dy/ds (neglect the ice and bed slopes). One example is sufficient to clarify the problem. Assume that q = 300 m2 s−1, a moderate flood peak value (Reference ShoemakerShoemaker, 1995). Use continuity
along with Equation (2). Assume that m = 0.001 well upstream from the basin under previously grounded ice and solve for y upstream. This gives y ≈ 36 m. Taking 85 m as the average depth of contemporary Lake Ontario, assume that the water depth in the basin is 121 m, corresponding to q = 300 m2 s−1. Using Equations (2) and (4) again gives m ≈ 1.7 × 10−5 in the basin. Since Lake Ontario is about 70 km wide the estimated change in head across the basin is about 1.2 m. The same flux carried the entire 300 km length of the basin produces a head drop of about 5 m. These values are so small they justify the crude analysis.
The conclusions are: (1) Even with damming at the Niagara scarp the water depth
is nearly uniform in the basin. (2) Because the escarpment relief exceeds 100 m
in places, pinning is very likely unless outlet damming is very extensive
elsewhere. An exception to pinning might occur east of Lockport (Fig. 7), where the escarpment is less steep
and its relief decreases eastward. (3) Extensive damming increases the flux at
undammed basin outlets. From Equations
(2) and (4),
![]() so that
increases in water-sheet thicknesses and lake levels occur. Corresponding to a
scenario to be discussed later, output q values could
conceivably increase by, say, a factor often relative to input values with a
corresponding increase in y above usual values by a factor of
about four. In this extreme circumstance ice could be floated over the Niagara
Escarpment.
so that
increases in water-sheet thicknesses and lake levels occur. Corresponding to a
scenario to be discussed later, output q values could
conceivably increase by, say, a factor often relative to input values with a
corresponding increase in y above usual values by a factor of
about four. In this extreme circumstance ice could be floated over the Niagara
Escarpment.
Water escapes under the sluice gate but it takes time to melt or erode channels (Reference NyeNye, 1976; Reference ShoemakerShoemaker, 1992b), a process which is required to enlarge the effective sluice-gate opening. Reference Gilbert and Shaw.Gilbert and Reference ShawShaw (1994) reported on channels cut through the southeastern arm of the Ordovician limestone escarpment north of Lake Ontario (Fig. 7) where the escarpment relief is about 45 m. My interpretation is that these channels formed over several glaciations in response to the situation just described. Channels were incised in the rock, and likely melted into the ice, in response to water-sheet floods being dammed at the escarpment. The assumption that a surge up the St Lawrence Valley resulted in the displaced ice topography of Figure 7, near Kingston, was partially based upon ice-sheet pinning at this escarpment.
The damming at the Niagara escarpment causes a discharge from west to cast in the lake basin. This discharge goes over the Allegheny scarp where, initially, in the absence of major ice displacement, there is sheet flow with little or no grounding. The connection between displacement and grounding is discussed below. Thus, during at least the early stage of the phase I flood, q over the Allegheny scarp is much greater than q over the Niagara scarp. The drumlins east of Rochester are likely to have formed at this time because, as will be shown, the flood was dammed at the Allegheny scarp during flood phase II and the late stage of phase I. Note the orthogonality of drumlin orientations and contour lines in this region, and the general non-orthogonality to the west of Rochester (Fig. 7).
Major ice displacement accompanies large subglacial water-sheet floods unless the ice is sufficiently grounded (Reference ShoemakerShoemaker, 1992a, b). With the removal of shear stress over most of the bed, ice-sheet equilibrium is accomplished by grounding off the margins of the water sheet and grounding at bed obstacles, such as major humps or escarpments. Major ice-sheet advances, such as a 100 km advance of the Quinn Lake lobe over a width of 140 km (Reference DredgeDredge, 1983), are more understandable if they are the product of water-sheet floods rather than the normal surge phenomenon associated with valley glaciers.
In addition to the ice displacement assumed near Kingston in Figure 7, major ice displacements probably occurred east of the Niagara Escarpment during the phase I flood. Displacement magnitudes there are limited by four factors. First, as displacement proceeds, thin ice is replaced by thicker ice. From Figure 8 with bed slope β 1 > 0 over distance d, an ice summit of relief d β 1, relative to the ice-lid surface, develops over displacement d. If bed slope β 2 > 0 the ice-summit relief increases with additional displacement. β 1 and β 2 values are given for some transects in Figure 7. As the ice thickness increases, y and q values decrease. Provided discharge from the basin is possible by other routes, so that the basin head is not greatly increased by pervasive damming, q is effectively reduced to zero after sufficient ice displacement. As before, rather than consider the effect of displaced ice upon a subglacial water sheet, it is easier to visualize the flood by imagining an equivalent fictitious open-channel flood on top of the grounded-ice profiles of Figure 8. To make the supraglacial flood strictly equivalent, ice thicknesses must be reduced by 10%. Within this context it is more descriptive to speak of an ice dam. It is clear that if the dam height continues to increase, eventually the equivalent supraglacial flood, of limited depth, cannot overtop the ice dam.

Fig. 8. Effect of displacement upon the grounded–ice profile. EFO is subglacial lake transferred to fictitious supraglacial basin. Profile Oabc is profile after displacement d. Primed and double-primed profiles correspond to displacements 2d and 3d, respectively.
Second, bed or ice humps down-glacier from Lake Ontario may produce grounding (Fig. 9). Ice can be pushed over grounded patches, but as grounding increases, the sliding velocity slows until sliding is effectively eliminated. The northern boundary of very hilly terrain is shown in Figure 7. At 14 ka BP the ice-sheet terminus south of Lake Ontario is shown by Reference PrestPrest (1969) to coincide roughly with this boundary. At this time, large ice-sheet displacements east of the Niagara Escarpment may have been possible. Ice displacement likely produces localized grounding, even on a bed of low relief, during all but the peak-discharge flood phase. Figure 9 illustrates how even small displacements introduce bed and ice roughness. Reference Rains, Shaw., Skoye., Sjogren. and Kvill.Rains and others (1993) discussed field evidence which indicates scour zones (zones of intense sheet flow) separated by zones of lesser or little erosion, interpreted as grounding zones.
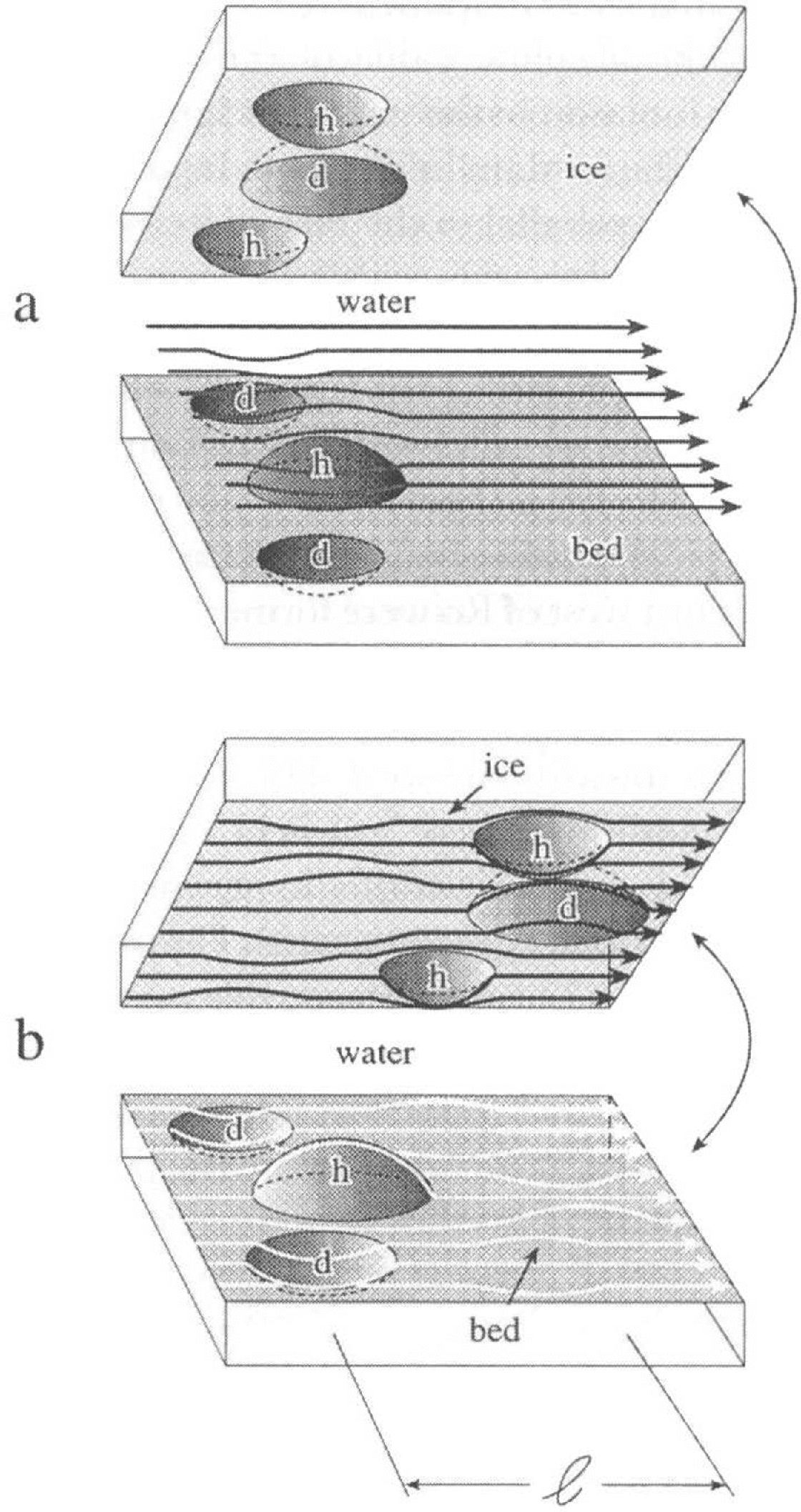
Fig. 9. Depressions d and humps h. (a) No ice displacement. Water-sheet thickness uniform and flowlines nearly planar. (b) Ice displaced distance l. Sheet is thin at h and thick at d. Flow diverges around h and converges towards d. Grounding can occur at h.
Third, grounding near the terminus induces a deviatoric compressive stress,
![]() , in the ice
sheet. Thus, in Figure 8 the thickness of
the ice dam is increased by compressive strain. By calculation, this effect can
be significant if, for example, the effective ice temperature is 10°C, or
warmer,
, in the ice
sheet. Thus, in Figure 8 the thickness of
the ice dam is increased by compressive strain. By calculation, this effect can
be significant if, for example, the effective ice temperature is 10°C, or
warmer, ![]() is at least 10
bar and the duration of the water-sheet flood is at least 20 days. Corresponding
to this range of values, the ice thickness increases by at least 28
%.
is at least 10
bar and the duration of the water-sheet flood is at least 20 days. Corresponding
to this range of values, the ice thickness increases by at least 28
%.
The critical final factor which determines displacement magnitudes is the combination of the location of the sub-glacial lake margin and the water-sheet thickness. If the lake margin in Figure 8 extends outside contemporary Lake Ontario, length d is reduced and this decreases the range of ice-dam relief values. If the entire lake basin were covered by an ice lid the dam relief at point a in Figure 8 would be eliminated. As remarked earlier, the lake size is unknown. Similarly the water-sheet thickness cannot be evaluated accurately, particularly beneath transition-zone ice where α is not well known. Calculations for a range of α from 10−3 to 10−2 indicate a y-value range of 14–28 m corresponding to q = 200 m2 s−1, and 0f 27–54 m at q = 600 m2 s−1. q values could exceed this range, particularly if exits were blocked by ice dams.
Drumlin orientations west of rochester
Between Rochester (Ro) and Lockport (Lo) to the west, drumlin orientations are not orthogonal to contours which are parallel to the boundary of Lake Ontario (Fig. 7). However, if flood-induced ice displacements are assumed to have preceded drumlin formation, the topography of displaced ice can be shown to be broadly consistent with drumlin orientations. The argument rests upon the hypothesis that these drumlins were created in a time-transgressive manner from cast to west as an ice dam developed over the Allegheny scarp and progressively narrowed the gap through which the flood passed between Lockport and a moving eastern boundary.
From Figure 7 it is reasonable to expect that displacements would be relatively large north of the Finger Lakes and diminish to the west, because the northern boundary of hilly terrain is most distant from Lake Ontario in the Finger Lakes region. This distance narrows to the west where the effect of pinning at the Niagara Escarpment is felt.
Figure 10 outlines the idea in a simplified version. Idealized displacement profiles between Lo and Ro are shown at times t i, i = 1,..., 5. Because flood discharge and water-sheet thicknesses increase until the flood reaches the termination phase (Reference ShoemakerShoemaker, 1992a), maximum possible displacements, before grounding terminates sliding, also increase with time. These maximum displacements are denoted by d i and, for simplicity, are assumed to be constant independent of position X. At t 3, for example, the displacement is maximum between g3 and Ro. In the gap between Lo and g3 the displacement is assumed to vary linearly with X. Assume that the flux and discharge are negligible on g3<X<Ro.

Fig. 10. Idealized ice displacements, d, between Lockport (Lo) and Rochester (Ro) at various times ti.
On transects to the west of Ro, dam relief normally increases with ice displacement, as for example along transect L4 (Figs 7 and 8). This is incorporated into the interpretation of Figure 10. Thus, the linearly varying ice displacement in the gap, gi<X<Ro generates a component of ice-surface slope parallel to the lake boundary. For simplicity, assume that this component of ice-surface slope is proportional to the absolute value of the slope of the linear displacement function in the gap. This ignores features such as the shape of the ice dam in Figure 8. In any case, the slope of the ice surface parallel to the lake increases in the gap as the flood grows and the gap width decreases.
As an example, assume a 60 m thick ice dam just west of Ro, corresponding to time t 2 in Figure 10. The average component of ice slope parallel to the lake boundary over the 85 km from Ro to Lo is then 7 × 10−4, or roughly the same order as a typical α value beneath grounded ice. Assuming the drumlins just west of Ro were formed at this time, drumlin orientations should be in the direction of the negative gradient of the displaced ice, i.e. shifted from normal to the lake boundary towards the west. This is in agreement with Figure 7. In addition, these gradient orientations should shift more towards lake parallel as g i moves towards Lo (Fig. 10). This is also in agreement with Figure 7, if the drumlins were created in a time-transgressive manner.
Phase II
Ice-dam build-up reduces the discharge over the Allegheny scarp; erosion beneath the sluice gate increases the discharge over the Niagara scarp. At some point the second process becomes dominant and the flow direction in the Lake Ontario basin shifts from east to west. Thereafter, the flood is termed phase II. (Sec the later discussion under Finger Lakes for another mechanism which can terminate phase I.)
The timing of the sluice-gate enlargement is very important. There are two limiting possibilities as well as intermediate states. First, the elapsed time for ice-dam build-up at the Allegheny scarp could be much shorter than the time for sluice-gate enlargement at the Niagara scarp. In this case, most or all exits from Lake Ontario are dammed during an interval between phases I and II. The water depth of the basin increases, perhaps by tens of meters. Subsequent opening of the sluice gate results in discharge of this stored water west into the Lake Erie basin, the phase II flood. This scenario is consistent with the previous explanation of drumlin orientations west of Rochester and is consistent with drumlin orientations at ?* west of Lake Ontario in Figure 7.
At the other extreme, the Niagara route opens up before significant ice-dam development takes place at the Allegheny scarp. The water level of the basin is probably not affected by dams. Phase I is short and discharge over the Allegheny scarp is much less than under the previous scenario. This does not fit the evidence of high-energy flow north of the Finger Lakes where large drumlins occur, and does not explain drumlin orientations at ?* in Figure 7.
There is some theoretical support for the first model. A water-sheet flood follows the hydrograph of a channelized flood because the flood issues from a subglacial lake in channelized form (Reference ShoemakerShoemaker, 1992a). The hydrograph of a channelized flood is determined by erosion of a channel in the ice as well as the substrate (Reference NyeNye, 1976). Similar erosional processes operate at the Niagara Escarpment to enlarge the sluice gate. The fact that erosion starts later at the sluice gate and is likely to lag behind erosion at the subglacial lake outlet suggests that the phase II flood could occur even after the peak of the water-sheet flood. In the following it is assumed that phase I is long, i.e. discharge over the Niagara scarp is restricted during the time of ice-dam build-up at the Allegheny scarp.
The bed-profile effect upon velocities
The largest drumlins near Lake Ontario are located east of Rochester, in a field up to 30 km deep down-glacier, but averaging about 20 km (Fig. 7). If a water sheet persisted during a displacement up to 30 km it is possible to show that water velocities much higher than normal existed over this field.
First, consider if a water sheet can be maintained during a 30 km displacement, or does ice-dam build-up terminate sheet flow? As an example refer to transect L2 in Figure 7, where ß 1 ≈ 10−2, ß 2 ≈ 0 and d ≈ 7.5 km in Figure 8 and the elevation of point B relative to A is 79 m. Thus the relief at summit a is 79 m relative to the surface of the ice lid. The maximum summit relief remains nearly constant for a displacement range of 7.5–28.5 km, or roughly the extent of the drumlin field. Down-glacier from 28.5 km the bed rises, so the ice-dam summit elevation grows for a displacement exceeding 28.5 km.
It would appear that for a water sheet to persist during a displacement up to 28.5 km, the water depth during flood maximum at point A in Figure 8 must be > 79 m. However, because ρ i/ρ w ≈ 0.9 this critical depth is decreased to about 71 m. As noted, the fictitious supraglacial flood is equivalent to the subglacial flood if ice thicknesses are reduced by 10%. Is a subglacial flood depth at A, or fictitious supraglacial flood depth at 0, of at least 71 m reasonable? There are two points to consider. First, if the subglacial lake lies outside the boundary of contemporary Lake Ontario by 3 km, for example, d is reduced by 3 km and the required minimum water depth at A (or O) is reduced to 42 m, which is well within calculated sheet thicknesses. Second, assuming the discharge out of the basin is restricted at the Niagara Escarpment and with a dam evolving at the Allegheny Escarpment basin, water-depth values increase, as previously noted. Only if this occurs can the discharge out of the basin increase to roughly balance the discharge into the basin. Rough equality must be maintained, recognizing that there is basin storage. An additional basin-head increase by 20 m when outflow is most impeded is not unreasonable. A 10 m increase brings the required minimum additional head at A due to water-sheet flow to 32 m in the example. A water sheet which reaches about 30 km down- glacier from Lake Ontario and which persists during an ice displacement of about 30 km cannot be ruled out.
Figure 8 illustrates how ice with a gradient of α when grounded becomes ice with a gradient of ß 1 – ß 2 + α when transported over a plateau with bed slope ß 2, connected to the basin by a steep ramp of bed slope ß 1 > ß 2. On transect L2 (Fig. 7) ß 1 – ß 2 ≈ 102. From Equations (2) and (3) the corresponding water-sheet velocity is doubled as compared to the velocity beneath ice with gradient α ≈ 10−3. Even if α ≈ 102 the velocity is increased by 20%. As noted earlier, drumlin formation is thought to be related to high-velocity flows, perhaps over a brief period. It is tempting to speculate that displacements by up to 30 km of steep ice were responsible for the large drumlins east of Rochester.
Finger Lakes
The Finger Lakes (and other similar lakes) are immediately down-glacier from the drumlin field just considered (Fig. 7). Reference Gilbert and Shaw.Gilbert and Reference ShawShaw (1994) reviewed evidence which points to either glacial scouring or subglacial fluvial erosion as the agent which created these basins, some of which extend below sea level. There are reasons to expect channelized fluvial erosion where the lakes are located.
It is known that the characteristic time for existence of a water sheet decreases rapidly with increasing α (Reference ShoemakerShoemaker, 1991). Consequently, the switch from unstable sheet flow to stable channel flow normally occurs first at the terminus and advances up-glacier. Channel flow is encouraged by the additional factor that the relief of bed hills exceeds 10 m in the Finger Lakes region and this relief increases down-glacier. Contours of bed relief are roughly parallel to the northern boundary of large hills (Fig. 7). Therefore, local grounding should occur in the zone extending from the Finger Lakes region to the terminus, particularly after ice displacement. Displacement brings the mechanism of Figure 9 into play, and grounding becomes more pervasive. Grounding produces preferred flood paths which develop into channels. Because large channels grow at the expense of small ones, channels tend to become widely spaced.
Channels can be incised either into the bed (Nyc (N) channels) or into the ice (Röthlisberger (R) channels). Because R channels move with the ice, they tend to become removed from the water source, namely, the water sheet. This factor is partially counteracted by R-channel extension up-glacier, but it takes time to enlarge an R channel. Because their location on the bed is fixed, N channels should be the preferred channel form when the bed is easily erodible and the ice rapidly moving.
Once a bed channel is created by one flood, it acts as a channel in a subsequent flood. This occurs to some extent even though the channel is initially infilled by ice, because once displacement occurs, thick ice is replaced by thinner ice at the up-glacier end of the channel and flow subsequently converges towards the channel. By this means, bed channels tend to propagate in the up-glacier direction over repeated floods.
During an outburst flood, subglacial channels operate at pressures lower than the overburden pressure until sudden channel closure occurs by ice infill (Reference NyeNye, 1976). This implies that the phase I flood over the Allegheny scarp could be terminated by channel closure down-glacier from the ice dam in Figure 8. The conjecture is that the Finger Lakes may be remnant bed channels or tunnel valleys, formed by fluvial erosion near the terminus of an ice sheet (or sheets).
Lake Erie
The megagrooves on Kelleys Island and neighboring islands in western Lake Erie can be connected to the phase II flood from Lake Ontario into Lake Erie. An outline is given here. First, consider restrictions on discharge from the Lake Erie basin. To the west, between Toledo and Sandusky, there are no constraints on either discharge or ice displacements (Fig. 7). To the east of Lorain the southern basin margin is high-banked with escarpments and hilly terrain (Fig. 7). Discharge should be restricted by the sluice-gate damming mechanism associated with a pinned state. Consequently, during both phases I and II there should be basin How from east to west. During phase II the westward component of basin flux should be large, at least as far west as Kelleys Island, because the discharge into the basin from the main southward water sheet plus the discharge from Lake Ontario have unimpeded outflow only to the west of Lorain (Fig. 7).
The Lake Erie basin is shallow. Taking an average depth of 20 m for the contemporary lake and performing the same calculation as done previously for Lake Ontario gives m ≈ 2.3 × 104, as compared to m ≈ 1.7 × 10−5 for Lake Ontario. Corresponding to this larger m value and q = 300 m2 s1, the head drop over the 320 km from the eastern end of the lake to Kelleys Island is about 73 m. During the phase II flood, if the westward component of basin flux is, on average, >300 m2 s1 the eastern lake level would be more than 73 m higher than the western lake level. The megagrooves are oriented between 240° and 260° (Reference GoldthwaitGoldthwait, 1979). This is consistent with a flow westward in the basin and discharging down-glacier between Toledo and Sandusky (Fig. 7).
Ice displacement accounts for locally high-velocity (debris-laden) flows over these islands. The situation of the bed humps in Figure 9b applies. After ice displacement the water-sheet thickness, y, narrows locally over an island by the value of the island relief, about 20 m. If flow divergence around an island does not markedly reduce q over the island, Equation (4) implies that V increases with 1/y so that high velocities can occur over the islands.
Ice displacements in other great lakes basins
Ice displacements were not included in the consideration of Lake Michigan. Nevertheless, displacement should accompany a water-sheet flood since the general broadening of the basin down-glacier (Fig. 5) limits side constraints. Ice displacement offers an alternative explanation of the lack of drumlins in the lee of Lake Michigan because an ice dam would severely restrict flow to the Ice of the basin.
The case of Lake Superior is the opposite. Here the basin narrows towards the lee end (Fig. 5) so that ice displacements would be minimal and no ice dam should develop. This observation is consistent with the presence of drumlins in the lee of Lake Superior.
Related Matters
Additional conclusions can be drawn. Those related to erosion and the situation at upflow-facing escarpments are addressed briefly. In addition, some explanation is given regarding drumlin presence in regions where subglacial lakes were unlikely and the ice topography was probably not unusual.
Green Bay and Grand Traverse Bay, Lake Superior
Figures 3 and 4 suggest that Green Bay and Grand Traverse Bay in Figure 5 are the products of fluvial scour from water-sheet floods interacting with an ice lid over the Lake Michigan basin. Major flood routes beneath supraglacial troughs coming off the upper Lake Michigan basin are predicted to exist in the approximate locations as Green Bay and Grand Traverse Bay (Figs 2b, 3 and 4). Because of the orientation and shape of Lake Michigan (Fig. 5), the western flood route is the preferred route. Green Bay to the west is larger than Grand Traverse Bay. Future floods should enlarge these bays, as suggested by Figure 4.
The convergent flow in the tapered western arm of Lake Superior (Fig. 5) has been noted. High flux and discharge at the lee end suggest past basin erosion and extension there from water-sheet floods. Future floods should continue this extension. On the other hand, ice displacement and flow divergence at the lee end of Lake Michigan, previously noted, should limit its enlargement in the southerly direction.
Upflow-facing escarpments
Rock flutings and drumlins are particularly well developed downflow from the crests of upflow-facing escarpments (Shaw and Gilbert, 1990; Reference Raukas and Tavast.Raukas and Tavast, 1994). Reference Pollard, Wakarani., Shaw., Ashworth, Bennet., Best. and McLelland.Pollard and others (1996) attribute this to vortex generation at escarpments. There is a related issue which has not been noted by others.
As mentioned previously, an ice sheet is pressed against an escarpment during a water-sheet flood. Water escaping over the escarpment does so by confined flow in narrow apertures. Because of the high local velocities the water pressure in these apertures is much less than the overburden pressure. Very intense localized turbulence as well as cavitation should be present. The localized nature of erosion, presumably by horseshoe vortices, is shown in Raukas and Tavast (1994, Fig. 2).
If an ice sheet is floated over the escarpment by deep water, the situation on the escarpment trends towards a conventional water sheet. However, the sheet thickness is narrow there so that velocities are still locally high, but not likely to be as high as when the sheet is pinned.
Drumlins where the ice profile is not unusual
Many drumlin fields occur outside regions of possible large subglacial lakes. Two examples are considered to illustrate that other mechanisms, besides unusual ice-sheet topography, may be present in drumlin formation.
(a) Drumlin fields nearly cover Finland and the Karelia and Kola peninsulas (Reference PunkariPunkari, 1982). These fields are generally fan-shaped and were evidently formed at different times because fans are truncated by overlying fans (Reference PunkariPunkari, 1982). If each fan field is the result of a flood, one must first explain why there were more than a dozen floods. Second, because most of the drumlin fields exceed 200 km in the direction of ice flow, ice displacement can be ruled out as the agent which produced high velocities. How can high velocities over such large distances be explained? A summary of results is given here. The complete development is lengthy.
The evidence is consistent with a number of supraglacial lakes discharging at different times to the bed by outburst floods through vertical channels, similar to conventional outburst floods (Reference NyeNye, 1976), except that the hydraulic gradient along the vertical channel is relatively large. The important results are: (1) The supraglacial lake discharges to the bed in less than 1 day, regardless of lake size. (2) To a first approximation, an instant subglacial lake is created which discharges down-glacier as a water-sheet flood. A channelized flood can be ruled out because it takes time to erode channels. In addition, the “instant” subglacial lake causes ice lift-off. (3) The flood is similar to the classic open-channel dam-break flood (Reference Henderson.Henderson, 1966). Velocities are very high over the entire flood distance. (4) A fan-shaped flood results from the fact that the flood is (instantly) deep and narrow at its origin and spreads out downstream. It is possible that the New England drumlin fields have a similar origin since interacting fans are present.
(b) The Livingstone Lake field of very large depositional drumlins is too wide, at least 150 km, to have its origin in a flood from a supraglacial lake and too long to be explained by ice displacement. At present, the best explanation is that the “surprisingly friable” (Reference ShawShaw, 1983) sandstone bed produced a sand-laden water sheet which was very abrasive and which eroded the drumlin cavity molds (Reference ShoemakerShoemaker, 1995). Note that bed erosion did not create bed forms but rather produced the erosion tools.
Conclusions
It is difficult to produce examples which establish the credibility of drumlinization by water-sheet action and which also rule out drumlinization by the conventional ice-contact model. For example, the present development explains the connection between subglacial lakes and drumlin orientations and, in some cases, field locations and drumlin size near these lakes. However, many of the results related to drumlin orientation can be transferred to the ice-contact model because the ice-surface gradient direction is the key variable in both models. There are, however, several examples developed here which do not fit the conventional model well.
(1) The megagrooves on the islands in western Lake Erie are explained by the present model but represent a major puzzle to anyone trying to explain their formation by ice contact (Reference GoldthwaitGoldthwait, 1979). For example, high-energy water discharge westward along the Lake Erie basin has no parallel in ice flow. (2) The abrupt change in drumlin orientations at moraines I and M (Fig. 5) does not require the assumption of independent lobes moving at right angles, as does the conventional model. (3) The orientation of drumlins west of Rochester and west of Lake Erie (Fig. 7) is, in my opinion, difficult to explain by the conventional model. (4) The locations of the Finger Lakes, Green Bay and Grand Traverse Bay are a natural outgrowth of the present model. It is difficult to explain these locations if the basins are the product of glacial scour. (5) I can find no explanation in the literature for the absence of drumlins in the lee of Lake Michigan. The water-sheet model predicts an absence of drumlins in this and other non-drumlinized regions. (6) The explanation given here for the genesis of the Finnish fan-shaped drumlin fields does not invoke the notion of numerous narrow ice lobes which were active during deglaciation (Reference PunkariPunkari, 1982).
Acknowledgements
This work was supported by a grant from the Canadian Natural Sciences and Engineering Research Council. I thank the reviewers for asking some difficult questions. The editor, M. Hambrey, was of great assistance in offering detailed comments.












