Thermal convection in ice sheets

In recent correspondence to the Journal, Hughes (2012) asked whether ice-stream tributaries are the surface expression of thermal convection rolls in the Antarctic ice sheet. The short answer to this is ‘no’. Ice sheets exhibit a slow viscous shallow flow which is driven by the shear stresses induced by the surface slope of the flow. Convection is a motion whose stresses are generated by horizontal thermal gradients through the action of buoyancy. On the face of it, they have nothing to do with each other.

This is the instinctive reaction of the dynamicist, and Hughes’s proposal, preceded by his earlier enquiries (Hughes, 1976, 2009), has not attracted much attention. The texts of Cuffey and Paterson (2010) and Hooke (2005) provide no index reference to convection. The web of science lists fourteen citations of the article by Hughes (1976), of which four are by Hughes himself, eight deal with ice on the satellite moons of the outer planets,* one by John Shaw concerns drumlins and megaflutes, and one is a review by Bob Thomas. It seems fair to say that Hughes’s hypothesis concerning the Antarctic ice sheet has not received much interest from theoreticians.

Hughes suggests two field experiments to test his hypothesis that thermal convection occurs in the Antarctic. The purpose of my correspondence is to propose a third test: nature can only do what the laws of physics allow it to do, and so Hughes’s hypothesis should first be judged on whether it is theoretically possible. I will provide a theoretical framework within which one may examine his proposal, though I stop short of providing a full numerical investigation of the resulting mathematical model.

The first port of call is an estimate of the Rayleigh number, ^† defined by

(1)

where α is the (volumetric) coefficient of thermal expansion, ΔT is the temperature difference between base and surface, ρ is the ice density reference value, g is the acceleration due to gravity, d is the ice depth, η is the ice viscosity, and κ. is the thermal diffusivity. If we suppose Glen’s law

(2)

with n = 3, A = 2.4 × 10⁻²⁴ Pa⁻³ s⁻¹ at 0°C (Cuffey and Paterson, 2010) and a typical basal shear stress of 0.5 × 10⁵ Pa for Antarctic inland ice, then η ∼ 0.83 × 10¹⁴ Pa s. We use values α ∼ 1.5 × 10⁻⁴ K⁻¹ (Butkovich, 1959, p.12; Cuffey and Paterson, 2010; note these authors quote the linear coefficient, which must be multiplied by 3 to obtain the usual volumetric coefficient), ρ ∼ 0.9 × 10³ kg m⁻³, g ∼ 9.8 m s⁻¹, K ∼ 10⁻⁶ m² s⁻¹, d = 3000 m and ΔT ∼ 50 K. Our first surprise is that the resultant estimate for the Rayleigh number is Ra ∼ 2.2 × 10⁴, which is enough to support convection (which typically sets in for Ra ≳10³). Conditions elsewhere are less favourable. In a Siple Coast (Antarctica) ice stream, if we take τ = 10⁴ Pa, d = 1000 m, ΔT ∼ 20 K, the resultant estimate is only Ra ∼ 13. We therefore focus on these ‘inland ice’ parameter values.

However, the situation in an ice sheet is a little different. The basic flow is a sloping flow (i.e. one whose basic motion is due to a downslope gravitational component), and, as Hughes points out, in this case convection sets in as rolls whose axes are aligned with the direction of the basic flow (Hart, 1971). However, Hart’s case is fundamentally different, since the sloping flow itself is driven by the temperature difference; in an ice sheet, this is not the case.

We can thus ask, is the buoyancy term large enough to cause convection in an ice sheet? We can initially frame this question within the context of a two-dimensional ice-sheet flow in the coordinates (x, z), in which the reduced pressure (i.e. with cryostatic component subtracted) is p, and the deviatoric components of the shear stress are τ ₁₁ and τ ₁₃. As normal in fluid mechanics, the pressure is minus one-third of the trace of the stress tensor. We assume the density is

(3)

and we write

(4)

where ΔT is the prescribed temperature difference. The momentum equations are scaled as in Fowler (2011, p. 631), and this leads to the dimensionless equations

(5)

in which the lettered subscripts denote partial derivatives (with respect to x or z), and where the ‘Rayleigh’ number is

Typical values of the aspect ratio are ε ∼ 1.9 × 10⁻³, if d = 3000 m, l = 1600 m, while the buoyancy number

(7)

so R ∼ 2100. The approximate solution of Eqn (5) is just

(8)

where z = s is the top surface, but although this is large, it has little effect because the corresponding approximate form of Eqn (5) ₁ is

(9)

and the buoyancy-induced stresses are small because B ≪ 1. So from a continental scale perspective, convection is absent.

Small-Scale Convection

To be fair, Hughes (2012) is not advocating convection on the continental scale indicated above, but rather is advocating small-scale convective rolls aligned with kilometres-wide fine-scale tributaries that are revealed in the astonishing figure 1 of his paper (but which, incidentally, are not visible in the presumably lower-resolution image at the web page he cites,* and which latter has also been published (Rignot and others, 2011)). This is analogous to the proposition by Parsons and McKenzie (1978) that small-scale convection in the form of rolls aligned with lithospheric plate motion might occur, and account for anomalous heat transport in tectonic plates.

In order to consider this possibility, we repeat our scaling argument. We are now in three dimensions, with the x axis pointing downstream, y across stream and z upwards. Corresponding deviatoric stresses are τ ₁₁, τ _12, etc., and the velocity components are u downstream and v = (v, w) transverse. With a constant viscosity η, we scale the equations, written in terms of the reduced pressure

(10)

by choosing

(11)

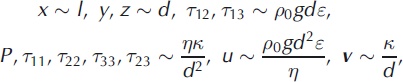
where d is the depth scale, l is the downstream length scale and

(12)

The choice of scale for the downstream stresses τ ₁₂, τ ₁₃ is motivated by the appropriate balance of the downstream shear stress gradient with the gravity-induced cryostatic pressure gradient; the scales for the transverse stresses are just the usual choice when studying thermal convection. The resulting equations take the form

(13)

where ∇ = (∂ _y , ∂ _z ), and the Peclet number is defined by

(14)

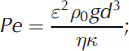
ε and Ra are as defined in Eqns (12) and (1). The equations are written out in full to highlight the role of the Peclet number, which is not usually present in studies of convection.

Using the values d = 3000 m, l = 1600 km (consistent with a choice τ ∼ ρ ₀ gdε = 5 × 10⁴ Pa), η = 0.83 × 10¹⁴ Pa s, we find

(15)

If we ignore the small ε ² terms, then the equations may be simplified to

(16)

and the free surface is given by the mass conservation law,

(17)

where we assume a flat base, z = 0. It is simplest to analyse Eqn (16) if we suppose Pe is small. This is apparently not the case, although we may note that, allowing for the dependence of η on τ ∝ d ² and ε ∝ d, we have Pe ∝ d ⁹, and even a change to d = 2000 m changes Pe to 0.25. We will discuss the model on the basis that Pe is small, and hope that the discussion can extend to the case Pe≳O(1). If Pe is small, the transverse flow problem reduces to a standard Rayleigh– Bénard convection problem, for which the onset of convection occurs at Ra≳1100. This suggests that, in fact, transverse convective rolls are quite possible, and that Hughes’s suggestion has merit. ^†

Reality Checks

However, the behaviour of ice is more complicated than this. Most importantly, the viscosity of ice depends on temperature, such that a 50° change in temperature causes a three order of magnitude change in viscosity. This has the effect of hindering convection. If we adopt as viscosity the value at the (warm) base (as we have already done), then we can assess the critical value of Ra from figure 4 of Solomatov (1995). That figure provides a regime diagram for temperature-dependent viscous convection, with axes being the Rayleigh number computed using the basal viscosity, Ra, and the multiplicative viscosity contrast Δη from the base to the top surface. The diagram is based on a series of numerical computations, and provides an approximate graph marking the onset of convection. It is this information that we use. For a viscosity contrast of Δη ∼ 10³, the critical (basal viscosity) Rayleigh number is ∼4 × 10⁴. This suggests that in fact convection is unlikely, as our estimate of Ra is about half this. (In fact, Solomatov’s result is for free-slip boundary conditions, but this may be roughly appropriate for wet-based ice. A no-slip condition would increase the critical value further.)

A further complication is that ice viscosity also depends on stress, with Glen’s law having exponent n = 3. The alert reader will observe that Solomatov also gives results for this case, and his figure 8 (whose comportment is similar to that of his figure 4) suggests that for n = 3, the critical Ra drops to 200! Is Hughes vindicated? No. In the stress-dependent viscosity case, there is no predefined stress, and thus no predefined basal viscosity. Examination of Solomatov’s definition of Ra in his eqn (51) shows that

(18)

where τ is the stress used in defining the stress-dependent basal viscosity. Thus we regain the previous definition if we choose the stress

(19)

Together with a basal viscosity given by Eqn (2), this allows us to find η, which turns out to be 2.6 × 10¹⁶ Pa s, whence in fact Ra ∼ 14, still well short of the onset of convection (at Ra = 200).

Actually, this stress-dependent calculation is inappropriate, because in our case there is a known background (downslope) stress, which indeed determines the viscosity. The transverse stress scale in Eqn (11), assuming η = 0.83 × 10¹⁴ Pa s, is ∼9 Pa, which is much less than the downslope stress. Consequently, the effect of this background stress, which varies linearly from the base to the surface, is to provide a further vertical variation of viscosity which enhances that due to temperature. The nonlinear calculation in Eqn (18), and the data in Solomatov’s figure 8, are only relevant where the stresses are those due entirely to convection, which is not the present situation. Therefore we revert to his figure 4, with the added variation that the stress variation from base to surface causes a further enhancement of the viscosity variation.

Halfway to the surface the shear stress is half its basal value, and the viscosity has increased by a factor of four due to this. With a similar change to the surface (an underestimate), the viscosity increase due to stress is a factor of 16, suggesting an effective value of Δη ∼ 1.6 × 10⁴. Consulting Solomatov’s figure 4 again, we find that this places the critical basal Rayleigh number at ∼10⁵. Even with a basal stress of 5 × 10⁴ Pa, Ra is still less than this value.

Hughes’s (2012) proposition of small-scale convection in ice sheets does not appear as unlikely as might at first be thought. However, my conclusion is that it is unlikely; at least, based on the simplest physical considerations. And if it does occur, the temperature and stress dependence of ice viscosity are likely to limit transverse circulation to the more fluid ice near the base, because, as realized by Hughes (1976) himself, the convection will be of the ‘stagnant lid’ type (Solomatov and Moresi, 1997), because the upper cold thermal boundary layer is very viscous and prone to stagnate.

But the real killer for this idea is that, if transverse convection does occur, it is at best marginal. That is to say, our estimates of Ra are such that, even if the critical value for convection is exceeded, the resulting dimensionless convective velocities (in Eqn (16)) will be of O(1), corresponding (see Eqn (11)) to dimensional transverse velocities of the order of . The corresponding transverse shear stresses will be of the order of . The elevation difference which such stresses support across a convective roll follows from a balance between the excess cryostatic pressure due to the uplift and the deviatoric transverse shear stresses generated, and is . Convection will have no significant effect on the ice motion or topography. The ice would follow a gentle corkscrew motion as it flows off the continent. At a speed of 100 m a⁻¹, it takes 10 000 years to travel 1000 km downslope. In that time, a transverse velocity of 10⁻² m a⁻¹ causes a transverse displacement of 100 m.

Hughes’s image of the convective tendrils of the Antarctic ice sheet is very persuasive of the phenomenon he hypothesizes. But I do not believe this image is an accurate representation of reality, at least as presently understood, nor am I adequately persuaded that the convective rolls which he hypothesizes, even if they occur, will have any significant imprint on the ice-sheet dynamics.