Using Linear Discriminant Analysis to Classify Snowfall Situations into Avalanching and Non-Avalanching Ones

Abstract

The existing methods of predicting avalanche danger often do not meet users’ demands because of the empiric character of the insufficient volume of information used. In such forecasts the contribution of each individual parameter into the prognostic information is unknown, and this is very important when studying such an event as avalanche formation, which is conditioned by a complex interaction of numerous factors, including snow accumulation, snow thickness, and the conditions of its development. It is obvious that such problems can be successfully solved by statistical methods, and that explains the growing interest in numerical methods of avalanche forecasting. Problems of multi-dimensional observations arises in many scientific fields. The method suited for this problem is discriminant analysis, the purpose of which is to divide a multi-dimensional observation vector into predetermined classes.

This study considers the prognostic (diagnostic) problems of fresh-snow avalanches released during snowfall or in the two days after it has ceased. The theoretical basis is a complex of statistical methods: correlation and dispersion analysis, “sifting” for the choice of predictors’ informative groups, construction of linear parametric discriminant functions, predictions based on training sample, and verification of discriminant functions based on independent material.

The archive used in the study consisted of 500 avalanching cases and 1 300 non-avalanching ones. All situations were grouped according to geomorphological characteristics. Each situation is described by eight meteorological characteristics. The results of classification of snowfall situations into avalanching and non-avalanching ones are as follows: reliability of p is from 75% to 91%, H from 0.15 to 0.51; based on independent material the reliability of p is from 63% to 85%, H from 0. 10 to 0.56.

Résumé

Les méthodes existantes pour la prévision du danger d’avalanche ne satisfont pas toujours à la demande des usagers en raison du caractère empirique du volume insuffisant d’informations utilisées. Dans les prévisions de l’espèce, la contribution de chaque paramètre particulier au pronostic est inconnue alors qu’elle est très importante dans l’étude d’évènements comme la formation d’avalanches régie par des interactions complexes entre de nombreux facteurs, chutes de neige, épaisseur du manteau, conditions de son développement. Il est clair que de tels problèmes peuvent être résolus avec succès par des méthodes statistiques, ce qui explique un intérêt croissant pour les méthodes numériques de prévision d’avalanches. Des problèmes d’observations multidimensionnelles se posent dans beaucoup de disciplines scientifiques. La méthode convenable pour de tels problèmes est l’analyse discriminante dont l’objectif est de diviser le vecteur observations multidimensionnelles en classes préétablies.

Cette étude considère les problèmes de pronostic (diagnostic) des avalanches de neige fraîche se produisant pendant une chute de neige ou dans les deux jours qui suivent. La base théorique est une réunion de méthodes statistiques: analyses de corrélation et de dispersion, “test” pour le choix des groupes d’informations prédicteurs, construction de fonctions discriminantes de paramètres linéaires, prévisions basées sur des essais sur échantillons, et vérification des fonctions discriminantes sur la base de matériels indépendants.

La population utilisée dans cette étude comprenait 500 cas d’avalanches et 1300 cas de non-avalanches. Toutes les situations ont été groupées selon leurs caractéristiques géomorphologiques. Chaque situation est décrite par huit caractéristiques météorologiques. Les résultats de la classification des situations de chute de neige en avalancheuses et non-avalancheuses sont les suivants: la fiabilité de p va de 75% à 91 %, celle de H de 0,15 à 0,51; à partir de données indépendantes, la fiabilité de p est de 63% à 85%, celle de H de 0,10 à 0,56.

Zusammenfassung

Infolge ihres empirischen Charakters oder wegen zu geringen Informationsvolumens werden die verfügbaren Methoden zur Vorhersage von Lawinengefahr oft den Anforderungen der Interessenten nicht gerecht. Bei Vorhersagen dieser Art ist der Anteil jedes einzelnen Parameters an der prognostischen Information unbekannt; dies ist von grosser Bedeutung für das Studium von Ereignissen wie der Lawinenbildung, die vom komplexen Zusammenwirken vieler Faktoren wie Akkumulation, Zusammensetzung und Metamorphose des Schnees abhängt. Offensichtlich können solche Probleme erfolgreich mit statistischen Methoden gelöst werden, woraus sich das wachsende Interesse der letzten Zeit an Rechenmethoden in der Lawinenvorhersage erklärt. Im vorliegenden Fall handelt es sich um die Unterscheidungsanalyse zur Aufspaltung eines vieldimensionalen Beobaehtungsvektors in vorbestimmte Klassen. Diese Untersuchung gilt dem Problem der Vorhersage von Neuschneelawinen, die während oder bis zu zwei Tagen nach Ende eines Schneefalles abgehen. Die theoretische Grundlage ist ein Komplex von statistischen Methoden: Korrelations- und Dispersionsanalyse; Filterung zur Auswahl der zur Vorhersage geeigneten Informationsgruppen; Aufbau linearer Parameter der Unterscheidungsfunktionen; Vorhersage auf der Basis von Lehrstichproben und Erprobung der Unterscheidungsfunktionen mit unabhängigem Material.

Das benutzte Archiv enthält 500 Fälle mit und 1 300 Fälle ohne Lawinen. Alle Hänge sind nach geomorphologischen Kennzeichen eingruppiert und nach 8 meteorologischen Verhältnissen beschrieben, Die Ergebnisse der Hangklassifizierung hinsichtlich ihrer Lawinengefahr sind die folgenden.

Die Zuverlässigkeit p liegt zwischen 75 und 91%; H ist 0,15-0,51; mit unabhängigem Material liegt p zwischen 63 und 85%; H ist 0,10–0,56.

The aim of discriminant analysis is to divide X vector-predictors into classes by an optimal method according to the prescribed predictant classes; the discriminant function makes it possible to determine the class of any X that is not included into the archive.

The simplest solution of the problem concerning the division of the object into classes is obtained with normally-distributed continuous predictors, identical covariant matrices within both classes of the object, and with inequality of mathematical expectations within the classes. In this ease the problem is solved by means of a linear parameter discriminant function U(X) that may be considered as some one-dimensional variable with normal distribution. The equality of the covariant matrices of different classes is a rather strong limitation, but it essentially simplifies the computational technique.

Non-significance of the differences between them is defined empirically, and then one matrix is constructed by averaging (taking the weights into consideration) the same elements. Another limitation is connected with the deviation from normal distribution that is conventional for some parameters.

Discriminant analysis methods are widely used in hydrometeorology (Gruza, 1967; Suzuki, 1969; Bois and Obled, 1973). Its application is simplest for forecasting of phenomena which assume alternative formulation. In this case the linear discriminant function at the limit of classes is:

where M ₁ and M ₂ are vectors of mathematical expectations within classes ϕ₁ and ϕ₂ respectively; II₁ and II₂ are a priori probabilities of classes ϕ₁, and ϕ₂; C ₁ and C ₂ are values of erroneous classification of the first and the second kind, their relation is assigned according to a priori probabilities of classes and valuability of correct prediction of each class; C ₁ is the value of the erroneous classification of the first kind which means that the X vector belonging to the first class is referred to the second one; C ₂ is the value of the erroneous classification of the second kind which means that the X vector belonging to the second class is referred to the first one. These errors arise due to the fact that the probability density of different classes is in some way recovered by each other. By means of the C ₂ /C ₁ correlation it is possible to improve results of correct identification of one class by deterioration of results of identification of the other class. The prime is the transposition sign and A is a vector of linear coefficients

where S denotes the mean covariant matrix.

Whether the concrete realization of the X vector belongs to classes ϕ₁, and ϕ₂ is determined by the following decisive rule: if U(X) ≥ R, then class ϕ₁ is forecast (i.e. avalanching is expected); if U(X) < R, then class ϕ₂ is forecast (i.e. avalanching is not expected).

R denotes the threshold value of the discriminant function

The purpose of the study was to classify the situations into avalanching and non-avalanching ones during snowfall (zero earliness forecast or diagnosis of the fresh-snow avalanches which slipped during snowfall or within the next two days when there was no rise in temperature). The concept “zero earliness forecast” can be explained as follows. Let us analyse the object which is described by observing parameters y = (y1, y2, …,ym); these observations can be referred to the different moments of time t_yi, j = 1, …, m. Suppose that we have clarified the physical nature of this object and can describe it by another one X = (x₁, x₂, …, x_n ), i.e. the characteristics of the X objects are also referred to different moments of time t_xi, i = 1, …, n If

then the analysis can be regarded by its character as prognostic.

Otherwise extrapolation in time and, consequently, the prediction is not possible. Let us assume that when

the time interval

indicates the forecast earliness, the moment of time

represents the moment of forecasting and the time interval

indicates the forecasting period or period of forecasting efficiency.

The case when the requirement

is not realized, i.e. τ < 0, is also interesting, and generally it is in accordance with the problem of statistical analysis or diagnosis. Sometimes it is called “zero earliness forecast”.

Investigations were carried out on the basis of observed data obtained from snow-avalanche stations in Central Asia. For the analysis samples consisting of 500 cases of avalanching (class ϕ₁) and 1 300 cases of non-avalanching (class ϕ₂) were used. All data were differentiated into two altitude zones (higher and lower than 3 000 m) and into three sectors in each altitude zone. The first sector united cases of situations observed on slopes of southern aspect (S., S.E., and S.W. expositions), the second one covered cases with western and eastern aspects, and the third sector united cases observed with northern aspects (N., N.E., and N.W. expositions). The values of the vector-predictor in each zone differs in the variable quantity X ₈ (the sum of the total daily radiation during the period of snowfall, which depends on the slope aspect). The whole totality of avalanches was considered as one case, if some avalanches were observed in similar height conditions and orographic aspect.

A vector whose components are analogue data on meteorological conditions in which the formation of a fresh snow layer occurs and which have decisive influence on avalanche formation in fresh snow, is taken as a predicting vector (predictor) X = (x₁, x₂, …, x_k ), k = 1,…,8. The variables x₁, x₂, x₃ are introduced into the prediction scheme to characterize indirectly the state of the old-snow surface at the beginning of snowfall. Table I gives the content of the predictor.

Table I. The meaning of the predictors used

Discriminant analysis provides for two stages according to the scheme used: training and control testing. Training implies the first stage of the experiment when the training is carried out on the basis of predictor sampling with a known division into classes, i.e. the correlational analysis is realized, the covariance matrix is constructed, the predictors are sifting, the coefficient of the discriminant function and the indicator of divisibility (NR) are assessed. The stage of control testing includes the assessment of the reliability sample forecasts on dependent and independent material. The material is referred to as “dependent” if the training is carried out including it; “independent” material is material not included in the training stage, but used for testing of the discriminant functions constructed on the basis of dependent material.

Different statistical characteristics are considered within each stage. “Double ‘Student’s’ t-criterion” determines divergence variability of

the arithmetic mean values of samples obtained from the results of independent measurements. This is one means of predictor informativity and serves as an assessment of the possibility of their application for classification of situations into classes ϕ₁ and ϕ₂ classes during snowfalls.

The calculations showed that considering error probability from 0. 10 to 0.05 for predictors x₄–x₈, the difference in ihe means of samples of classes ϕ₁ and ϕ₂ is mainly significant; insignificant differences prevail for predictors x ₁–x ₃, this indicates their low informativity according to this criterion.

Informativity of different prcdictor groups was defined by a “sifting method” that includes the definition of a division index (NR):

where

are mean values of discriminant function within classes ϕ₁ and ϕ₂;

(Mahalanobis distance), and D is the dispersion of the linear discriminant function within both classes. The “sifting” method consists of the following procedures. First all the components of the X vector are inspected and a component is chosen that provides the best classification into classesϕ₁ and ϕ₂((NR) value being taken as a criterion). Then U(X) is calculated for the chosen component together with each other one. The pair which gives maximum (NR) value is taken as the optimal one. The optimal pair is used to choose an optimal triple, etc.

In Table II the results of “sifting” arc presented for six samples, where the predictors are set in the order of their choice at “sifting”, P _T in this table denotes the theoretical probability of correct classification (Gnedenko, 1965).

Table II. Comparative informativity of different- predictors

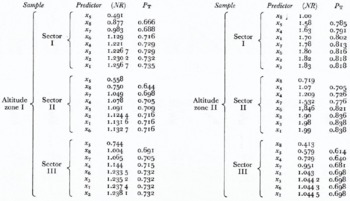
The data presented in Table II which show the degree of informativity increasing (through (NR)) as each predictor is added, allow us to conclude that the optimal informativity group (in the given complex) is obtained by means of variables characterizing the total value of precipitation, solar radiation, absolute air humidity, precipitation duration, and, in three of the six cases chosen, the sum of daily mean air temperatures. The order of these variables determined by their informativity rank was different in the two altitudinal zones.

In the altitude zone higher than 3000 m, the classification of snowfall situations depends greatly upon precipitation value, while in the zone lower than 3000 m it depends upon solar radiation. In the first zone during the third step of “sifting” the x₇ variable, the sum of daily mean absolute air humidity, was chosen; in the second zone this variable entered the optimal complex only in the fourth step.

At the boundary of this group the growth of theoretical forecast reliability essentially stops. This is rather important when defining the optimal group of predictors which is included into forecast, because introduction into the prediction scheme of features insignificantly affecting the classification quality, leads to the deterioration of the reliability of the forecast on independent material, although the forecast based on dependent material can be improved to some extent.

The predictors which were not included into the optimal complex include the variables x₁, x₂ and x₃ indirectly characterizing the state of the old-snow surface before the snowfall began.

The next stage of the experiment consisted of making a forecast on the basis of the training sample, and for this purpose the discriminant function value was found, and the classification of situations into avalanching and non-avalanching ones with different values of C ₁, and C ₂ was made using the rule mentioned above. The best results for satisfactory classification of situations into the two classes were obtained with the values of the erroneous classification inversely proportional to the class of the appearance probability (except sector II in the altitude zone II, where the best result was obtained with a lower ratio C ₁/C ₂).

Table III shows the forecast estimation based on the training sample at various C ₁/C ₂ ratios and with either eight- and five-dimensional vector predictors for the sectors of the first altitude zone in order to estimate the effect of the dimension N_x of the vector-predictor on the forecast result (when N_x = 5, the predictors which were not introduced in Table II, were excluded).

Table III. Estimation of success of classification of situations during snowfalls into avalanching and non-avalanching ones

The following symbols are used in Table III:

Table IV. Estimation of success of classification of situations during snowfalls into avalanching and non-avalanching ones based on independent material

This last criterion is more effective for assessing avalanche prediction, as is obvious, for instance, from the forecast result for sector II of altitude zone II, where at p = 90.9%, H equals only 0.15%. The high percentage of forecast reliability with a low value of the H criterion in this case was due to successful prediction of class ϕ₂ with a comparatively small number of cases in class ϕ₁.

As a rule forecasts made by discriminant functions constructed on independent material proved to have less reliability, but quite comparable with the reliability of an avalanche forecast by any other empirical method, and testifies to the usefulness of the proposed method. The forecast results on independent samples are given in Table IV.