Introduction
Glacial lakes are indicators of climate change because their expansion or contraction reflects variations of water balance and heat condition in mountains (Reference Shi and RenShi and Ren, 1990). In the Himalaya, a number of glacial lakes, of which moraine- dammed lakes are the most common type, have recently appeared and expanded in and around alpine glaciers (Reference Che, Jin, Li and WuChe and others, 2004;Reference Chen, Cui, Yang and QiChen and others, 2005;Reference Lu, Yao, Wang, Liu and GuoLu and others, 2005;Reference KomoriKomori, 2008;Reference Sharma, Sakai, Nuimura, Yamaguchi and SharmaSharma and others, 2009;Reference Gardelle and Arnaud Yand BerthierGardelle and others, 2011). These expanding glacial lakes are often surrounded by steep slopes and contained by fragile moraines that are prone to failure. Devastating events (e.g. rockfalls, glacier calving and avalanches into the lake area) can create large waves and trigger flooding due to washout (Reference Awal, Nakagawa, Fujita, Kaiwake, Baba and ZhangAwal and others, 2010). In the past 50 years, >35 large glacial lake outburst floods (GLOFs) have taken place in the Himalayan region, many of which caused great damage not only to the local catchment but also to the surrounding lowlands far beyond the limits of the lake area (Reference Xu and FengXu and Feng, 1989;Reference Clague and EvansClague and Evans, 2000;Reference CarrivickCarrivick, 2010;Reference Shrestha, Eriksson, Mool, Ghimire, Mishra and KhanalShrestha and others, 2010). Meanwhile, small-scale GLOFs occur almost every year, usually going unnoticed because of the limited damage caused or because of their remote location (ICIMOD, 2007). GLOFs and related debris flows play a dominant role in mountain disasters in the Himalaya (e.g. Reference Xu and FengXu and Feng, 1989; Reference Ding and LiuDing and Liu, 1992; Reference Fujita, Suzuki, Nuimura and SakaiFujita and others, 2008;Reference Bajracharya and MoolBajracharya and Mool, 2009). Numerous studies have confirmed that temperature increase in the Himalayan region has been greater than in other areas at the same latitude (Reference Zheng, Lin and ZhangZheng and others, 2002;Reference Singh and BengtssonSingh and Bengtsson, 2005; Reference LiLi and others, 2011), and the rate of warming has been almost twice the rate of global warming since the 1950s (0.23 vs 0.13°C per decade) (Reference YangYang and others, 2006). During recent decades, glaciers in this region, as in many other regions worldwide, have experienced accelerated recession (Reference Pu, Yao, Wang, Su and SengPu and others, 2004;Reference Zhang, Fang, Zhao and ZengZhang and others, 2010). Given rapid warming and glacier retreat, it is anticipated that glacial lakes will continue to expand into the areas between receding glacier fronts and terminal moraines, and that GLOFs will become more frequent (Reference Richardson and ReynoldsRichardson and Reynolds, 2000;Reference HaeberliHaeberli and others, 2004;Reference YaoYao and others, 2010). We therefore need improved monitoring of moraine- dammed lakes and a better understanding of GLOF mechanisms (Reference ReynoldsReynolds, 1998;Reference He, Ma, Cui and ChenHe and others, 2002;Reference Chen, Cui, Yang and QiChen and others, 2007; Reference Wang and LiuWang and Liu, 2007).
Accurate estimation of the storage capacity of moraine- dammed lakes is essential for predicting flood peak discharge, simulating flood evolution and establishing early warning systems (Reference Bajracharya, Mool and ShresthaBajracharya and others, 2007;Reference Ng, Liu, Mavlyudov and WangNg and others, 2007). As suggested by previous studies (Reference Chen, Lu, Cai, Li and YinChen and others, 2008; Reference Fujita, Suzuki, Nuimura and SakaiFujita and others, 2008), the volume of moraine-dammed lakes can be estimated from digital elevation models (DEMs) using reservoir capacity methods based on a grid, cross sections or contours. The volume of Telamukanli lake in the upper stream of Yarkant river, for example, was calculated using a cross-section method in a field study in 1987 (Reference Shi, Yang, You and JinShi and others, 1991). In addition, Reference EvansEvans (1986) and Reference Huggel, Kaab, Haeberli and Teysseire Pand PaulHuggel and others (2002) proposed an empirical relationship between glacial lake volume and area. For the moraine-dammed lakes in the Himalayan region, due to their harsh climate and remoteness, there is often a shortage of ground-based monitoring data, especially lake water depth (Reference Wang, Liu, Yao, Guo, Yu and XuWang and others, 2010). So far, in situ measurements of lake water depth have only been conducted at a few glacial lakes on the south side of the Himalaya (Reference BhargavaBhargava, 1995;Reference YamadaYamada, 1998;Reference Mool, Bajracharya and JoshiMool and others, 2001;Reference Sakai, Fujita, Yamada and MavlyudovSakai and others, 2005). They have not yet been carried out on the north side, so there is little knowledge of the morphology and storage capacity of moraine-dammed lakes in this region.
In this study, we first report the results of in situ surveys conducted in September 2009 on Longbasaba lake in Dinggyê Country, Tibet. Based on the water depth data collected by the SyQwest HydroboxTM portable high-resolution shallow-water echo sounder, we model the morphology of the lake basin by constructing a triangulated irregular network (TN), and calculating its volume. By inter-preting multi-source remote-sensing images, we also analyze the history of Longbasaba lake. Finally, we propose an empirical formula for the volume-area relationship of Longbasaba lake by assuming that the lake basin is in steady state.
Study Area
Longbasaba lake (27°57'17" N, 88°04'55" E) is located at the headwaters of the Geiqu river, a tributary of the Yeruzangbu river in the Pumqu river watershed. Its altitude was 5499 m a.s.l. in 2009, with a length of 2210 m from north to south and a width of 685 m from east to west. The lake is dammed by an end moraine formed by modern glaciation (Fig. 1). On the southwest side of Longbasaba lake, there is another moraine-dammed lake, Pida lake, at 5564 m a.s.l. The distance between the two lakes is ~335 m. The recharge of Longbasaba lake has two main sources: glacier meltwater and precipitation. The terminus of Longbasaba glacier, with abundant crevasses, stretches into the lake in the southeastern corner. Many serac clusters and small supraglacial lakes develop on the glacier. Ice floes of various sizes from glacier disintegration float on the lake.

Fig. 1. Location of Longbasaba lake, the potentially GLOF-affected region and its status. (Photo taken from dam by Yao)
According to observations by the local water conservation office, Longbasaba lake grew rapidly in 2004, putting its dam at risk of failure (Reference Li and ZhangLi and Zhang, 2008;Reference Wang, Liu, Guo and XuWang and others, 2008). A hazard investigation report on the lake issued by the Hydrological Department of the Tibet Autonomous Region in 2006 pointed out that a flood would threaten the towns of Saer and Jiangga, where Dinggyê County center was located, along with 23 other downstream villages, and would destroy roads, bridges and communication facilities between the city of Shigatse and Dinggyê County and the Rongkong hydropower station. Hence, there is an urgent need to monitor the variations in Longbasaba lake.
Data and Methods
In situ survey data
In September 2009, extensive in situ surveys of the water depth of Longbasaba lake were conducted using the SyQwest Hydrobox™ portable high-resolution shallow- water echo sounder. This instrument is designed exclusively for inshore and coastal hydrographic marine surveys in water depths of 800 m. The measuring system consists of a laptop computer, an echo sounder, an eTrex VistaTM GPS receiver and a powered rubber dinghy. As shown in Figure 2, the echo sounder was installed on the right side of the head of the rubber dinghy, to reduce as far as possible disturbance to the transducer from bubbles produced by the propeller. As the rubber dinghy moved, we continually examined water depth values displayed on the laptop screen to ensure that the transducer was completely submerged and its radiant surface was parallel to the water surface. The sonar system's position was acquired with the eTrex Vista GPS receiver, with a horizontal precision of about 3-6 m. The GPS receiver was installed on top of the transducer support to ensure that its location was consistent with the measuring point. The course of the rubber dinghy was set to give a uniform distribution of measuring points, with first measurements along the lake boundary. To ensure the transducer was always submerged in water and to prevent the transducer and propeller from hitting rocks under the surface, a distance of at least 2-5 m was always maintained between the rubber dinghy and the lake bank. The rubber dinghy moved in a zigzag pattern along the minor axis of the lake and a U-shape course along the major axis, with a total of 35 558 measurement points collected (Fig. 3). Due to frequent collapses of ice bodies and the resulting huge waves, we did not measure the inaccessible parts near the glacier terminus. Furthermore, to verify the accuracy of the sonar depth data, 33 random points were measured using a measuring rope. The estimated mean error was 1-2 m, so the sonar data were considered to be highly accurate.

Fig. 2. The rubber dinghy used in the field investigation, and schematic of measuring system.
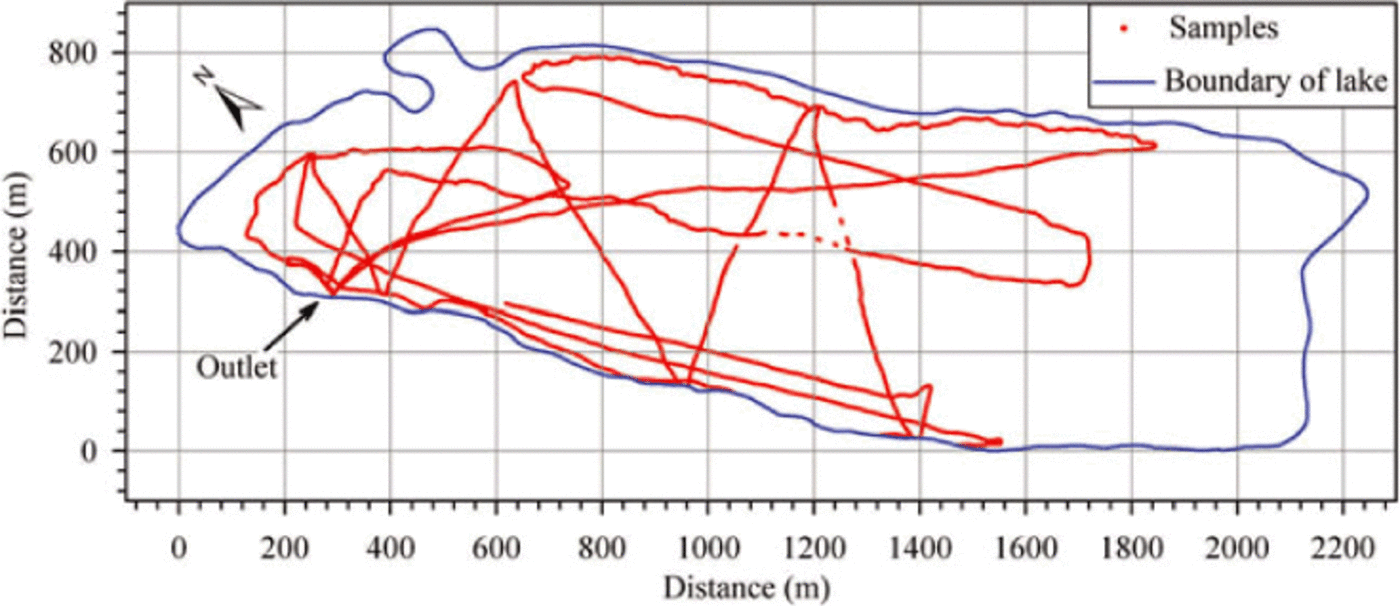
Fig. 3. The distribution of sampling points (red circles) of the sonar system. The blue line is the lake boundary derived from Landsat TM in November 2009.
Remote-sensing image and topographic map
During the fieldwork, large amounts of gravel and rocks fell into the lake from the steep flanks, which hindered spatial data collection along the lake boundary. In fact, our rubber dinghy was once damaged by falling rocks. As an alternative data collection method, we downloaded a Landsat Thematic Mapper (TM) image (path 139, row 41) acquired on 9 November 2009 from the United States Geological Survey (USGS) website (http://glovis.usgs.gov) as a reference. From the same website we also downloaded other remote-sensing images of Longbasaba lake: one Landsat Multispectral Scanner (MSS) image, three Landsat TM images and five Landsat Enhanced TM Plus (ETM+) images. Four Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images were bought from USGS. We also used a topographic map, dated 1980, at a scale of 1 : 50 000. Details of these images are shown in Table 1. Remote-sensing images concentrated mainly on November and December, as well as May and January when the lake was frozen.
Table 1. Topographic map and satellite remote-sensing data.

All Landsat images listed in Table 1 were registered digitally to the 2009 Landsat TM scene (which is used as the 'base') using a cubic polynomial model in ENVI software, by selecting 10-15 ground-control points that were clearly identifiable in both images, with most of the points chosen on stable terrain adjacent to Longbasaba lake. The registration error was 0.8 pixel (23 m) when registering the MSS image to the TM image, and 0.5 pixel (14 m) when registering the TM/ETM+ image to the TM image. The topographic map was scanned at 300dpi and spatially referenced to the TM image using the thin-plate spline model. Contours on the topographic map were then delineated to interpolate the DEM, which was used in the process of Terra ASTER image orthorectification. Similarly, Terra ASTER images were referenced to the 2009 TM base image, with a registration accuracy of 0.5 pixel, or 14 m. After this pre-processing, the Longbasaba lake boundary in different years was digitized and geometric parameters such as area and length were calculated in ArcGIS software.
Error in the lake extent from remote-sensing image interpretation was controlled by the image resolution and co-registration error (Reference Hall, Bayr, Schoner, Bindschadler and ChienHall and others, 2003). From Reference Williams, Hall and ChienWilliams and others (1997):

where d is the linear dimension error, λ is the original pixel resolution of each image (28.5 m for TM or ETM+ data, 15 m for ASTER data and 57 m for MSS data) and e is the registration error. Thus the accuracy is actually ±54m for Landsat TM and Landsat ETM+ data, ±35 m for Terra ASTER data and ±103 m for Landsat MSS data.
Changes in the areal extent of Longbasaba lake were measured with an accuracy of ±0.0023 km2 for Landsat TM and ETM+ images, ±0.0092 km2 for the Landsat MSS image and ±0.0006 km2 for the Terra ASTER images, with error, a, in the area given by (Reference Hall, Bayr, Schoner, Bindschadler and ChienHall and others, 2003)
where A = λ2 and d is the error in the linear dimension from Eqn (1).
Data processing
In total, 6916 discrete measurement points were obtained. The maximum depth measured was 102 ± 2 m, and the average depth was 48 ± 2 m. This is 18 ± 2 m deeper than measured by Reference Liu and SharmaLiu and Sharmal (1988), who found an average depth of 30m during their expedition to the glacier lakes in the Pumqu (Arun) and Poiqu (Bhote-Sun Kosi) river basins.
Three-dimensional coordinate data (x, y, depth) of the 6916 discrete points and vector data of the lake boundary were processed using ArcGIS software. The elevation of each point in the lake basin was calculated from the difference between the altitude of the water surface, obtained by GPS, and the depth value obtained by the sonar system. ATIN was built using the ArcGIS 3-D Analyst Module. The digitized boundary of Longbasaba lake derived from the Landsat TM image of 2009 was a constraint on the TIN boundary, with the depth assumed to be zero. Based on the assumptions that (1) the lake basin is in steady state, (2) the part of the lake basin outside the vectorized boundary line for a given year is filled by the glacier, and (3) the water level does not change, the volumes of Longbasaba lake in different years were then calculated using a GIS overlay analysis.
Results and Discussion
Morphology modeling of Longbasaba lake
Based on the TIN data, the basin morphology of Longbasaba lake was modeled as indicated in Figure 4. It is apparent that the basin bottom of the lake is relatively flat and its flanks are steep, with slopes ranging from 28° to 30°. The southeastern side is steeper than the northwestern side. From the water depth profile it is seen that the depth slowly increases from moraine dam to glacier terminus in the frontal 550 m, then suddenly drops to reach the bottom of the lake. The depth varied from 86 to 101 m at a distance of 1000-1850 m from the moraine dam (Fig. 5). As there are no measurements at the junction of the lake and the glacier terminus, changes in depth were represented as a linear decrease in this area, due to the assumption of zero water depth at the lake boundary.
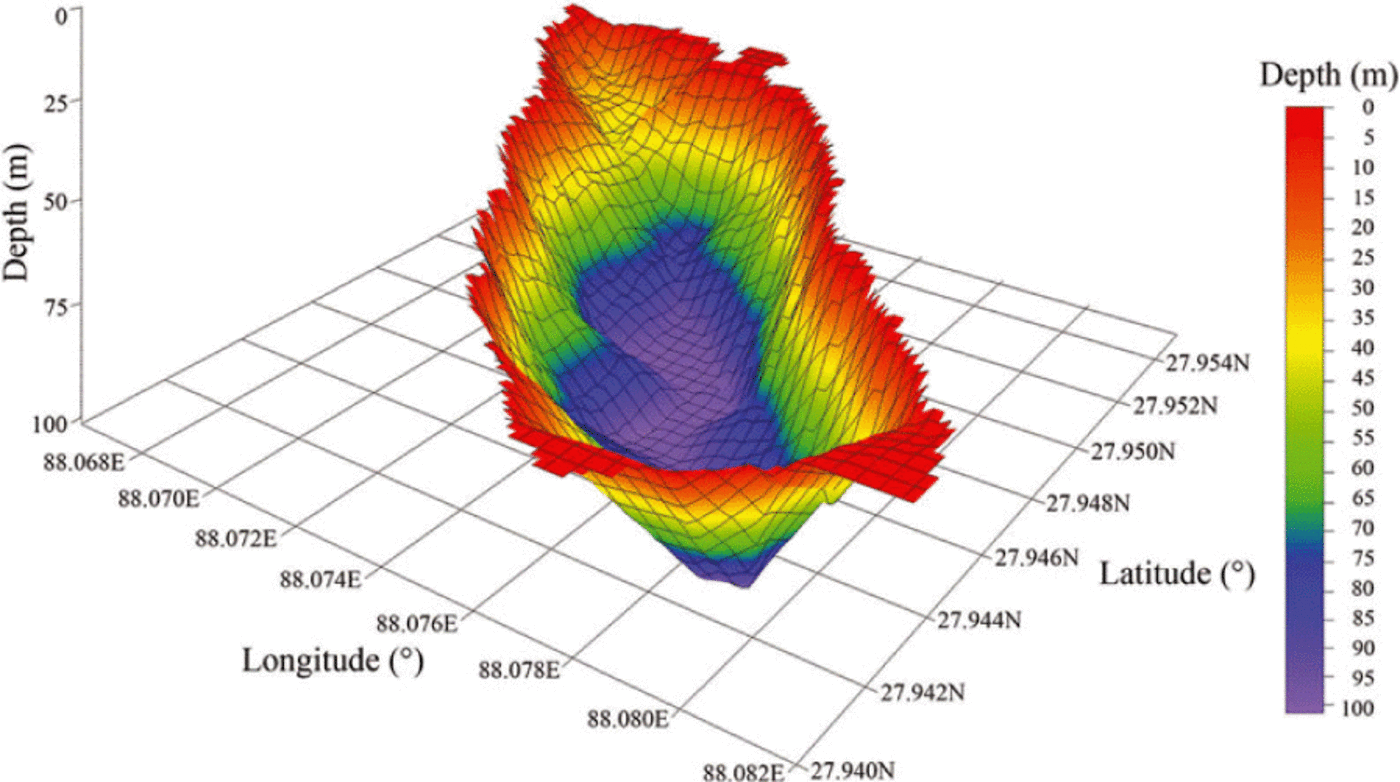
Fig. 4. Morphology modeling of Longbasaba lake in 2009 (viewing angle is from south to north).

Fig. 5. Profile map of Longbasaba lake water depth from the moraine dam to the glacier terminus in 2009.
Spatio-temporal changes of Longbasaba lake
Results of the remote-sensing investigation suggest that the length and area of Longbasaba lake have increased over the past 32 years. In 1977, the length and area were 946 ± 103 m and 0.3320 ± 0.0092 km2, respectively. By 2009 these values had increased to 2210 ± 54 m and 1.2187 ± 0.0023 km2. This represents proportional changes in length and area of 137±32% and 267± 11%. During the study period, the average annual changes were 39.50 ± 5ma-1 and 0281 ± 0.0004 km2 a-1. Over the period 2000-09, these changes reached 58 ± 6 m a-1 and 0.0355 ± 0.0003 km2 a-1, about three times and twice as high, respectively, as the values over the period 1977-80. As can be seen from Figure 6, the variations in length and area during 2000-09 can be divided into three phases:
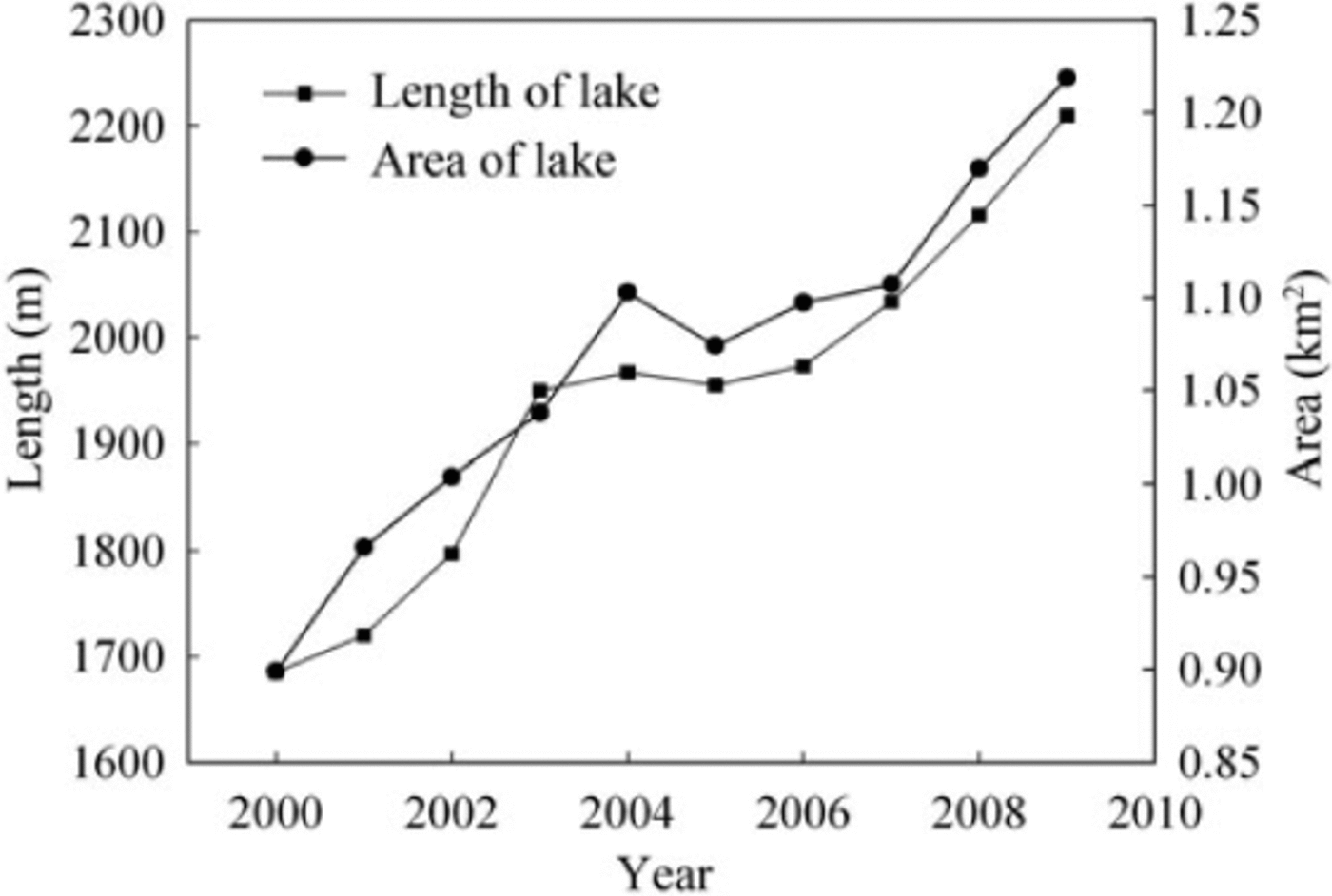
Fig. 6. Changes in the length and area of Longbasaba lake from 2000 to 2009
-
1. 2000-04: the lake was in a state of rapid expansion. Its length and area increased by 282 ±45 m and 0.2041 ± 0.0003 km2, at rates of 71 ± 22 m a-1 and 0.0510 ± 0.0001 km2 a-1, respectively. The total proportional changes were 16.74± 3% and 22.71 ± 0.68%. This finding corresponds well with the result reported by the local water resource department (Reference Li and ZhangLi and Zhang, 2008; Reference Wang, Liu, Guo and XuWang and others, 2008).
-
2. 2005-07: the lake was in relatively steady state. In 2005, its length was 1955 ± 35 m, slightly less than in 2004. Its area decreased accordingly, from 1.1029 ± 0.0006 km2 to 1.0739 ± 0.0006 km2. This change was probably the result of the drainage measures conducted by the Department of Water Resources of Tibet Autonomous Region in 2005 (Reference Li and ZhangLi and Zhang, 2008). In the following years, the lake expanded again, but at a slower rate than during the first phase. Until 2007, its area was about the same as in 2004.
-
3. 2008-09: the lake was again in a state of a rapid growth. The length and area rapidly increased, and the average annual changes amounted to 94 ±54ma-1 and 0.0488 ± 0.0023 km2 a-1, respectively, almost equivalent to those observed during the first period.
Figure 7 presents the spatial changes of the lake boundary. There is a clear trend that the lake grew as the glacier retreated. Many other Himalayan moraine-dammed lakes have been expanding as their associated glacier retreats (e.g. Tsho Rolpa, Imja and Luggye Tsho) (Reference Richardson and ReynoldsRichardson and Reynolds, 2000). It should be noted that the underside of the glacial cliff at the terminus of Longbasaba glacier has a concave shape, easily resulting in frequent collapses of ice bodies due to the calving process (Reference Benn, Warren and MottramBenn and others, 2007; Reference Sakai, Nishimura, Kadota and TakeuchiSakai and others, 2009;Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others, 2010). Once a huge amount of ice avalanches into the lake, it will cause a rapid rise in water level. However, there is to date no detailed information at the glacier/lake interface.
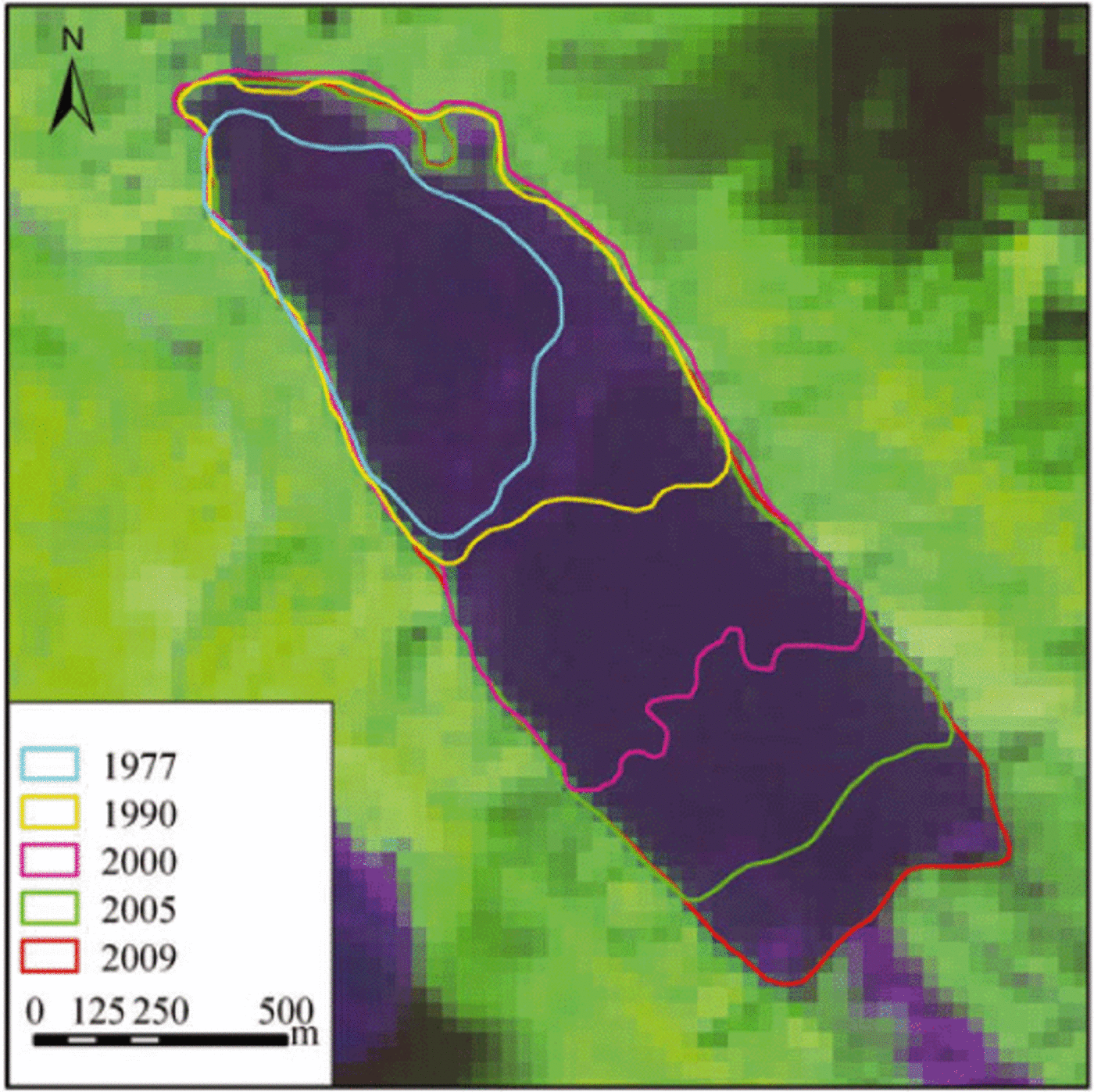
Fig. 7. Spatial variation of Longbasaba lake from 1977 to 2009 (composition of spectral bands of Landsat TMis 4,5,3).
Volume estimation of Longbasaba lake
The volume of a lake can be interpreted as the water volume between the surface and a datum surface of the lake basin (Reference Shi, Yang, You and JinShi and others, 1991). The volume of Longbasaba lake, 0.064 ± 0.002 km3 in 2009, was calculated using the surface elevation and the lake bed derived from the TIN. Note that the water depth near the glacier terminus was assumed to be zero in the morphology modeling, which probably leads to the actual volume of Longbasaba lake being underestimated. However, our calculation provides an approximate estimate of the magnitude of this moraine-dammed lake.
For the relationship between the lake volume and area, Reference Huggel, Haeberli, Kaab, Bieri and RichardsonHuggel and others (2004) have proposed an empirical formula based on a study of glacial lakes in North America, South America, Iceland and the Alps. When using this formula to estimate the volume of larger moraine-dammed lakes in the Himalayan region, there are obvious inconsistencies with the measured values. We therefore attempt to build an empirical formula of volume and area suitable for the investigated region. By comparing water depths at Imja lake on the south slope of the Himalaya obtained in 1992 and 2002 (Reference YamadaYamada, 1998;Reference Sakai, Fujita, Yamada and MavlyudovSakai and others, 2005), it was found that the morphology of the lake basin showed little change while the area changed substantially. We assume that the water level remains constant and calculate the storage capacity of Longbasaba lake in different years from vector data of the lake boundary. As shown in Figure 8, the regression between the volume and area of Longbasaba lake is

Fig. 8. Relationship between volume and area of Longbasaba lake for the period 1977-2009.
where V is the volume (km3), A is the area (km2), n is the number of samples and R2 is the coefficient of determination.
By using Eqn (3) and the formula suggested by Reference Huggel, Kaab, Haeberli and Teysseire Pand PaulHuggel and others (2002), we calculated the volumes of the moraine-dammed lakes in the Himalaya, for which we know storage capacities. The results indicate that the estimates using Eqn (3) are in good agreement with the observations, with the exception of lower Barun lake (Table 2). For lower Barun lake, the error ((calculated value- measured value)/measured value) was almost 40%. A likely explanation for this is that lower Barun lake is a supraglacial lake, not a moraine-dammed lake (Reference Mool, Bajracharya and JoshiMool and others, 2001). This, to some extent, also indicates that the storage capacity of moraine-dammed lakes is greater than that of supraglacial lakes. In addition, compared to the estimates using the formula suggested by Reference Huggel, Haeberli, Kaab, Bieri and RichardsonHuggel and others (2004), the error using Eqn (3) was smaller. This suggests that the relation shown in Eqn (3) can produce more reliable estimates of the volume of moraine-dammed lakes in the Himalaya than the relation of Reference Huggel, Haeberli, Kaab, Bieri and RichardsonHuggel and others (2004).
Table 2. Comparison of measured and calculated lake volumes for Himalayan morine-dammed glacial lakes

Conclusion
In this study, we have modeled the basin morphology of Longbasaba lake and analyzed changes, mainly variations in length and area during 1977-2009. The basin bottom of the lake is relatively flat and its flanks are steep. In 2009, the average depth of the lake was 48±2 m, with a maximum value of 102 ± 2 m. During recent decades, the lake has shown a considerable increase in length and area, and especially since 2000 it has exhibited a drastic expansion. We estimated the storage capacity of the lake using the water depth together with geographical information techniques including GPS, remote sensing and GIS. The lake volume was 0.064 ± 0.002 km3 in 2009. Using the estimates of area and storage capacity in different periods, we established a regression equation relating lake volume and area. Analysis of the volumes of measured moraine-dammed lakes in the Himalayan region shows that our formula performs better than that proposed by Reference Huggel, Kaab, Haeberli and Teysseire Pand PaulHuggel and others (2002). That is, our equation provides a relatively accurate method for calculating volumes of unmeasured moraine- dammed lakes in the Himalayan region.
Acknowledgements
This work was funded by the National Natural Science Foundation of China (No. 41071044), the Knowledge Innovation Project of the Chinese Academy of Sciences (CAS;No. KZCX2-YW-Q03-04), the National Basic Work Program of Chinese MST (No. 2006FY110200), the Program of Enhancing Young Teachers' Scientific Research Ability of Northwest Normal University (NWNU-LKQN-10- 35), the Natural Science Foundation for Post-doctoral Scientists of China (20100480731) and the Fund of the State Key Laboratory of Cryosphere Science (2010-05). We gratefully acknowledge Xiaofeng Deng, Haidong Han, Zhen Wu and Yinsong Zhang, from the Cold and Arid Regions Environmental and Engineering Research Institute of CAS, who gave us great help in the water depth measurement of Longbasaba lake. We thank two anonymous reviewers and the scientific editor, B. Kulessa, for helpful comments and suggestions. We also thank Roger J. Braithwaite, Qiao Liu and Yong Zhang for helping to polish the English












