Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Harju, Antti J.
2015.
Analysis of twisted supercharge families on product manifolds.
Journal of Mathematical Physics,
Vol. 56,
Issue. 4,
Mickelsson, Jouko
2017.
Extensions of lattice groups, gerbes and chiral fermions on a torus.
Journal of Geometry and Physics,
Vol. 121,
Issue. ,
p.
378.
Bunke, Ulrich
and
Nikolaus, Thomas
2019.
Twisted differential cohomology.
Algebraic & Geometric Topology,
Vol. 19,
Issue. 4,
p.
1631.
Becker, Kimberly E.
Murray, Michael K.
and
Stevenson, Daniel
2020.
The Weyl map and bundle gerbes.
Journal of Geometry and Physics,
Vol. 149,
Issue. ,
p.
103572.
Mickelsson, Jouko
and
Murray, Michael
2021.
Non-associative magnetic translations from parallel transport in projective Hilbert bundles.
Journal of Geometry and Physics,
Vol. 163,
Issue. ,
p.
104152.

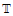 and a manifold
and a manifold 