Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T10:06:31.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic cycles satisfying the Maurer-Cartan equation and the unipotent fundamental group of curves

Published online by Cambridge University Press:  04 April 2013

Majid Hadian
Majid Hadian*
Affiliation:
University of Illinois at Chicago, Chicago, 60607 IL, USAhadian@math.uic.edu
Get access

Abstract

We address the question of lifting the étale unipotent fundamental group of curves to the level of algebraic cycles and show that a sequence of algebraic cycles whose sum satisfies the Maurer-Cartan equation would do the job. For any elliptic curve with the origin removed and the curve 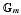, we construct such a sequence of algebraic cycles whose image under the cycle map gives rise to the étale unipotent fundamental group of the curve.

Keywords

Unipotent Fundamental GroupsAlgebraic CyclesMaurer-Cartan Equation and Massey Products14C25-14F42
Type
Research Article
Information
Journal of K-Theory , Volume 11 , Issue 2 , April 2013 , pp. 351 - 392
Copyright
Copyright © ISOPP 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Beilinson, A.; Vologodsky, V.: A DG guide to Voevodsky's motives. Geom. Func. Anal. 17 (6) (2008), 1709–1787.Google Scholar
2.Bloch, S.: Some elementary theorems about algebraic cycles on abelian varieties. Inventiones Mathematicae 37 (3) (1976), 215–228.Google Scholar
3.Bloch, S.: Algebraic cycles and the Lie algebra of mixed Tate motives. J. Amer. Math. Soc. 4(4) (1991), 771–791.CrossRefGoogle Scholar
4.Bloch, S.; Kriz, I.: Mixed Tate motives. Ann. of Math. (2) 140 (3) (1994), 557–605.CrossRefGoogle Scholar
5.Deligne, P.: Cohomologie étale, Séminaire de Géométrie Algébrique du Bois-Marie, SGA 4½, avec la collaboration de J. F. Boutot, A. Grothendieck, L. Illusie et J. L. Verdier, Springer Lecture Notes in Mathematics 569, Berlin-New York 1977.Google Scholar
6.Deligne, P.: Le groupe fondamental de la droite projective moins trois points. Galois groups over ℚ. (Berkeley, CA, 1987), Math. Sci. Res. I nst. Publ. 16, Springer, New York (1989), 79–297.Google Scholar
7.Deligne, P.; Goncharov, A.: Groupes fondamentaux motiviques de Tate mixte. Ann. Sci. École Norm. Sup. (4) 38 (1) (2005), 1–56.CrossRefGoogle Scholar
8.Faltings, G.: Mathematics around Kim's new proof of Siegel's theorem. Diophantine geometry, CRM Series 4, Ed. Norm., Pisa (2007), 173–188.Google Scholar
9.Geisser, T.; Levine, M.: The Bloch-Kato conjecture and a theorem of Suslin-Voevodsky. J. Reine Angew. Math. 530 (2001), 55–103.Google Scholar
10.Hadian, M.: Motivic Fundamental Groups and Integral Points. Duke Mathematical Journal 160(3) (2011), 503–565.Google Scholar
11.Kimura, K.; Terasoma, T.: Relative DGA and mixed elliptic motives. Preprint. Available at arXiv: 1010.3791v3Google Scholar
12.Levine, M.: Tate motives and the fundamental group. Cycles, motives and Shimura varieties, Tata Inst. Fund. Res. Stud. Math. Tata Inst. Fund. Res., Mumbai (2010), 265–392.Google Scholar
13.Suslin, A., Voevodsky, V.: Relative Cycles and Chow Sheaves. Cycles, transfers, and motivic homology theories, Ann. of Math. Stud. 143, Princeton Univ. Press, Princeton, NJ, (2000), 10–86.Google Scholar
14.Voevodsky, V.: Triangulated categories of motives over a field. Cycles, transfers, and motivic homology theories, Ann. of Math. Stud. 143, Princeton Univ. Press, Princeton, NJ (2000), 188–238.Google Scholar