Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T13:01:41.814Z Has data issue: false hasContentIssue false
  • English
  • Français

The equivariant index theorem in entire cyclic cohomology

Published online by Cambridge University Press:  28 May 2008

Denis Perrot
Denis Perrot
Affiliation:
Université de Lyon, Université Lyon 1, CNRS, UMR 5208 Institut Camille Jordan, 43, bd du 11 novembre 1918, 69622 Villeurbanne cedex, France, perrot@math.univ-lyon1.fr.
Get access

Abstract

Let G be a locally compact group acting smoothly and properly by isometries on a complete Riemannian manifold M, with compact quotient G\M. There is an assembly map 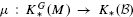which associates to any G-equivariant K-homology class on M, an element of the topological K-theory of a suitable Banach completion 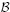of the convolution algebra of continuous compactly supported functions on G. The aim of this paper is to calculate the composition of the assembly map with the Chern character in entire cyclic homology 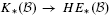. We prove an index theorem reducing this computation to a cup-product in bivariant entire cyclic cohomology. As a consequence we obtain an explicit localization formula which includes, as particular cases, the equivariant Atiyah-Segal-Singer index theorem when G is compact, and the Connes-Moscovici index theorem for G-coverings when G is discrete. The proof is based on the bivariant Chern character introduced in previous papers.

Keywords

K-theoryassembly mapentire cyclic cohomologyindex theory
Type
Research Article
Information
Journal of K-Theory , Volume 3 , Issue 2 , April 2009 , pp. 261 - 307
Copyright
Copyright © ISOPP 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Atiyah, M. F., Singer, I. M.: The index of elliptic operators. III, Ann. Math. 87 (1968) 546–609CrossRefGoogle Scholar
2.Baum, P., Connes, A.: Geometric K-theory for Lie groups and foliations, Brown University/IHES preprint (1982)Google Scholar
3.Baum, P., Connes, A., Higson, N.: Classifying space for proper actions and K-theory of group C*-algebras, Contemp. Math. 167 (1994) 241–291Google Scholar
4.Berline, N., Getzler, E., Vergne, M., Heat kernels and Dirac operators, Grundlehren des Mathematischen Wissenschaft 298, Springer-Verlag (1992)Google Scholar
5.Blackadar, B.: K-theory for operator algebras, Springer-Verlag, New-York (1986)CrossRefGoogle Scholar
6.Connes, A.: Non-commutative geometry, Academic Press, New-York (1994)Google Scholar
7.Connes, A.: Entire cyclic cohomology of Banach algebras and characters of θ-summable Fredholm modules, K-Theory 1 (1988) 519–548CrossRefGoogle Scholar
8.Connes, A., Moscovici, H.: Cyclic cohomology, the Novikov conjecture and hyperbolic groups, Topology 29 (1990) 345–388CrossRefGoogle Scholar
9.Connes, A., Moscovici, H.: Transgression and the Chern character of finite-dimensional K-cycles, Comm. Math. Phys. 155 (1993) 103–122CrossRefGoogle Scholar
10.Cuntz, J.: Bivariant K-theory for locally convex algebras and the Weyl algebra, preprintGoogle Scholar
11.Cuntz, J., Quillen, D.: Cyclic homology and nonsingularity, JAMS 8 (1995) 373–442Google Scholar
12.Fack, T., Kosaki, H.: Generalized s-numbers of τ-measurable operators, Pacific J. Math. 123 (1986) 269–300CrossRefGoogle Scholar
13.Gilkey, P.: Invariance theory, the heat equation, and the Atiyah-Singer index theorem, 2nd ed., Studies in Advanced Mathematics, CRC Press (1995)Google Scholar
14.Hörmander, L.: Fourier integral operators. I, Acta Math. 127 (1971) 79–183CrossRefGoogle Scholar
15.Jaffe, A., Lesniewski, A., Osterwalder, K.: Quantum K-theory, I. The Chern character, Comm. Math. Phys. 118 (1988) 1–14CrossRefGoogle Scholar
16.Kasparov, G. G.: An index for invariant elliptic operators, K-theory, and representations of Lie groups, Soviet Math. Dokl. 27 1 (1983) 105–109Google Scholar
17.Klimek, S., Kondracki, W., Lesniewski, A.: Equivariant entire cyclic cohomology: I. Finite groups, K-Theory 4 (1991) 201–218CrossRefGoogle Scholar
18.Klimek, S., Lesniewski, A.: Chern character in equivariant entire cyclic cohomology, K-Theory 4 (1991) 219–226CrossRefGoogle Scholar
19.Meyer, R.: Local and Analytic Cyclic Homology, EMS Tracts in Math. vol. 3, EMS Publishing House (2007)Google Scholar
20.Mishchenko, A., Fomenko, A.: The index of elliptic operators over C*-algebras, Izv. Akad. Nauk. SSSR, Ser. Mat. 43 (1979) 831–859Google Scholar
21.Perrot, D.: A bivariant Chern character for families of spectral triples, Comm. Math. Phys. 231 (2002) 45–95CrossRefGoogle Scholar
22.Perrot, D.: Retraction of the bivariant Chern character, K-Theory 31 (2004) 233–287CrossRefGoogle Scholar