Article contents
Equivariant Intersection Theory and Surgery Theory for Manifolds with Middle Dimensional Singular Sets
Published online by Cambridge University Press: 07 March 2008
Abstract
Let G denote a finite group and n = 2k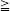 6 an even integer. Let X denote a simply connected, compact, oriented, smooth G-manifold of dimension n. Let L denote a union of connected, compact, neat submanifolds in X of dimension
6 an even integer. Let X denote a simply connected, compact, oriented, smooth G-manifold of dimension n. Let L denote a union of connected, compact, neat submanifolds in X of dimension 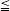 k. We invoke the hypothesis that L is a G-subcomplex of a G-equivariant smooth triangulation of X and contains the singular set of the action of G on X. If the dimension of the G-singular set is also k then the ordinary equivariant self-intersection form is not well defined, although the equivariant intersection form is well defined. The first goal of the paper is to eliminate the deficiency above by constructing a new, well defined, equivariant, self-intersection form, called the generalized (or doubly parametrized) equivariant self-intersection form. Its value at a given element agrees with that of the ordinary equivariant self-intersection form when the latter value is well defined. Let
k. We invoke the hypothesis that L is a G-subcomplex of a G-equivariant smooth triangulation of X and contains the singular set of the action of G on X. If the dimension of the G-singular set is also k then the ordinary equivariant self-intersection form is not well defined, although the equivariant intersection form is well defined. The first goal of the paper is to eliminate the deficiency above by constructing a new, well defined, equivariant, self-intersection form, called the generalized (or doubly parametrized) equivariant self-intersection form. Its value at a given element agrees with that of the ordinary equivariant self-intersection form when the latter value is well defined. Let 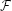 denote a finite family of immersions withtrivial normal bundle of k-dimensional, connected, closed, orientable, smooth manifolds into X. Assume that the integral (and mod 2) intersection forms applied to members of
denote a finite family of immersions withtrivial normal bundle of k-dimensional, connected, closed, orientable, smooth manifolds into X. Assume that the integral (and mod 2) intersection forms applied to members of 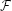 and to orientable (and nonorientable) k-dimensional members of L are trivial. Then the vanishing of the equivariant intersection form on
and to orientable (and nonorientable) k-dimensional members of L are trivial. Then the vanishing of the equivariant intersection form on 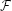 ×
×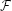 and the generalized equivariant self-intersection form on
and the generalized equivariant self-intersection form on 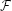 is a necessary and sufficient condition that
is a necessary and sufficient condition that 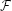 is regularly homotopic to a family of disjoint embeddings, each of which is disjoint from L. This property, when
is regularly homotopic to a family of disjoint embeddings, each of which is disjoint from L. This property, when 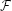 is a finite family of immersions of the k-dimensional sphere Sk into X, is just what is needed for constructing an equivariant surgery theory for G-manifolds X as above whose G-singular set has dimension less than or equal to k. What is new for surgery theory is that the equivariant surgery obstruction is defined for an almost arbitrary singular set of dimension
is a finite family of immersions of the k-dimensional sphere Sk into X, is just what is needed for constructing an equivariant surgery theory for G-manifolds X as above whose G-singular set has dimension less than or equal to k. What is new for surgery theory is that the equivariant surgery obstruction is defined for an almost arbitrary singular set of dimension 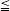 k and in particular, the k-dimensional components of the singular set can be nonorientable.
k and in particular, the k-dimensional components of the singular set can be nonorientable.
Keywords
Information
- Type
- Research Article
- Information
- Journal of K-Theory , Volume 2 , Special Issue 3: In Memory of Yurii Petrovich Solovyev October 8, 1944–September 11, 2003 , December 2008 , pp. 507 - 600
- Copyright
- Copyright © ISOPP 2008
References
- 2
- Cited by

