Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Farley, Daniel Scott
and
Ortiz, Ivonne Johanna
2014.
Algebraic K-theory of Crystallographic Groups.
Vol. 2113,
Issue. ,
p.
99.
Farley, Daniel Scott
and
Ortiz, Ivonne Johanna
2014.
Algebraic K-theory of Crystallographic Groups.
Vol. 2113,
Issue. ,
p.
45.

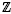 [
[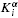 (
(