Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T16:37:01.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative Zariski Open Objects

Published online by Cambridge University Press:  31 January 2012

Florian Marty
Florian Marty*
Affiliation:
Laboratoire Émile Picard, Université Paul Sabatier, 118 route de Narbonne, 31062 Toulouse Cedex 04, Francefmarty9@ac-toulouse.fr
Get access

Abstract

In [TV], Bertrand Toën and Michel Vaquié define a scheme theory for a closed monoidal category (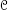,⊗, 1) One of the key ingredients of this theory is the definition of a Zariski topology on the category of commutative monoidal objects in 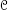. The purpose of this article is to prove that under some hypotheses, Zariski open subobjects of affine schemes can be classified almost as in the usual case of rings (ℤ-mod,⊗,ℤ). The main result states that for any commutative monoidal object A in 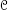, the locale of Zariski open subobjects of the affine scheme Spec(A) is associated to a topological space whose points are prime ideals of A and whose open subsets are defined by the same formula as in rings. As a consequence, we can compare the notions of scheme over 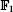in [D] and in [TV].

Keywords

Categoryenriched categorysievesrelative geometry
Type
Research Article
Information
Journal of K-Theory , Volume 10 , Issue 1 , August 2012 , pp. 9 - 39
Copyright
Copyright © ISOPP 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

B.Barr, M. - Exact categories - Springer, Lecture notes in mathematics 236, pp1–120, 1971.Google Scholar
BQ.Borceux, F., Quinteiro, C. - A theory of enriched sheaves - Cahiers de topologie et géométrie différentielle catégorique volume XXXVII-2, 1996, pages 145–162.Google Scholar
D.Deitmar, A. - Schemes over F 1 in: Number Fields and Function - Progress in Mathematics 239 Geer, Gerard van der; Moonen, Ben J.J.; Schoof, Ren (Eds.) 2005. Fields - Two Parallel Worlds.Google Scholar
G.Gabriel, P. - Des Catégories abéliennes - Bulletin de la société mathématique de France 90 (1962) pp 323–448.Google Scholar
SGA4.Artin, M., Grothendieck, A. et Verdier, J.L. - Théorie des topos et cohomologie étale des schémas. Tome 1: Théorie des topos - Séminaire de Géométrie Algébrique du Bois-Marie 1963-1964 (SGA4) - Lecture notes in mathematics 269 - Springer-Verlag, Berlin-New York, 1972. xix+525pp.Google Scholar
H.Hovey, M. - Model Categories - Mathematical Surveys and Monographs 63 - American Mathematical Society, Providence, RI, 1999. xii+209pp.Google Scholar
Kap.Kaplansky, I. - An introduction to differential algebra - Hermann, Paris, 1957.Google Scholar
K.Kelly, G.M. - Basic concepts of enriched category theory - London Mathematical Society Lecture Note Series 64 - Cambridge University Press, Cambridge-New York, 1982. 285pp. Also available in Reprints in theory and applications of categories 10(2005).Google Scholar
DK.Day, B.J., Kelly, G.M. - Enriched functor categories - Springer Lecture Notes in Mathematics 106 - Springer-Verlag, Berlin and New York, 1969. pp179–191.Google Scholar
McL.Mac Lane, S. - Categories for the working mathematician - Graduate text in mathematics 5 - Springer-Verlag, New York-Berlin, 1971. ix+262pp.Google Scholar
TV.Toën, B., Vaquie, M. - Au dessous de Spec(ℤ) - J. K-Theory 3 (2009), 437–500.Google Scholar