Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schochet, Claude L.
2014.
Banach algebras, Samelson products, and the Wang differential.
Journal of Topology and Analysis,
Vol. 06,
Issue. 02,
p.
281.
SETH, APURVA
and
VAIDYANATHAN, PRAHLAD
2023.
RATIONAL -STABILITY OF CONTINUOUS -ALGEBRAS.
Journal of the Australian Mathematical Society,
Vol. 115,
Issue. 1,
p.
119.
Seth, Apurva
and
Vaidyanathan, Prahlad
2023.
K-stability of AT-algebras.
Journal of Mathematical Analysis and Applications,
Vol. 522,
Issue. 2,
p.
126957.
Kawamura, Kazuhiro
2024.
HIGHER CONNECTED STABLE RANKS AND THEIR RATIONAL VARIANTS OF AF ALGEBRAS.
Rocky Mountain Journal of Mathematics,
Vol. 54,
Issue. 5,
Smrekar, Jaka
2025.
Spaces of functions and sections with paracompact domain.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 155,
Issue. 3,
p.
893.

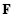 = ℝ or ℂ
= ℝ or ℂ