No CrossRef data available.
Published online by Cambridge University Press: 09 March 2023
Numerals and ordinals occupy a special place in the typology of suppletion. In generative work, one basic cross-linguistic parameter is whether ordinal allomorphy displays internal vs. external marking. Internal marking is when irregular forms propagate from lower ordinals to higher ones (English ‘first’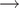 $ \to $‘twenty-first’), whereas external marking is the lack of propagation. We catalog ordinal formation in Armenian dialects through both formal-generative and functional-typological perspectives. We find that Eastern Armenian and Early Western Armenian are uniformly external-marking systems for the ordinals of ‘1–4’. However, Modern Western Armenian is a mixed system: ‘1’ displays external-marking while ‘2–4’ display internal-marking. Simultaneously, the ordinal of ‘1’ uses a suppletive portmanteau, while the ordinals of ‘2–4’ use agglutinative allomorphs. We formalize these differences in a derivational approach to morphology (Distributed Morphology). We argue that mixed systems arise from allomorphy rules that are sensitive to either constituency or linearity. The Western mixed system seems typologically rare and novel. Given our formal analysis, we then uncover other asymmetries in the propagation of irregular ordinals and the retention of portmanteau morphology across 35 Armenian varieties. The end result is a strong functional correlation between suppletion, external marking, and lower numerals.
$ \to $‘twenty-first’), whereas external marking is the lack of propagation. We catalog ordinal formation in Armenian dialects through both formal-generative and functional-typological perspectives. We find that Eastern Armenian and Early Western Armenian are uniformly external-marking systems for the ordinals of ‘1–4’. However, Modern Western Armenian is a mixed system: ‘1’ displays external-marking while ‘2–4’ display internal-marking. Simultaneously, the ordinal of ‘1’ uses a suppletive portmanteau, while the ordinals of ‘2–4’ use agglutinative allomorphs. We formalize these differences in a derivational approach to morphology (Distributed Morphology). We argue that mixed systems arise from allomorphy rules that are sensitive to either constituency or linearity. The Western mixed system seems typologically rare and novel. Given our formal analysis, we then uncover other asymmetries in the propagation of irregular ordinals and the retention of portmanteau morphology across 35 Armenian varieties. The end result is a strong functional correlation between suppletion, external marking, and lower numerals.