Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2025-01-02T21:30:36.807Z Has data issue: false hasContentIssue false
  • English
  • Français

An atomic model of crack tip deformation in aluminum using an embedded atom potential

Published online by Cambridge University Press:  31 January 2011

R. G. Hoagland ,
M. S. Daw ,
S. M. Foiles  and
M. I. Baskes
R. G. Hoagland
Affiliation:
Washington State University, Pullman, Washington 99164-2920
M. S. Daw
Affiliation:
Sandia National Laboratory, Livermore, California 94551-0969
S. M. Foiles
Affiliation:
Sandia National Laboratory, Livermore, California 94551-0969
M. I. Baskes
Affiliation:
Sandia National Laboratory, Livermore, California 94551-0969
Get access

Abstract

The atomic configuration at the tip of a mode 1 crack in aluminum is modeled by means of molecular dynamics calculations using an embedded atom potential. This potential intrinsically incorporates many-body contributions. This paper is concerned with the characteristics of the atomic displacement fields in comparison to the linear elastic predictions and dislocation emission phenomena. 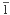Three crack/crystal orientations are examined in which the crack plane–crack propagation directions are (010)-[100], (10)-[110], and (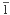10)-[111]. The first two models behaved in a brittle fashion as dislocation emission did not occur for reasons associated with the use of periodic boundary conditions parallel to the crack front. For the models which remained atomically sharp, the positions of the atoms near the crack tip in equilibrium configurations are different from the linear elastic predictions but, to first order, retain an r1/2 dependence, with smaller K, and with the origin displaced behind the physical crack tip. This near tip region is also observed to be elastically softer than in the far field. Dislocation emission readily proceeds in the (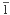10)-[111] model by the sequential emission of partials with attendant nonzero uz displacements. The blunting is characterized by the creation of two corner defects that separate as emission occurs and relaxation of the strains in the region initially confronted by the crack tip. Additional features of the results are discussed.

Type
Articles
Information
Journal of Materials Research , Volume 5 , Issue 2 , February 1990 , pp. 313 - 324
Copyright
Copyright © Materials Research Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1Thompson, R., J. Phys. Chem. Solids 48, 965 (1987).CrossRefGoogle Scholar
2Hirth, J.P., Hoagland, R.G., and Popelar, C.H., Acta Metall. 32, 371 (1984).CrossRefGoogle Scholar
3Thompson, R. and Sinclair, J. E., Acta Metall. 30, 1325 (1982).CrossRefGoogle Scholar
4Kelly, A., Tyson, W. R., and Cottrell, A. H., Phil. Mag. 15, 567 (1967).CrossRefGoogle Scholar
5Rice, J. and Thompson, R., Phil. Mag. 29, 73 (1974).CrossRefGoogle Scholar
6Lin, I-H., Mater, J.. Sci. Lett. 2, 295 (1983).CrossRefGoogle Scholar
7Dienes, G. J. and Paskin, A., J. Phys. Chem. Solids 48, 1015 (1987).CrossRefGoogle Scholar
8Sieradzki, K., Dienes, G.J., Paskin, A., and Massoumzadeh, B., Acta Metall. 36, 651 (1988).CrossRefGoogle Scholar
9Sinclair, J.E., Phil. Mag. 31, 647 (1975).CrossRefGoogle Scholar
10Kanninen, M. F. and Gehlen, P. C., in Interatomic Potentials and Simulation of Lattice Defects, edited by Gehlen, P. C., Beeler, J. R., and Jaffee, R.I. (Plenum Press, New York, 1971), p. 713.Google Scholar
11Gehlen, P. C., Hahn, G.T., and Kanninen, M. F., Scripta Metall. 6, 1087 (1972).CrossRefGoogle Scholar
12Mullins, M., Acta Metall. 32, 381 (1984).CrossRefGoogle Scholar
13deCelis, B., Argon, A. S., and Yip, S., J. Appl. Phys. 54, 4864 (1983).CrossRefGoogle Scholar
14Johnson, R. A., Phys. Rev. 6, 2094 (1972).CrossRefGoogle Scholar
15Harrison, W. A., Pseudopotentials in the Theory of Metals (Benjamin, New York, 1966).Google Scholar
16Messmer, R.P., Salahub, D.R., Johnson, K.H., and Yang, C.Y., Chem. Phys. Lett. 51, 84 (1977).CrossRefGoogle Scholar
I7Daw, M. S. and Baskes, M. I., Phys. Rev. 29, 6443 (1984).CrossRefGoogle Scholar
18Clementi, E. and Roetti, C., Atomic Data and Nuclear Data Tables 14, 177 (1974).CrossRefGoogle Scholar
19Rose, J. H., Smith, J. R., Guinea, F., and Ferrante, J., Phys. Rev. B 29, 2963 (1984).CrossRefGoogle Scholar
20Sih, G.C. and Liebowitz, H., in Fracture—An Advanced Treatise, edited by Liebowitz, H. (Academic Press, New York, 1968), Vol. II, p. 67.Google Scholar
21Sinclair, J.E. and Fletcher, R., J. Phys. C 7, 864 (1972).CrossRefGoogle Scholar
22Hoagland, R. G., Gehlen, P. C., and Hirth, J. P., Phil. Mag. 34, 413 (1976).CrossRefGoogle Scholar
23McCoy, J. K. and Markworth, A. J., Scripta Metall. 20, 905 (1986).CrossRefGoogle Scholar
24Irwin, G. R., Handbuch der Physik VI, Flugge ed. (Springer, 1958), p. 551.CrossRefGoogle Scholar
25Rice, J. R., J. Appl. Mech. 35, 379 (1968).CrossRefGoogle Scholar