Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T04:31:12.721Z Has data issue: false hasContentIssue false
  • English
  • Français

DFT based study on structural stability and transport properties of Sr3AsN: A potential thermoelectric material

Published online by Cambridge University Press:  29 April 2019

Enamul Haque Open the ORCID record for Enamul Haque [Opens in a new window]  and
M. Anwar Hossain
Enamul Haque*
Affiliation:
Department of Physics, Mawlana Bhashani Science and Technology University, Santosh, Tangail-1902, Bangladesh
M. Anwar Hossain
Affiliation:
Department of Physics, Mawlana Bhashani Science and Technology University, Santosh, Tangail-1902, Bangladesh
*
a)Address all correspondence to this author. e-mail: enamul.phy15@yahoo.com
Get access

Abstract

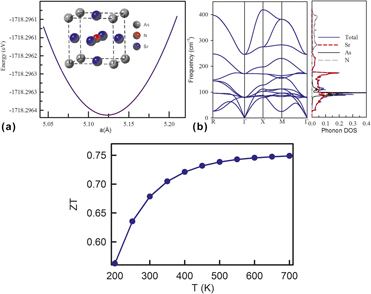
Antiperovskite materials are of high research interest because of their unusual physical properties and technological applications. Here, we report the structural stability and transport properties of Sr3AsN from first-principles study. The calculated equilibrium lattice parameters are in good agreement with the available data. We find that Sr3AsN is mechanically, energetically and dynamically stable at ambient conditions. Our calculated electronic structure indicates that it is a direct band gap semiconductor, with a band gap value ∼1.2 eV. Sr-4d and N-2p orbitals predominantly contribute to the formation of the direct band gap. The calculated Seebeck coefficient of Sr3AsN is high (298 μV/K at 300 K), while the lattice thermal conductivity is comparatively low (1.73 W/m K). The considerable mass difference between Sr, As, and N gives rise to an intense phonon scattering that results in such low lattice thermal conductivity. Our calculated maximum thermoelectric figure of merit (ZT) is 0.75 at 700 K, indicating that it is a potential material for thermoelectric device applications.

Keywords

structural stabilityband gaplattice thermal conductivityeffective massrelaxation time
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 15 , 14 August 2019 , pp. 2635 - 2642
Check for updates
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Tritt, T.M. and Subramanian, M.A.: Thermoelectric materials, phenomena, and applications: A bird’s eye view. MRS Bull. 31, 188 (2006).CrossRefGoogle Scholar
Ioffe, A.: Semiconductor Thermoelements and Thermoelectric Cooling, 1st ed. (Infosearch, London, 1957); p. 99.Google Scholar
Goldsmid, H.J.: Introduction to Thermoelectricity, 1st ed. (Springer, Berlin, 2010); pp. 7–21.CrossRefGoogle Scholar
Saifullah, M. Bilal, Shafiq, M., Khan, B., Aliabad, H.A. Rahnamaye, Asadabadi, S.J., Ahmad, R., and Ahmad, I.: Antiperovskite compounds SbNSr3 and BiNSr3: Potential candidates for thermoelectric renewable energy generators. Phys. Lett. A 379, 206 (2015).Google Scholar
Gäbler, F., Kirchner, M., Schnelle, W., Schwarz, U., Schmitt, M., Rosner, H., and Niewa, R.: (Sr3N)E and (Ba3N)E (E = Sb, Bi): Synthesis, crystal structures, and physical properties. Z. Anorg. Allg. Chem. 630, 2292 (2004).CrossRefGoogle Scholar
Bouhemadou, A., Khenata, R., and Djabi, F.: Structural, elastic, electronic and optical properties of the cubic perovskite BiAlO3. Solid State Sci. 11, 556 (2009).CrossRefGoogle Scholar
Moakafi, M., Khenata, R., Bouhemadou, A., Semari, F., Reshak, A.H., and Rabah, M.: Elastic, electronic and optical properties of cubic antiperovskites SbNCa3 and BiNCa3. Comput. Mater. Sci. 46, 1051 (2009).CrossRefGoogle Scholar
Hsieh, T.H., Liu, J., and Fu, L.: Topological crystalline insulators and Dirac octets in antiperovskites. Phys. Rev. B 90, 81112 (2014).CrossRefGoogle Scholar
Okamoto, Y., Sakamaki, A., and Takenaka, K.: Thermoelectric properties of antiperovskite calcium oxides Ca3PbO and Ca3SnO. J. Appl. Phys. 119, 205106 (2016).CrossRefGoogle Scholar
Miao, N., Xu, B., Bristowe, N.C., Bilc, D.I., Verstraete, M.J., and Ghosez, P.: First-principles study of the thermoelectric properties of SrRuO3. J. Phys. Chem. C 120, 9112 (2016).CrossRefGoogle Scholar
Zhao, L-D., Lo, S-H., Zhang, Y., Sun, H., Tan, G., Uher, C., Wolverton, C., Dravid, V.P., and Kanatzidis, M.G.: Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373 (2014).CrossRefGoogle ScholarPubMed
Heremans, J.P., Jovovic, V., Toberer, E.S., Saramat, A., Kurosaki, K., Charoenphakdee, A., Yamanaka, S., and Snyder, G.J.: Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states. Science 321, 554 (2008).CrossRefGoogle ScholarPubMed
Mahan, G.D.: Good thermoelectrics. Solid State Phys. 51, 81 (1998).CrossRefGoogle Scholar
Beznosikov, B.V.: Predicted nitrides with an antiperovskite structure. J. Struct. Chem. 44, 885 (2003).CrossRefGoogle Scholar
Hichour, M., Khenata, R., Rached, D., Hachemaoui, M., Bouhemadou, A., Reshak, A.H., and Semari, F.: FP-APW+lo study of the elastic, electronic and optical properties for the cubic antiperovskite ANSr3 (A = As, Sb and Bi) under pressure effect. Phys. B 405, 1894 (2010).CrossRefGoogle Scholar
Haddadi, K., Bouhemadou, A., Louail, L., Rahal, F., and Maabed, S.: Prediction study of the structural, elastic and electronic properties of ANSr3 (A = As, Sb, and Bi). Comput. Mater. Sci. 46, 881 (2009).CrossRefGoogle Scholar
Ullah, I., Murtaza, G., Khenata, R., Mahmood, A., Muzzamil, M., Amin, N., and Saleh, M.: Structural and optoelectronic properties of X3ZN (X = Ca, Sr, Ba; Z = Â As, Sb, Bi) anti-perovskite compounds. J. Electron. Mater. 45, 3059 (2016).CrossRefGoogle Scholar
Grimvall, G., Magyari-Köpe, B., Ozolicnš, V., and Persson, K.A.: Lattice instabilities in metallic elements. Rev. Mod. Phys. 84, 945 (2012).CrossRefGoogle Scholar
Wallace, D.C.: Thermodynamics of Crystals (Dover Publications, Inc., Mineola, New York, 1998); pp. 106–180.Google Scholar
Chan, M.K.Y. and Ceder, G.: Efficient band gap prediction for solids. Phys. Rev. Lett. 105, 196403 (2010).CrossRefGoogle ScholarPubMed
Koller, D., Tran, F., and Blaha, P.: Merits and limits of the modified Becke-Johnson exchange potential. Phys. Rev. B 83, 195134 (2011).CrossRefGoogle Scholar
Becke, A.D. and Johnson, E.R.: A simple effective potential for exchange. J. Chem. Phys. 124, 221101 (2006).CrossRefGoogle ScholarPubMed
Mouhat, F. and Coudert, F-X.: Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 90, 224104 (2014).CrossRefGoogle Scholar
Elliott, R.S., Triantafyllidis, N., and Shaw, J.A.: Stability of crystalline solids—I: Continuum and atomic lattice considerations. J. Mech. Phys. Solids 54, 161 (2006).CrossRefGoogle Scholar
Togo, A. and Tanaka, I.: First principles phonon calculations in materials science. Scr. Mater. 108, 1 (2015).CrossRefGoogle Scholar
Li, W. and Mingo, N.: Thermal conductivity of fully filled skutterudites: Role of the filler. Phys. Rev. B 89, 184304 (2014).CrossRefGoogle Scholar
Tran, F. and Blaha, P.: Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 102, 226401 (2009).CrossRefGoogle ScholarPubMed
Koller, D., Tran, F., and Blaha, P.: Improving the modified Becke-Johnson exchange potential. Phys. Rev. B: Condens. Matter Mater. Phys. 85, 1 (2012).CrossRefGoogle Scholar
Engel, E. and Vosko, S.H.: Exact exchange-only potentials and the virial relation as microscopic criteria for generalized gradient approximations. Phys. Rev. B 47, 13164 (1993).CrossRefGoogle ScholarPubMed
Guo, R., Wang, X., Kuang, Y., and Huang, B.: First-principles study of anisotropic thermoelectric transport properties of IV–VI semiconductor compounds SnSe and SnS. Phys. Rev. B 92, 115202 (2015).CrossRefGoogle Scholar
Bardeen, J. and Shockley, W.: Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 80, 72 (1950).CrossRefGoogle Scholar
Hamaguchi, C. and Hamaguchi, C.: Basic Semiconductor Physics (Springer, Berlin, 2001).CrossRefGoogle Scholar
Xi, J., Long, M., Tang, L., Wang, D., and Shuai, Z.: First-principles prediction of charge mobility in carbon and organic nanomaterials. Nanoscale 4, 4348 (2012).CrossRefGoogle ScholarPubMed
Haque, E. and Hossain, M.A.: Origin of ultra-low lattice thermal conductivity in Cs2 BiAgX6 (X = Cl, Br) and its impact on thermoelectric performance. J. Alloys Compd. 748, 63 (2018).CrossRefGoogle Scholar
Xing, G., Sun, J., Li, Y., Fan, X., Zheng, W., and Singh, D.J.: Electronic fitness function for screening semiconductors as thermoelectric materials. Phys. Rev. Mater. 1, 65405 (2017).CrossRefGoogle Scholar
Ochi, M. and Kuroki, K.: Comparative first-principles study of antiperovskite oxides and nitrides as thermoelectric material: Multiple Dirac cones, low-dimensional band dispersion, and high valley degeneracy. arXiv Prepr. arXiv1902.03424, 2019.Google Scholar
Perdew, J.P., Burke, K., and Ernzerhof, M.: Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).CrossRefGoogle ScholarPubMed
Perdew, J.P., Ruzsinszky, A., Csonka, G.I., Vydrov, O.A., Scuseria, G.E., Constantin, L.A., Zhou, X., and Burke, K.: Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008).CrossRefGoogle ScholarPubMed
Blaha, P., Schwarz, K., Madsen, G.K.H., Kvasnicka, D., and Luitz, J.: WIEN2k. An augmented plane wave + local orbitals program. Calc. Cryst. Prop. (2001).Google Scholar
Madsen, G.K.H. and Singh, D.J.: BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67 (2006).CrossRefGoogle Scholar
Esfarjani, K. and Stokes, H.T.: Method to extract anharmonic force constants from first principles calculations. Phys. Rev. B 77, 144112 (2008).CrossRefGoogle Scholar
Parlinski, K., Li, Z.Q., and Kawazoe, Y.: First-principles determination of the soft mode in cubic ZrO2. Phys. Rev. Lett. 78, 4063 (1997).CrossRefGoogle Scholar
Togo, A., Chaput, L., and Tanaka, I.: Distributions of phonon lifetimes in Brillouin zones. Phys. Rev. B 91, 94306 (2015).CrossRefGoogle Scholar
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., Ceresoli, D., Chiarotti, G.L., Cococcioni, M., Dabo, I., Dal Corso, A., de Gironcoli, S., Fabris, S., Fratesi, G., Gebauer, R., Gerstmann, U., Gougoussis, C., Kokalj, A., Lazzeri, M., Martin-Samos, L., Marzari, N., Mauri, F., Mazzarello, R., Paolini, S., Pasquarello, A., Paulatto, L., Sbraccia, C., Scandolo, S., Sclauzero, G., Seitsonen, A.P., Smogunov, A., Umari, P., and Wentzcovitch, R.M.: QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 21, 395502 (2009).Google ScholarPubMed
Garrity, K.F.: First-principles search for n-type oxide, nitride, and sulfide thermoelectrics. Phys. Rev. B 94, 45122 (2016).CrossRefGoogle ScholarPubMed
Guo, S-D.: Biaxial strain tuned thermoelectric properties in monolayer PtSe2. J. Mater. Chem. C 4, 9366 (2016).CrossRefGoogle Scholar
Seko, A., Togo, A., Hayashi, H., Tsuda, K., Chaput, L., and Tanaka, I.: Prediction of low-thermal-conductivity compounds with first-principles anharmonic lattice-dynamics calculations and Bayesian optimization. Phys. Rev. Lett. 115, 205901 (2015).CrossRefGoogle ScholarPubMed
Joshi, H., Rai, D.P., Deligoz, E., Ozisik, H.B., and Thapa, R.K.: The electronic and thermoelectric properties of a d2/d0 type tetragonal half-Heusler compound, HfSiSb: A FP-LAPW method. Mater. Res. Express 4, 105506 (2017).CrossRefGoogle Scholar
Whalley, L.D., Skelton, J.M., Frost, J.M., and Walsh, A.: Phonon anharmonicity, lifetimes, and thermal transport in CH3NH3PbI3 from many-body perturbation theory. Phys. Rev. B 94, 220301 (2016).CrossRefGoogle Scholar
Supplementary material: File

Haque and Hossain supplementary material

Haque and Hossain supplementary material 1

Download Haque and Hossain supplementary material(File)
File 57.6 KB