Article contents
Identifying rhenium substitute candidate multiprincipal-element alloys from electronic structure and thermodynamic criteria
Published online by Cambridge University Press: 10 June 2019
Abstract
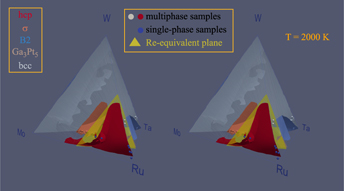
While rhenium has proven to be an ideal material in fast-cycling high-temperature applications such as rocket nozzles, its prohibitive cost limits its continued use and motivates a search for viable cost-effective substitutes. We show that a simple design principle that trades off average valence electron count and cost considerations proves helpful in identifying a promising pool of candidate substitute alloys: The Mo–Ru–Ta–W quaternary system. We demonstrate how this picture can be combined with a computational thermodynamic model of phase stability, based on high-throughput ab initio calculations, to further narrow down the search and deliver alloys that maintain rhenium’s desirable hcp crystal structure. This thermodynamic model is validated with comparisons to known binary phase diagram sections and corroborated by experimental synthesis and structural characterization demonstrating multiprinciple-element hcp solid-solution samples selected from a promising composition range.
Information
- Type
- Invited Paper
- Information
- Journal of Materials Research , Volume 34 , Issue 19: Focus Issue: Thermodynamics of Complex Solids , 14 October 2019 , pp. 3296 - 3304
- Copyright
- Copyright © Materials Research Society 2019
Footnotes
This author was an editor of this journal during the review and decision stage. For the JMR policy on review and publication of manuscripts authored by editors, please refer to http://www.mrs.org/editor-manuscripts/.
References
- 8
- Cited by

