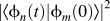Approaching the quantum limit for nanoplasmonics

Abstract

The character of optical excitations in nanoscale and atomic-scale materials is often strongly mixed, having contributions from both single-particle transitions and collective, plasmon-like response. This complicates the quantum description of these excitations, because there is no clear way to define their quantization. To move toward a quantum theory for these optical excitations, they must first be characterized so that single-particle-like and collective, plasmon-like excitations can be identified. We show that time-dependent density functional theory can be used to make that characterization if both the charge densities induced by the excitation and the transitions that make up the excitation are analyzed. Density functional theory predicts that single-particle-like and collective excitations can coexist. Exact calculations for small nanosystems predict that single-particle excitations evolve into collective excitations as the electron–electron interaction is turned on with no indication that they coexist. These different predictions present a challenge that must be resolved to develop an understanding for quantum excitations in nanoplasmonic materials.

I. INTRODUCTION

Plasmons are wavelike excitations of oscillating charge density that arise in metals, such as gold and silver, where there is a high density of free conduction electrons.¹ Plasmons can occur in the bulk, at a surface or at an interface between the metal and a dielectric or air. They also occur in other systems with mobile charges, such as long chain molecules,^2,3 atomic chains on surfaces,^4,5 carbon nanotubes,⁶ doped graphene,⁷ and other complex molecules.⁸ They can be excited by passing charge or, more importantly, by optical and infrared (IR) fields in structured materials, such as metal waveguides, gratings, and nanoparticles, just as radio waves drive current in an antenna. The collective participation of a large number of charges in these plasmonic excitations gives them an intense optical response. However, rapid damping via scattering among these carriers contributes to femtosecond lifetimes and broad resonances.

The intense optical response of surface plasmons in metal nanoparticles has been exploited for a thousand years to provide the beautiful colors of glasses. Over the last 60 years, plasmonic excitations have been studied extensively in a wide range of bulk materials.⁹ In the last two decades, the interest in plasmonics has exploded. With the advent of nanotechnology, a variety of fabrication and chemical growth techniques have been developed to tailor the makeup, structure, size, and shape of nanomaterials for plasmonics, tune the resonance frequencies to desired optical and IR wave lengths, and enhance local fields strongly at desired locations. In particular, using nanomaterials for plasmonics, also referred to as nanoplasmonics, to confine light near surfaces or in nanoparticle gaps to nanoscale volumes much smaller than the diffraction limit has opened a wide range of new applications for nanooptics. Nanoplasmonics has enabled bio and chemical sensing at the few-molecule level by using metal nanoparticles as optical nanoantennas to enhance light coupling to individual emitters.^10,11 Nanoplasmonics provides metamaterials with novel response such as negative refraction.^12–14 Nanoplasmonics can be used to enhance light conversion for solar energy collection,¹⁵ nanoheating,¹⁶ and nanoscale cancer diagnostics and therapies.¹⁷ This wide range of applications for nanooptics has driven the recent explosive growth in the interest in nanoplasmonics.

Surface plasmons are hybrid excitations that take on the character of the optical field induced by the plasmon and the oscillating charge. Classical optical physics (Maxwell's equations and the material's bulk dielectric function) usually provides an excellent description of plasmonic response and has been the workhorse for describing many of the nanoplasmonic effects now being exploited. However, quantum effects in optics have been known for years and have spawned the field of quantum optics. Whether, when or how quantum effects should be important for nanoplasmons has not been obvious—in particular because, unlike photons, plasmons decohere and decay in femtoseconds due to strong electron–electron scattering among the many conduction electrons participating in the plasmon, leaving little time for quantum effects to play out.

Recently, however, it has become apparent that quantum effects can play a significant role in plasmonics, despite rapid plasmon decay and decoherence.^18,19 Quantum plasmonic effects can arise from the quantum character of the participating electrons. For metal nanoparticle antennas with nanometer gaps—the antennas that provide the largest field enhancement and smallest mode volumes and are therefore most desirable for nanoscale sensing—quantum tunneling of charge across the gap distorts the surface plasmons, smearing out the fields, and limiting the useful enhancement.²⁰ In nanoparticles so small that size quantization becomes important, the broadband response of a classical plasmon breaks up into a series of discrete excitations. Some are still surface plasmons, others are single-particle-like excitations and others have mixed character.^21,22

Quantum effects should also appear because plasmons are photonic. In the last decade, a variety of quantum optics experiments have shown that plasmons can behave like photons in the quantum limit with quantum coherence surviving in the plasmonic structures. Entangled photons can be transported by surface plasmons,²³ energy-time entanglement of photon pairs can survive a photon-plasmon-photon conversion,²⁴ and quadrature squeezing has been achieved.²⁵ Most recently, individual plasmons have been coupled by a 50/50 beam splitter in a Hong Ou Mandel interference experiment.²⁶ Two interfering plasmons are seen to arrive only at the same detector, a clear signature of quantum interference at the beam splitter.^27,28 However, in many of these experiments, the plasmons are nearly photonic and it is unclear that one needs to invoke quantized matter excitations to understand the quantum response. In any case, these experiments do raise fundamental questions about how quantum information and resources, such as entanglement, can be transmitted via lossy plasmonic channels via quantum/classical interfaces. These are the questions that arise for all photonic systems but are more challenging for plasmonic channels which have larger losses. Furthermore, quantum plasmonics offers the new twist of intense local fields and small mode volumes that provide strong light-matter coupling and strong nonlinear response even for weak input fields which are difficult to achieve with light alone.

Plasmonic nanoantennas and nanoguides could also provide nanoscale pathways for directing optical communication between local quantum emitters. Such plasmonic guiding would extend optical quantum communication, now done with photonic structures and optical cavities, to the nanoscale, with orders of magnitude better spatial resolution and with addressing that dramatically beats the diffraction limit for optics, but only if the quantum character of the information is preserved while being carried by the plasmons. A prototypical realization for this nanoscale quantum information transfer uses hybrid systems of metallic nanoparticles (MNP) linked to quantum emitters such, as atoms, molecules, and quantum dots with plasmons in MNPs moving qubits from emitter to emitter. When the nanohybrid is driven by a weak light field, a classical description of the nanohybrid is sufficient and the MNP can enhance or quench the response of the emitter.^11,29,30 When the nanohybrid is strongly driven by a light field, the quantum coherent coupling between the light and the emitter becomes important and the dynamics of the nanohybrid can be dramatically different.^31–45 Descriptions of strongly driven nanohybrids with the emitter treated quantum mechanically and the MNP response treated classically predict a nonlinear Fano effect, bistability, and induced transparency.^31–38 A variety of applications have been proposed that exploit these effects,^46–48 suggesting new building blocks for metamaterials with properties very different from those of the constituents of the nanohybrid. Recently, these nanohybrids have been described with a full quantum mechanical treatment with quantized nanoparticle plasmons.^39–45 Strong coupling and the nonlinear Fano effects also appear. Qubit entanglement, superabsorption, and cloaking are possible. However, some of the exciting predictions of the quantum/classical models, such as the bistability, disappear in the fully quantum treatment.^39,45

Controlled fabrication of these nanohybrids is still a daunting experimental challenge. To assess the potential of these nanohybrids as new building blocks for novel metamaterials, it becomes essential that one know when and how quantum theories must be used to predict their properties. To date, quantized plasmons in nanohybrids have been introduced by directly quantizing the optical near-fields induced around the nanoparticles by the classical plasmonic modes, just as the classical optical modes in a cavity are quantized,^39–41 and broadening each quantized mode by the mode lifetime to reproduce the classical response. Quantized plasmons have also been described by introducing a collection of local oscillators with different frequencies to reproduce the broad classical response of the plasmons.^42–45

These approaches start from the photonic character of the plasmonic excitations to implement the quantization. However, the material, electronic character of the plasmonic excitations should also be accounted for. For bulk systems with translational invariance, the plasmons are typically quantized, as done for lattice vibrations, by quantizing the charge density oscillations in the system.⁴⁹ The same approach can be used for spherical nanoparticles.⁵⁰ However, these approaches face significant challenges for nanoscale systems with both single-particle-like and plasmonic excitations.

Single-particle and plasmonic excitations both play key roles in nanooptics. Single-particle excitations provide discrete energies ideal for use as emitters, lasers, and detectors. Plasmons with the broad, intense response are ideal for enhancing light–matter interaction. However, in small systems the single-particle-like transitions can be strongly mixed with collective excitations with many participating electrons. It need not be clear which excitations should be quantized, whether they are fermions or bosons, or even which excitations are plasmonic. The effects of size quantization in small systems further distort the character of the excitations and mix the states.^2,21,22 Resolving these issues for small systems is also complicated by the number of electrons involved. The systems are neither many-electron systems that can be treated with bulk many-body theory, nor are they simple few-electron systems. As a first step, a clear characterization of the excitations must be made and the single-particle and collective excitations be distinguished. One can then address the issue of how these excitations should be quantized, whether they are fermionic or bosonic, and whether excitations are independent or strongly coupled to each other. In this study, we address this first step and show how one can distinguish the different types of optical excitations in nanoscale systems.

In the following, we discuss two different theoretical approaches and two different nanoscale systems. The goal is to show how single-particle and plasmonic excitations can be identified and distinguished. In Sec. II, we outline the two theoretical approaches. We use density functional theory to investigate small spherical MNPs and we exploit exact calculations to study the excitations of linear chains of atoms. Such exact calculations are possible for short chains with only a few atoms. The exact calculations provide the possibility of investigating how quantization appears without having to impose it. In Sec. III and IV, we describe, respectively, the results for MNPs and for short linear chains. We end with discussion and conclusions in Sec. V.

II. THEORETICAL DETAILS

We consider two approaches to better understand the nature of optical excitations in nanoscale systems. We first use real-space, real-time time-dependent density functional theory (TDDFT) to obtain a quantum description of MNPs.⁵¹ DFT theory reduces the full many-body problem to a calculation where the electronic charge density is the key material quantity that defines material properties. In DFT, a single-electron Schrodinger-like equation is solved for the Kohn–Sham states that define the electronic charge density. Although a single-electron-like equation is solved, each electron interacts self-consistently with the other electrons via the Hartree interaction, which is determined from the total electronic charge density, and via the exchange and correlation potentials, also defined in terms of the electronic charge density.⁵¹ Here, we treat the MNPs as Au jellium nanospheres with a uniform positive charge background to model the ions.^21,22 The jellium model has been studied extensively.^52,53 Most recently, the jellium background has been replaced by the lattice of ionic cores to account for atomistic effects as well.⁵⁴ In this study, our goal is to show how to characterize the optical excitations and to distinguish single-particle and collective excitations. The simpler jellium model is sufficient for this purpose. We consider the limit of small MNPs where size quantization and the finite number of electrons play a key role and show how these effects evolve as the nanoparticle size increases.

The TDDFT calculations proceed in three steps. First, DFT is used to determine the electronic ground state of the jellium MNP.⁵¹ The Schrodinger-like equation is solved to determine the single-particle-like Kohn–Sham orbitals (${\phi _i}$, with orbital energy ε_i) that are occupied for ε_i less than the Fermi level ε_F to determine the ground-state electron charge density. Then, TDDFT is used to determine the response of the MNP to an instantaneous electromagnetic delta-impulse by evolving each occupied Kohn–Sham orbital in time after the impulse. The time-dependent dipole moment of the MNP is determined. Its Fourier transform gives the frequency-dependent response of the system. A typical spectrum for a 100-electron MNP is shown in Fig. 1. The width of each peak is determined by the length of the time evolution. Once the excitation frequencies are determined from the spectrum, the TDDFT time evolution is repeated for electromagnetic driving fields at the excitation frequencies identified from the spectrum. This allows us to explicitly investigate the spatial character of each excitation as it evolves, define which single-electron transitions between Kohn–Sham orbitals contribute to the excitation, and determine how these contributions evolve in time. As we will demonstrate, this information allows us to distinguish single-particle and plasmonic (i.e., collective) excitations. However, TDDFT does not describe how these material excitations should be quantized, nor does it describe whether the excitations are fermions or bosons, or whether multiple plasmonic excitations are independent, like bosons, or coupled.

FIG. 1. Optical response of spherical Au MNPs. (a) Frequency-dependent response for a 100-electron Au MNP. Frequency on the horizontal axis is displayed in units of the classical surface plasmon frequency. (b) Time-dependent induced charge density for the classical surface plasmon [ω = 0.90ω_sp, as indicated by the circle in (a)] of a 100-electron MNP. The color shows the induced charge along the axis (x) parallel to the driving field through the center of the MNP. R is the MNP radius. The bottom (blue) line shows the phase of the driving electric field. The solid line with circles is the ground-state electron density as a function of position x. The ground-state electron density is found in a DFT calculation and then used as the starting density for the TDDFT time simulations. The scale for the ground-state electron density, normalized by the density of the jellium background, is shown at the top. T is the period of the driving field. (c) Time-dependent induced charge density for the quantum core plasmon (ω = 0.74ω_sp) of a 100-electron MNP. (d) Frequency-dependent response for a 600-electron Au MNP.

To address these quantization issues without imposing the form of the quantization as constraints the theory must obey, we need a full quantum mechanical theory of these excitations that finds the actual many-body eigenstates of the system rather than just the charge density, as in DFT. With the full eigenstates, one can determine how they are quantized. To gain some insight into what such a theory might reveal, we have studied some simple models for interacting electrons in small nanoscale systems. The goal is to study systems small enough that they can be analyzed exactly. This limits the models to systems with a small number of electrons. Here, we study a linear chain of atoms, with electrons hopping from atom to atom along the chain. Such a model describes atomic chains on surfaces^4,5 and linear molecules.^2,3 Most importantly it should provide insight on how plasmonic excitations arise in these systems.

Here, we consider a single-band model for the linear chain of atoms with one electronic state on each atomic site and short range, next-neighbor hopping t between atoms. If there are N _s sites in the chain and m _e electrons in the system, then there are $\left( {\matrix{ {{\it N}_{\rm{s}} } \cr {{\it m}_{\rm{e}} } \cr } } \right) = {{{\it N}_{\rm{s}} !} \over {{\it m}_{\rm{e}} !\left( {{\it N}_{\rm{s}} - {\it m}_{\rm{e}} } \right)!}}$ many-electron states in the system. In a charge neutral system, each site has a nuclear charge Z = m _e/N _s. An electron at site i interacts with the nuclear charge Z at site j via the attractive Coulomb interaction

(1)$${V_{{\rm{nuc}}}}\left( {i,j} \right) = {{ - {\lambda _{{\rm{nuc}}}}Z} \over {\left( {\left| {i - j} \right| + {\xi _{{\rm{nuc}}}}} \right)}}\quad ,$$

where λ_nuc is a scale factor that includes any dielectric screening and the length scale for the site separation and ξ_nuc is a cutoff that accounts for the orbital spread of the electron orbital on a site. An electron at site i interacts with an electron at site j via the repulsive Coulomb interaction

(2)$${V_{{\rm{ee}}}}\left( {i,j} \right) = {{{\lambda _{{\rm{ee}}}}} \over {\left( {\left| {i - j} \right| + {\xi _{{\rm{ee}}}}} \right)}}\quad ,$$

where λ_ee is the scale factor that includes any dielectric screening and the length scale for the site separation and ξ_ee is the cutoff that accounts for the spread of the electron orbital on a site. The effects of electron–electron interaction are balanced by the electron–nuclear interaction when λ_ee = λ_nuc. Optical response in this model is proportional to the dipole moment of the electrons along the chain.

All electronic states for this model can be easily determined by standard numerical diagonalization techniques when the system has less than ten thousand states. Here, we consider a half-filled band of spinless electrons (m _e = N _s/2). In that case, we can consider chains with up to 16–20 atoms. For longer chains or when electron spin is included, it becomes impractical to determine all the many-electron states. Instead, one must use diagonalization techniques that find limited parts of the spectrum. Here, we focus on the smaller chains where all excitations can be found and analyzed. This allows us to investigate the characteristics that will distinguish plasmonic-like, collective excitations from single-particle excitations. Developing this insight will allows us to study larger systems where we must start with educated choices about which selected parts of the spectrum to investigate to find the plasmon-like excitations.

III. DENSITY FUNCTIONAL THEORY OF METAL NANOPARTICLES

Collective/plasmonic excitations can be strongly mixed with single-particle excitations in nanoscale systems, making it difficult to characterize the excitations. We consider a 2-nm-diameter Au MNP with 100 electrons to show how the character of its excitations can be defined.^21,22 Figure 1(a) shows the spectral response of the 100-electron gold MNP found using TDDFT and the jellium model. The spectrum has well separated, narrow peaks, several with large oscillator strengths, and the rest substantially weaker. There are no losses in the calculation so the width of each peak is determined by the length of the time simulation. The time evolution is long enough to ensure that peaks are resolved and that each resonance frequency can be accurately determined. Typically, the simulations are run for tens of periods of the driving field. This is comparable to the plasmon lifetime, although the sharpest spectra shown here would be broadened by typical losses and inhomogeneous effects. To reveal the nature of each excitation, we drive the MNP at the excitation resonance frequency. The time evolution of the induced charge density when driven at the two indicated frequencies is shown in Figs. 1(b) and 1(c). The induced charge density oscillation for the most prominent peak is localized mostly at the MNP surface, behaving as one would expect for the classical surface plasmon. There is structure in the induced charge density near the surface that arises due to the quantum confinement. The excitation illustrated in Fig. 1(c) also shows an oscillating induced charge density, but it is localized to the core of the MNP. We have previously referred to this as a quantum core plasmon, because it is a plasmon-like internal excitation that arises because of confinement effects. The dependence on size is shown by comparing the response of a 600-electron MNP [Fig. 1(d)] with the response for the 100-electron MNP. In the larger MNP, the response of the core plasmon is much weaker and not easily identifiable. For the 100-electron MNP, there are two additional strong excitations between the core and surface plasmons that have mixed character of both the core and surface plasmons. In addition, there are a large number of weak resonances, especially for the smaller MNP. These resonances are sensitive to the boundary conditions used to define the computational region for the DFT. This indicates that these excitations have higher-energy electrons that can escape the MNP and are sensitive to the details of the computational boundary. The energy and spatial character of the classical surface and quantum core plasmons do not depend on the boundary conditions, indicating that these are internal excitations of the MNP.

It is tempting to conclude that this analysis has determined that the prominent excitations are plasmonic. However, further analysis will show that the core plasmon is really predominately single-particle-like. This is already hinted at by the size dependence. The core plasmon is much weaker than the surface plasmon in the larger dot, indicating that the strength of the core plasmon does not scale with the size of the system, as it would if it were a plasmon-like, collective, many-electron excitation.

To get a clearer picture of which excitations are collective and which are single-particle-like, one must determine which single-electron transitions contribute to each excitation and how these contributions evolve as the MNP is driven on resonance. In a time simulation of a driven MNP, the MNP starts at t = 0 in its DFT ground state with the DFT Kohn–Sham orbitals for ε_i < ε_F occupied. These occupied orbitals change in time when the driving field is applied for t > 0. The projection of the time-evolving occupied orbital, ${\phi _i}\left( t \right)$, onto its initial, t = 0, orbital gives the probability ${\left| {\left\langle {{\phi _i}\left( t \right)} \right|\left. {{\phi _i}\left( 0 \right)} \right\rangle } \right|^2}$ that ith state has evolved without changing its initial state. The probability that the state undergoes a transition to another state j is given by the off-diagonal projection ${\left| {\left\langle {{\phi _i}\left( t \right)} \right|\left. {{\phi _j}\left( 0 \right)} \right\rangle } \right|^2}$. Many of these single-electron transitions could contribute to an excitation. How they contribute will define the character of the excitation. Figure 2 shows these transition probabilities at one time when the 100-electron MNP is driven continuously at the surface plasmon resonance. The off-diagonal transitions are small, in the 10⁻⁴ range. The decrease in the probabilities to remain unchanged in the ground-state Kohn–Sham state is in the same range. The total induced charge density is small and the response is well within the linear regime. The orbital symmetries of the states in the transitions are indicated on the axes in Fig. 2. The Fermi level is in the 2f level. As expected for optical excitation, the allowed transitions have a change of orbital angular momentum of ±1. Four types of transitions are highlighted. Strong transitions from occupied states just below the Fermi level to empty states just above the Fermi level have the appropriate change in angular momentum. However, the change in energy due to these single-electron transitions is much smaller than the excitation energy, indicating that these transitions must contribute collectively to the excitation. As the total occupation of the ground-state Fermi sea is depleted by the driving field, a second class of transitions between states inside the Fermi sea develops and agitates the Fermi sea. At the same time, charge accumulates above the ground-state Fermi sea and a third class of transitions between states above the Fermi level develops. These two classes of transitions that arise because the ground-state Fermi sea is depleted also have energies well below the excitation energy and must contribute collectively to the excitation. Finally, a fourth class of transitions couples states well below the Fermi level to states well above the Fermi level. For these transitions, the energy changes are comparable to the excitation energy indicating that these transitions add single-particle-like character to the excitation. These are transitions that can also contribute to the hot electron generation mentioned previously.

FIG. 2. Projections ${\left| {\left\langle {{\phi _n}\left( t \right)} \right|\left. {{\phi _m}\left( 0 \right)} \right\rangle } \right|^2}$ of time-evolved Kohn–Sham states for the classical surface plasmon onto the ground-state Kohn–Sham states in the 100-electron MNP. The snapshot is shown for an arbitrarily chosen time. The circles highlight the four classes of transitions discussed in the text.

The transition probabilities for collective and single-particle contributions have distinctly different time dependences. For the class of transitions that makes single-particle-like contributions, the transition probabilities increase monotonically as the MNP is driven for the time-scale of the simulations. This monotonic increase is expected from Fermi's golden rule for single-particle transitions weakly driven well below saturation. For the three classes of transitions that contribute collectively, the transition probabilities initially increase on average as the MNP is driven, but this average increase is strongly sinusoidally modulated at the resonance frequency and by low frequency beating. These differences in the time dependence for the single-particle and collective transitions are also apparent in the time dependence of the occupation of each ground-state level.²² Levels just below the Fermi level deplete and then refill. This oscillation in level occupation occurs at the resonance frequency. In addition, charge accumulates in states just above the ground-state Fermi level and then empties from those states, in phase with the depletion and refilling of the states below the Fermi level. This collective sloshing of charge back and forth from just below the Fermi level to just above the Fermi level is the hallmark of a plasmon-like excitation. At the same time, single-particle-like transitions from states well below the Fermi level to well above the Fermi level deplete the levels well inside the Fermi sea monotonically, leading to an inversion of charge well above the Fermi level. For the 100-electron MNP, all four classes of transitions contribute to each resonance because the resonances are strongly mixed. Nonetheless, the surface plasmon resonance is dominated by transitions that slosh charge back and forth from just below to just about the Fermi level. In contrast, the resonance labeled a quantum core plasmon is dominated by the transitions that invert the charge from well below to well above the Fermi level. From this analysis, it becomes clear that the quantum core “plasmon” is predominantly a single-particle excitation.

The spatial distribution of induced charge associated with each class of transitions further defines the character of the excitations. The sloshing transitions induce charge density oscillations at the surface. Transitions between states both inside the Fermi sea or both above the Fermi sea make little contribution to the induced charge oscillation of an excitation. The single-particle-like transitions contribute to the induced charge density oscillations inside the MNP, either to structure the charge density oscillation near the surface or to define the oscillations deeper inside the MNP that characterize the core plasmon.

The TDDFT analysis shows that the single-particle and plasmonic transitions in nanoscale systems can be identified and distinguished even though they can be strongly mixed. To determine the nature of an excitation, both its time-dependent induced charge oscillation and the time dependence of the transitions that contribute to it must be characterized. Single-particle-like excitations have contributions from single-particle transitions with energy changes comparable to the excitation energy. These contributions increase monotonically with time and occur mostly inside the MNP. The collective surface plasmon-like excitations arise from charge sloshing back and forth from just below to just above the Fermi level. Many low-energy transitions contribute collectively to this excitation.

IV. ONE-DIMENSIONAL CHAIN MODELS FOR NANOPLASMONICS

The TDDFT analysis says nothing about how to quantize the excitations in nanoscale and atomic-scale systems, nothing about whether the excitations are bosonic or fermionic, and nothing about whether the excitations are independent or coupled nonlinearly. Exact solutions possible for small systems provide a framework to address these questions. However, the first step in this approach is still to see if the excitations have well-defined characteristics that can distinguish them as plasmonic or single-particle. In this section, we discuss initial exact results for short linear chains of atoms to see what insight can be gained. We only consider here chains with fewer than 20 atoms where exact results for the entire spectrum can be obtained. This allows us to examine the full spectrum to find the signs of plasmonic excitations.

As we have already discussed, excitations in nanoscale systems can be strongly mixed with both single-particle and plasmonic character. Here, we follow an approach recently developed by Bernadotte et al.² to identify single-particle and plasmonic excitations in TDDFT calculations for short linear molecules. They found that many excitations could be identified as single-particle or plasmonic. To make this identification, they varied the scale of the Coulomb interaction in the TDDFT using the same scale factor λ_ee that we use to define the electron–electron repulsion in our model. In their TDDFT calculations, single-particle-like excitations had excitation energies that depended only weakly on the Coulomb scale factor λ_ee. In contrast, other excitations had excitation energies that scaled with the square root of the Coulomb interaction strength. This square root scaling is expected for plasmonic excitations. When these excitations crossed, they had mixed character.

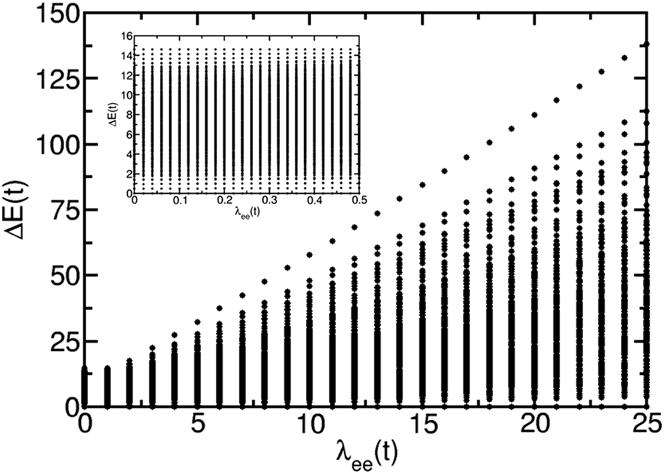
We have followed this approach for our exact calculations. Here, we illustrate the results by discussing chains with 12 atoms and 6 electrons. This corresponds to a half-filled band of spinless electrons and should have metallic behavior. The full excitation spectrum, with nearly a thousand states, is shown as a function of λ_ee in Fig. 3. All excitation energies are shown relative to the ground-state energy. Qualitatively similar spectra are obtained for eight-atom chains with 4 electrons and 70 excitations and for 16-atom chains with 8 electrons and ten thousand excitations. The spectra for different chain lengths have a similar energy span. The main difference is the density of states. At λ_ee = 0, there is no electron–electron repulsion and no collective response. All excitations are single or multiple independent-electron excitations. As λ_ee increases, the electron–electron interaction is turned on, the excitations become correlated and collective response is possible.

FIG. 3. The spectra of a 12 atom, 6 electron linear atomic chain as a function of the electron–electron interaction strength λ_ee. The excitation energies ΔE are shown relative to the ground-state energy. The inset shows spectra for small λ_ee.

The inset in Fig. 3 shows the excitation spectra for λ_ee < 0.5t, where the electron–electron repulsion is comparable to the hopping. A few low-energy and high-energy excitations are well separated from the quasicontinuum of excitations at intermediate energies. At low energies, these excitations correspond to single-electron excitations in a short chain. The quantum confinement of a finite chain length ensures that the single-electron states have discrete energies. At high energies, the discrete excitations are those formed by removing a single-electron excitation from the fully excited state. Figure 4(a) shows a blowup of the low-energy spectra. The excitation energies increase weakly as the electron–electron repulsion is added. The excitation energies for a few of the states increase faster than others. However, there is no clear separation of states, as predicted by TDDFT, into a set of single-particle states which are nearly independent of λ_ee and another set of states with excitation energies that scale as the square root of λ_ee. An analysis of the low-energy excitations shows that they are single independent-electron excitations. In this range of λ_ee, interaction is too weak to have much effect.

FIG. 4. The low-energy spectra of a 12 atom, 6 electron linear atomic chain as a function of the electron–electron interaction strength λ_ee for (a) weak electron–electron interaction and (b) stronger interaction where collective effects develop. The metallic and Wigner crystal regimes and the regimes of weak and strong Coulomb effects are indicated.

This weak dependence on λ_ee might seem counterintuitive because the electron–electron repulsion is comparable to the hopping. However, the full Coulomb interaction includes both the electron–electron repulsion which leads to collective response and the electron–nucleus attraction which contributes to the independent single-electron energies. Because the chains are chosen to be charge neutral, these interactions compensate each other and the net Coulomb interaction is weak. The spectra for λ_ee increasing up to 25t are shown in Fig. 3. The low-energy excitations for this range of λ_ee are shown in Fig. 4(b). For low λ_ee, the ground-state electron density is uniform along the chain, as would be expected for a metallic state. For very large λ_ee (λ_ee ≈ 25t), the first excited state and the ground state become degenerate. For these λ_ee, the ground-state electron density becomes localized to every other site, as would be expected for a Wigner crystal where the electrons separate and localize into an array due to their mutual repulsion. For a chain with an even number of sites, there are two ways to realize this ground-state density and the ground state becomes doubly degenerate. This suggests that metallic behavior extends up to λ_ee ≈ 25t and the onset of Wigner crystallization. In addition, the highest two excitations become degenerate for λ_ee > 1.5t. The highest energy state becomes fully localized to one half of the chain. Because there are two ways for this to happen, the highest excitation becomes doubly degenerate for λ_ee > 1.5t. For smaller λ_ee, even the highest excitation has a uniform electron density along the chain. These results suggest that strong collective response begins to appear for λ_ee > 1.5t but metallic behavior persists until λ_ee ≈ 25t. These regimes are indicated in Fig. 4. In this range of λ_ee, the low-energy excitations remain well separated from the quasicontinuum and show a clear strong linear dependence on λ_ee. An analysis of these states shows that they are formed from many single and multiple independent-electron states, indicating a strong collective character.

To better identify the optically active single-particle-like and plasmonic/collective excitations, we eliminate from the spectra all excitations that are dipole forbidden. This eliminates all excitations that have the same parity as the ground state and eliminates all excitations made up only from independent-electron states with multiple-electron excitations. This dramatically reduces the density of states in the spectra, as shown in Fig. 5. The largest (blue) circles indicate excitations with the largest oscillator strength. Circles of smaller size (respectively green, red, and gray) have oscillator strengths reduced by one order of magnitude for each size step. The smallest (black) dots indicate all other excitations with finite oscillator strength.

FIG. 5. Optically active excitations in the low-energy spectra of a 12 atom, 6 electron linear atomic chain as a function of the electron–electron interaction strength λ_ee for (a) weak electron–electron interaction and (b) stronger interaction where collective effects develop. The largest (blue) circles indicate excitations with the largest oscillator strength. Circles of smaller size (respectively green, red, and gray) have oscillator strengths reduced by one order of magnitude for each size step. The smallest (black) dots indicate all other excitations with finite oscillator strength.

At λ_ee = 0, only the single-electron excitations are optically active. They occur for excitation energies less than 4t. In the low interaction regime for 0 < λ_ee < 0.5t, these single-particle-like excitations lose oscillator strength as λ_ee increases while higher-energy excitations above the single-electron transitions become optically active. Several of these higher-energy states in the quasicontinuum have higher oscillator strength than nearby states, suggesting that they might be plasmonic/collective states. However, the character of these states changes rapidly as λ_ee increases because of multiple level crossings and strong mixing with the other nearby states in the high density of states. These higher-energy regions in the spectra with strong oscillator strength might correspond to plasmonic-like resonances but they will be short lived. As λ_ee increases further and correlated response becomes important [Fig. 5(b)], the low-energy excitations which are single-particle-like for λ_ee < 0.5t become correlated, collective excitations made from many single- and multiple-electron transitions. The excitation energies increase linearly with λ_ee both at small λ_ee and at large λ_ee with a crossover at intermediate λ_ee. At higher λ_ee, these appear to be plasmon-like collective excitations. There is no indication that collective and single-particle-like excitations can both be present in the spectra at the same λ_ee as predicted by TDDFT.

The predictions of the exact calculations are in striking contrast to the TDDFT predictions for linear chains.² TDDFT predicts that single-particle-like and collective/plasmonic excitations can coexist at the same λ_ee. Excitation energies for single-particle excitations vary weakly with λ_ee. The TDDFT² also predicts that plasmonic excitation energies have a square root dependence on λ_ee. The exact calculations presented here show that the single-particle-like excitations evolve into the collective excitations as λ_ee increases with a crossover region at intermediate λ_ee. At low and high λ_ee the excitation energies depend linearly on λ_ee. There is no indication that well-defined single-particle-like excitations and collective, plasmon-like excitations coexist at the same interaction strength. These different predictions clearly present a challenge that must be resolved to develop an understanding for quantum excitations in these systems.

V. CONCLUSIONS

There is an increasing demand for nanomaterials that can be used for quantum information, cryptography, sensing, and metrology. For applications that require nanooptics, single-particle, and plasmonic excitations each play a key role. Single-particle excitations provide the discrete energies needed for frequency-selective emission, lasing and detection. Plasmons can be used to enhance and control the coupling of light to these emitters. However, in nanoscale and atomic-scale materials, the character of the optical excitations is often strongly mixed. This becomes especially troublesome when a quantum description of these excitations is needed, because there is no clear cut way to define their quantization. It is not even clear whether they should be treated as bosons or fermions. To move toward a quantum theory for these materials and their optical excitations, the optical excitations must first be characterized.

We have shown that TDDFT can be used to make that characterization provided that both the charge density induced by the excitation and the transitions that make up the excitation are analyzed. Single-particle-like excitations are primarily made from the single-electron transitions with transition energies close to the excitation energies. These transitions grow monotonically in time when the excitation is driven on resonance, depleting low-energy states well inside the Fermi sea and filling states high above the Fermi level. In contrast, for plasmonic excitations, charge sloshes back and forth from just below the Fermi level to just above the Fermi level. These differences in time dependence and in the states involved in the transitions that make up the excitation are key signatures that distinguish single-particle from plasmonic, collective excitations. The induced charge density from the sloshing charge is localized near the surface, as expected for surface plasmons, while the induced charge of the single-particle-like excitations reflects the charge distribution for the single-electron orbitals that are involved.

A different picture emerges for nanosystems, such as linear atomic chains, that are small enough for exact calculations of the excitation spectra to be done. The results for the exact calculations are in striking contrast to predictions of density functional theory. Density functional theory shows that single-particle-like and collective excitations can coexist. The exact calculations predict that the single-particle excitations evolve into collective excitations as the electron–electron interaction strength is turned on. There is no indication that both well-defined single-particle-like excitations and well-defined collective, plasmon-like excitations will coexist at the same interaction strength.

These qualitatively different predictions are a challenge for theory that must be resolved to understand quantum excitations in these systems. We have used TDDFT to study metal nanoparticles with one to six hundred electrons. In contrast, our exact calculations for the entire excitation spectra were restricted to systems with up to 8 electrons. Larger systems with more electrons can be studied using the same model. Although it becomes impractical to find an entire spectrum for a larger system, parts of the spectrum can be determined. In future work, we will study the low-energy spectra of larger systems to see if the differences between exact calculations and density functional theory depend on the number of electrons in this system. Understanding this dependence on electron number will provide an important insight on when and how plasmonic excitations appear in nanoplasmonic structures.