Article contents
Calculation of solid–liquid interfacial free energy of silicon based on classical nucleation theory
Published online by Cambridge University Press: 05 December 2016
Abstract
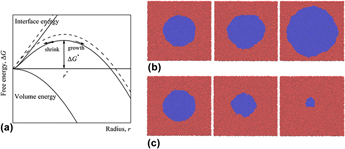
The solid–liquid interfacial free energy of silicon was calculated by the method based on classical nucleation theory (CNT), where the molecular dynamic (MD) simulations were carried out, and a series of cylindrical solid nuclei were equilibrated with undercooled liquid phase to create an ideal model of a homogeneous nucleation. The interfacial free energy was extracted from the relationship between the critical nuclei radii and their corresponding equilibrium temperatures. The influence of the interfacial curvature on its free energy was for the first time considered in our work, the influence can be measured by a Tolman length which was introduced to modify the traditional CNT; therefore, more accurate results were obtained. The averaged melting point and Tolman length extracted from simulations were 1678.27 K and 2.82 Å, respectively, which are consistent with the expected results. The averaged interfacial free energy is 401.92 mJ/m2, which is in good agreement with the results from experiments.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2016
References
REFERENCES
- 10
- Cited by


