Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T13:09:52.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Comment to “Skeletonization-based beam finite element models for stochastic bicontinuous materials: Application to simulations of nanoporous gold” by C. Soyarslan et al. [J. Mater. Res. 33(20), 3371 (2018)]

Published online by Cambridge University Press:  07 October 2020

Norbert Huber Open the ORCID record for Norbert Huber [Opens in a new window]  and
Claudia Richert
Norbert Huber*
Affiliation:
Institute of Materials Research, Materials Mechanics, Helmholtz-Zentrum Geesthacht, Max-Planck-Str. 1, 21502Geesthacht, Germany Institute of Materials Physics and Technology, Hamburg University of Technology, Eissendorfer Str. 42, 21073Hamburg, Germany
Claudia Richert
Affiliation:
Institute of Materials Research, Materials Mechanics, Helmholtz-Zentrum Geesthacht, Max-Planck-Str. 1, 21502Geesthacht, Germany
*
a)Address all correspondence to this author. e-mail: norbert.huber@hzg.de
Get access

Abstract

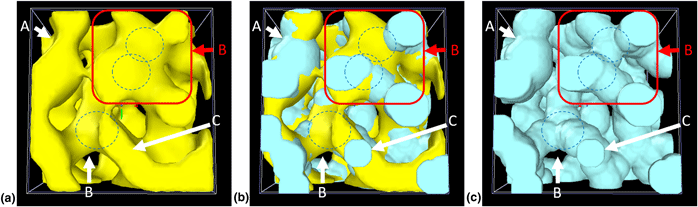
Soyarslan et al. [J. Mater. Res. 33(20), 3371 (2018)] proposed a beam-finite element model for the computation of effective elastic properties of nanoporous materials, where the ligament diameter along the skeleton is determined with the biggest sphere algorithm. Although this algorithm is often used in the literature, it is known that it systematically overestimates the diameter in network structures. Thus, the need for further stiffening of the junction zones as proposed by the authors is in contradiction to the literature. Furthermore, the factor 40 appears to be one order of magnitude too high. We show that the 3D microstructures generated from random Gaussian fields contain features that are violating the assumption of circular cross-sections and, therefore, cannot be captured by the biggest sphere algorithm. Consequently, the authors required an unphysically high value of 40 to compensate this hidden effect.

Keywords

microstructuremodelingelastic properties
Type
Commentary
Information
Journal of Materials Research , Volume 35 , Issue 20 , 28 October 2020 , pp. 2831 - 2834
Check for updates
Copyright
Copyright © The Author(s), 2020, published on behalf of Materials Research Society by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Huber, N., Viswanath, R., Mameka, N., Markmann, J., and Weißmüller, J.: Scaling laws of nanoporous metals under uniaxial compression. Acta Mater. 67, 252–265 (2014).CrossRefGoogle Scholar
Jiao, J. and Huber, N.: Effect of nodal mass on macroscopic mechanical properties of nanoporous metals. Int. J. Mech. Sci. 134, 234–243 (2017).CrossRefGoogle Scholar
Ngô, B.-N., Stukowski, A., Mameka, N., Markmann, J., Albe, K., and Weissmüller, J.: Anomalous compliance and early yielding of nanoporous gold. Acta Mater. 93, 144–155 (2015).CrossRefGoogle Scholar
Mangipudi, K., Epler, E., and Volkert, C.: Topology-dependent scaling laws for the stiffness and strength of nanoporous gold. Acta Mater. 119, 115–122 (2016).CrossRefGoogle Scholar
Hu, K., Ziehmer, M., Wang, K., and Lilleodden, E.: Nanoporous gold: 3D structural analyses of representative volumes and their implications on scaling relations of mechanical behaviour. Philos. Magaz. 96, 3322–3335 (2016).CrossRefGoogle Scholar
Hu, K.: Micromechanical and three-dimensional microstructural characterization of nanoporous gold–epoxy composites. Ph.D. thesis, Hamburg University of Technology (TUHH), 2017Google Scholar
Richert, C. and Huber, N.: Skeletonization, geometrical analysis and finite element modeling of nanoporous gold based on 3D tomography data. Metals 8, 282 (2018).CrossRefGoogle Scholar
Soyarslan, S., Bargmann, S., Pradas, M., and Weissmüller, J.: 3D stochastic bicontinuous microstructures: Generation, topology and elasticity. Acta Mater. 149, 326–340 (2018).CrossRefGoogle Scholar
Hildebrand, T. and Rüegsegger, P.: A new method for the model-independent assessment of thickness in three-dimensional images. J. Microsc. 185, 67–75 (1997).CrossRefGoogle Scholar
Richert, C., Odermatt, A., and Huber, N.: Computation of thickness and mechanical properties of interconnected structures: Accuracy, deviations and approaches for correction. Front. Mater. 6, 352 (2019).CrossRefGoogle Scholar
Odermatt, A., Richert, C., and Huber, N.: Prediction of elastic-plastic deformation of nanoporous metals by FEM beam modeling: A bottom-up approach from ligaments to real microstructures. Mater. Sci. Eng. A 791, 139700 (2020).CrossRefGoogle Scholar
Soyarslan, C., Argeso, H., and Bargmann, S.: Skeletonization-based beam finite element models for stochastic bicontinuous materials: Application to simulations of nanoporous gold. J. Mater. Res. 33, 3371–3382 (2018).CrossRefGoogle Scholar
Bargmann, S., Klusemann, B., Markmann, J., Schnabel, J., Schneider, K.S.C., and Wilmers, J.: Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 96, 322–384 (2018).CrossRefGoogle Scholar
Stukowski, A.: Visualization and analysis of atomistic simulation data with OVITO – the Open Visualization Tool. Modelling Simul. Mater. Sci. Eng. 18, 015012 (2010).CrossRefGoogle Scholar