Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T15:08:11.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Contact-area-based FEA study on conical indentation problems for elastoplastic and viscoelastic-plastic bodies

Published online by Cambridge University Press:  17 November 2011

Mototsugu Sakai ,
Shun Kawaguchi  and
Norio Hakiri
Mototsugu Sakai*
Affiliation:
Department of Materials Science, Toyohashi University of Technology, Toyohashi 441-8580, Japan
Shun Kawaguchi
Affiliation:
Department of Materials Science, Toyohashi University of Technology, Toyohashi 441-8580, Japan
Norio Hakiri
Affiliation:
Department of Materials Science, Toyohashi University of Technology, Toyohashi 441-8580, Japan
*
a)Address all correspondence to this author. e-mail: msakai@tutms.tut.ac.jp
Get access

Abstract

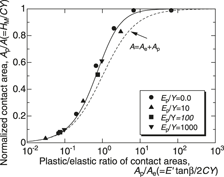
The authors discuss the contact-area-based indentation contact mechanics instead of the conventional penetration-depth-based analysis. In time-independent elastoplastic regime, the indentation load P versus contact area A relationship for a cone indentation is linear both for the loading and the unloading paths. The slope of the loading path directly yields the Meyer hardness HM, and the slope of the unloading path, i.e., the unloading modulus M, is related to the elastic modulus E′ through the relation of M = E′tan β/2. The relation of the total contact area A to the purely elastic and the purely plastic contact areas of Ae and Ap are theoretically as well as numerically examined. The normalized relationship between Ap/A versus Ap/Ae is equivalent to the Johnson’s hardness plot of HM/Y versus E′tan β/Y. By extending the concept of Ae and Ap to time-dependent viscoelastic-plastic regime, a detailed discussion is made how to eliminate the plastic deformation/flow from the total contact area A(t) to yield the viscoelastic contact area Ave(t) prior to determining the linear-viscoelastic parameters and functions.

Keywords

Elastic propertiesHardnessNanoindentation
Type
Articles
Information
Journal of Materials Research , Volume 27 , Issue 1: Focus Issue: Instrumented Indentation , 14 January 2012 , pp. 256 - 265
Copyright
Copyright © Materials Research Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Johnson, K.L.: Contact Mechanics (Cambridge University Press, Cambridge, 1985), Chap. 6.CrossRefGoogle Scholar
2.Tabor, D.: Hardness of Materials (Clarendon Press, Oxford, 1951).Google Scholar
3.Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564 (1992).CrossRefGoogle Scholar
4.Miyajima, T. and Sakai, M.: Optical indentation microscopy—a new family of instrumented indentation testing. Philos. Mag. 86, 5729 (2006).CrossRefGoogle Scholar
5.Sakai, M. and Hakiri, N.: Instrumented indentation microscope: A powerful tool for the mechanical characterization in micro-scales. J. Mater. Res. 21, 2298 (2006).CrossRefGoogle Scholar
6.Hakiri, N., Matsuda, A., and Sakai, M.: Instrumented indentation microscope applied to the elastoplastic indentation contact mechanics of coating/substrate composites. J. Mater. Res. 24, 1950 (2009).CrossRefGoogle Scholar
7.Sneddon, I.N.: The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 3, 47 (1965).Google Scholar
8.Sakai, M., Akatsu, T., Numata, S., and Matsuda, K.: Linear strain hardening in elastoplastic indentation contact. J. Mater. Res. 18, 2087 (2003).CrossRefGoogle Scholar
9.Shames, I.H. and Cozzarelli, F.A.: Elastic and Inelastic Stress Analysis (Prentice Hall, Englewood Cliff, 1992), Chap. 6.Google Scholar
10.Roylance, D.: Mechanics of Materials (Wiley, New York, 1996), Chaps. 2 and 3.Google Scholar
11.Radok, J.R.M.: Visco-elastic stress analysis. Q. Appl. Math. 15, 198 (1957).Google Scholar
12.Sakai, M. and Shimizu, S.: Indentation rheometry for glass-forming materials. J. Non-Cryst. Solids 282, 236 (2001).CrossRefGoogle Scholar
13.Sakai, M. and Shimizu, S.: Viscoelastic indentation of silicate glasses. J. Am. Ceram. Soc. 85, 1210 (2002).CrossRefGoogle Scholar
14.Sakai, M.: FEA-study on the viscoelastic Poisson’s ratio in indentation contact problems. Mech. Time-Depend. Mater. (submitted to).Google Scholar
15.Vanlandingham, M.R., Chang, N-K., Drzal, P.L., White, C.C., and Chang, S-H.: Viscoelastic characterization of polymers using instrumented indentation. I. Quasi-static testing. J. Polym. Sci. Part B: Polym. Phys. 43, 1794 (2005).CrossRefGoogle Scholar
16.ANSYS Academic Research Release V. 10.0, ANSYS Inc. Canonsburg, PA.Google Scholar
17.Hay, J.C., Bolshakov, A., and Pharr, G.M.: A critical examination of the fundamental relations used in the analysis of nanoindentation data. J. Mater. Res. 14, 2296 (1999).Google Scholar