Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T04:51:35.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Crystal plasticity modeling the deformation in nanodomained heterogenous structures

Published online by Cambridge University Press:  06 March 2019

Tianju Chen Open the ORCID record for Tianju Chen [Opens in a new window]  and
Caizhi Zhou
Tianju Chen
Affiliation:
Department of Materials Science and Engineering, Missouri University of Science and Technology, Rolla, Missouri 65409, USA
Caizhi Zhou*
Affiliation:
Department of Materials Science and Engineering, Missouri University of Science and Technology, Rolla, Missouri 65409, USA
*
a)Address all correspondence to this author. e-mail: zhouc@mst.edu
Get access

Abstract

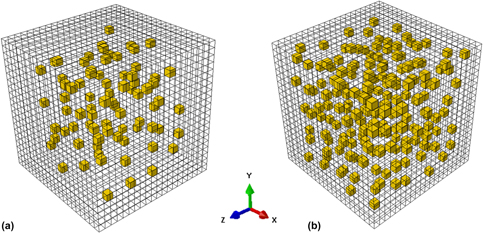
Nanodomained heterogenous structures characterized by randomly dispersed nanograins (NGs) embedded in the coarser grains (CGs) have demonstrated an exciting potential to break the strength–ductility trade-off, providing high strength without the loss of ductility. Here, using a combination of discrete crystal plasticity finite element (discrete-CPFE) model and dislocation density-based CPFE model, we study the effects of grain size, volume fraction of nanograins on the strength and deformation in nanodomained materials. Our analysis shows that the overall flow stresses of nanodomained samples are equal or higher than the strengths predicted by rule of mixtures. Smaller NGs or higher volume fraction of NGs can make the nanodomained samples stronger, as they can be more effective to promote the dislocation accumulations inside the CGs and eventually raise the critical resolved shear stress for each slip system during the plastic flow. Areas surrounding NGs stored higher dislocation densities and less plastic strain, due to the restricted dislocation motion. Furthermore, NGs grain embedded in the CGs can effectively reduce the anisotropy of strength in the nanodomained samples.

Keywords

nanodomaingrain sizecrystal plasticitynanocrystallinefinite element model
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 9: Focus Issue: Plasticity and Fracture at the Nanoscales - Advances in in situ Experimentation Techniques Enabling Novel and Extreme Materials/Nanocomposite Design , 14 May 2019 , pp. 1555 - 1563
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Lu, K.: Making strong nanomaterials ductile with gradients: Microstructures that increase metal crystallite size from nanoscale with surface depth are both strong and ductile. Science 345, 1455 (2014).CrossRefGoogle Scholar
Fang, T.H., Li, W.L., Tao, N.R., and Lu, K.: Revealing extraordinary intrinsic tensile plasticity in gradient nano-grained copper. Science 331, 1587 (2011).CrossRefGoogle ScholarPubMed
Wu, X., Jiang, P., Chen, L., Yuan, F., and Zhu, Y.T.: Extraordinary strain hardening by gradient structure. Proc. Natl. Acad. Sci. U. S. A. 111, 7197 (2014).CrossRefGoogle ScholarPubMed
Wu, X.L., Jiang, P., Chen, L., Zhang, J.F., Yuan, F.P., and Zhu, Y.T.: Synergetic strengthening by gradient structure. Mater. Res. Lett. 2, 185 (2014).CrossRefGoogle Scholar
Chen, A., Liu, J., Wang, H., Lu, J., and Wang, Y.M.: Gradient twinned 304 stainless steels for high strength and high ductility. Mater. Sci. Eng., A 667, 179 (2016).CrossRefGoogle Scholar
Wei, Y., Li, Y., Zhu, L., Liu, Y., Lei, X., Wang, G., Wu, Y., Mi, Z., Liu, J., Wang, H., and Gao, H.: Evading the strength–ductility trade-off dilemma in steel through gradient hierarchical nanotwins. Nat. Commun. 5, 3580 (2014).CrossRefGoogle ScholarPubMed
Wu, X., Yang, M., Yuan, F., Wu, G., Wei, Y., Huang, X., and Zhu, Y.: Heterogeneous lamella structure unites ultrafine-grain strength with coarse-grain ductility. Proc. Natl. Acad. Sci. U. S. A. 112, 14501 (2015).CrossRefGoogle ScholarPubMed
Han, B.Q., Lee, Z., Witkin, D., Nutt, S., and Lavernia, E.J.: Deformation behavior of bimodal nanostructured 5083 Al alloys. Metall. Mater. Trans. A 36, 957 (2005).CrossRefGoogle Scholar
Sawangrat, C., Kato, S., Orlov, D., and Ameyama, K.: Harmonic-structured copper: Performance and proof of fabrication concept based on severe plastic deformation of powders. J. Mater. Sci. 49, 6579 (2014).CrossRefGoogle Scholar
Ma, X., Huang, C., Moering, J., Ruppert, M., Höppel, H.W., Göken, M., Narayan, J., and Zhu, Y.: Mechanical properties of copper/bronze laminates: Role of interfaces. Acta Mater. 116, 43 (2016).CrossRefGoogle Scholar
Zhao, Y., Topping, T., Bingert, J.F., Thornton, J.J., Dangelewicz, A.M., Li, Y., Liu, W., Zhu, Y., Zhou, Y., and Lavernia, E.J.: High tensile ductility and strength in bulk nanostructured nickel. Adv. Mater. 20, 3028 (2008).CrossRefGoogle Scholar
Wang, Y., Chen, M., Zhou, F., and Ma, E.: High tensile ductility in a nanostructured metal. Nature 419, 912 (2002).CrossRefGoogle Scholar
Han, B.Q., Huang, J.Y., Zhu, Y.T., and Lavernia, E.J.: Strain rate dependence of properties of cryomilled bimodal 5083 Al alloys. Acta Mater. 54, 3015 (2006).CrossRefGoogle Scholar
Wu, X., Yuan, F., Yang, M., Jiang, P., Zhang, C., Chen, L., Wei, Y., and Ma, E.: Nanodomained nickel unite nanocrystal strength with coarse-grain ductility. Sci. Rep. 5, 11728 (2015).CrossRefGoogle ScholarPubMed
Huang, S., Wang, J., Li, N., Zhang, J., and Zhou, C.: Atomistic simulations of plasticity in heterogeneous nanocrystalline Ni lamella. Comput. Mater. Sci. 141, 229 (2018).CrossRefGoogle Scholar
Huang, S., Wang, J., and Zhou, C.: Deformation of heterogeneous nanocrystalline lamella with a preexisting crack. JOM 70, 60 (2018).CrossRefGoogle Scholar
Roters, F., Eisenlohr, P., Hantcherli, L., Tjahjanto, D.D., Bieler, T.R., and Raabe, D.: Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 58, 1152 (2010).CrossRefGoogle Scholar
Meyers, M.A. and Chawla, K.K.: Mechanical Behavior of Materials (Cambridge University Press, Cambridge, U.K., 2009).Google Scholar
Rupert, T., Gianola, D., Gan, Y., and Hemker, K.: Experimental observations of stress-driven grain boundary migration. Science 326, 1686 (2009).CrossRefGoogle ScholarPubMed
Huang, S., Beyerlein, I.J., and Zhou, C.: Nanograin size effects on the strength of biphase nanolayered composites. Sci. Rep. 7, 11251 (2017).CrossRefGoogle ScholarPubMed
Brandl, C., Tiwari, S., Derlet, P.M., and Van Swygenhoven, H.: Athermal critical stresses for dislocation propagation in nanocrystalline aluminium. Philos. Mag. 90, 977 (2010).CrossRefGoogle Scholar
Huang, S. and Zhou, C.: Modeling and simulation of nanoindentation. JOM 69, 2256 (2017).CrossRefGoogle Scholar
Zhou, C., Beyerlein, I.J., and LeSar, R.: Plastic deformation mechanisms of fcc single crystals at small scales. Acta Mater. 59, 7673 (2011).CrossRefGoogle Scholar
Zhou, C., Biner, S.B., and LeSar, R.: Discrete dislocation dynamics simulations of plasticity at small scales. Acta Mater. 58, 1565 (2010).CrossRefGoogle Scholar
Marin, E.B. and Dawson, P.R.: On modelling the elasto-viscoplastic response of metals using polycrystal plasticity. Comput. Methods Appl. Mech. Eng. 165, 1 (1998).CrossRefGoogle Scholar
Yuan, R., Beyerlein, I.J., and Zhou, C.: Emergence of grain-size effects in nanocrystalline metals from statistical activation of discrete dislocation sources. Acta Mater. 90, 169 (2015).CrossRefGoogle Scholar
Yuan, R., Beyerlein, I.J., and Zhou, C.: Coupled crystal orientation-size effects on the strength of nano crystals. Sci. Rep. 6, 26254 (2016). (Accepted).CrossRefGoogle ScholarPubMed
Foreman, A.: The bowing of a dislocation segment. Philos. Mag. 15, 1011 (1967).CrossRefGoogle Scholar
Madec, R., Devincre, B., and Kubin, L.: From dislocation junctions to forest hardening. Phys. Rev. Lett. 89, 255508 (2002).CrossRefGoogle ScholarPubMed
Li, J. and Soh, A.: Modeling of the plastic deformation of nanostructured materials with grain size gradient. Int. J. Plast. 39, 88 (2012).CrossRefGoogle Scholar
Mecking, H. and Kocks, U.: Kinetics of flow and strain-hardening. Acta Metall. 29, 1865 (1981).CrossRefGoogle Scholar
Ma, A., Roters, F., and Raabe, D.: A dislocation density based constitutive model for crystal plasticity FEM including geometrically necessary dislocations. Acta Mater. 54, 2169 (2006).CrossRefGoogle Scholar
Jahedi, M., Ardeljan, M., Beyerlein, I.J., Paydar, M.H., and Knezevic, M.: Enhancement of orientation gradients during simple shear deformation by application of simple compression. J. Appl. Phys. 117, 214309 (2015).CrossRefGoogle Scholar
Li, L., Anderson, P.M., Lee, M-G., Bitzek, E., Derlet, P., and Van Swygenhoven, H.: The stress–strain response of nanocrystalline metals: A quantized crystal plasticity approach. Acta Mater. 57, 812 (2009).CrossRefGoogle Scholar
Zhu, R., Zhou, J., Jiang, H., and Zhang, D.: Evolution of shear banding in fully dense nanocrystalline Ni sheet. Mech. Mater. 51, 29 (2012).CrossRefGoogle Scholar
Ebrahimi, F., Bourne, G., Kelly, M.S., and Matthews, T.: Mechanical properties of nanocrystalline nickel produced by electrodeposition. Nanostruct. Mater. 11, 343 (1999).CrossRefGoogle Scholar
Ma, E. and Zhu, T.: Towards strength–ductility synergy through the design of heterogeneous nanostructures in metals. Mater. Today 20, 323 (2017).CrossRefGoogle Scholar
Choi, S-H., Kim, E-Y., Woo, W., Han, S., and Kwak, J.: The effect of crystallographic orientation on the micromechanical deformation and failure behaviors of DP980 steel during uniaxial tension. Int. J. Plast. 45, 85 (2013).CrossRefGoogle Scholar