Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T11:14:31.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential scanning calorimetric measurements and thermodynamic functions of YbRhO3(s)

Published online by Cambridge University Press:  31 October 2018

Aparna Banerjee Open the ORCID record for Aparna Banerjee [Opens in a new window]
Aparna Banerjee*
Affiliation:
Fuel Chemistry Division, RC & I Group, Bhabha Atomic Research Centre, Mumbai 400 085, India
*
a)Address all correspondence to this author. e-mail: aparnab@barc.gov.in, aparna_baner@yahoo.com
Get access

Abstract

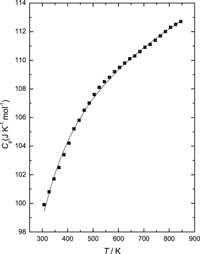
Standard molar heat capacity, $C_{{\rm{p,m}}}^{\rm{o}}\left( T \right)$, of YbRhO3(s) was determined using a heat flux type differential scanning calorimeter from 126 to 846 K. The heat capacities in the temperature range 307 ≤ T (K) ≤ 846 were fitted into a polynomial expression and can be represented by $C_{{\rm{p,m}}}^{\rm{o}}$ (YbRhO3, s, T) [J/(K mol)] = 106.82 + 8.57 × 10−3T (K) − 9.48 × 105/T2(K). The standard molar heat capacity of YbRhO3(s), $C_{{\rm{p,m}}}^{\rm{o}}$, at 298.15 K is 98.7 J/(K mol). The standard molar Gibbs energy of formation of YbRhO3(s) was also determined using calcia stabilized zirconia as an oxide electrolyte and air as the reference electrode by the solid state electrochemical technique. The cell can be represented by (−)Pt–Rh/{Yb2O3(s) + YbRhO3(s) + Rh(s)}//CSZ//O2(p(O2) = 21.21 kPa)/Pt–Rh(+). The electromotive force was measured in the temperature range from 889 to 1110 K. The standard Gibbs energy of formation of YbRhO3(s) from elements in their standard state can be represented by ΔfGo{YbRhO3(s)}/kJ/mol(±1.62) = −1110.9 + 0.287 T (K). The heat capacity of YbRhO3(s) was used along with the data obtained from the electrochemical cell to evaluate all thermodynamic functions of YbRhO3(s).

Keywords

Ybcalorimetryionic conductorperovskites
Type
Article
Information
Journal of Materials Research , Volume 33 , Issue 23 , 14 December 2018 , pp. 3979 - 3985
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Scott, J.F.: Nanoferroelectrics: Statics and dynamics. J. Phys.: Condens. Matter 18, 361 (2006).Google ScholarPubMed
Bokov, A.A. and Ye, Z-G.: Recent progress in relaxor ferroelectrics with perovskite structure. J. Mater. Sci. 41, 31 (2006).CrossRefGoogle Scholar
Ormerod, R.M.: Solid oxide fuel cells. Chem. Soc. Rev. 32, 17 (2003).CrossRefGoogle ScholarPubMed
Keav, S., Matam, S., Ferri, D., and Weidenkaff, A.: Structured perovskite-based catalysts and their application as three-way catalytic converters—A review. Catalysis 4, 226 (2014).Google Scholar
Jarret, H.S., Sleight, A.W., Kung, H.H., and Gilson, J.L.: Photoelectrochemical properties of LuRhO3(s). Surf. Sci. 101, 205 (1980).CrossRefGoogle Scholar
Nakamura, T., Shimura, T., Ito, M., and Ikeda, Y.: Magnetic and electric properties of La1−xMxRhO3 (M = Ca, Sr, and Ba): Hole doping in 4dε orbitals of Rh3+ with low spin configuration. J. Solid State Chem. 103, 523 (1993).CrossRefGoogle Scholar
Carriero, L., Qian, Y.T., Kershaw, R., Dwight, K., and Wold, A.: Stability of several iron and rhodium ternary oxides in a reducing atmosphere. Mater. Res. Bull. 20, 619 (1985).CrossRefGoogle Scholar
Taniguchi, T., Iizuka, W., Nagata, Y., Uchida, T., and Samata, H.: Magnetic properties of RRhO3 (R = rare earth). J. Alloys Compd. 350, 24 (2003).CrossRefGoogle Scholar
Tahidul Haque, M., Satoh, H., and Kamegashira, N.: Crystallographic phase transition, electrical and magnetic properties of stoichiometric La(Mn,Rh)O3. J. Alloys Compd. 390, 115 (2005).Google Scholar
Mary, T.A. and Varadaraju, U.V.: Orthorhombic-tetragonal and semiconductor-metal transitions in the La1−xSrxRhO3 system. J. Solid State Chem. 110, 176 (1994).CrossRefGoogle Scholar
Watson, P.R. and Somorjai, G.A.: Synthesis gas conversion with perovskite catalysts. J. Catal. 74, 282 (1982).CrossRefGoogle Scholar
Jarrett, H.S., Sleight, A.W., Kung, H.H., and Gillson, J.L.: Photoelectrochemical and solid-state properties of LuRhO3. J. Appl. Phys. 51, 3916 (1980).CrossRefGoogle Scholar
Ohnishi, T., Taniguchi, T., Ikoshi, A., Mizusaki, S., Nagata, Y., Lai, S.H., Lan, M.D., Noro, Y., Ozawa, T.C., Kindo, K., Matsuo, A., and Takayanagi, S.: Antiferromagnetism of LnRhO3. J. Alloys Compd. 506, 27 (2010).CrossRefGoogle Scholar
Shannon, R.D.: Cell dimensions of rare earth orthorhodites. Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 26, 447 (1970).CrossRefGoogle Scholar
Goldschmidt, V.M.: Die Gesetze der Krystallochemie. Naturwissenschaften 14, 477 (1926).CrossRefGoogle Scholar
Shannon, R.D.: Synthesis of some new perovskites containing indium and thallium. Inorg. Chem. 6, 1474 (1967).CrossRefGoogle Scholar
Li, C., Soh, K.C.K., and Wu, P.: Formability of ABO3 perovskites. J. Alloys Compd. 372, 40 (2004).CrossRefGoogle Scholar
Lazarev, V.B. and Shaplygin, I.S.: Synthesis and properties of ytterbium rhodium oxide. Russ. J. Inorg. Chem. 23, 1131 (1978).Google Scholar
Kleykamp, H.: The chemical state of fission products in oxide fuels at different stages of the nuclear fuel cycle. Nucl. Technol. 80, 412 (1988).CrossRefGoogle Scholar
Jacob, K.T., Gupta, P., Han, D., and Uda, T.: Thermodynamic properties of YbRhO3 and phase relations in the system Yb–Rh–O. J. Phase Equilib. Diffus. 37, 50 (2016).CrossRefGoogle Scholar
Jacob, K.T. and Waseda, Y.: Solid state cells with buffer electrodes for measurement of chemical potentials and Gibbs energies of formation: System Ca–Rh–O. J. Solid State Chem. 150, 213 (2000).CrossRefGoogle Scholar
Sabbah, R., Xu-wu, A.N., Chickos, J.S., Planas Leitao, M.L., and Roux, M.V.: Torres LA Reference materials for calorimetry and differential thermal analysis. Thermochim. Acta 331, 93 (1999).CrossRefGoogle Scholar
Banerjee, A., Singh, Z., and Venugopal, V.: Heat capacity and Gibbs energy of formation of the ternary oxide CdRh2O4(s). Solid State Ionics 180, 1337 (2009).CrossRefGoogle Scholar
Hohne, G.W.H., Hemminger, W.F., and Flammershein, H.J.: Differential Scanning Calorimetry, 2nd ed. (Springer, Berlin, 2003).CrossRefGoogle Scholar
Chase, M.W. Jr.: NIST-JANAF Thermochemical Tables, 4th ed. J. Phys. Chem. (monograph no. 91995).Google Scholar
Banerjee, A., Prasad, R., and Venugopal, V.: Simultaneous determination of Gibbs free energies of formation of Sr2RhO4(s) and Sr4RhO6(s) using solid-state electrochemical cells. J. Alloys Compd. 381, 58 (2004).CrossRefGoogle Scholar
Kubachewski, O., Alcock, C.B., and Spencer, P.J.: Materials Thermochemistry, 6th ed. (Oxford, Pergamon, 1993); p. 167.Google Scholar
FactSage: Version 5.3.1: Thermo-Chemical Database Software, Thermfact (GTT Technologies, Germany, 1976–2004).Google Scholar
Jacob, K.T., Uda, T., Okabe, T.H., and Waseda, Y.: The standard enthalpy and entropy of formation of Rh2O3—A third law optimization. High Temp. Mater. Processes 19, 11 (2000).CrossRefGoogle Scholar
Nell, J., St, H., and O’Neill, C.: The Gibbs free energy of formation and heat capacity of β Rh2O3 and MgRh2O4, the MgO–RhO phase diagram and constraints on the stability of Mg2RhO4. Geochim. Cosmochim. Acta 61, 4159 (1997).CrossRefGoogle Scholar
Berg, J.R., Spedding, F.H., and Daane, A.H.: The high temperature heat contents and related thermodynamic properties of lanthanum, praseodymium, europium, ytterbium, and yttrium. Ph. D. thesis, Iowa State University of Science and Technology, July, 1961, by J. R. Berg. (submitted to).Google Scholar
Graves, K., Kirby, B., and Rardin, R.: FREED Version 2.1 (1991).Google Scholar