Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T14:58:32.626Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective Poisson’s ratio from combined normal and lateral contacts of single crystals

Published online by Cambridge University Press:  26 October 2011

J.H. Lee ,
Y.F. Gao  and
G.M. Pharr
J.H. Lee*
Affiliation:
Division for Research Reactor, Korea Atomic Energy Research Institute, Daejeon 305-353, Republic of Korea
Y.F. Gao*
Affiliation:
Department of Materials Science and Engineering, University of Tennessee, Knoxville, Tennessee 37996; and Computer Science and Mathematics Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831
G.M. Pharr
Affiliation:
Department of Materials Science and Engineering, University of Tennessee, Knoxville, Tennessee 37996; and Materials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831
*
a)Address all correspondence to these authors. e-mail: jinhaeng@kaeri.re.kr
b)e-mail: ygao7@utk.edu
Get access

Abstract

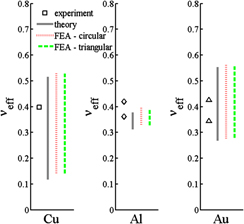
When an elastic half-space is subjected to both normal and tangential contact, the ratio of normal and tangential contact stiffnesses can be measured by various scanning force microscopy techniques. For elastically isotropic solids, this stiffness ratio depends on Poisson’s ratio as given by the Mindlin solution. An anisotropic elastic contact analysis here shows the difference between the effective Poisson’s ratio as defined from the stiffness ratio and its uniaxial counterpart with respect to various crystal structures and various normal/tangential contact directions. Closed-form analytical solutions of effective indentation moduli are derived for materials with at least one plane of transverse isotropy. Since the Sneddon (normal contact) and Mindlin (lateral contact) solutions are derived under different frictional conditions, finite element simulations were performed which show that the effects of elastic dissimilarity and contact shape are generally small but not negligible. The predicted dependence on crystallographic orientation and elastic anisotropy has been compared favorably with previously reported multiaxial contact experiments for a number of cubic single crystals. Implications for atomic force microscopy based experiments are also discussed.

Keywords

NanoindentationElastic properties
Type
Articles
Information
Journal of Materials Research , Volume 27 , Issue 1: Focus Issue: Instrumented Indentation , 14 January 2012 , pp. 182 - 191
Copyright
Copyright © Materials Research Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Carpick, R.W., Ogletree, D.F., and Salmeron, M.: Lateral stiffness: a new nanomechanical measurement for the determination of shear strengths with friction force microscopy. Appl. Phys. Lett. 70, 1548 (1997).CrossRefGoogle Scholar
2.Hurley, D.C. and Turner, J.A.: Measurement of Poisson’s ratio with contact-resonance atomic force microscopy. J. Appl. Phys. 102, 033509 (2007).CrossRefGoogle Scholar
3.Stan, G. and Cook, R.F.: Mapping the elastic properties of granular Au films by contact resonance atomic force microscopy. Nanotechnology 19, 235701 (2008).CrossRefGoogle ScholarPubMed
4.Reinstädtler, M., Kasai, T., Rabe, U., Bhushan, B., and Arnold, W.: Imaging and measurement of elasticity and friction using the TR mode. J. Phys. D: Appl. Phys. 38, R269 (2005).CrossRefGoogle Scholar
5.Lucas, B.N., Hay, J.C., and Oliver, W.C.: Using multidimensional contact mechanics experiments to measure Poisson’s ratio. J. Mater. Res. 19, 58 (2004).CrossRefGoogle Scholar
6.Gao, Y.F., Lucas, B.N., Hay, J.C., Oliver, W.C., and Pharr, G.M.: Nanoscale incipient asperity sliding and interface micro-slip assessed by the measurement of tangential contact stiffness. Scr. Mater. 55, 653 (2006).CrossRefGoogle Scholar
7.Gao, Y.F., Xu, H.T., Oliver, W.C., and Pharr, G.M.: A comparison of Coulomb friction and friction stress models based on multidimensional nanocontact experiments. J. Appl. Mech. 75, 034504 (2008).CrossRefGoogle Scholar
8.Johnson, K.L.: Contact Mechanics (Cambridge University Press, Cambridge, 1985).CrossRefGoogle Scholar
9.Gao, Y.F. and Pharr, G.M.: Multidimensional contact moduli of elastically anisotropic solids. Scr. Mater. 57, 13 (2007).CrossRefGoogle Scholar
10.Baughman, R.H., Shacklette, J.M., Zakhidov, A.A., and Stafstroem, S.: Negative Poisson’s ratios as a common feature of cubic metals. Nature 392, 362 (1998).CrossRefGoogle Scholar
11.Ting, T.C.T. and Barnett, D.M.: Negative Poisson’s ratios in anisotropic linear elastic media. J. Appl. Mech. 72, 929 (2005).CrossRefGoogle Scholar
12.Ting, T.C.T. and Chen, T.Y.: Poisson’s ratio for anisotropic elastic materials can have no bounds. Q. J. Mech. Appl. Math. 58, 73 (2005).CrossRefGoogle Scholar
13.Lethbridge, Z.A.D., Walton, R.I., Marmier, A.S.H., Smith, C.W., and Evans, K.E.: Elastic anisotropy and extreme Poisson’s ratios in single crystals. Acta Mater. 58, 6444 (2010).CrossRefGoogle Scholar
14.Vlassak, J.J. and Nix, W.D.: Indentation modulus of elastically anisotropic half spaces. Philos. Mag. A 67, 1045 (1993).CrossRefGoogle Scholar
15.Vlassak, J.J. and Nix, W.D.: Measuring the elastic properties of anisotropic materials by means of indentation experiments. J. Mech. Phys. Solids 42, 1223 (1994).CrossRefGoogle Scholar
16.Bower, A.F.: Applied Mechanics of Solids (CRC Press, Boca Raton, FL, 2009).CrossRefGoogle Scholar
17.Espinasse, L., Keer, L., Borodich, F., Yu, H., and Wang, Q.J.: A note on JKR and DMT theories of contact on a transversely isotropic half-space. Mech. Mater. 42, 477 (2010).CrossRefGoogle Scholar
18.Gao, Y.F., Xu, H.T., Oliver, W.C., and Pharr, G.M.: Effective elastic modulus of film-on-substrate systems under normal and tangential contact. J. Mech. Phys. Solids 56, 402 (2008).CrossRefGoogle Scholar
19.Lee, H., Lee, J.H., and Pharr, G.M.: A numerical approach to spherical indentation techniques for material property evaluation. J. Mech. Phys. Solids 53, 2037 (2005).CrossRefGoogle Scholar
20.Lee, J.H., Lee, H., and Kim, D.H.: A numerical approach to evaluation of elastic modulus using conical indenter with finite tip radius. J. Mater. Res. 23, 2528 (2008).CrossRefGoogle Scholar
21.Lee, J.H., Kim, T.H., and Lee, H.: A study on robust indentation techniques to evaluate elastic-plastic properties of metals. Int. J. Solids Struct. 47, 647 (2010).CrossRefGoogle Scholar
22.Annett, J., Gao, Y.F., Cross, G.L.W., Herbert, E.G., and Lucas, B.N.: Mesoscale friction anisotropy revealed by slidingless tests. J. Mater. Res. 26(18), 2373 (2011).CrossRefGoogle Scholar