Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T05:57:59.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Evaluation of tensile yield strength of high-density polyethylene in flat-ended cylindrical indentation: An analytic approach based on the expanding cavity model

Published online by Cambridge University Press:  10 January 2020

Jongho Won ,
Seunggyu Kim ,
Oh Min Kwon ,
Young-Cheon Kim  and
Dongil Kwon
Jongho Won
Affiliation:
Department of Materials Science and Engineering, Seoul National University, Seoul 08826, Korea; and Centre for Advanced Innovation Technologies (CPIT), VSB-Technical University of Ostrava, Ostrava 70800, Czech Republic
Seunggyu Kim
Affiliation:
Facility Team, Samsung Electronics, Hwaseong 18448, Korea
Oh Min Kwon
Affiliation:
Department of Materials Science and Engineering, Seoul National University, Seoul 08826, Korea
Young-Cheon Kim*
Affiliation:
Research Center for Energy and Clean Technology, School of Materials Science and Engineering, Andong National University, Andong, Gyeongbuk 36729, Korea
Dongil Kwon
Affiliation:
Department of Materials Science and Engineering, Seoul National University, Seoul 08826, Korea
*
a)Address all correspondence to this author. e-mail: kimyc@anu.ac.kr
Get access

Abstract

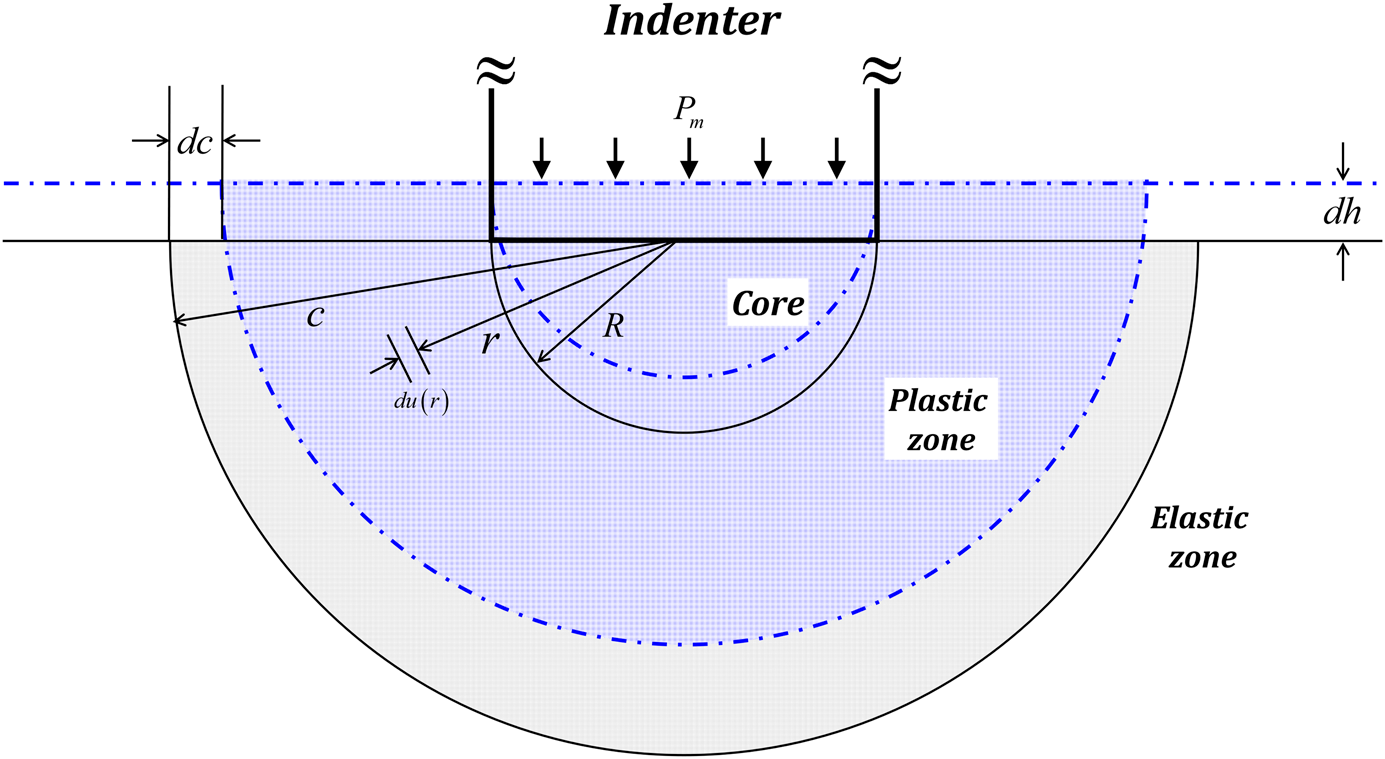
The tensile yield strength of high-density polyethylene using instrumented indentation tests with a flat-ended cylindrical indenter was evaluated. The variation in the field expressed by stress and strain beneath the flat-ended cylindrical indenter is investigated using a new expanding cavity model to study the relation between tension and indentation. This model starts from the separation of forces into the compressive force on the material and the frictional one, which is generated during indentation on the sides of indenter. The authors propose a method to correct the frictional force based on the saturation of indentation hardening and obtain load–depth curve with compressive component only. For conversion of indentation force and displacement, our new representation model is applied. By modifying Johnson's model, the new assumption of conservation of indentation plastic volume is suggested. This model proves and supports conventional relations of the strain rates between indentation and tension theoretically. These are verified through the experiments: instrumented indentation and uniaxial tensile test. The authors find a good agreement between the tensile yield strengths at various strain rates.

Keywords

polymerhardnessstrength
Type
Article
Information
Journal of Materials Research , Volume 35 , Issue 2 , 28 January 2020 , pp. 206 - 214
Check for updates
Copyright
Copyright © Materials Research Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

b)

These authors contributed equally to this work.

References

Peggs, I. and Kanninen, M.: HDPE geosynthetics: Premature failures and their prediction. Geosyn. Int. 2, 327 (1995).CrossRefGoogle Scholar
Shillitoe, S., Day, A., and Benkreira, H.: A finite element approach to butt fusion welding analysis. P. I. Mech. Eng. E-J. Pro. 204, 95 (1990).CrossRefGoogle Scholar
Lu, Y. and Shinozaki, D.: Deep penetration micro-indentation testing of high density polyethylene. Mater. Sci. Eng. A. 249, 134 (1998).CrossRefGoogle Scholar
Zhang, M-G., Chen, J., Feng, X-Q., and Cao, Y.: On the applicability of Sneddon's solution for interpreting the indentation of nonlinear elastic biopolymers. J. Appl. Mech. 81, 091011 (2014).10.1115/1.4027973CrossRefGoogle Scholar
American Society for Testing and Materials: ASTM D638-14, Standard Test Method for Tensile Properties of Plastics (ASTM International, West Conshohocken, PA, 2015).Google Scholar
Doerner, M.F. and Nix, W.D.: A method for interpreting the data from depth-sensing indentation instruments. J. Mater. Res. 1, 601 (1986).CrossRefGoogle Scholar
Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564 (1992).CrossRefGoogle Scholar
Oliver, W.C. and Pharr, G.M.: Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 19, 3 (2004).CrossRefGoogle Scholar
Jeon, E.C., Baik, M.K., Kim, S.H., Lee, B.W., and Kwon, D.I.: Determining representative stress and representative strain in deriving indentation flow curves based on finite element analysis. Key Eng. Mater. 297, 2152 (2005).10.4028/www.scientific.net/KEM.297-300.2152CrossRefGoogle Scholar
Jeon, E-c., Kim, J-Y., Baik, M-K., Kim, S-H., Park, J-S., and Kwon, D.: Optimum definition of true strain beneath a spherical indenter for deriving indentation flow curves. Mater. Sci. Eng. A. 419, 196 (2006).CrossRefGoogle Scholar
Kim, S.H., Lee, B.W., Choi, Y., and Kwon, D.: Quantitative determination of contact depth during spherical indentation of metallic materials—A FEM study. Mater. Sci. Eng. A. 415, 59 (2006).CrossRefGoogle Scholar
Kang, S-K., Kim, Y-C., Kim, K-H., Kim, J-Y., and Kwon, D.: Extended expanding cavity model for measurement of flow properties using instrumented spherical indentation. Int. J. Plast. 49, 1 (2013).CrossRefGoogle Scholar
Kim, Y-C., Kang, S-K., Kim, J-Y., and Kwon, D.: Contact morphology and constitutive equation in evaluating tensile properties of austenitic stainless steels through instrumented spherical indentation. J. Mater. Sci. 48, 232 (2013).CrossRefGoogle Scholar
Kim, K-H., Kim, Y-C., Jeon, E-C., and Kwon, D.: Evaluation of indentation tensile properties of Ti alloys by considering plastic constraint effect. Mater. Sci. Eng. A. 528, 5259 (2011).CrossRefGoogle Scholar
Tabor, D.: The Hardness of Metals (Clarendon Press, Oxford, U.K., 1951); pp. 19, 94.Google Scholar
Hill, R.: The Mathematical Theory of Plasticity (Clarendon Press, Oxford, U.K., 1950); pp. 97, 106.Google Scholar
Johnson, K.: The correlation of indentation experiments. J. Mech. Phys. Solids. 18, 115 (1970).CrossRefGoogle Scholar
Gao, X-L.: Strain gradient plasticity solution for an internally pressurized thick-walled spherical shell of an elastic–plastic material. Mech. Res. Commun. 30, 411 (2003).CrossRefGoogle Scholar
Wright, S., Huang, Y., and Fleck, N.: Deep penetration of polycarbonate by a cylindrical punch. Mech. Mater. 13, 277 (1992).CrossRefGoogle Scholar
Murthy, T., Madariaga, J., and Chandrasekar, S.: Direct mapping of deformation in punch indentation and correlation with slip line fields. J. Mater. Res. 24, 760 (2009).CrossRefGoogle Scholar
Murthy, T., Gnanamanickam, E., and Chandrasekar, S.: Deformation field in indentation of a granular ensemble. Phys. Rev. E. 85, 061306 (2012).CrossRefGoogle ScholarPubMed
Ashby, M.: Indentation creep. Mater. Sci. Tech. 8, 594 (1992).Google Scholar
Lu, J., Suresh, S., and Ravichandran, G.: Dynamic indentation for determining the strain rate sensitivity of metals. J. Mech. Phys. Solids. 51, 1923 (2003).CrossRefGoogle Scholar
Riccardi, B. and Montanari, R.: Indentation of metals by a flat-ended cylindrical punch. Mater. Sci. Eng. A. 381, 281 (2004).CrossRefGoogle Scholar
Lee, C. and Kobayashi, S.: Elastoplastic analysis of plane-strain and axisymmetric flat punch indentation by the finite-element method. Int. J. Mech. Sci. 12, 349 (1970).CrossRefGoogle Scholar
Pamplona, D.C., Weber, H.I., and Sampaio, G.R.: Analytical, numerical and experimental analysis of continuous indentation of a flat hyperelastic circular membrane by a rigid cylindrical indenter. Int. J. Mech. Sci. 87, 18 (2014).CrossRefGoogle Scholar
Studman, C., Moore, M., and Jones, S.: On the correlation of indentation experiments. J. Phys. D. Appl. Phys. 10, 949 (1977).CrossRefGoogle Scholar
Yu, H., Imam, M., and Rath, B.: Study of the deformation behaviour of homogeneous materials by impression tests. J. Mater. Sci. 20, 636 (1985).CrossRefGoogle Scholar
Elleuch, R. and Taktak, W.: Viscoelastic behavior of HDPE polymer using tensile and compressive loading. J. Mater. Eng. Perform. 15, 111 (2006).CrossRefGoogle Scholar
Ognedal, A.S., Clausen, A.H., Polanco-Loria, M., Benallal, A., Raka, B., and Hopperstad, O.S.: Experimental and numerical study on the behaviour of PVC and HDPE in biaxial tension. Mech. Mater. 54, 18 (2012).CrossRefGoogle Scholar
International Organization for Standardization: ISO/FDIS 14577-1, Metallic Materials–Instrumented Indentation Test for Hardness and Materials Parameter-Part 1: Test Method (International Organization for Standardization, Geneva, 2002).Google Scholar