Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T21:33:32.423Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinetics of length-scale dependent plastic deformation of gold microspheres

Published online by Cambridge University Press:  22 June 2017

AZM Ariful Islam Open the ORCID record for AZM Ariful Islam [Opens in a new window]  and
Robert J. Klassen
AZM Ariful Islam*
Affiliation:
Department of Mechanical and Materials Engineering, Western University, London, Ontario N6A 5B9, Canada
Robert J. Klassen
Affiliation:
Department of Mechanical and Materials Engineering, Western University, London, Ontario N6A 5B9, Canada
*
a) Address all correspondence to this author. e-mail: aislam32@uwo.ca
Get access

Abstract

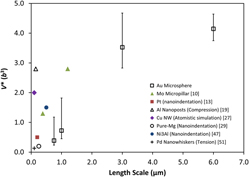
The size and strain-rate dependence of plastic deformation in Au microspheres of diameter ranging from 0.8 to 6.0 µm was investigated at room-temperature using flat-punch micro-compression testing. The contact yield stress was observed to increase with decreasing microsphere diameter. The apparent activation volume, V*, associated with the rate dependent plastic deformation remained essentially constant between 4 and 6b 3 for 0.8 and 1.0 µm spheres over strains up to 20% whereas it increased from 12 to 42b 3 for the larger 3.0 and 6.0 µm diameter specimens. The initiation of plastic deformation within the microspheres was also found to be highly dependent upon sphere diameter and strain rate with associated V*, and apparent activation energy, Q*, values of 0.4b 3 and 0.02 eV for 0.8 µm diameter spheres increasing to 4.1b 3 and 0.16 eV for 6.0 µm diameter spheres. These values indicate that initial plasticity is controlled by heterogeneous nucleation events that are consistent with a surface self-diffusion mechanism.

Keywords

Austrengthstress/strain relationship
Type
Articles
Information
Journal of Materials Research , Volume 32 , Issue 18 , 28 September 2017 , pp. 3507 - 3515
Check for updates
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Mathias Göken

References

REFERENCES

Greer, J.R., Oliver, W.C., and Nix, W.D.: Size dependence of mechanical properties of gold at the micron scale in the absence of strain gradients. Acta Mater. 53, 1821 (2005).CrossRefGoogle Scholar
Nix, W.D., Greer, J.R., Feng, G., and Lilleodden, E.T.: Deformation at the nanometer and micrometer length scales: Effects of strain gradients and dislocation starvation. Thin Solid Films 515, 3152 (2007).CrossRefGoogle Scholar
Kim, J-Y. and Greer, J.R.: Tensile and compressive behavior of gold and molybdenum single crystals at the nano-scale. Acta Mater. 57, 5245 (2009).CrossRefGoogle Scholar
Frick, C.P., Clark, B.G., Orso, S., Schneider, A.S., and Arzt, E.: Size effect on strength and strain hardening of small-scale [111] nickel compression pillars. Mater. Sci. Eng., A 489, 319 (2008).CrossRefGoogle Scholar
Uchic, M.D., Dimiduk, D.M., Florando, J.N., and Nix, W.D.: Sample dimensions influence strength and crystal plasticity. Science 305, 986 (2004).CrossRefGoogle ScholarPubMed
Purkayastha, R. and McMeeking, R.: A parameter study of intercalation of lithium into storage particles in a lithium-ion battery. Comput. Mater. Sci. 80, 2 (2013).CrossRefGoogle Scholar
Greer, J. and Nix, W.: Nanoscale gold pillars strengthened through dislocation starvation. Phys. Rev. B 73, 245410 (2006).CrossRefGoogle Scholar
Greer, J.R., Weinberger, C.R., and Cai, W.: Comparing the strength of f.c.c. and b.c.c. sub-micrometer pillars: Compression experiments and dislocation dynamics simulations. Mater. Sci. Eng., A 493, 21 (2008).CrossRefGoogle Scholar
Mook, W.M., Niederberger, C., Bechelany, M., Philippe, L., and Michler, J.: Compression of freestanding gold nanostructures: From stochastic yield to predictable flow. Nanotechnology 21, 55701 (2010).CrossRefGoogle ScholarPubMed
Schneider, A.S., Clark, B.G., Frick, C.P., and Arzt, E.: Correlation between activation volume and pillar diameter for Mo and Nb BCC Pillars. MRS Proc. 1185, 1185 (2009).CrossRefGoogle Scholar
Shenoy, V.B., Phillips, R., and Tadmor, E.B.: Nucleation of dislocations beneath a plane strain indenter. J. Mech. Phys. Solids 48, 649 (2000).CrossRefGoogle Scholar
Liu, Y., Van der Giessen, E., and Needleman, A.: An analysis of dislocation nucleation near a free surface. Int. J. Solids Struct. 44, 1719 (2007).CrossRefGoogle Scholar
Schuh, C.A., Mason, J.K., and Lund, A.C.: Quantitative insight into dislocation nucleation from high-temperature nanoindentation experiments. Nat. Mater. 4, 617 (2005).CrossRefGoogle ScholarPubMed
Paul, W., Oliver, D., Miyahara, Y., and Grütter, P.H.: Minimum threshold for incipient plasticity in the atomic-scale nanoindentation of Au(111). Phys. Rev. Lett. 110, 1 (2013).CrossRefGoogle ScholarPubMed
Mordehai, D., Lee, S-W., Backes, B., Srolovitz, D.J., Nix, W.D., and Rabkin, E.: Size effect in compression of single-crystal gold microparticles. Acta Mater. 59, 5202 (2011).CrossRefGoogle Scholar
Mordehai, D., Kazakevich, M., Srolovitz, D.J., and Rabkin, E.: Nanoindentation size effect in single-crystal nanoparticles and thin films: A comparative experimental and simulation study. Acta Mater. 59, 2309 (2011).CrossRefGoogle Scholar
Lee, S-W., Mordehai, D., Rabkin, E., and Nix, W.D.: Effects of focused-ion-beam irradiation and prestraining on the mechanical properties of FCC Au microparticles on a sapphire substrate. J. Mater. Res. 26, 1653 (2011).CrossRefGoogle Scholar
Wang, Z-J., Shan, Z-W., Li, J., Sun, J., and Ma, E.: Pristine-to-pristine regime of plastic deformation in submicron-sized single crystal gold particles. Acta Mater. 60, 1368 (2012).CrossRefGoogle Scholar
Mook, W.M., Lund, M.S., Leighton, C., and Gerberich, W.W.: Flow stresses and activation volumes for highly deformed nanoposts. Mater. Sci. Eng., A 493, 12 (2008).CrossRefGoogle Scholar
Gall, K., Diao, J., and Dunn, M. L.: The strength of gold nanowires. Nano Lett. 4, 2431 (2004).CrossRefGoogle Scholar
Weinberger, C.R., Jennings, A.T., Kang, K., and Greer, J.R.: Atomistic simulations and continuum modeling of dislocation nucleation and strength in gold nanowires. J. Mech. Phys. Solids 60, 84 (2012).CrossRefGoogle Scholar
Deng, C. and Sansoz, F.: Effects of twin and surface facet on strain-rate sensitivity of gold nanowires at different temperatures. Phys. Rev. B: Condens. Matter Mater. Phys. 81, 1 (2010).CrossRefGoogle Scholar
Kelly, A. and Nicholson, R.B.: Strengthening Methods in Crystals (Halstead Press Division, Wiley, New York, 1972).Google Scholar
Dao, M., Lu, L., Shen, Y.F., and Suresh, S.: Strength, strain-rate sensitivity and ductility of copper with nanoscale twins. Acta Mater. 54, 5421 (2006).CrossRefGoogle Scholar
Wang, Y.M., Hamza, A.V., and Ma, E.: Activation volume and density of mobile dislocations in plastically deforming nanocrystalline Ni. Appl. Phys. Lett. 86, 241917 (2005).CrossRefGoogle Scholar
Jennings, A.T., Li, J., and Greer, J.R.: Emergence of strain-rate sensitivity in Cu nanopillars: Transition from dislocation multiplication to dislocation nucleation. Acta Mater. 59, 5627 (2011).CrossRefGoogle Scholar
Zhu, T., Li, J., Samanta, A., Leach, A., and Gall, K.: Temperature and strain-rate dependence of surface dislocation nucleation. Phys. Rev. Lett. 100, 25502 (2008).CrossRefGoogle ScholarPubMed
Wang, Y., Hamza, A., and Ma, E.: Temperature-dependent strain rate sensitivity and activation volume of nanocrystalline Ni. Acta Mater. 54, 2715 (2006).CrossRefGoogle Scholar
Somekawa, H. and Schuh, C.A.: Effect of solid solution elements on nanoindentation hardness, rate dependence, and incipient plasticity in fine grained magnesium alloys. Acta Mater. 59, 7554 (2011).CrossRefGoogle Scholar
Zhu, T., Li, J., Ogata, S., and Yip, S.: Mechanics of ultra-strength materials. MRS Bull. 34, 167 (2009).CrossRefGoogle Scholar
Rodriguez, P.: Grain size dependence of the activation parameters for plastic deformation: Influence of crystal structure, slip system, and rate-controlling dislocation mechanism. Metall. Mater. Trans. A 35, 2697 (2004).CrossRefGoogle Scholar
Nix, W.D. and Lee, S.: Micro-pillar plasticity controlled by dislocation nucleation at surfaces. Philos. Mag. 91, 1084 (2011).CrossRefGoogle Scholar
Bhakhri, V. and Klassen, R.J.: The strain-rate dependence of the nanoindentation stress of gold at 300 K: A deformation kinetics-based approach. J. Mater. Res. 24, 1456 (2009).CrossRefGoogle Scholar
Kocks, U.F., Argon, A.S., and Ashby, M.F.: Thermodynamics and kinetics of slip. Prog. Mater. Sci. 19, 1 (1975).Google Scholar
Kogut, L. and Etsion, I.: Elastic–plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 69, 657 (2002).CrossRefGoogle Scholar
Maharaj, D. and Bhushan, B.: Nanomanipulation, nanotribology and nanomechanics of Au nanorods in dry and liquid environments using an AFM and depth sensing nanoindenter. Nanoscale 6, 5838 (2014).CrossRefGoogle ScholarPubMed
Heyer, J-K., Brinckmann, S., Pfetzing-Micklich, J., and Eggeler, G.: Microshear deformation of gold single crystals. Acta Mater. 62, 225 (2014).CrossRefGoogle Scholar
Kamimura, Y., Edagawa, K., and Takeuchi, S.: Experimental evaluation of the Peierls stresses in a variety of crystals and their relation to the crystal structure. Acta Mater. 61, 294 (2013).CrossRefGoogle Scholar
Hull, D. and Bacon, D.: Introduction to Dislocations, 4th ed. (Butterworth-Heinemann, Jordan Hill, Oxford, 2001).Google Scholar
Brenner, S.S.: Tensile strength of whiskers. J. Appl. Phys. 27, 1484 (1956).CrossRefGoogle Scholar
Bei, H., Shim, S., Pharr, G.M., and George, E.P.: Effects of pre-strain on the compressive stress–strain response of Mo-alloy single-crystal micropillars. Acta Mater. 56, 4762 (2008).CrossRefGoogle Scholar
Salehinia, I., Perez, V., and Bahr, D.F.: Effect of vacancies on incipient plasticity during contact loading. Philos. Mag. 92, 550 (2012).CrossRefGoogle Scholar
Orowan, E.: Problems of plastic gliding. Proc. Phys. Soc. 52, 8 (1940).CrossRefGoogle Scholar
Bhakhri, V., Wang, J., Ur-rehman, N., Ciurea, C., Giuliani, F., and Vandeperre, L.J.: Instrumented nanoindentation investigation into the mechanical behavior of ceramics at moderately elevated temperatures. J. Mater. Res. 27, 65 (2011).CrossRefGoogle Scholar
Baufeld, B., Messerschmidt, U., Bartsch, M., and Baither, D.: Plasticity of cubic zirconia between 700 °C and 1150 °C observed by macroscopic compression and by in situ tensile straining tests. Key Eng. Mater. 97–98, 431 (1994).Google Scholar
Pirouz, P., Demenet, J.L., and Hong, M.H.: On transition temperatures in the plasticity and fracture of semiconductors. Philos. Mag. A 81, 1207 (2001).CrossRefGoogle Scholar
Wo, P.C., Zuo, L., and Ngan, A.H.W.: Time-dependent incipient plasticity in Ni3Al as observed in nanoindentation. J. Mater. Res. 20, 489 (2005).CrossRefGoogle Scholar
Smith, J.F. and Zheng, S.: High temperature nanoscale mechanical property measurements. Surf. Eng. 16, 143 (2000).CrossRefGoogle Scholar
Vieregge, J.: Nanoscale Creep Testing of Copper & Gold, Hysitron Inc application note, Minneapolis, MN.Google Scholar
Liu, C.L., Cohen, J.M., Adams, J.B., and Voter, A.F.: EAM study of surface self-diffusion. Surf. Sci. 253, 334 (1991).CrossRefGoogle Scholar
Chen, L.Y., He, M., Shin, J., Richter, G., and Gianola, D.S.: Measuring surface dislocation nucleation in defect-scarce nanostructures. Nat. Mater. 14, 707 (2015).CrossRefGoogle ScholarPubMed
Li, J.: Dislocation nucleation: Diffusive origins. Nat. Mater. 14, 656 (2015).CrossRefGoogle ScholarPubMed