Article contents
Modeling nanoindentation using the Material Point Method
Published online by Cambridge University Press: 25 May 2018
Abstract
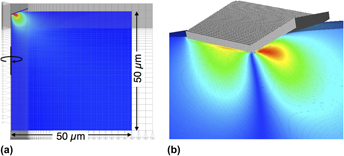
A numerical nanoindentation model was developed using the Material Point Method (MPM), which was chosen because it can handle both large deformations and dynamic contact under the indenter. Because of the importance of contact, prior MPM contact methods were enhanced to improve their accuracy for contact detection. Axisymmetric and full 3D simulations investigated the effects of hardening, strain-rate dependent yield properties, and local structure under the indenter. Convergence of load–displacement curves required small cells under the indenter. To reduce computation time, we used an effective nonregular grid, called a tartan grid and describe its implementation. Tartan grids reduced simulation times by an order of magnitude. A series of simulated load–displacement curves were analyzed as “virtual experiments” by standard Oliver–Pharr methods to extract effective modulus and hardness of the indented material. We found that standard analysis methods give results that are affected by hardening parameters and strain-rate dependence of plasticity. Because these parameters are not known during experiments, extracted properties will always have limited accuracy. We describe an approach for extracting more properties and more accurate properties by combining MPM simulations with inverse methods to fit simulation results to entire load–displacement curves.
Keywords
Information
- Type
- Article
- Information
- Copyright
- Copyright © Materials Research Society 2018
References
REFERENCES
- 11
- Cited by

