Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T08:57:07.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical modeling of centerline segregation by a combined 3-D and 2-D hybrid model during slab continuous casting

Published online by Cambridge University Press:  19 February 2018

Huabiao Chen ,
Dengfu Chen ,
Mujun Long ,
Huamei Duan ,
Yunwei Huang  and
Lintao Gui
Huabiao Chen
Affiliation:
College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China
Dengfu Chen*
Affiliation:
College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China
Mujun Long*
Affiliation:
College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China
Huamei Duan
Affiliation:
College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China
Yunwei Huang
Affiliation:
College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China
Lintao Gui
Affiliation:
College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China
*
a)Address all correspondence to these authors. e-mail: chendfu@cqu.edu.cn
b)e-mail: longmujun@cqu.edu.cn
Get access

Abstract

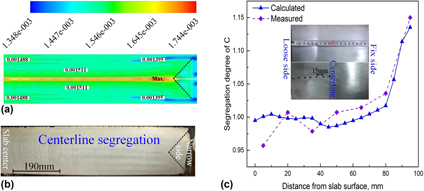
Centerline segregation is one of the typical internal defects, which occurs during slab continuous casting (CC). To investigate and predict the centerline segregation encountered in a continuously cast slab, a combined 3-D and 2-D hybrid simulation model for centerline segregation was developed. The average deviation between the calculated and experimented results reaches as low as 0.5%, which demonstrates that the hybrid simulation model has relatively high reliability. The centerline segregation of the slab was predicted accurately. The results show that macrosegregation occurring during the slab CC process has heredity. In the casting direction, the concentration of solutes in the liquid pool increases gradually until the casting has solidified completely. After complete solidification, the solutes’ concentration maintains an almost constant value. On the centerline, the maximum segregation degree occurs at a position roughly 614 mm from the slab center. The maximum centerline segregation degrees of C, Si, Mn, P, and S solutes are 1.163, 1.058, 1.045, 1.111, and 1.165, respectively.

Keywords

slab continuous castinghybrid simulation modelcenterline segregationsolute redistribution
Type
Article
Information
Journal of Materials Research , Volume 33 , Issue 8 , 27 April 2018 , pp. 989 - 1002
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Susan B. Sinnott

References

REFERENCES

Domitner, J., Wu, M.H., Kharicha, A., Ludwig, A., Kaufmann, B., Reiter, J., and Schaden, T.: Modeling the effects of strand surface bulging and mechanical softreduction on the macrosegregation formation in steel continuous casting. Metall. Mater. Trans. A 45, 1415 (2014).CrossRefGoogle Scholar
Mayer, F., Wu, M., and Ludwig, A.: On the formation of centreline segregation in continuous slab casting of steel due to bulging and/or feeding. Steel Res. Int. 81, 660 (2010).CrossRefGoogle Scholar
Fachinotti, V.D., Le Corre, S., Triolet, N., Bobadilla, M., and Bellet, M.: Two-phase thermo-mechanical and macrosegregation modelling of binary alloys solidification with emphasis on the secondary cooling stage of steel slab continuous casting processes. Int. J. Numer. Meth. Eng. 67, 1341 (2006).CrossRefGoogle Scholar
Flemings, M.C. and Nereo, G.: Macrosegregation. Part 1. Trans. Met. Soc. AIME. 239, 1449 (1967).Google Scholar
Flemings, M., Mehrabian, R., and Nereo, G.: Macrosegregation. Part 2. Trans. Met. Soc. AIME. 242, 41 (1968).Google Scholar
Mehrabian, R., Keane, M., and Flemings, M.: Interdendritic fluid flow and macrosegregation; influence of gravity. Metall. Mater. Trans. 1, 1209 (1970).CrossRefGoogle Scholar
Bennon, W.D. and Incropera, F.P.: A continuum model for momentum, heat and species transport in binary solid liquid-phase change systems. 1. Model formulation. Int. J. Heat Mass Transfer 30, 2161 (1987).CrossRefGoogle Scholar
Rad, M.T., Kotas, P., and Beckermann, C.: Rayleigh number criterion for formation of A-segregates in steel castings and ingots. Metall. Mater. Trans. A 44, 4266 (2013).CrossRefGoogle Scholar
Tu, W.T., Duan, Z.H., Shen, B.Z., Shen, H.F., and Liu, B.C.: Three-dimensional simulation of macrosegregation in a 36-ton steel ingot using a multicomponent multiphase model. JOM 68, 3116 (2016).CrossRefGoogle Scholar
Liu, D.R.: Modelling of macrosegregation in steel ingot by weakly integrated micro-macroscopic model. Int. J. Cast Metals Res. 26, 143 (2013).CrossRefGoogle Scholar
Ge, H.H., Li, J., Han, X.J., Xia, M.X., and Li, J.G.: Dendritic model for macrosegregation prediction of large scale castings. J. Mater. Process. Technol. 227, 308 (2016).CrossRefGoogle Scholar
Ebisu, Y.: A numerical method of macrosegregation using a dendritic solidification model, and its applications to directional solidification via the use of magnetic fields. Metall. Mater. Trans. B 42, 341 (2011).CrossRefGoogle Scholar
Liu, W., Xie, C., Bellet, M., and Combeau, H.: 2-Dimensional FEM modeling of macrosegregation in the directional solidification with mesh adaptation. Acta Metall. Sin. 22, 233 (2009).CrossRefGoogle Scholar
Choudhary, S.K., Ganguly, S., Sengupta, A., and Sharma, V.: Solidification morphology and segregation in continuously cast steel slab. J. Mater. Process. Technol. 243, 312 (2017).CrossRefGoogle Scholar
Ganguly, S.: Morphology and segregation in continuously cast high carbon steel billets. ISIJ Int. 47, 1759 (2007).Google Scholar
Brune, T., Kortzak, K., Senk, D., Reuther, N., and Schaperkotter, M.: A three dimensional model to characterize the centerline segregation in CC slabs. Steel Res. Int. 86, 33 (2015).CrossRefGoogle Scholar
Long, M.J. and Chen, D.F.: Study on mitigating center macro-segregation during steel continuous casting process. Steel Res. Int. 82, 847 (2011).CrossRefGoogle Scholar
Long, M.J., Dong, Z.H., Chen, D.F., Liao, Q., and Ma, Y.G.: Effect of uneven solidification on the quality of continuous casting slab. Int. J. Mater. Prod. Technol. 47, 216 (2013).CrossRefGoogle Scholar
Yang, H.L., Zhao, L.G., Zhang, X.Z., Deng, K.W., Li, W.C., and Gan, Y.: Mathematical simulation on coupled flow, heat, and solute transport in slab continuous casting process. Metall. Mater. Trans. B 29, 1345 (1998).CrossRefGoogle Scholar
Vertnik, R., Šarler, B., and Senčič, B.: Solution of macrosegregation in continuously cast billets by a meshless method. In IOP Conference Series: Materials Science and Engineering (Aachen, Netherlands, 2011); pp. 1–6.Google Scholar
Li, J., Wu, M.H., Ludwig, A., and Kharicha, A.: Simulation of macrosegregation in a 2.45-ton steel ingot using a three-phase mixed columnar-equiaxed model. Int. J. Heat Mass Transfer 72, 668 (2014).CrossRefGoogle Scholar
Ma, C., Shen, H., and Huang, T.: Centerline segregation in continuous casting billets. Tsinghua Sci. Technol. 9, 550 (2004).Google Scholar
Vušanović, I., Vertnik, R., and Šarler, B.: A simple slice model for prediction of macrosegregation in continuously cast billets. In IOP Conference Series: Materials Science and Engineering (Aachen, Netherlands, 2011); pp. 1–6.Google Scholar
Aboutalebi, M.R., Hasan, M., and Guthrie, R.I.L.: Coupled turbulent-flow, heat, and solute transport in continuous-casting processes. Metall. Mater. Trans. B 26, 731 (1995).CrossRefGoogle Scholar
Sun, H.B. and Zhang, J.Q.: Study on the macrosegregation behavior for the bloom continuous casting: Model development and validation. Metall. Mater. Trans. B 45, 1133 (2014).CrossRefGoogle Scholar
Chen, H., Long, M., Cao, J., Chen, D., Liu, T., and Dong, Z.: Phase transition of peritectic steel Q345 and its effect on the equilibrium partition coefficients of solutes. Metals 7, 288 (2017).CrossRefGoogle Scholar
Launder, B.E. and Spalding, D.B.: The numerical computation of turbulent flows. Comput. Meth. Appl. Mech. Eng. 3, 269 (1974).CrossRefGoogle Scholar
Long, M.J., Chen, D.F., Wang, Q.X., Luo, D.H., Han, Z.W., Liu, Q., and Gao, W.X.: Determination of CC slab solidification using nail shooting technique. Ironmaking Steelmaking 39, 370 (2012).CrossRefGoogle Scholar
Matsumiya, T., Kajioka, H., Mizoguchi, S., Ueshima, Y., and Esaka, H.: Mathematical-analysis of segregations in continuously-cast slabs. Trans. Iron Steel Inst. Jpn. 24, 873 (1984).CrossRefGoogle Scholar
Meng, Y.A. and Thomas, B.G.: Heat-transfer and solidification model of continuous slab casting: CON1D. Metall. Mater. Trans. B 34, 685 (2003).CrossRefGoogle Scholar
Won, Y.M. and Thomas, B.G.: Simple model of microsegregation during solidification of steels. Metall. Mater. Trans. A 32, 1755 (2001).CrossRefGoogle Scholar