Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T15:42:14.208Z Has data issue: false hasContentIssue false
  • English
  • Français

On the design of 1–3 piezocomposites using topology optimization

Published online by Cambridge University Press:  31 January 2011

O. Sigmund ,
S. Torquato  and
I. A. Aksay
O. Sigmund
Affiliation:
Departments of Civil Engineering and Operations Research and Chemical Engineering, Princeton Materials Institute, Princeton University, Princeton, New Jersey 08544
S. Torquato
Affiliation:
Departments of Civil Engineering and Operations Research and Chemical Engineering, Princeton Materials Institute, Princeton University, Princeton, New Jersey 08544
I. A. Aksay
Affiliation:
Departments of Civil Engineering and Operations Research and Chemical Engineering, Princeton Materials Institute, Princeton University, Princeton, New Jersey 08544
Get access

Abstract

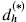We use a topology optimization method to design 1–3 piezocomposites with optimal performance characteristics for hydrophone applications. The performance characteristics we focus on are the hydrostatic charge coefficient , the hydrophone figure of merit 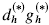, and the electromechanical coupling factor 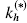. The piezocomposite consists of piezoelectric rods embedded in an optimal polymer matrix. We use the topology optimization method to design the optimal (porous) matrix microstructure. When we design for maximum 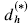and 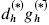, the optimal transversally isotopic matrix material has negative Poisson's ratio in certain directions. When we design for maximum 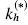, the optimal matrix microstructure is layered and simple to build.

Type
Articles
Information
Journal of Materials Research , Volume 13 , Issue 4 , April 1998 , pp. 1038 - 1048
Copyright
Copyright © Materials Research Society 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Newnham, R. E. and Ruchau, G. R., J. Am. Ceram. Soc. 74, 463 (1991).CrossRefGoogle Scholar
2.Smith, W. A., in Proceedings of IEEE Ultrasonics symposium (IEEE, 1991).Google Scholar
3.Newnham, R. E., Ferroelectrics 68, 1 (1986).CrossRefGoogle Scholar
4.Klicker, K. A., Biggers, J. V., and Newnham, R. E., J. Am. Ceram. Soc. 64, 5 (1991).CrossRefGoogle Scholar
5.Ting, R. Y., Shaulov, A. A., and Smith, W. A., Ferroelectrics 132, 69 (1992).CrossRefGoogle Scholar
6.Chan, H. L. W. and Unsworth, J., IEEE, Trans. Ultrasonic Ferroelectrics in Frequency Control 36, 434 (1989).CrossRefGoogle Scholar
7.Avellaneda, M. and Swart, P. J., unpublished.Google Scholar
8.Gibiansky, L. V. and Torquato, S., J. Mech. Phys. Solids (in press, 1997).Google Scholar
9.Milton, G. W. and Cherkaev, A. V., J. Eng. Mater. Technol., Trans. ASME 117, 483 (1995).CrossRefGoogle Scholar
10.Vigdergauz, S. B., Mech. Solids 24, 57 (1989).Google Scholar
11.Grabovsky, Y. and Kohn, R. V., J. Mech. Phys. Solids 43, 949 (1995).CrossRefGoogle Scholar
12.Sigmund, O., Ph.D. Thesis, Department of Solid Mechanics, Technical University of Denmark, 1994).Google Scholar
13.Sigmund, O., Int. J. Solids Struct. 31, 2313 (1994).CrossRefGoogle Scholar
14.Sigmund, O., Mech. Mater. 20, 351 (1995).CrossRefGoogle Scholar
15.Bendsøe, M. P. and Kikuchi, N., Comput. Methods in Appl. Mech. Eng. 71, 197 (1988).CrossRefGoogle Scholar
16.Cherkaev, A. and Palais, R., unpublished.Google Scholar
17.Allaire, G., Bonnetier, E., Francfort, G., and Jouve, F., unpublished.Google Scholar
18.Lipton, R. and Díaz, A. R., in First World Congress on Structural and Multidisciplinary Optimization, edited by Rozvany, G. I. N. and Olhoff, (N. Pergamon, Goslar, Germany, 1995), pp. 161–168.Google Scholar
19.Bourgat, J. F., Lecture Notes in Mathematics (Springer-Verlag, Berlin, 1997), pp. 330–356.Google Scholar
20.Guedes, J. M. and Kikuchi, N., Computer Methods Appl. Mech. Eng. 83, 143 (1991).CrossRefGoogle Scholar
21.Pedersen, P., in AGARD Conference Proceedings No. 36, Symposium on Structural Optimization (1970), pp. 189–192.Google Scholar
22.Schittkowski, K., Struct. Optimization 7, 1 (1994).CrossRefGoogle Scholar
23.Sigmund, O. and Torquato, S., J. Mech. Phys. Solids 45, 1037 (1997).CrossRefGoogle Scholar
24.Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P., Numerical Recipes in Fortran (Cambridge University Press, England, 1992).Google Scholar
25.Hollister, S. R. and Riemer, B. A., in SPIE, volume 2035, Mathematical Methods in Medical Imaging II (1993), pp. 95–106.Google Scholar
26.Hanson, R. J. and Hiebert, K. L., Technical Report No. SAND81–0297, Sandia National Laboratories (unpublished).Google Scholar
27.Jog, C. S. and Haber, R. B., Computer Methods Appl. Mech. Eng. 130, 203 (1996).CrossRefGoogle Scholar
28.Díaz, A. R. and Sigmund, O., Struct. Optimization 10, 40 (1995).CrossRefGoogle Scholar
29.Sigmund, O., Mech. Struct. Machines 25, 495 (1997).CrossRefGoogle Scholar
30.Almgren, R. F., J. Elast. 12, 839 (1985).Google Scholar
31.Kolpakov, A. G., PMM J. Appl. Math. Mech., U.S.S.R. 49, 739 (1985).CrossRefGoogle Scholar
32.Sigmund, O., in Proceedings of the Third International Conference on Intelligent Material, ICIM96, Lyon, June, edited by Gobin, P. (SPIE vol. 2779, 1996).Google Scholar
33.Jacobs, P., Rapid Prototyping and Manufacturing–Fundamentals of Stereolithography (SME, Dearborn, MI, 1992).Google Scholar
34.Griffith, M. L. and Halloran, J. W., J. Am. Ceram. Soc. 79, 2601 (1996).CrossRefGoogle Scholar
35.Garg, R., Prud'homme, R. K., Aksay, I. A., Liu, F., and Alfano, R., J. Opt. Soc. Am. (in press).Google Scholar
36.Garg, R.et al., unpublished.Google Scholar
37.Larsen, U. D., Sigmund, O., and Bouwstra, S., J. Microelectromechanical Systems, 6, 99 (1997).CrossRefGoogle Scholar
38.Sigmund, O. and Torquato, S., Appl. Phys. Lett. 69, 3203 (1996).CrossRefGoogle Scholar