I. INTRODUCTION
The past decade has seen a number of revolutionary advances in the available characterization toolbox:
• Conventional plane-section microscopy techniques, including optical and scanning electron microscopy (SEM), have been synergized with automated methods of serial sectioning, providing rapid access to full three-dimensional (3D) views of complex microstructures.Reference Lund and Voorhees1–Reference Inkson, Olsen, Norris, O’Neill and Möbus3
• Crystallographic orientation information can now be mapped spatially in 3D because of the advances in synchrotron x-ray and neutron diffraction methodsReference Larson, Wang, Ice, Budai and Tischler4–Reference King, Johnson, Engelberg, Ludwig and Marrow7 and electron backscattering diffraction (EBSD) in combination with serial sectioning technologies.Reference Uchic, Groeber, Dimiduk and Simmons8–Reference Wilkinson, Meaden and Dingley16
• Tomographic methods using x-rays have become available ubiquitously and are achieving finer resolution.Reference Larson, Wang, Ice, Budai and Tischler4, Reference Suter, Hefferan, Li, Hennessy, Xiao, Lienert and Tieman6, Reference Poulsen17–Reference Liu, Ice, Larson, Yang, Tischler and Budai19 In parallel, electron tomography techniques in the transmission electron microscope (TEM) are reaching the status of a routine capability for studies on both soft and hard materials.Reference McEwen, Renken, Marko and Mannella20, Reference Midgley and Dunin-Borkowski21
• Electron microscopy has been revolutionized through several parallel developments, including advances in in-situ testing and instrumentation,Reference Ferreira, Stach and Mitsuishi22 the application of aberration correction to improve image resolution,Reference Hetherington23–Reference Smith and Dahmen27 and the development of ultra-fast microscopy methods with unprecedented time-resolved observational capabilities.Reference Chergui and Zewail28, Reference Reed, Armstrong, Browning, Campbell, Evans, LaGrange and Masiel29
• Chemical mapping using atom probe tomography (ATP) has achieved a field-of-view spanning hundreds of millions of atomsReference Kelly and Miller30, Reference Miller31 and commensurate with the scales of very large atomistic simulations.
When taken independently, these developments are each, in their own right, major advances; they are of specific importance to the sub-community of scientists who developed them. However, when taken together, these advances foreshadow a time when the structure of a material as well as its evolution can be measured completely and specified quantitatively. For length scales spanning from the atom to macroscopic engineering components (comprising many grains and phases) and for time scales ranging from the sub-picosecond range (characteristic of phonons and electronic processes) to the microsecond range (characterizing phase transformations) and beyond, it is now possible to envision an age where a complete knowledge of material structure as well as its evolution will be available. Furthermore, these advances bring convergence in the spatial and temporal domains that are explored by simulations and experiments, making it possible for the first time to exploit the potential of both approaches fully.
This review summarizes the discussions and thoughts of a group of developers, practitioners, and customers of advanced material characterization techniques on the present status and future prospects for characterizing materials in “four-dimensions (4D)”, that is, in three spatial dimensions along with a time-resolved view of structure evolution. In addition to framing the state-of-the-art in the various characterization techniques, the group debated on the following:
(i) Future advances in techniques and identifying major roadblocks to such advances
(ii) Elaborating the most fruitful synergies among available characterization tools and strategies to further synergize these techniques in the immediate future
(iii) Identifying “grand challenge” problems in characterizing microstructure and microstructural damage evolution in materials, which pose major scientific and engineering difficulties and could be addressed and solved with the proper combination of advanced characterization tools.
Although there have been many recent conferences, symposia, and focused journal issues that have highlighted characterization advances (see, e.g., Refs. 13, Reference Clark, Ferreira and Robertson32–Reference Seidman:38), this report is differentiated by its specific focus on anticipating future needs and challenges as in points [(i)–(iii)] above. Thus, the goal of this study is to not only frame the current state of material characterization in 4D (temporal and three spatial dimensions) but also plot its future trajectory. Because the group involved only a small cross-section of the community, the topical coverage in this article is by no means exhaustive or even homogeneous. It is, rather, a viewpoint: a reflection of the opinions and findings of this group developed through their review and discussion.
This paper is organized as follows:
• Section II provides a brief survey of recent characterization advances. In addition, it presents the prospects for technique and instrumentation development and refinement and highlights the urgent needs.
• Section III provides examples of current synergies among the various characterization techniques reviewed in Sec. II, which foreshadow the dramatic advances that will be enabled by this advanced characterization toolbox.
• Section IV presents suggestions for specific grand challenge problems that should be addressed in a holistic way by using the proper combination of characterization tools.
• Section V summarizes the major conclusions.
II. MATERIAL CHARACTERIZATION TECHNIQUES: RECENT ADVANCES AND FUTURE EXPECTATIONS
This report was inspired by the many parallel and revolutionary advances that have occurred throughout the material characterization community in the past decade or so. The first task was to review the most significant of these developments and to establish expectations for future advances in characterization techniques. This section reviews the outcome of that discussion briefly. This section is not intended to be a rigorous technical review of these techniques, but a high-level overview of the extant capabilities with references to detailed literature for the readers. The following sections are organized loosely by length scale, beginning with TEM-based techniques and ATP, proceeding to analysis methods using x-ray and neutron sources, and concluding with large field-of-view methods based on plane-section microscopy and serial sectioning.
A. Towards 3D characterization in TEM
The electron microscope has become a standard tool for the characterization of materials, providing snapshots of microstructure and composition, enabling phase identification, and providing crystallographic information, as well as insight into properties such as the electronic and magnetic states and structure. For example, the bright-field diffraction contrast image presented in Fig. 1 yields information about the dislocation structure around a crack tip in Si,Reference Tanaka, Sadamatsu, Nakamura, Higashida, Liu and Robertson39 but it also highlights two significant limitations of the information contained in such micrographs. First, the information is two-dimensional (2D). Most of the spatial information in the direction of the electron beam is lost, and consequently, the dislocation geometry and its relationship to the crack cannot be discerned from the image. Some depth information can be obtained from pairs of stereographic images taken at different tilt angles and then fused by the human brain with the aid of, for example, a stereoscope or red-blue anaglyphs. However, these methods lack the flexibility of an arbitrary viewing direction and the depth information is difficult to quantify and to present. Second, the micrograph conveys no information about how the dislocation arrangement evolved as a function of deformation history. This latter issue reflects the fact that most TEM information is gained post-mortem, after processing, fabrication, and testing, and such images are subsequently used to infer the relationship between the observed state and the route and processes by which it was attained. While the ability to observe the evolution of microstructure has always been possible in the electron microscope, the range of stimuli and measurement probes that could be used were limited and the temporal resolution was at best 0.03 s.

FIG. 1. Bright-field transmission electron microscopy (TEM) image of the dislocation structure around a crack tip in Si. The diffraction vector was g = 220 and the foil orientation [001]. From Ref. Reference Tanaka, Sadamatsu, Nakamura, Higashida, Liu and Robertson39. Copyright Elsevier, reproduced with permission.
Over the past few decades, there have been numerous advances in instrumentation for the TEM. Advances have been made in sphericalReference Hetherington23, Reference Krivanek, Corbin, Dellby, Elston, Keyse, Murfitt, Own, Szilagyi and Woodruff24, Reference Haider, Rose, Uhlemann, Kabius and Urban40–Reference Haider, Rose, Uhlemann, Schwan, Kabius and Urban42 and chromaticReference Haider, Müller, Uhlemann, Zach, Loebau and Hoeschen43 aberration correctors, monochromators,Reference Hetherington23, Reference Krivanek, Corbin, Dellby, Elston, Keyse, Murfitt, Own, Szilagyi and Woodruff24, Reference Rose41–Reference Kabius and Rose44 electron sources,Reference Baum and Zewail45, Reference LaGrange, Armstrong, Boyden, Brown, Campbell, Colvin, DeHope, Frank, Gibson, Hartemann, Kim, King, Pyke, Reed, Shirk, Shuttlesworth, Stuart, Torralva and Browning46 electron lenses,Reference Hilbert, Uiterwaal, Barwick, Batelaan and Zewail47 sample holders,48 and microlithography processed–samples that incorporate the sample, stimulate it, and measure its macroscopic response in situ,Reference Haque and Saif49–Reference Espinosa, Zhu and Moldovan51 as well as detectors and image processing software.52 These developments have not just advanced the spatial resolution such that it is now below 0.7 × 10−10 m and element sensitive but have transformed the electron microscope from a static 2D tool to one that is capable of providing time-resolved, 3D structural, compositional, electronic, and magnetic information. Here we review these developments with primary emphasis on nonbiological systems, although similar advances in instrumentation and technique development have enabled significant progress in that field (see, e.g., Refs. Reference McEwen, Renken, Marko and Mannella20, Reference Frank53–Reference McEwen and Marko56). The next section describes the developments that have extended conventional electron microscopy from 2D to 3D. The following one discusses the advances in instrumentation, sample holders, and sample fabrication technologies that enable probing of reactions and interactions in temporal space from the femtosecond to hundreds of seconds to be conducted.
1. Electron tomography: Extending structural and compositional imaging from 2D to 3D
Over the past decade, electron tomography has become an established technique for characterizing materials in 3D in the TEM. The technique, which has been used in the life sciences since the 1960s,Reference Frank53–Reference McEwen and Marko56 involves acquiring images of a region of interest over a large angular range and subsequently using reconstruction and visualization algorithms to obtain a 3D representation of the object. Depending on the material being examined, images for electron tomography may be acquired using bright-field, dark-field, or annular dark-field imaging, energy-loss imaging, energy-dispersive x-ray spectroscopy, or other techniques such as off-axis electron holography. The final reconstruction of the object can be used to provide information about the positions, orientations, and morphologies of nanoparticles,Reference Batenburg, Bals, Sijbers, Kubel, Midgley, Hernandez, Kaiser, Encina, Coronado and Van Tendeloo57–Reference Arslan, Yates, Browning and Midgley63 variations in density and composition,Reference Mobus and Inkson60, Reference Weyland, Midgley and Thomas64, Reference Gontard, Dunin-Borkowski, Chong, Ozkaya and Midgley65 the positions of defects such as dislocations,Reference Barnard, Sharp, Tong and Midgley66–Reference Tanaka, Higashida, Kaneko, Hata and Mitsuhara69 and even electromagnetic fields.Reference Phatak, Beleggiab and Graef70–Reference Phatak, Tanase, Petford-Long and De Graef72
There are numerous requirements in acquiring the images used to create tomograms: the contrast should vary monotonically (ideally linearly) with specimen thickness and with a parameter such as density or composition; the tilt increment between images should be as small as possible, usually 0.5° to 1°; the angular range over which images are acquired should be as large as possible and at least −70° to 70°; and misalignments between successive images should be minimized before reconstruction. Clearly, these are demanding requirements not only in terms of image quality and alignment but also in terms of the volume of data generated. The reconstructed 3D volume is formed by using either a weighted back-projection schemeReference Baumeister73 or iterative reconstruction algorithms.Reference McEwen, Renken, Marko and Mannella20
The angular range requirement is a significant issue as full specimen rotation is not always possible due to the magnitude of the pole-piece gap of the objective lens in comparison to the thickness of the sample holder. In addition, rotation of a planar TEM sample beyond about 70° leads to an oblique incident angle at which the sample may no longer be electron transparent. If the angular range used is too small, significant artifacts may be present in the reconstruction–these can be described in terms of a “missing wedge” of information in Fourier space, as each projected image provides information only about a single central slice in the Fourier space representation of the object. The concept of the “missing wedge” and the impact it has on the detail in the reconstructed image are illustrated in Fig. 2, which shows how the angular range and the number of images used impact the quality of the reconstruction.Reference Midgley and Weyland74 Although the influence of the missing wedge on the quality of the reconstructed image can be minimized by acquiring orthogonal or conical tilt series of images, the use of such schemes compounds the problem of acquiring and aligning images, especially if diffraction contrast imaging conditions are used.Reference Arslan, Tong and Midgley75

FIG. 2. (a) Illustration of the nonuniform sampling of Fourier space brought about by the acquisition of a tilt series. If a simple back-projection is performed, then the relatively large number of data points at low frequencies results in a blurred reconstruction; (b) two-dimensional (2D) test object; (c) illustration of the effect on reconstructed image of increasing tilt range (shown in the lower left corner of each image); (d) illustration of the effect on increasing the number of images (number given in the lower right corner of each image). Adapted from Ref. Reference Midgley and Weyland74
a. Examples of the application of electron tomography
The signal that has been identified as most suitable for electron tomography of inorganic materials is high-angle annular dark-field (HAADF) imaging in the scanning TEM (STEM). This imaging mode is less sensitive to diffraction contrast than conventional bright-field or dark-field dynamical and kinematical imaging conditions, and it provides information that is sensitive to variations in atomic number Z (it is approximately proportional to Z 1.7). There are now many examples in the literature on the application of HAADF STEM tomography, notably to problems in heterogeneous catalysisReference Ward, Yates, Fernandez, Vaughan and Midgley61, Reference Arslan, Walmsley, Rytter, Bergene and Midgley76–Reference Yoshida, Ikuhara, Takahashi, Hirayama, Saito, Sueda, Tanaka and Gai80 and to the characterization of the morphologies of nanoparticles, nanostructures, and polymers.Reference Tanaka, Sadamatsu, Nakamura, Higashida, Liu and Robertson39, Reference Batenburg, Bals, Sijbers, Kubel, Midgley, Hernandez, Kaiser, Encina, Coronado and Van Tendeloo57, Reference Midgley, Weyland, Yates, Dunin-Borkowski and Laffont59, Reference Mobus and Inkson60, Reference Weyland, Yates, Dunin-Borkowski, Laffont and Midgley81, Reference Ortalan, Herrera, Morgan and Browning82
An example of HAADF STEM tomography is provided in the work of Cervera Gontard et al.,Reference Gontard, Dunin-Borkowski and Ozkaya83 who studied Pt and PtCr nanoparticles supported on carbon black; such materials are used as heterogeneous catalysts in the electrodes of proton exchange membrane fuel cells. Figure 3(a) shows an HAADF STEM image of Pt particles acquired at a single viewing angle; the result when a tilt series comprising 136 images is used to provide a 3D reconstruction of the particles alone is shown in Fig. 3(b). Although there are difficulties associated with reconstructing heavy particles and a light support simultaneously, such data, when processed and segmented, permit not only a clear 3D view of the two phases comprising the material (carbon black and metallic nanoparticles) as shown in Fig. 3(c), but also permit the study of minute features of individual nanoparticles, including facet geometries, surface ledges, and twins [Fig. 3(d)]. Particles as small as 5 nm were found to be amenable to 3D shape analysis, with a spatial resolution of ∼1 nm in all 3D.

FIG. 3. High-angle annular dark-field (HAADF) scanning TEM (STEM) imaging of Pt and PtCr catalyst particles supported on carbon black. (a) single HAADF image of Pt features, (b) reconstructed volume, (c) three-dimensional (3D) perspective view of a full structure showing PtCr catalyst particles on carbon black. (d) Close examination of an individual Pt particle showing individual crystallographic facets. For (a,b), the tilt range was from −70° to +66°, with images acquired in 1° increments. From Ref. Reference Gontard, Dunin-Borkowski and Ozkaya83. Copyright John Wiley and Sons, reproduced with permission.
Compositional information can be obtained in the electron microscope by using either electron energy-loss spectroscopy (EELS) or energy-dispersive x-ray spectroscopy. Coupling these techniques with the acquisition of an angular tilt series allows direct determination of variations in composition in 3D.Reference Weyland, Yates, Dunin-Borkowski, Laffont and Midgley81 For example, Jarausch et al.Reference Jarausch, Thomas, Leonard, Twesten and Booth84 combined electron tomography with EELS and with information from the shape of the core-loss edge of the Si L23 peak to generate not only a 3D compositional map, but also a map of the chemical state, making up the different Si-containing phases of a W–Si contact. Examples of these maps are shown in Fig. 4.

FIG. 4. (a) Composite image of a W-to-Si contact showing the volumetric elemental distribution maps for Ti, N, and Co and (b) 3D chemical state map extracted from the shape of the core-loss edge of the Si L23 peak. From Ref. Reference Jarausch, Thomas, Leonard, Twesten and Booth84. Copyright Elsevier, reproduced with permission.
Subtle features in EELS, such as the energies of plasmon peaks, can be used to obtain 3D information about materials, in which variations in density and composition are too small to be mapped reliably using other TEM methods. For example, Yurtserver et al.Reference Yurtsever, Weyland and Muller85 combined electron tomography with plasmon-loss imaging to reconstruct silicon nanoparticles embedded in an amorphous SiO2 matrix (Fig. 5). By using this approach, they demonstrated that the dominant form of the Si nanoparticles is not the spherical shape that is normally assumed, but rather a complex morphology with a high surface-to-volume ratio. The ability to acquire images over a range of energy losses at every specimen tilt angle may alternatively allow full spectroscopic information to be acquired from each voxel in the reconstruction of an object.Reference Batenburg, Bals, Sijbers, Kubel, Midgley, Hernandez, Kaiser, Encina, Coronado and Van Tendeloo57

FIG. 5. Electron tomographic reconstruction from a series of plasmon loss images of silicon nanoparticles embedded in silicon oxide. The nanoparticles are revealed by isosurface rendering with the reconstructed plasmon loss image shown as the background fog. From Ref. Reference Yurtsever, Weyland and Muller85. Copyright AIP, reproduced with permission.
Intensity variations in diffraction contrast images and the difficulty of maintaining constant imaging conditions over a large angular range (i.e., the same diffraction vector with the same Bragg deviation parameter) make it challenging to use such an imaging condition as the basis for tomographic reconstruction. Nevertheless, several groups have reported reconstructions based on diffraction contrast imaging conditions using two-beam, weak-beam dark-field and annular dark-field imaging modes.Reference Seidman:38, Reference Barnard, Sharp, Tong and Midgley66–Reference Tanaka, Higashida, Kaneko, Hata and Mitsuhara69, Reference Kaneko, Nagayama, Inoke, Noguchi and Horita86, Reference Tanaka, Honda, Mitsuhara, Hata, Kaneko and Higashida87 An example of this capability is demonstrated in Fig. 6, in which snapshots taken from the tomogram of the dislocation structure in Fig. 1 are presented in negative form.Reference Seidman:38 For the reconstruction, images were acquired every 1° over an angular range from −43° to 31°. To assist in the visualization of the dislocation structure and to compensate for the missing wedge effect, which results from the limited angular range used, a 3D model of the dislocation configuration was constructed from the tomogram. In addition, a Thompson’s tetrahedron was positioned accurately in the model such that it becomes an integral component of it.Reference Liu and Robertson88 Snapshots of the dislocation structure rotated about orthogonal axes are shown in Figs. 6(b) and 6(c). The partitioning of the dislocations to well-defined slip bands is evident. Dislocations can be seen terminating on the crack flank as well as on the free surface, and the assignment of the dislocation line directions and slip systems becomes trivial. By combining this information with the knowledge of the Burgers vector of the dislocations, rapid determination of the properties of the dislocations becomes possible. Availability of such information will enhance our ability to unravel dislocation structures such as in dislocation forests, cross-slip processes, spatial arrangements of dislocation sources, and dislocation interactions with other obstacles. This information will yield new insight to the fundamental processes governing mechanical properties and will inform physically based models designed to assess mechanical properties. Conventional dark-field imaging has also been used to obtain the 3D morphologies of precipitates in a superalloy for which the extinction distance of the reflection used was sufficiently large when compared with the thickness of the specimen.Reference Hata, Kimura, Gao, Matsumura, Doi, Moritani, Barnard, Tong, Sharp and Midgley89

FIG. 6. 3D view of dislocations near a crack tip in silicon: (a) snapshots of the reconstructed volume; the image is the negative of that shown in Fig. 1. (b) and (c) Snapshots about orthogonal rotational axes of dislocations in reconstructed volume. Images courtesy of G. Liu, after work in Ref. Reference Seidman:38.
The TEM also affords the ability to obtain information about the magnetic-domain structures and magnetic domain walls. Traditionally, information about electromagnetic fields in and around materials has been obtained in the TEM by using the Foucault and Fresnel modes of Lorentz microscopy, respectively. 3D images of the magnetic induction in and around a magnetic sample can be obtained from the change in phase shift of the electron wave recorded at different specimen angles. This information can be acquired from either the transport-of-intensity formalism or electron holographic observations.Reference Phatak, Graef, Petford-Long, Tanase and Imre71, Reference Phatak, Tanase, Petford-Long and De Graef72, Reference Lade, Paganin and Morgan90–Reference Stolojan, Dunin-Borkowski, Weyland and Midgley92 As an example, Phatak et al.Reference Phatak, Humphrey, Graef and Petford-Long91 acquired a three-image through-focus series about orthogonal tilt axes (−70 to +70, in 5° increments) of bilayers of Py(27 nm)/Cr(3 nm) that had been patterned lithographically into various shapes. The sample was then turned over, and two additional tilt series were acquired to separate the magnetic contribution to the phase shift from that of the mean inner potential. Figures 7(a)-7(c) shows a representative through-focus series of images of an ellipsoidal particle with two magnetic vortices. Figure 7(d) shows the experimentally reconstructed 3D magnetic vector potential.

FIG. 7. A 3D reconstruction of the magnetic field of NiFe(27 nm)/Cr(3 nm). (a)-(c) Through-focus series showing a series of an elliptical particle. (d) 3D magnetic vector potential along the x-z plane of the element displayed as a vector field plot. The colors describe the z component of the vector potential. From Ref. Reference Phatak, Humphrey, Graef and Petford-Long91. Copyright Cambridge Journals, reproduced with permission.
b. Future prospects for electron tomography
The above applications of electron tomography demonstrate that it is now possible to obtain 3D structural, electronic, compositional, and magnetic information with a spatial resolution that is often around 1 nm.Reference Arslan, Yates, Browning and Midgley63 The spatial resolution of the reconstructed images are usually limited by artifacts resulting from the use of a limited angular range, from nonlinearity of the recorded signal with specimen thickness, and from the low signal-to-noise ratio in spectroscopic images. The use of a single threshold value to define an iso-surface in the reconstruction of an object, for example, a precipitate, may result in an incorrect 3D representation of the object, particularly if the particles overlap. In addition, the need to acquire images every degree over an angular range of 140° represents a major limitation. There have been numerous advances to address these challenges, some of which are described briefly here.
One advance is the use of improved reconstruction algorithms such as discrete intensity tomography, which incorporates known information about the specimen to constrain the reconstruction. For example, earlier knowledge that there are only a few phases of known densities,Reference Batenburg, Bals, Sijbers, Kubel, Midgley, Hernandez, Kaiser, Encina, Coronado and Van Tendeloo57, Reference Bals, Batenburg, Liang, Lebedev, Van Tendeloo, Aerts, Martens and Kirschhock93 or that the image is composed of only a few types of atoms arranged on a lattice,Reference Jinschek, Batenburg, Calderon, Kilaas, Radmilovic and Kisielowski94 enables the missing regions in the Fourier space of the object to be populated more correctly. In such cases, reconstruction can be performed from fewer images. For example, Batenburg et al. showed that it was possible to reconstruct the morphology of gold nanoparticles by using only 15 images.Reference Batenburg, Bals, Sijbers, Kubel, Midgley, Hernandez, Kaiser, Encina, Coronado and Van Tendeloo57 This advance foreshadows the significant improvements in efficiency that may be gained by synergizing electron tomography with other analysis methods that can be used to provide additional information about the structure.
Other advances pertain to the development of improved hardware and both reconstruction and software dedicated to optimizing electron tomography. For example, a significant advance in reconstruction algorithms would utilize the actual variation in the recorded signal with sample thickness and orientation, using input taken from models and simulations of the expected contrast from the specimen (including the effect of dynamical diffraction). The development of new specimen holder technologies allows a greater specimen tilt range to be achieved; for example, through the use of dual-axis tilting or the rotation of needle-shaped specimens by a full 360°.Reference Arslan, Tong and Midgley75, Reference Tong, Arslan and Midgley95 The use of triple axes tilting now allows for a diffracting condition to be chosen and maintained accurately as the specimen is tilted. Software that can efficiently pre-process images before reconstruction would reduce artifacts in the reconstruction, whereas improved approaches for the segmentation of phases or features could provide a representation of the object that is consistent with the original dataset.Reference Batenburg and Sijbers96, Reference Batenburg and Sijbers97
The examples that have been presented in this section all provided nanometer scale information about the materials. However, there are efforts towards the development of atomic resolution electron tomography.Reference Saghi, Xu and Mobus98, Reference Bar Sadan, Houben, Wolf, Enyashin, Seifert, Tenne and Urban99 For example, Bar Sadan et al.,Reference Bar Sadan, Houben, Wolf, Enyashin, Seifert, Tenne and Urban99 used a combination of low accelerating voltage and negative spherical aberration imaging to obtain atomic scale (∼0.2 nm) tomographic images of individual inorganic fullerene-like particles. Other approaches for imaging individual atoms in 3D have involved triangulating their positions by acquiring atomic-resolution HAADF images of a similar region of a specimen from multiple well-defined directions.Reference Yoshida, Ikuhara, Takahashi, Hirayama, Saito, Sueda, Tanaka and Gai80
At present, most electron tomograms are generated from images acquired over a large angular range at room temperature. The reconstructed images are snapshots in time of the composition or structure, albeit now in 3D. However, significant strides are being made to enable the coupling of electron tomography with in situ experimental capabilities. For this combination to become practical, it will be essential to be able to use nosier data sets as well as fewer images in the reconstruction. Longer-term directions may involve the development of instruments that allow images of materials to be acquired from two or more different directions simultaneously. The development of such capabilities is key to understanding the dynamics of processes such as dislocation nucleation and motion, and chemical reactions, phase domain growth and coarsening, as well as sintering phenomena in 3D.
There are many other possible advances in electron tomography that would find a receptive field of use across the physical sciences. A particularly valuable development would be a technique to map variations in crystallography and lattice strain in 3D. Instrumentation that allows the crystallographic orientation of a specimen to be adjusted automatically during the acquisition of a tilt series of images would be useful for the characterization of defects.
2. Time-resolved studies in the TEM
From its beginnings, the TEM has been used to study the dynamics and kinetics of reactions and processes. Critical considerations for time-resolved experiments are the spatial and temporal resolution that can be achieved and the mechanism used to excite or stimulate the material. These topics are reviewed in turn in the following two sections, which also provide examples of the use of time-resolved TEM for specific problems. The prospects for future advances in this area are then highlighted.
a. Spatial and temporal resolution
The spatial resolution in any time-resolved TEM experiment is defined by the microscope optics and the stability/environment of the stage. With current state-of-the-art spherical aberration–corrected instruments, sub-Ångström spatial resolution can be attained.Reference Freitag and Kisielowski100 Future developments will see instruments corrected for both chromatic and spherical aberration, and these will yield an order of magnitude improvement in the spatial resolution of certain classes of energy-filtered TEM images.Reference Haider, Müller, Uhlemann, Zach, Loebau and Hoeschen43 The application of these instruments to time-resolved studies is just commencing, and new avenues of research will be created as appropriate instrumentation is developed and becomes accessible.
The temporal limitation on in situ studies results from the total electron beam current and is of the order of 10 ms in a conventional electron microscope equipped with a thermionic or field emission electron source. In a practical sense, the temporal resolution is set not by the beam current but by other parameters. In the earliest studies, the temporal resolution was a few minutes and was dominated by the time to transport the recording medium in and out of the camera system. Temporal resolution was improved when cine cameras were used to record events occurring on the viewing screen, but the spatial resolution was compromised as the image was captured through the thick protective viewing glass. Temporal resolution, image capture, and resolution were improved with the inclusion of cameras in the microscope column. With dedicated screens and video recording, time resolution of 0.03 s with atomic spatial resolution became achievable. Charge-coupled detector (CCD) cameras allowing digital acquisition along with image capture and processing subsequently resulted in significant improvements in collecting and handling data.Reference Alani and Pan101
Improving the fundamental temporal resolution limit requires replacing thermionic and field emission sources by photoemission ones.Reference Armstrong, Boyden, Browning, Campbell, Colvin, DeHope, Frank, Gibson, Hartemann, Kim, King, LaGrange, Pyke, Reed, Shuttlesworth, Stuart and Torralva102 For these sources, the temporal resolution is set by the duration of a short pulse of photo-excited electrons, which in turn is determined by the duration (10−3–10−15 s) of a laser pulse used to create the electron beam. The temporal resolution as well as the operating mode of a photoemission electron microscope is determined by the number of electrons in the beam. In the ultrafast TEM,Reference Flannigan, Lobastov and Zewail103–Reference Shorokhov and Zewail107 which has a temporal resolution in the range from femto- to pico-second, the electrons are confined such that the electron beam contains no more than ∼103 electrons. At the fastest timescales, typically the beam contains a single electron. As there is only a single electron in the beam, ∼108–109 shots are needed to form an image, limiting the types of sample stimulation that are amenable to study with this technique. However, the benefit is that there is no degradation in the spatial resolution of the microscope. In contrast, the electron beam in the dynamic TEM (DTEM) (milli- to nanosecond) is designed to contain sufficient electrons to obtain an image with a single shot.Reference Reed, Armstrong, Browning, Campbell, Evans, LaGrange and Masiel29, Reference LaGrange, Armstrong, Boyden, Brown, Campbell, Colvin, DeHope, Frank, Gibson, Hartemann, Kim, King, Pyke, Reed, Shirk, Shuttlesworth, Stuart, Torralva and Browning46, Reference Bostanjoglo and Otte108, Reference Bostanjoglo, Tornow and Tornow109 Typically, for a normal ∼10 μm field-of-view, this requires the pulse to contain 108–109 electrons. In this high current density beam, electron–electron interactions degrade the spatial resolution of the beam to between ∼5 and 10 nm, limiting the types of study that can be performed. However, the single shot approach means that the microscope can be used to study irreversible processes such as nucleation/growth and damage.Reference Reed, Armstrong, Browning, Campbell, Evans, LaGrange and Masiel29, Reference Ferreira, Robertson, Dehm and Saka33, Reference Campbell, LaGrange, King, Colvin, Ziegler, Browning, Kleinschmidt, Bostanjoglo, Howe, Laughlin, Lee, Dahmen and Soffa110–Reference Taheri, Reed, LaGrange and Browning112 With conventional sources the time resolution is tens of milliseconds and up with atomic resolution possible. This is the most common type of time-resolved TEM.Reference Saka113–Reference Sharma, Crozier and Treacy115
b. Methods of stimulating TEM specimens
A critical requirement for time-resolved microscopy is the ability to stimulate and excite the material so that the response can be captured in real time. The simplest method to stimulate a material is to use the electron beam itself. This approach was used initially to accelerate the build-up of contaminants on the sample surface; to induce the motion of dislocations in metalsReference Hirsch, Horne and Whelan116; to cause displacement damage, dislocation loops, and voidsReference Allen117–Reference Smith and Luzzi120; and to induce phase transformations.Reference Nagase and Umakoshi121–Reference Jencic, Bench, Robertson and Kirk124 Additional capabilities for stimulating the material require incorporating a mechanism within the limited volume available in the sample holder, modifying the microscope itself, or doing both. Specimen holders for heating, cooling, deforming, and indenting a material, as well as for applying magnetic or electric fields or exposing the sample to a gaseous or liquid environment, are all available commercially. In the time domain of tens of milliseconds, there are many examples on the use of these stages, and it is impossible within the scope of this brief review to do them justice. Select examples and references are given, and the interested reader is referred to collections of papers in special journal issues and conference proceedings.Reference Clark, Ferreira and Robertson32, Reference Butler125
As an illustration of the how these TEM stages have evolved, various devices available for probing mechanical properties of samples are shown in Fig. 8. Each method has advantages and disadvantages: the room temperature and high temperature stages, shown as Fig. 8(a), can probe deformation processes in any material that can be made electron transparent, but suffer from the inability to measure the applied load or the corresponding displacement and to control (or even to know) the sample temperature. Nevertheless, stages of this type have provided insight about dislocation sources, strengthening mechanisms, and dislocation–interface interactions.Reference Hattar, Han, Saif and Robertson50, Reference Dewald, Lee, Robertson and Birnbaum126–Reference Robertson, Ferreira, Dehm, Hull and Stach131 The simultaneous observation of deformation processes and acquisition of a macroscopic response measurement required new approaches, including, for example, integrated load and displacement transducers and gauges within a scaffold used to support a deposited electron transparent filmReference Haque and Saif49–Reference Espinosa, Zhu and Moldovan51; examples of such devices are shown in Fig. 8(b). These novel approaches require film deposition and microlithographic processing, and the devices are for single use. That is, as the device is an integral component of the TEM sample, it is destroyed during use. Finally, devices for indenting thin films or particles with micrometer to tens of nanometer dimensions have also been developed and used to great effect [Fig. 8(c)].Reference Espinosa, Zhu and Moldovan51, Reference Carlton and Ferreira132, Reference Deneen, Mook, Minor, Gerberich and Carter133

FIG. 8. Examples of TEM sample supports/holders that permit stimulation of samples, including (a) conventional schematic and actual stages that permit tensile loading, heating, or combinations thereof for disk-shaped specimens, (b) micro-electromechanical systems with integrated samples, and (c) stages for studies of indentation and compression. Based on Ref. Reference Robertson, Ferreira, Dehm, Hull and Stach131.
With appropriate confinement windows isolating the sample volume on a holder from the microscope vacuum, it is possible to expose a material to a liquid or a gaseous environment inside the electron microscope. The windows must not rupture under the pressure differential across them or be degraded by the liquid or gaseous environment. These requirements impact the material selected for the window as well as its thickness, which ultimately impacts the resolution that can be achieved. Nevertheless, such window-confinement holders have been used and have yielded new insights to catalytic reactions, particle growth, etc. For example, Ross and co-workers pioneered the use of such a device to study electro-deposition of copper on gold.Reference Radisic, Ross and Searson134, Reference Williamson, Tromp, Vereecken, Hull and Ross135 Using a liquid cell, they discovered that surface adsorption and diffusion controlled the early-stage kinetics of deposition, including cluster density and initial growth rate, while liquid diffusion limits behavior at longer times (see Fig. 9). Cluster nucleation was found to follow first-order kinetics, and 3D diffusion-limited growth explained the exponents of individual cluster growth.Reference Radisic, Vereecken, Hannon, Searson and Ross136 This work provided direct evidence to support the foundation of models of cluster nucleation and growth. Future developments for window-limited systems are in designing thinner but robust windows that can accommodate a wide variety of gaseous and liquid environments. Such advances will open new opportunities in areas of liquid–solid and gas–solid interactions as well as to biological systems.

FIG. 9. In-situ TEM observations of copper electrodeposited on a gold substrate. (a) The current transient during the early stages of growth, with four arrows denoting the times when the images in (b–e) were recorded. From Ref. Reference Radisic, Vereecken, Hannon, Searson and Ross136. Copyright ACS, reproduced with permission.
The alternate approach to including the stimulation mechanism in the sample holder is to modify the electron microscope itself. For example, gas cells have been incorporated inside the objective pole-piece, enabling gas pressures of a few tens of mega-Pascal of hydrogen gas with less than nanometer resolutionReference Lee, Dewald, Eades, Robertson and Birnbaum137, Reference Robertson and Teter138 or a few kilo-Pascal with atomic resolutionReference Boyes, Gai, Hanna, Sharma, Gai, Gajdardziska-Josifovska, Sinclair and Whitman139–Reference Gai, Sharma and Ross141; ion accelerators have been attached to microscope columns to enable the effects of bombarding materials with energetic particles to be investigated as a function of temperatureReference Allen, Funk, Ryan, Poker, Ila, Cheng, Harriott and Sigmon142–Reference Hinks144; metal sources have been incorporated for studies of the growth of thin films.Reference Drucker, Sharma, Weiss, Ramakrishna, Kouvetakis, Sharma, Gai, Gajdardziska-Josifovska, Sinclair and Whitman145, Reference Takeguchi, Wu, Tanaka and Furuya146 Recent developments in this area have seen modifications to instruments with correctors for spherical aberration for gas–solid interaction studies.Reference Gai and Boyes147
It is also possible to combine methods of stimulating the material, including, for example, simultaneous application of heat, stress, and atmosphere. For example, metals have been deformed at temperatures ranging from 77 to 1500 K in a gaseous environment to explore the fundamental processes controlling hydrogen embrittlement.Reference Robertson, Birnbaum, Sofronis, Hirth and Kubin148 An example of this effect is shown in Fig. 10. Figure 10(a) shows the stable arrangement of dislocations created by stressing the sample in vacuum and holding the load constant and allowing the dislocations to come to rest. Figures 10(b)–10(d) show changes in the dislocation arrangement when hydrogen gas is introduced into the cell (and concomitantly into the metal), Figs. 10(e)–10(f) show these dislocations stopping when the gas is removed, and Figs. 10(g)–10(l) show they move again when hydrogen gas is reintroduced. Two important features of this experiment were that the stage displacement was held constant during the introduction, removal, and reintroduction of the hydrogen gas and that this enhanced dislocation motion occurred in the presence of hydrogen gas only. The generality of these observations across several metals and alloys formed the basis for the hydrogen-enhanced localized plasticity mechanism of hydrogen embrittlement.Reference Robertson, Birnbaum, Sofronis, Hirth and Kubin148 Similarly, controlled-environment TEM has been used to gain an understanding on the function of catalysts and the structural and compositional modifications associated with loss of catalytic activity,Reference Gai, Sharma and Ross141, Reference Li, Liu, Nag and Crozier149, Reference Li, Liu, Nag and Crozier150 growth of nanotubes,Reference Gamalski, Moore, Treacy, Sharma and Rez151, Reference Sharma, Rez and Treacy152 etc.

FIG. 10. Series of in-situ TEM images of dislocations in iron under a constant applied load. In this series, frames (a–d) show that the dislocations move when hydrogen is introduced to the sample cell, frames (e and f) capture the cessation of motion when the gas is removed and frames (g–l) capture the motion when the gas is reintroduced. From Ref. Reference Robertson, Birnbaum, Sofronis, Hirth and Kubin148. Copyright Elsevier, reproduced with permission.
The DTEM approach to photoemission microscopy has been used to study a variety of processes such as martensitic phase transformations, crystallization, chemical reactions, and nanowire growth, and is currently being aimed towards biomolecular processes.Reference LaGrange, Armstrong, Boyden, Brown, Campbell, Colvin, DeHope, Frank, Gibson, Hartemann, Kim, King, Pyke, Reed, Shirk, Shuttlesworth, Stuart, Torralva and Browning46, Reference Bostanjoglo and Otte108–Reference Campbell, LaGrange, King, Colvin, Ziegler, Browning, Kleinschmidt, Bostanjoglo, Howe, Laughlin, Lee, Dahmen and Soffa110, Reference Taheri, Reed, LaGrange and Browning112, Reference Bostanjoglo and Thomsen-Schmidt153, Reference LaGrange, Campbell, Reed, Taheri, Pesavento, Kim and Browning154 For example, Lagrange et al. used the DTEM to discover the transient phases and morphological changes in the rapid solid-state chemical reaction occurring in reactive multilayer foils—self-propagating exothermic reactions initiated by an external stimulus.Reference LaGrange, Armstrong, Boyden, Brown, Campbell, Colvin, DeHope, Frank, Gibson, Hartemann, Kim, King, Pyke, Reed, Shirk, Shuttlesworth, Stuart, Torralva and Browning46Figure 11 shows a captured reaction front in a Al/Ni-7 wt% V multilayer. The reacted layer radiates outward from the point of impact of the laser—the marked change in contrast is readily distinguished by the line demarking reacted and unreacted material in Fig. 11(a). The cellular structure formed behind the propagation front is shown in Fig. 11(b). As this structure is metastable and disappears with time, its existence would be missed in conventional post-reaction studies. Such early results indicate the promise of the technique to capture and explore fast reaction processes.

FIG. 11. Snapshot capturing the rapid exothermic reaction between Ni-rich and Al-rich layers in a multilayer foil of Ni-Al-V in a DTEM. (a) Location where the reaction was triggered. (b) Reaction front captured during its travel. From Ref. Reference LaGrange, Campbell, Reed, Taheri, Pesavento, Kim and Browning154. Copyright Elsevier, reproduced with permission.
Ultrafast TEM has extremely high spatial and temporal resolution, but operates in the “pump-probe” mode, where a sample is repeatedly pumped with a specimen drive laser (which stimulates the material) and probed with the electron beam. Therefore, the technique provides a stroboscopic view of the material and is optimally suited to the study of perfectly reversible phenomena that can be stimulated by the laser pulse: for example, electronic phase changes, the observation of phonon modes, and picosecond changes in the electronic structure.Reference Chergui and Zewail28, Reference Flannigan, Lobastov and Zewail103–Reference Shorokhov and Zewail107, Reference Carbone, Barwick, Oh-Hoon, Hyun Soon, Baskin and Zewail155–Reference Yurtsever and Zewail159 An example of the latter application, which involves ultrafast EELS, is presented in Fig. 12, which shows the time–energy difference landscape of graphene as a function of time after a laser pulse. The primary change is the enhancement in the low energy regime, 7 eV, which is attributed to π plasmon resulting from interband ππ* transitions. An increase in the 27 eV bulk plasmon peak (π+σ) is also observed. Shown in Fig. 12(b) along with the changes in the EELS profiles is the temporal behavior of the c-axis; both compression and expansion along this axis is found. This reflects the anisotropic loading of the electronic states and the transfer of energy to strongly coupled phonons. As with the other time-resolved TEM approaches, the potential for these techniques has been established, and linking the methods with aberration correctors and in situ stages should open new areas for exploration.

FIG. 12. Ultrafast TEM data showing the change in the energy landscape of graphene during a laser pulse. (a) The time–energy difference landscape for times before and after the pulse (at t = 0). (b) Compression and expansion along the c-axis of the sample observed as time progresses. From Ref. Reference Carbone, Barwick, Oh-Hoon, Hyun Soon, Baskin and Zewail155. Copyright Elsevier, reproduced with permission.
c. Future prospects for time-resolved TEM
The primary area for development in time-resolved TEM is in the total functionality of stages or the sample scaffolds such that they are able to provide multiple forms of stimuli simultaneously along with the capability to measure the macroscopic property changes concurrently with the observation of the atomic processes. Examples of such devices that are emerging are the liquid and electrochemical cells and miniaturized mechanical property test frames briefly described earlier. These developments provide the opportunity to explore how structural and compositional evolutions occur and how they influence macroscopic material properties.
Extending the application of in situ stages and devices to aberration-corrected medium-voltage electron microscopes will provide new opportunities. For example, with chromatic aberration correction comes the ability to widen the pole-piece gap considerably, providing more volume in which to incorporate combined stimuli and measurement devices. This advance would also permit in situ observations on thicker samples—a key direction for future study of materials physics in light of the known effects of nearby surfaces on, for example, dislocation activity and point defect production in ion-irradiated materials.Reference Gilbert, Yao, Kirk, Jenkins and Dudarev160 For the ultrafast TEM, aberration correction could lead to sub-Ångström spatial resolution coupled with femtosecond temporal resolution and sub-100 meV energy resolution, revolutionizing many of the experiments that can be performed in the electron microscope. For the DTEM, aberration correction allows larger apertures to be used to form the images, reducing electron–electron interactions and leading to higher spatial resolution. A chromatic and spherical aberration–corrected system should allow atomic spatial resolution to be obtained for pulses that are ∼1–10 ns in duration, opening up many new areas of research.
While the range of accessible time scales spanned by current TEM techniques is already extremely wide, advances in the combined temporal and spatial resolution of DTEM and ultrafast TEM are anticipated. For example, radio frequency and ultra-cold atom sources offer the potential to increase the brightness and coherence of electron guns; more electrons can be contained in shorter pulse durations. Recent results have shown that ∼106 electrons can be included in a 30 fs pulse which, although not at the level required for single-shot imaging, foreshadows its achievement. Strategies for overcoming the detrimental electron–electron interactions in such pulses are also under consideration and may even permit access to sub-picosecond timescales coupled with nanometer spatial resolution in a single shot.Reference Reed, LaGrange, Shuttlesworth, Gibson, Campbell and Browning161 It thus seems that the resolution gap between ultrafast TEM and DTEM may one day be bridged by instrumentation advances.
B. Towards perfect-fidelity chemical mapping in the tomographic atom probe
APT enables the chemical distribution of a microstructure to be characterized in 3D, with near atomic-level resolution and a relatively large field-of-view. In this technique, specimens are prepared by fashioning small needles with a tip radius on the order of 100 nm. Atoms are removed sequentially from the tip of the needle-shaped specimen by a field ionization and field evaporation process, which can be accomplished by the application of either a voltage or laser pulse superimposed on a standing voltage.Reference Miller and Forbes162, Reference Kellogg and Tsong163 In either case, pulsed stimulation of the sample tip leads to a sequence of atomic removal; the specimen is deconstructed roughly one atom at a time. The identity of the emitted ions is determined in a wide-angle time-of-flight mass spectrometer equipped with a position-sensitive single atom detector.Reference Kelly and Miller30, Reference Miller31, Reference Miller and Forbes162 The atomic coordinates of the ions in the specimen are estimated from their impact position on the single atom detector and the order in which they were removed from the specimen.Reference Bas, Bostel, Deconihout and Blavette164, Reference Gault, de Geuser, Stephenson, Moody, Muddle and Ringer165 Based on the position of the ion detection and the time-of-flight measurement, it is possible to infer the chemical identity and original position in the sample of each detected atom. These data are subsequently reconstructed in the computer to provide a full 3D view of the atoms in the sampled volume.
The atom probe has evolved dramatically over the last few years, most notably in the accessible field-of-view. Early datasets comprised only 104–105 atoms, whereas present state-of-the-art instruments acquire datasets containing up to a billion atoms in the form of a truncated cone of up to 200 nm in diameter and typically between 100 and 500 nm in length. Such datasets may be interrogated in a variety of ways to extract information on the solute distribution at features such as clusters, precipitates, interfaces, dislocations, and internal surfaces.Reference Kelly and Miller30, Reference Miller31, Reference Miller and Forbes162Reference Miller and Reed166, Reference Tin, Yeh, Ofori, Reed, Babu and Miller167 The major improvements in instrumentation that have led to this dramatic advance are detailed in the following section along with some typical examples of the use of APT in materials science. The limitations to further advances are then laid out, along with the prospects for the next generation of APT instruments.
1. Advances in and applications of ATP
The watershed advances in APT described earlier have resulted from a number of complementary hardware and procedural improvements. The first of these was the introduction of the so-called local electrode, that is, a counter-electrode to the specimen positioned very close to the specimen tip; the local electrode typically has a central 25–50 μm aperture that is placed approximately the same distance from the apex of the specimen by a three-axis nanopositioning stage. The combination of size and specimen-to-aperture distance reduces the required voltage to produce a field evaporation event from the sample tip by about a factor of two. As a result, higher pulse rates may be used (up to 200 kHz), leading to acquisition times orders-of-magnitude shorter than in previous instruments. Additionally, with shorter times between pulses (at the standing voltage), there is less potential for unwanted preferential evaporation of the weakly bound atoms between pulses. Because of the very high rate of atom removal achievable with local electrodes, a related critical hardware development was a compatible single-atom detector based on crossed delay lines; such detectors enable the large field-of-view possible in modern APT experiments.
An example of a large and compelling dataset provided by a local electrode atom probe is shown in Fig. 13.Reference Tin, Yeh, Ofori, Reed, Babu and Miller167 This image shows a γ/γ′ nickel-based superalloy specimen, with γ′ particles segmented based on their composition. Note the large volume of the specimen, which spans half a micrometer along the needle axis, and which comprises 106 million atoms. Miller and Reed used this data to evaluate partitioning of a minority Re addition to the γ/γ’ interface.Reference Tin, Yeh, Ofori, Reed, Babu and Miller167

FIG. 13. Example of a large set of APT data, segmented to reveal the γ/γ′ structure of a nickel-based alloy. One hundred six million atoms were collected in this sample. The white surfaces are contours at 10 at.% Al concentration. From Ref. Reference Miller and Reed166. Copyright TMS. Reproduced with permission.
One of the main drawbacks of conventional APT, even with a local electrode, is the limitation of the technique to materials of sufficiently high electrical conductivity to support voltage pulsing; this requirement limits analysis essentially to metallic materials. To analyze semiconductors, ceramics, and even organic materials requires an alternate method of pulsing. As early as the 1970s, the feasibility of thermal pulsing to effect atom removal in the atom probe was demonstrated using a laser,Reference Kellogg and Tsong163, Reference Vurpillot, Houard, Vella and Deconihout168 but only with the introduction of stable and reliable solid-state lasers did this approach become viable for APT. Commercial laser-pulsed atom probes were introduced in 2005 and exhibit pulse durations (0.1–10 ps) and repetition rates (1 MHz) that easily exceed the needs of APT. In such instruments, the field evaporation is affected by the thermal excursion that is induced,Reference Vurpillot, Houard, Vella and Deconihout168, Reference Bunton, Olson, Lenz and Kelly169 which means that performance may be optimized by heating the smallest possible volume in the shortest possible time (so that cooling is rapid and the field evaporation time window is limited to ∼200 ps or less).
The most important outcome in the use of laser-assisted APT is that semiconductor and ceramic materials may now be routinely analyzed. For example, Inoue et al. used this method to analyze an entire field-effect transistor, comprising a gate, gate oxide, channel, source/drain extension, and halo. An example of an atom dot map is shown in Fig. 14.Reference Inoue, Yano, Nishida, Takamizawa, Tsunomura, Nagai and Hasegawa170 Inoue et al. were able to resolve the distribution of dopants within the transistor components, including As atoms in the source/drain extension and P atoms that preferentially decorated both the interface between gate and gate oxide and the grain boundaries in the polycrystalline Si gate itself. Others have used laser-assisted APT to examine bulk ceramic materials such as aluminaReference Stiller and Hattestrand171 and zirconia.Reference Chen, Ohkubo, Kodzuka, Morita and Hono172

FIG. 14. (a) 3D APT elemental map of source/drain region of a n-MOSFET and (b) cross-sectional TEM image. From Ref. Reference Inoue, Yano, Nishida, Takamizawa, Tsunomura, Nagai and Hasegawa170. Copyright Elsevier, reproduced with permission.
The final procedural adaptation that has significantly transformed the use of APT is the adoption of focused ion beam (FIB) sample preparation. Before the introduction of FIB, metallic needle-shape specimens were generally made by electropolishing. However, this method is not effective for most non-metallic specimens or site-specific locations. FIB machining enabled needle-shaped specimens to be fabricated from most forms of solid materials and also permitted specimens to be made from site-specific locations in a microstructure.Reference Miller, Russell, Thompson, Alvis and Larson173 In addition, the annular milling capability of a FIB permits final-stage processing of electropolished needles into a perfect cylindrical geometry; a circular cross section is critical to a high-fidelity reconstruction, ensuring uniform magnification over the surface.
2. Limitations and future prospects of ATP
APT is still far from achieving perfect-fidelity chemical mapping, correctly identifying 100% of the atoms in their exact locations within a specimen. To overcome existing barriers and to achieve this goal requires advances in two areas: ion detection with improved efficiency and mass resolution and reconstruction methods that account for trajectory aberrations. These issues are discussed in turn later.
Between issues of detection efficiency and mass resolution, the accuracy of APT for chemical concentration measurements stands to be significantly improved. For example, the current generation of crossed delay-line position-sensitive detectors detects only about 60% of the incident atoms. This is due to the use of microchannel plates (MCP) to amplify the signal from an individual ion into millions of electrons suitable for detection by the crossed delay-line detector. The other 40% of ions strike the intrachannel area of the MCP and are not amplified and, therefore, not detected. Unfortunately, for many problems in solute segregation and clustering, this efficiency is simply insufficient. For example, current APT datasets cannot yet be used to assess the degree of short- or long-range chemical order in a multicomponent crystal. Many other critical scientific questions, including, for example, the formation and arrangement of solute-centered clusters in binary glasses, nucleation of ordered phases, and interface segregation at low specific excess levels, also urgently require the development of 100% efficient single-atom detectors.
A related issue pertains to mass resolution. In wide field-of-view APT instruments, the mass resolution can be sufficiently improved by the incorporation of an energy-compensating lens, so that the mass peaks of all isotopes of all elements can be resolved to the noise floor. In voltage pulsed instruments, there is a small spread in the energy of the ions as they are field-evaporated from the specimen, leading to a loss in mass resolving power. Therefore, devices that compensate for this energy deficit, such as a magnetic sector, Poschenrieder, or reflectron lenses, are usually integrated into the mass spectrometer. The initial designs for such systems were based on a small acceptance angle instrument. Only very recently has a wide angle variant been proposed by Panayi, enabling both spatial and temporal focusing on the single atom detector.Reference Panayi174 This electrostatic lens improves the mass resolution and, more importantly, reduces the tails in the mass peak sufficiently that finely spaced mass peaks can be fully resolved to the noise floor. A disadvantage of the current generation lens is a reduction in the detection efficiency due to the use of a field-defining grid that blocks a few percent of the ions.
Even with 100% detection efficiency and improved mass resolution, issues of spatial resolution and aberrations in the reconstructed atomic coordinates remain significant barriers to perfect-fidelity APT. Although there are many materials for which the spatial resolution of APT for composition mapping in 3D is already unsurpassed, at present, APT data cannot be used to image the atomic lattice and to determine the orientation of a crystal. Improving spatial resolution, and removing aberrations in the reconstructed atomic coordinates, defines the future direction of development in ATP.
A distinction must be made between the spatial resolution in the longitudinal direction (analysis direction) and in the lateral directions. The former is determined principally by the visibility of atomic planes normal to the analysis direction, and the latter by fluctuations in the trajectories of atoms as they depart the tip. For a refractory metal at a low temperature, that is, tungsten at 50–60 K, the resolution of APT has been found to be about 0.15 nm in the lateral direction, and somewhat better at 0.06–0.14 nm in the longitudinal direction, based on Fourier analysis of the frequencies in an APT imageReference Vurpillot, Gruber, Duguay, Cadel and Deconihout175 and so-called spatial distribution maps.Reference Geiser, Kelly, Larson, Schneir and Roberts176 The greatest impediment to actually achieving such resolution in all materials and for all conditions is the presence of atom trajectory aberrations, which result from irregularity in the electrostatic fields that affect atom removal from the tip; although a perfectly smoothly curved tip would exhibit a uniform field and project ions uniformly upon the detector, irregularities of any kind in the structure of the tip surface lead to nonuniformity in the detected atom positions.
“Homophase aberrations” are those that arise from geometrical irregularities of the tip surface. Faceting occurs in crystalline materials when atoms evaporate preferentially from the edges of close-packed planes and not from the plane interior regions. Because a facetted tip is not smoothly curved, ions are preferentially displaced away from the center of the facet, leading to a perceived higher atomic density along facets. Figure 15 shows a histogram of detected atoms from a tip of aluminum, illustrating this effect. Aberrations of this type can be as large as 2 nm or more at the center of major poles in materials with pronounced faceting; in such materials, resolution is thus position-dependent, with the best spatial resolution occurring between the facet edges. Similar effects are observed in single-phase polycrystals, where grain boundaries can exhibit either a higher or a lower density of atoms compared to the grain interior.Reference Miller, Kenik and Zagula177, Reference Detor, Miller and Schuh178

FIG. 15. Field evaporation histogram of events hitting the detector for an aluminum atom probe tomography (ATP) specimen. This figure illustrates homophase aberrations that occur in some materials and which are very pronounced in aluminum. The darker blue regions receive fewer ions and indicate regions on the tip apex that have facets. Image courtesy of T.F. Kelly.Reference Kelly and Miller30
“Heterophase aberrations” occur because different materials require different electric fields to evaporate atoms.Reference Miller, Cerezo, Hetherington and Smith179 When two phases with different evaporation fields are present on the surface of an APT specimen, the tip shape adapts as illustrated in Fig. 16(a) and the projection magnification thus varies across the image. The global resolution in APT of heterogeneous materials thus varies from barely affected (when the two or more evaporation fields are almost identical) to severely distorted (when the two or more evaporation fields are very different).

FIG. 16. Schematic illustration of the origins of heterophase aberrations caused by different evaporation fields, E, in the matrix E 0 and the second phase, E β.
The simple reconstruction algorithm in widest use today is based on the assumption of a smoothly curved tip. Aberrations of the kind described earlier are endemic to the wide field-of-view of state-of-the-art instruments, which can virtually never be expected to achieve uniform evaporation. To some extent, improved handling and filtering of APT data may partially mitigate some of these issues in specific cases. For example, Moody et al. have removed regions of known aberration from APT images and have shown significant improvements in the visibility of atomic planes as a result.Reference Moody, Gault, Stephenson, Haley and Ringer180 In the general case, though, what is required is an improved integration of tip structure effects on atomic trajectories into the reconstruction process. When this topic has been modeled, the step of reliably incorporating tip shape into the reconstruction procedure is nontrivial. It requires, first of all, that the tip shape be known at a given time. Conceivably, a good model could then predict the order in which atoms would be removed, as well as their specific trajectories, and so reconstruction could be conducted knowing only the tip shape at the outset of the experiment. Alternatively, the tip shape could be periodically assessed and used to correct the model in situ. In any event, knowledge of the tip shape will almost certainly require an independent measurement, suggesting the possibility of, for example, integrating APT with electron tomography.Reference Miller and Kelly181
An alternative approach is to visually observe the atomic structure before and after each and every atomic removal event. Again, this might be possible by synergizing APT with another method of imaging. For example, Miller et al. viewed a NiZr intermetallic atom probe tip with an imaging gas (in field ion microscope mode) before field evaporating a single atom; they then cycled this procedure to watch the sequence of atom removal.Reference Miller31Reference Miller, Cerezo, Hetherington and Smith179 A series of field ion micrographs showing eight successive atom removals from this tip is shown in Fig. 17. It is at least conceivable that such a strategy could be scaled to larger samples and millions of atoms, providing a direct view of the state of the tip and perhaps even the specific atoms being removed at any given time; the engineering challenge to make this a routine procedure with high acquisition rates, however, is daunting.

FIG. 17. Series of field-ion micrographs showing one region on a Ni-Zr intermetallic atom probe tip. Between each successive image in the sequence, a single atom was field-evaporated from the tip. After Ref. Reference Miller, Cerezo, Hetherington and Smith179. Reproduced by permission of Oxford University Press.
A final limitation of APT is that the technique is inherently a static one; because of its destructive nature, it is not possible to even conceive of in situ microstructural observations with APT (i.e., barring the development of a revolutionary new ability to alternately disassemble and reassemble the same structure). At best, time dependency of material processes can be explored through a sequence of “snapshots” acquired from different samples treated for different times.
C. Towards 4D characterization with x-rays and neutrons
X-rays and neutrons have long been reliable workhorses for the characterization of material structure, with the largest applications being in radiographic imaging of microstructure and determination of crystal structure and orientation. These classical techniques can be extended to reveal the same information, but with a full 3D view, and the past decade has seen such 3D experiments become routine. At the same time, synchrotron x-ray sources permit a substantial increase in the volume of bulk specimens that can be probed, and neutron user facilities offer complementary capabilities with even greater penetration distances. Owing to the nondestructive nature of these techniques, time-resolved experiments are also possible, giving access to the full 4D space in bulk specimens. This section reviews recent applications of x-ray and neutron beams, highlighting the state-of-the-art of these capabilities and describing the future prospects for each technique.
1. X-ray tomography: Advances and applications
Tomography is probably the most well-known 3D x-ray imaging method and basically consists of recording a series of many radiographs of the same sample viewed at different angles. If different components of the microstructure have sufficiently different absorption coefficients, a 3D image of the microstructure can be reconstructed using algorithms similar to those mentioned for electron tomography.
For relatively smaller and/or lower density specimens, x-ray tomography (XRT) can be carried out with lower-energy beams available on desktop instruments. And, indeed, commercial XRT instruments, with a characteristic resolution generally of some tens of micrometers, have proliferated rapidly in recent years. An example of a two-phase structure that has been characterized extensively by XRT is snow firn, multilayer snow present on the top 70–100 m of polar ice sheets, which is composed of air and water ice. XRT has been used to visualize the structure of the ice within the firn, as shown in Fig. 18.Reference Freitag, Kipfstuhl and Faria182 One of the key benefits of this technique is its nondestructive nature, which permits extensive subsequent examination of the same samples of firn using other techniques.Reference Cullen and Baker183–Reference Obbard, Baker and Sieg191

FIG. 18. Example of output data from computed x-ray tomography (XRT) using a benchtop instrument. This image is a 3D reconstruction of firn (snow ice with porosity) taken from the Antarctic. The sample volume is 8 mm on each side. A reconstructed firn cube of 16 mm (400 voxels) side length from 8 m depth. The ice phase is displayed in black; pores are transparent. From Ref. Reference Freitag, Kipfstuhl and Faria182. Reprinted from the Annals of Glaciology with permission of the International Glaciological Society.
When carried out on a synchrotron beamline, the capabilities of XRT are enhanced in the size of the sample that can be probed, as well as in the resolution, which approaches the micron range for a conventional set up. An example of this is shown in Fig. 19, which shows a directionally freeze-cast titanium foam. This material was produced from a solidified mixture of ice and Ti powder, from which the ice was removed by sublimation before sintering of the powder.Reference Chino and Dunand192, Reference Deville193 The resulting titanium foam has application in bone replacement, as it exhibits the same aligned, elongated pore architecture.Reference Spoerke, Murray, Li, Brinson, Dunand and Stupp194 The architecture of this foam was studied by XRT performed at the Advanced Photon Source at Argonne National Laboratory with a 45 keV synchrotron x-ray beam with 6 μm/pixel resolutionReference Fife, Li, Dunand and Voorhees195; note the improvement in resolution as compared with the results from Fig. 18 using a desktop instrument.

FIG. 19. Example of XRT data collected at a synchrotron source, showing the structure of directionally freeze-cast titanium foams, showing pores as solid and metal as empty; the gradient direction is along the z axis. The inset shows an optical micrograph taken along the z-axis. From Ref. Reference Chino and Dunand192. Copyright Elsevier, reproduced with permission.
Although reconstructed 3D images are visually compelling and can offer some insight merely by inspection, the greatest benefit of XRT is realized when the data are subsequently plied to a quantitative purpose. As the field evolves, greater emphasis is being placed on detailed quantification of microstructure, beyond the scalar metrics accessible by, for example, stereology on plane sections. For example, the 3D pore connectivity and internal surface area can be measured.Reference Freitag, Wilhelms and Kipfstuhl196–Reference Lomonaco, Chen and Baker198 These quantitative structural details are of great importance in interpreting the climatic record because the sintering of ice and entrapment of air in closed pores are key time signatures used to date various locations in ice cores.Reference Schwander, Sowers, Barnola, Blunier, Fuchs and Malaize199–Reference Bender, Sowers and Lipenkov202 In the case of the titanium foam (Fig. 19),Reference Chino and Dunand192 the surface topology was explored in terms of the curvature distribution function and compared with the same distribution from trabecular bone, of which it is an intended simulacrum. A similar analysis can be conducted with the distribution of surface normal vectors, which speaks directly to anisotropy and directionality of the structure. Such 3D microstructure metrics are much more powerful than simple scalar values such as volume fraction, surface area, average feature size, and connectivity and, hopefully, will be used more frequently in the future to analyze XRT data.
In recent years, there have been some significant advances in improving the resolution of synchrotron-based XRT. For example, the increasing precision of nanofabricated Fresnel lenses has progressively refined the focus of x-ray beams to the point where ∼20 nm features may be imaged. An example of using such high-resolution XRT is shown in Fig. 20, which shows results from a study of coarsening in gold foams.Reference Chen, Chu, JaeMock, McNulty, Qun, Voorhees and Dunand203 Data such as these offer much more than simply a visualization of a static structure, as the ability to perform nondestructive imaging of the same volume after, for example, thermal exposure permits time-resolved studies of structure evolution to be undertaken. Quantitative analysis of the 3D dataset can lead to a detailed understanding of mechanisms of structure change. In the example from Fig. 20, Dunand et al. were able to conclude that the de-alloyed nanoporous gold structure is not produced by a coarsening process dominated by bulk diffusion, but rather exhibited quantitative characteristics closer to a phase-separated system.Reference Chen, Chu, JaeMock, McNulty, Qun, Voorhees and Dunand203

FIG. 20. (a) SEM image of nanoporous gold annealed at 500 °C for 30 min to coarsen pore size; (b) a tomographic reconstruction of nanoporous gold annealed at 400 °C for 30 min (imaging with transmission x-ray microscopy at the Advanced Photon Source, beamline 32-ID-C); (c) a small volume taken from (b), showing the detailed interconnected structure and (d) highlighting the zero mean curvature region, which forms a continuous network among the surface. From Ref. Reference Chen, Chu, JaeMock, McNulty, Qun, Voorhees and Dunand203. Copyright Elsevier, reproduced with permission.
2. 3D x-ray diffraction and the mapping of crystallographic orientations
Although XRT is useful for the visualization of phase domains based on transmitted intensity, methods that provide spatial resolution and contrast based on crystal orientation or other diffraction-based data are of increasing interest. The method called “3D x-ray diffraction” (3D-XRD) is a synchrotron x-ray technique developed over the past decade. The instrument is an x-ray microscope that non-destructively characterizes bulk microstructure and simultaneously gives complete crystallographic orientation information. Often, the speed of the instrument is sufficient to follow processes of microstructural evolution in situ while the bulk samples are exposed to external stimuli.
Full details on the theory behind and evolution of the 3D-XRD apparatus are available in a monograph by Poulsen,Reference Poulsen17 but the main operational principal is the use of two sets of detectors that are used for two different types of measurements, as shown in Fig. 21. Far-field detectors with relatively large pixel sizes (e.g., ∼200 μm) are placed far from the sample for characterization of grain sizes, orientations, and strains, while detectors with small pixel sizes (typically ∼1 μm) are placed very near the sample for optimal spatial resolution and full mapping of microstructures. As with other synchrotron-based methods, the large working volume available permits the use of furnaces, cryostats, or mechanical test rigs.

FIG. 21. The 3D-XRD set-up. A monochromatic high energy x-ray beam is incident on the sample. Two sets of detectors are used: Near-field detectors at position L1 and L2, which are typically 2–10 mm from the sample for full mapping of microstructures, and a far-field detector typically 40 cm from the sample for fast characterizations of sizes, orientations, and strains. Based on Ref. Reference Poulsen17.
3D-XRD measurements are typically carried out with x-ray energies in the range of 45–100 keV, and include characterization of position and volume, 3D shape, crystallographic orientation, and elastic and plastic strain of individual microstructural elements such as grains and particles,Reference Poulsen17, Reference Larson, El-Azab, Yang, Tischler, Liu and Ice204–Reference Larson, Yang, Tischler, Ice, Budai, Liu and Weiland207 strain within dislocation cells,Reference Budai, Liu, Tischler, Pan, Norton, Larson, Yang and Ice208 and beneath nanoindentations.Reference Yang, Larson, Pharr, Ice, Budai, Tischler and Liu209 The spatial resolution at present state-of-the-art facilities is about 5 × 5 × 1 μm3, while microstructural elements down to about 50 nm can be detected, provided overlap of diffraction spots on the detector can be avoided.Reference Poulsen17 The temporal resolution can be on the order of seconds to minutes for measurements using the far-field detector only, whereas full mapping experiments using the near-field detectors typically require on the order of a few hours. In addition to the standard 3D-XRD setup depicted in Fig. 21, there are other instruments using somewhat different measuring strategies that are deployed at, for example, Argonne National Laboratory and Hasylab.Reference Ice and Larson18, Reference Liu, Ice, Larson, Yang, Tischler and Budai19, Reference Bunge, Wcislak, Klein, Garbe and Schneider210 These offer different combinations of resolutions; for example improved spatial and orientational resolution but poorer temporal resolution due to longer exposure/scan times.
One example of the use of 3D-XRD has been to resolve the nucleation and growth of individual recrystallization nuclei.Reference Schmidt, Nielsen, Gundlach, Margulies, Huang and Jensen211 The growth of individual nuclei through the deformed matrix of a cold-rolled single Al crystal was followed in situ during annealing, with a time resolution of 10–20 min; a series of snapshots from this experiment is shown in Fig. 22. As the deformed matrix in which these nuclei were growing was very homogeneous with interior misorientations below 7°, it was expected that the nucleus would grow homogeneously in space and time. This was not observed experimentally; on the contrary, all nuclei evolved with quite irregular shapes, typically growing faster along the rolling direction. What is more, local protrusions were very often seen to form on the moving boundary; small segments would locally move very quickly, with the neighboring boundary segments following at a slower rate to eliminate grain boundary protrusions and intrusions. These local 3D results have spurred vigorous modeling efforts.Reference Godiksen, Trautt, Upmanyu, Schiotz, Jensen and Schmidt212–Reference Sreekala and Haataja214 Whereas interrupted start-and-stop–type motion has also been seen in in situ SEMReference Zhang, Godfrey, Liu, Liu and Jensen215, Reference Anselmino216 and TEMReference Kacher, Robertson, Nowell, Knapp and Hattar217 studies of grain growth, the bulk observational capability of 3D-XRD established this as a real behavior and not one dominated by surface/thin film effects.

FIG. 22. Time series of images showing the growth of a nucleus during recrystallization of deformed aluminum. These images show the nonuniform growth rate of the grain (c), and the development and advancement of protrusions from different parts of the grain at different times (e and h). From Ref. Reference Schmidt, Nielsen, Gundlach, Margulies, Huang and Jensen211. Copyright AAAS, reproduced with permission.
3. Neutron-based characterization in 4D
Neutron scattering is a powerful probe for characterizing the structure of materials at multiple length scales, owing to some unique properties of neutrons. First, they are highly penetrating, permitting measurements on bulk specimens rather than from surface regions or thin samples. Second, unlike x-ray scattering where the scattering factor scales with atomic number, the neutron scattering length varies sporadically with atomic number and also from one isotope to the next. For example, neutrons are scattered strongly by light elements such as H or O. As a result, neutrons have been used to determine the position of some chemical species that could not be determined otherwise. Finally, neutrons tend to have wavelengths in the range of Ångströms, and as a result can be used to probe structure at scales ranging from the atomic to sub-micron level. For example, diffraction studies provide insight on atomic/crystal structure, while small-angle scattering studies probe length scales extending up to hundreds of nanometers and play an important role in studies of, for example, coarsening in Ni-based superalloys,Reference Bruno, Pinto and Reimers218 nanoscale clustering in metallic glasses,Reference Ma, Stoica, Wang, Lu, Xu and Kramer219 or oxide-dispersion-strengthened alloys.Reference Ratti, Leuvrey, Mathon and de Carlan220 At even larger length scales, neutrons can be used for radiography and tomography in the same fashion as are electrons and x-rays.
One of the most valuable and widely adopted uses of 3D neutron analysis is the mapping of residual stresses in bulk components. Based on the geometry of the incident beam and the diffraction spots, it is possible to identify the diffraction signal from specific locations within a bulk sample and by extension to develop a 3D map of the diffraction signal and any information that it contains, including lattice strains (from which stresses are inferred). The basic approach is described in more detail in Refs. Reference Noyan and Cohen221–Reference Wang223 and successful examples include stress mapping in engineering components including welds,Reference Bouchard, Withers, McDonald and Heenan224–Reference Wang, Payzanta, Taljata, Hubbarda, Keisera and Jirinecb226 rail heads,Reference Webster, Wang, Mills and Webster227 aircraft wings,228 boiler tubes used in paper mills,Reference Wang, Payzanta, Taljata, Hubbarda, Keisera and Jirinecb226 and natural gas cylinders.Reference Wang, Payzanta, Taljata, Hubbarda, Keisera and Jirinecb226 The measurement techniques have advanced to a stage where, in many cases, the experimental data can be quantitatively compared with predictions by finite element calculations,Reference Wang, Payzanta, Taljata, Hubbarda, Keisera and Jirinecb226, Reference Feng, Wang, Spooner, Goodwin, Masiasz, Hubbard and Zacharia229 thereby providing guidance on the design and life prediction of structural components.
A significant puzzle in early neutron analyses of residual stress was how to interpret results obtained from multiple planes. The significance of intergranular strains in polycrystalline materials was recognized here. Lattice strains are linear in the elastic range, while they are nonlinear when plastic deformation occurs. The additional elastic strain that develops in the grains to accommodate inhomogeneous plastic deformation during the macroscopic elasto-plastic transition is termed intergranular or type II strain. Signature intergranular strains develop due to the activation of select slip planes, for example. For this reason, intergranular strains have been used as a fingerprint to gain insight to elastic and plastic anisotropy in polycrystalline metals. For example, by measuring the intergranular strains and using polycrystal plasticity modeling to interpret the results, Wollmershauser et al. demonstrated that the intergranular strain evolution of CeAg is nearly identical to that of NiAl, indicating that they share a common primary plastic deformation mechanism, that is, <100>{011} ‘‘cube” slip.Reference Miller and Reed166, Reference Wollmershauser, Kabra and Agnew230 As another example, a recent study on nanocrystalline Ni revealed no intergranular strains, providing evidence of grain-boundary–mediated plasticity.Reference Cheng, Stoica, Wang, Ren, Almer, Horton, Liu, Clausen, Brown, Liaw and Zuo231, Reference Fan, Li, Bin, Choo, Liaw, Saleh, Clausen and Brown232
Significant intergranular strains also develop as a result of cyclic loading. This was demonstrated by Wang et al. for 316 stainless steel.Reference Wang, Tian, Stoica, Wang, Liaw and Richardson233Fig. 23 shows the experimentally determined intergranular strains as a function of the tilt angle relative to the loading direction as a function of the number of cycles. The differences in the orientation dependences are due to the presence of intergranular stresses. Such data provide a more rigorous test for numerical modeling of deformation behavior in polycrystalline materials. In some materials, cyclic loading leads to a phase transformation. For example, under cyclic loading, ULTIMET, a Co-based ferritic alloy transforms from retained austenite to the more stable hcp phase.Reference Benson, Liaw, Saleh, Choo, Brown, Daymond, Huang, Wang, Stoica, Buchanan and Klarstrom234, Reference Benson, Stoica, Liaw, Choo, Saleh, Wang, Brown and Klarstrom235 In situ neutron diffraction showed that the volume fraction of the hcp phase increases with increasing number of load cycles.

FIG. 23. Lattice strain distributions in 316 stainless steel obtained with 111, 200, and 220 reflections as a function of tilt angle relative to the loading direction at different number of fatigue cycles. From Ref. Reference Wang, Tian, Stoica, Wang, Liaw and Richardson233. Copyright Nature Publishing Group, reproduced with permission.
4. Future prospects for x-ray and neutron analysis in 4D
Major trends for advances in the tomography techniques include the introduction of new sources of contrast for tomographic imaging. For example, phase contrast or XRD contrast tomography could provide not only a spatial reconstruction of phase domain shapes but also simultaneous mapping of crystal orientations.Reference Ludwig, Schmidt, Lauridsen and Poulsen236, Reference Johnson, King, Honnicke, Marrow and Ludwig237 Of course, spatial resolution is always improving, with values in the range of ∼10 nm becoming possible due to improved optics. Temporal resolution remains a key issue for these techniques, with acquisition times below 30 min being highly desirable for in situ studies of structure evolution. Thus, a key development would be higher brightness sources that would allow experiments to be performed in real time; for example, the incorporation of rotating anode x-ray sources into laboratory-scale XRT experiments could provide more than an order of magnitude increase in brightness and a corresponding decrease in exposure time. Free-electron x-ray lasers may also lead to dramatically reduced exposure times for XRT experiments.
Similarly, 3D-XRD may be expected to advance in terms of spatial and temporal resolution; the integration of new detector architectures, such as arrayed or structured scintillators, rather than CCD cameras, could dramatically improve resolution. Perhaps more important is the movement toward standardization of analysis software for 3D-XRD data. In the future, standardized data acquired at public beamlines perhaps could be made openly available as a service to the community. Another key direction for the advancement of 3D-XRD is to combine it with various tomographic methodologies. There are already published examples of such data,Reference King, Johnson, Engelberg, Ludwig and Marrow7 and the resulting synergies may be expected to become more commonplace through fully integrated parallel experiments in the coming years. Similarly, the ability of 3D-XRD to map local strains tomographically within a composite material has been demonstrated, but has yet to find wide application.Reference Nielsen, Poulsen, Beckmann, Thorning and Wert238
For neutron analysis, new facilities and instrumentation upgrades promise major advances in the coming years. For example, the Spallation Neutron Source at Oak Ridge National Laboratory houses several instruments specifically designed for structural studies, including POWGEN, the high resolution powder diffractometer; VULCAN,Reference Wang, Holden, Rennich, Stoica, Liaw, Choo and Hubbard239, Reference Wang, Holden, Stoica, An, Skorpenske, Jones, Rennich and Iverson240 the engineering diffractometer; NOMAD, nanoscale ordered materials diffractometer; extended Q-range small-angle neutron scattering; and VENUS for neutron imaging.Reference Mason, Abernathy, Anderson, Ankner, Egami, Ehlers, Ekkebus, Granroth, Hagen, Herwig, Hodges, Hoffmann, Horak, Horton, Klose, Larese, Mesecar, Myles, Neuefein, Ohl, Tulk, Wang and Zhao241 The VULCAN diffractometer, in particular, is designed for the materials science and engineering community, with a focus on mechanical behavior. This instrument offers a time resolution of 1 s or less and can accommodate samples in a controlled atmosphere, under mechanical loads, and at temperatures up to 1600 °C. For the now widely accepted method of neutron measurement of residual stresses, the rapid acquisition time of such new instruments promises a resolved view of stress evolution during, for example, processing or cyclic loading. Already there have been several attempts to determine the stress and temperature evolution during welding with neutron scattering, including, for example, during friction stir welding.Reference Woo, Feng, Hubbard, David, Wang, Clausen and Ungar242 With a stroboscopic measurement technique, it should be possible to determine how the intergranular strains change within a load cycle or under complex loading states.
D. Mesoscale characterization in 3D
A well-established method for conducting 3D spatial characterization at the mesoscale is by serial sectioning, which is a conceptually simple strategy consisting of two principal steps. The first step is to create a planar surface through careful removal of a known volume of material. After sectioning, the newly exposed surface is analyzed using a variety of 2D characterization methodologies such as standard optical or electron imaging methods, or those that provide maps of the local crystallographic or compositional information. The combined task of sectioning and imaging is repeated until the desired material volume is interrogated. After data acquisition is complete, a 3D volume is reconstructed from the stack of 2D images.
1. Advances in and applications of serial sectioning
Serial sectioning studies have a long history of comprising labor-intensive cycles of polish-and-image. Most studies up to the turn of the century involved optical imaging to acquire images most rapidly,Reference De Graef, Kral and Hillert243 with only rare and monumental efforts at more complex imaging (i.e., high-resolution SEM,Reference Lund and Voorhees1, Reference Lundy, Edens and Brown197, Reference Mangan, Lauren and Shiflet244 building montages to achieve a larger field of view,Reference Tewari, Gokhale and German245 or orientation imagingReference Saylor, El-Dasher, Sano and Rohrer246–Reference Wall, Schwartz and Nguyen253). Perhaps the finest-resolution serial-sectioning dataset collected by manual polishing and imaging is shown in Fig. 24, from the work of Lund and Voorhees on a γ/γ′ nickel-based superalloy.Reference Lund and Voorhees1 Steps toward automation of serial sectioning are occurring, and the increasing sophistication of computer controls and robotics promise further advances.Reference Alkemper and Voorhees11, Reference Spowart, Mullens and Puchala254

FIG. 24. Characteristic portion of the 3D-rendered microstructure showing the γ′ precipitates in a γ/γ′ nickel-based superalloy. Dimensions are 7.5 × 7.5 × 3.6 (10−6 m3). From Ref. Reference Lund and Voorhees1. Copyright Taylor and Francis Group, reproduced with permission.
By far, the most significant advance for serial sectioning analysis was the introduction of the FIB and combined FIB–SEM instruments over the past decade. These microscopes are capable of focusing energetic ions (typically 30 kV Ga+) to spot sizes on the order of 5–20 nm. Rastered movement of the ion beam enables the controlled removal of material at the nanoscale via ion sputtering interactions, which for a serial sectioning experiment can be used to control the section thickness to a value of 10–15 nm using closed-loop control measures, although larger section values are typically used. By comparison, mechanical polishing has been used to achieve section thicknesses only as fine as about 100 nm. In addition to this unrivaled sectioning capability, FIB microscopes have other advantages. First, ion milling is a fairly universal method for micromachining, and suitable surfaces have been successfully prepared in metals, ceramics, polymers, and electronic and biological materials. Second, the method results in relatively low damage as compared with typical abrasive or cutting methods, which helps preserve the microstructural features, especially for multiphase materials that contain both soft and hard phases or those that contain significant porosity. However, the ion beam can introduce damage or artifacts. For example, Konrad and co-workers analyzed the microstructure around a Laves phase in an iron-aluminide intermetallic alloy and found that, although 30 kV ion beam sectioning provided a surface suitable for EBSD analysis of the Fe3Al matrix, the crystal structure of a Laves phase particle could not be obtained because of ion-induced surface damage.Reference Konrad, Zaefferer and Raabe255 More recent efforts to characterize the effect of the ion accelerating voltage on the quality of EBSD patterns suggests that future serial sectioning experiments should incorporate low-kilo-voltage milling protocols to minimize this issue.Reference Michael and Giannuzzi256
The selection of the in-plane imaging resolution and serial section thickness (spacing between consecutive sections) should be considered before performing the experiment. A rough guideline for selecting the serial sectioning thickness is to ensure that the feature or average-feature-of-interest will be observed in at least 10 sections, and the in-plane resolution is typically on the order of or smaller than the serial sectioning thickness. It is also important for nanoscale FIB–SEM tomography studies to consider the information limit for the characterization methodology that is to be used to ensure that the voxel dimensions are at least equal to or greater than this value to avoid collecting “empty magnification.”
Recent examples showcasing the value of automated serial sectioning are the works of Wilson et al.Reference Wilson, Kobsiriphat, Mendoza, Chen, Hiller, Miller, Thornton, Voorhees, Adler and Barnett257 and Gostovic et al.,Reference Gostovic, Smith, Kundinger, Jones and Wachsman258 who used FIB–SEM serial sectioning to study the active cathode regions of conventional solid-oxide fuel cells. Comprising three phases (La0.8Sr0.2MnO3 or LSM, yttria stabilized ZrO2 or YSZ, and pores), the functionality of the cathode in reducing oxygen is directly related to the total length of phase triple boundary per unit volume. In addition, all three phases must percolate to facilitate the necessary transport processes. Connectivity and percolation represent key property-controlling topology information that is very difficult or even impossible to infer from 2D views. As an example of this, the 3D reconstruction of Wilson et al. revealed that a fraction of the triple phase boundaries were not interconnected and, therefore, could not contribute to the electrochemical processes in the cell.Reference Wilson, Kobsiriphat, Mendoza, Chen, Hiller, Miller, Thornton, Voorhees, Adler and Barnett257 Gostovic et al. related the electrochemical properties of the cathode to the porosity, triple phase boundary length, and tortuosity.Reference Gostovic, Smith, Kundinger, Jones and Wachsman258
The electron beam in a dual-beam FIB instrument can be used for more than imaging, which permits FIB serial-sectioning studies with far richer datasets. For example, spectroscopy can provide mapped compositional information and EBSD can provide local information on the crystallographic character of bulk crystalline or polycrystalline material.Reference Adams, Wright and Kunze259–Reference Zaefferer, Wright and Raabe261 In fact, the combination of EBSD with FIB serial sectioning is arguably one of the most important advances in structural characterization at the super-grain scale. EBSD provides high spatial resolution (approaching 10 nm), reasonable angular resolution (as good as ∼0.5°), ease of adaptation to virtually any electron beam instrument, and automated data collection and mapping capability. These patterns provide information on the crystal structure, crystallite lattice orientation, and a measure of crystallite integrity (lack of defect content), leading to insight about texture, phase morphology, elastic strain, strain localization, and grain boundary structure.
One significant advantage of collecting crystallographic or chemical maps compared to collecting only image data is the classification of the data into physically-meaningful objects (e.g., grains, phases), which can be performed using automated software routines, as compared to image-based data classification that often requires significant human supervision. The commercial manufacturers that supply EBSD instrumentation have developed robust segmentation and analysis methods to convert the Kikuchi band pattern into a crystallographic orientation. Thus, the “difficult” part of image segmentation has already been solved, and more importantly, the singular characteristic that defines a grain—common crystallographic orientation—is an inherent part of the data collected during the experiment. The studies of GroeberReference Groeber, Haley, Uchic, Dimiduk and Ghosh10, Reference Groeber, Ghosh, Uchic and Dimiduk262 and Zaefferer and coworkersReference Konrad, Zaefferer and Raabe255, Reference Zaefferer, Wright and Raabe263 have demonstrated that grain structures can be readily defined using this methodology. Similar comments hold as well for elemental image data, especially when used in conjunction with multivariate statistical analysis software.Reference Kotula, Keenan and Michael264
One of the principal drawbacks of present 3D FIB–SEM analysis that incorporates crystallographic or chemical mapping is the relatively slow rate of data acquisition. For example, although the acquisition rate for EBSD has increased significantly since the first commercial systems appeared in the early 1990s when the data collection rate was about 1 pattern per second, the fastest commercial systems can obtain and analyze only above few hundred patterns per second under ideal conditions. The total time required to collect an EBSD map is often practically selected to be on the order of a few minutes to over an hour for each section, and when combined with milling steps that extend from minutes to hours, the cumulative time per serial section can approach several hours. A case in point is the state-of-the-art serial sectioning experiment in 2006 (cubic voxel size of 0.25 μm and an analysis volume of 96 × 46 × 36 μm3) that produced a data cube with over 10 million EBSD data points and required over 148 h to collect.Reference Groeber, Ghosh, Uchic and Dimiduk262
The emphasis herein has been on 3D spatial analysis, although time resolved studies are possible. It has been used to investigate recrystallization,Reference Humphreys265 grain growth,Reference Rofman, Bate, Brough and Humphreys266, Reference Tsurekawa, Fukino and Matsuzaki267 grain boundary migration,Reference Taheri, Sebastian, Reed, Seidman and Rollett268 phase transformation,Reference Seward, Celotto, Prior, Wheeler and Pond269 and deformation processes,Reference Huang, Humphreys and Brough270–Reference Niederberger, Mook, Maeder and Michler272 with a time resolution determined by the scan rate, which can be on the order of tens of seconds depending on the area being scanned and the resolution. Improvements in this area are likely to involve data acquisition as well as data manipulation.
2. Prospects for future advances in serial sectioning studies
Serial sectioning experiments provide a near-term and direct pathway for collecting 3D data from the micro- to macroscale. For serial sectioning experiments of macroscale volumes, current automated instrumentation allows one to readily acquire image data via optical microscopy and mechanical removal methods, but incorporation of crystallographic or chemical information requires manual intervention. At the microscale, there is a greater quantity of spectral information that can be included in FIB–SEM data collection processes via either electron or ion imaging and their derivatives or chemical or crystallographic mapping.
While the software to analyze 2D orientation data is rather advanced and available commercially, that for 3D data sets is still in its infancy, and there are many outstanding issues to be resolved in proper reconstruction and handling of data. For example, it has been shown that for at least some cases, sub-pixel alignment of serial sections might be essential to achieve accurate results.Reference Dillon and Rohrer273, Reference Li, Dillon and Rohrer274 This can be seen, for example, by examining the orientation of triple junction lines in an equiaxed microstructure; these should be randomly oriented, with an average orientation parallel to the milling direction. However, triple line orientations from 3D-EBSD datasets, when examined in the sample reference frame, are typically biased; correction requires a sub-pixel rigid offset to the positions in each layer. The development of consensus around reconstruction practices, and their subsequent integration into widely available software packages are essential for the progress of the field.
Like the other characterization methods reviewed in this article, automated serial sectioning has yet to be tapped to its full quantitative potential. One can observe 3D structure and extract grains from the structure to view their shapes, but quantitative analysis of morphological or crystallographic features is still not possible via commercially available software. Many research groups have built software to extract various structural measures, but to date, there has been no coordinated effort to develop the necessary software tools that would enable complete interrogation of the data. A coordinated community effort would accelerate capability advancement as well as application of this technique.
Similarly, 3D-EBSD provides a wealth of quantitative data, and such information can provide deep physical insights to resolve standing scientific questions. For example, detailed examination of the crystallography and energy of various grain boundaries has revealed an inverse relationship between the grain population and the grain boundary energy across many materialsReference Dillon and Rohrer275; the data thus reveal an underlying principle of polycrystalline structures, namely, that the lowest energy grain boundaries are, on average, larger in area and occur with a great frequency than the higher energy grain boundaries. In addition, advances in data analysis, for example, the cross-correlation method, improves the orientation resolution from 0.5° to 0.0061° and the strain sensitivity, allowing measurement of all nine components of the elastic deformation gradient tensor to a resolution of 10−4.Reference Wilkinson, Meaden and Dingley15, Reference Wilkinson, Meaden and Dingley16, Reference Adams and Kacher276–Reference Dingley, Wilkinson, Meaden and Karamched279 With more quantitative analysis of 3D-EBSD, we can expect many other such broadly reaching scientific principles to be uncovered.
III. TECHNIQUE SYNERGY: THE STATE-OF-THE-ART IN CHARACTERIZATION
One significant consensus among the group was that the most fruitful scientific uses of advanced characterization techniques have occurred not when a single technique was used, but when multiple techniques were synergized to provide complementary data. Similarly, the integration of modeling and simulation with characterization tools invariably increases the scientific value of any experimental dataset. During the discussions, the group deliberated upon and identified many examples of technique synergy that highlight this theme. A selection of these examples is reviewed briefly in this section, beginning with studies of static microstructural features (nanoscale clusters, dislocations, and interfaces) and ending with some studies that explicitly focus on the study of microstructure evolution.
A. Technique synergy for the study of microstructural features
1. Nanoscale clustering
One area in which technique synergy has made significant scientific impact in materials science is in the identification of local chemical clusters in alloy systems. Although the control of nanoscale solute clustering has been at the heart of many alloy designs (e.g., in precipitation strengthened or internally oxidized alloys) for decades, the combined use of, for example, APT, TEM-based methods, and scattering techniques has opened new vistas on such classical problems. At the same time, they have paved the way towards understanding the chemical order in complex amorphous alloys.
In the first example, a wide array of characterization and simulation techniques was brought to bear on a new class of oxide dispersion-strengthened ferritic steels, termed “nanostructured ferritic steels.” These materials exhibit remarkable tolerance to displacement damage and possess excellent creep properties at high temperature, making them candidate materials for advanced nuclear reactor designs.Reference Hoelzer, Allinger, Miller, Odette and Bentley280–Reference Miller, Hoelzer, Kenik and Russell282 The alloys in this family are fabricated by mechanical alloying of the metallic components (Fe, Cr, Ti, and either W or Mo and Al) with Y2O3 powder and subsequent consolidation by hot extrusion; this process leads to supersaturation with Y and O during milling, and the formation of a high number density of 2- to 4-nm diameter Ti-, Y-, and O-enriched nanoclusters upon hot consolidation.Reference Schneibel, Liu, Miller, Mills, Sarosi, Heilmaier and Sturm283Figure 25 shows APT data revealing the nanoclusters; these data were complemented by energy-filtered TEM and spectrum imaging. In situ small-angle x-ray scattering revealed that these nanoclusters are remarkably stable during high temperature isothermal annealing up to at least 1300–1400 °C. To understand this unusual resistance to coarsening, first-principle calculations were used to identify a strong interaction between vacancies, oxygen, titanium and yttrium atomsReference Fu, Krcmar, Painter and Chen284; the decoration of nanoclusters with excess vacancies and additional solutes is believed to insulate them against diffusional coarsening. Support for this theory is provided by positron annihilation spectroscopy data, which verifies that nanoclusters are accompanied by vacancy clusters in these alloys.Reference Xu, Liu, Miller and Chen285

FIG. 25. Atom maps of 2–4 nm Ti-, Y-, and O-enriched nanoclusters and Cr, W, and C segregation to grain boundaries in 14YWT. Each dot in these atom maps are a single atom. From Ref. Reference Schneibel, Liu, Miller, Mills, Sarosi, Heilmaier and Sturm283. Copyright Elsevier, reproduced with permission.
The above example is just one of the many, in which APT has been used to study nanoscale atomic clustering and precipitation in the bulk of alloy systems. In many of these studies, the technique is complemented by TEM-based methods to provide quantitative size and shape data on the precipitates. One example that particularly emphasizes the direction of the field in synergizing characterization techniques is provided by the work of Arslan et al.Reference Arslan, Marquis, Homer, Hekmaty and Bartelt286 Because APT samples are necessarily fine needles, they are well-suited geometrically to analysis by tomographic imaging methods. Arslan et al. used STEM tomography and APT on the very same volume of an Al–Ag alloy specimen and used the comparison between the two datasets to study the artifacts of reconstruction in each of them.
The third example of technique synergy in characterizing nanoscale solute clustering deals with the devitrification of bulk metallic glass and combines APT and small-angle x-ray and neutron scattering. Yang et al. studied a cast glass of Zr52.5Cu17.9Ni14.6Al10Ti5, which was partially crystallized to yield a high number density of 10–20 nm particles.Reference Yang, Miller, Wang, Liu, Stoica, Ma, Almer and Shi287 These particles gave rise to a characteristic small-angle neutron scattering profile with a strong interference peak at Q = 0.2–0.3 Å−1, and a similar though less pronounced peak in x-ray scattering experiments. The scattering data were found to be well described by assuming a core-shell structure for the nanoparticles and a log-normal size distribution. The core-shell structure was confirmed by laser-pulsed APT analysis, as shown in Fig. 26, with cores of Zr2M (M = Ni or Cu) and shells of a similar stoichiometry but different composition (M = Ni, Cu, or Al). XRD confirmed the Zr2M intermetallic structure of the precipitates. The rejection of Ti and preferential alloying contents in the core-shell structure also were rationalized based on the various heats of mixing of the components.

FIG. 26. Devitrification of bulk metallic glass of Zr52.5Cu17.9Ni14.6Al10Ti5. (a) Isoconcentration surfaces revealing the lenticular Zr-enriched precipitates and the internal Al-enriched core. Zr, red; Al, yellow. (b) Linear composition profiles through the center of the lenticular precipitate showing the rejection of Al from the Cr while Ti atoms are rejected from both the core and the shell. From Ref. Reference Yang, Miller, Wang, Liu, Stoica, Ma, Almer and Shi287.. Copyright Wiley-VCH Verlag GmbH & Co. KGaA, reproduced with permission.
The study of second-phase precipitation and nanoscale clustering is of course not limited to the bulk of alloys, but also poses significant challenges to surface scientists interested in, for example, film growth, surface phases, and catalysis. For example, Kulkarni et al. used both extended x-ray absorption fine structure (EXAFS) and HAADF STEM to study monosized carbonyl clusters of a heavy metal, Os, on a porous support of MgO.Reference Kulkarni, Mehraeen, Reed, Okamoto, Browning and Gates288 Because of the processing history of the specimen, some of the clusters were decarbonylated and others were not. The radii of the undecarbonylated clusters were found by microscopy to be 3.11 ± 0.09 Å, which agreed well with EXAFS data at 2.94 ± 0.07 Å. By analyzing partially decarbonylated clusters and again finding agreement between EXAFS and STEM, Kulkarni et al. were able to conclude that decarbonylation did not affect the dimensions of the metal frame in the clusters significantly.
2. Dislocations
The mechanical properties of crystalline materials depend upon the dislocation density and its variation with position and history. What is more, dislocation densities are a primary experimental measurable against which crystal plasticity models can be calibrated and tested. With the ever-increasing speed and resolution of EBSD measurements, large field-of-view dislocation density tensor measurements have become routine in 2D (which allows access only to dislocation structures that cause lattice rotations in the plane). As the examples below show, the development of 3D-EBSD and its synergy with and validation against x-ray microdiffraction measurements now puts the field on the brink of having routine access to the full dislocation density tensor in 3D.
As an example, consider the determination of excess dislocationReference Nye289, Reference El-Dasher, Adams and Rollett290 content made on a deformed Cu single crystal by using 2D-EBSD and x-ray microdiffraction techniques.Reference Field, Magid, Mastorakos, Florando, Lassila and Morris291 The same volume of material was probed by both methods. Both techniques yielded a similar distribution of misorientation and even dislocation density. However, the structure as seen by x-ray microdiffraction showed sharp dislocation walls, whereas the structure as seen by EBSD showed a loose tangle of dislocations and diffuse dislocation walls. The difference can be seen by comparing the images in Fig. 27. The angular resolution of the x-ray technique is superior to that of the EBSD measurements by more than an order of magnitude (0.01° compared with 0.5°), but the spatial resolution of EBSD is sufficiently superior (∼10 nm compared with ∼2 μm) that it yields a more detailed view of the relaxed dislocation structures on the polished surface. The impact on the measurement of the dislocation density of extending the EBSD analysis from 2D to 3D was considered by Field et al.Reference Field, Magid, Mastorakos, Florando, Lassila and Morris291 In this work, 1050 aluminum was studied after hot rolling, and a direct comparison of the 2D and 3D dislocation density measurements based on 2D- and 3D-EBSD, respectively, was made, and the result shown in Fig. 28(a) shows an orientation image of a deformed crystallite, while Figs. 28(b) and 28(c) contain gray scale images of the same region showing the spatial variation of excess dislocations as gray scale maps. The average excess dislocation density is on the order of 9 × 1013 m−2 as determined from the 2D measurements, and somewhat higher at 2 × 1014 m−2 when using the full 3D information. Although the gray-scale images do not show the full detail of the dislocation density tensor, there were key differences in the details of the tensor components between the 2D and 3D measurements.
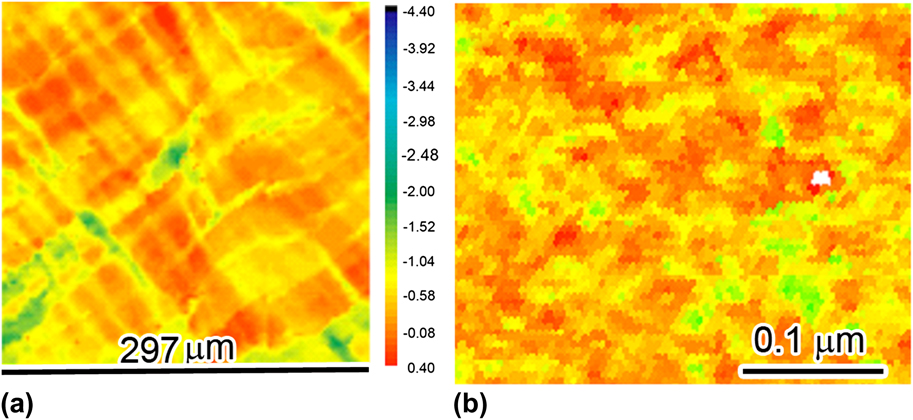
FIG. 27. Orientation images showing the angular deviation from the nominal [2 9 20] orientation of the Cu crystallite before deformation. (a) Image obtained from x-ray microdiffraction, and (b) image obtained from electron backscatter diffraction (EBSD). From Ref Reference Field, Magid, Mastorakos, Florando, Lassila and Morris291. Copyright Taylor and Francis Group, reproduced with permission.

FIG. 28. Deformed commercial purity aluminum showing the (a) orientation image and dislocation density maps obtained from (b) 2D analysis, and (c) 3D information. The scale shown is for dislocation density for both the 2D and 3D analyses. Figure courtesy of D.P. Field.
The evolution of 4D characterization by XRD during mechanical loading has provided new insight to strain evolution and dislocation patterning in a single grain in the interior of the sample. An example of a surprising finding on this topic is the fluctuation in the strain map with increasing strain, which suggested that the dislocation structures were not static but evolve dynamically, forming and annihilating until becoming stable at some higher level of strain.Reference Jakobsen, Poulsen, Lienert, Almer, Shastri, Sorensen, Gundlach and Pantleon292, Reference Jakobsen, Poulsen, Lienert and Pantleon293 This insight hints at collective processes of annihilation and construction, which is contrary to traditional concepts of continuous formation of structures. Digital image correlation as well as thermal dissipation measurements on deformed Zr showed that the deformation microstructure was continually evolving during loading.Reference Padilla, Smith, Lambros, Beaudoin and Robertson294 Similarly, time-resolved deformation experiments in the TEM along with computer simulations have shed new light on how dislocations interact with precipitatesReference Clark, Robertson, Dougherty, Ahn and Sofronis295–Reference Xiang, Srolovitz, Cheng and Weinan298 and other defects.Reference Robach, Robertson, Wirth and Arsenlis299–Reference Wirth, Bulatov and De La Diaz Rubia302 These studies suggest that the simple dislocation–particle interactions described in textbooks for strengthening mechanisms and creep in particle-strengthened systems frequently capture only one of many possible interactions, and that the interaction process can evolve with strain.
The combination of methods outlined in this section provide new insights questioning conventional concepts as to how dislocations interact with other defects and how they determine the mechanical properties of materials. These in combination with the advances in computational tools are providing unprecedented opportunities to model and predict mechanical properties of materials.
3. Interfaces
Many of the most significant problems in materials science pertain to interface composition and structure, and no corner of the field stands to benefit more from the synergy of advanced characterization techniques than does interface science. As the following examples show, technique synergy will have profound impact both on the study of individual interfaces and on the full network of interfaces in polycrystalline solids.
The first example shows a detailed multi-capability study of individual grain boundaries by Taheri et al., who aimed to connect boundary character, mobility, and composition.Reference Taheri, Sebastian, Reed, Seidman and Rollett268 Their work combined EBSD (2D) and APT of select individual boundaries. The alloy studied was an aluminum alloy with principal alloying elements of Cu and Zr. In situ annealing during EBSD analysis permitted direct observation of recrystallization and the identification of specific boundary types with different mobilities. For example, Σ7-type coincidence boundaries were highly mobile, as shown in Fig. 29. To better appreciate why mobility varied between different boundary types, Taheri et al. used FIB machining to prepare site-specific atom probe specimens centered upon individual grain boundaries [Fig. 29(b)], which lay parallel to the needle axis. From their APT work, Taheri et al. observed the presence of both copper and zirconium at general high-angle grain boundaries, but only Zr at coincidence site lattice boundaries. This result presents a large step toward correlating various aspects of interfaces, namely, grain boundary mobility, solute segregation, and character.

FIG. 29. (a) EBSD map showing partially recrystallized grain located away from the nucleation site. Larger, darker grains are of grain boundaries with Σ7 tilt character at their mobile leading edge. (b) Secondary electron image of the specific area containing the Σ7 grain boundary. (c) EBSD inverse pole figure map of the area designated in the box in the center image. (d) Schematic diagram showing the Σ7 grain boundary (plan view) and the location of the Pt “cap” to be applied before milling. From Ref. Reference Taheri, Sebastian, Reed, Seidman and Rollett268. Copyright Elsevier, reproduced with permission.
An example in which TEM, APT, and computer simulations were all necessary to probe the composition of the grain boundary network is provided by the work of Detor et al.Reference Detor, Miller and Schuh303–Reference Detor and Schuh305 They studied nanocrystalline solid solution Ni-W alloys prepared by electrodeposition; in this system, W is known to promote grain refinement, presumably due to W segregation at grain boundaries. Detor et al. specifically explored grain sizes of about 20, 10, and 3 nm, which correspond to non-dilute levels of W ranging from about 10–20 at.%. At these small grain sizes, a single set of APT data comprises many grains and grain boundaries, and the grain boundaries cannot be clearly observed in the APT data. At the same time, TEM can give a sense of the average grain size, but it is difficult to study chemical segregation with TEM-based methods at these very fine scales with samples that necessarily contain many grains through their thickness and with non-dilute solute levels that exhibit low segregation contrast. Accordingly, Detor et al. used Monte Carlo simulations with multibody metallic potentials to prepare an atomistic model of fcc Ni-W with a 3 nm grain size and with W in an equilibrated segregated state at the grain boundaries. With this simulated sample, they verified that statistical analysis of the W distribution could accurately reveal the state of segregation; for example, as shown in Fig. 30(a), the autocorrelation function of W atoms reveals a principle peak at the known grain size of the simulated sample. When the same statistical analysis was subsequently applied to experimental APT data [Fig. 30(b)], the authors were able to establish that W is indeed segregated to grain boundaries even at grain sizes as fine as 3 nm. In subsequent work, Detor et al. considered annealed specimens at larger grain sizes and verified through more direct analysis that W is segregated to grain boundaries in such alloys, as shown in Fig. 30(c).Reference Detor, Miller and Schuh304

FIG. 30. 3D auto-correlation functions for W atoms in nanocrystalline Ni-W with a grain size of ∼3 nm, taken from (a) experimental APT data and (b) atomistic simulations (simulated structure shown in the inset). Through statistical analysis of the APT data and comparison with the simulated structure, it was shown that the average W distribution over all the grain boundaries could be determined. (c) APT data from an annealed sample of somewhat larger grain size (20 nm), where an APT reconstruction artifact highlights the locations of grain boundaries, permitting a more direct measurement of the local segregation at individual boundaries. From Refs. Reference Detor, Miller and Schuh178, Reference Detor, Miller and Schuh303. Copyright Taylor and Francis Group, and Elsevier, reproduced with permission.
B. Technique synergy for the study of damage evolution in materials
1. Radiation damage
Radiation damage is a classical science and engineering problem that can expect major advances in understanding because of the suite of new characterization tools that are available. An example of state-of-the-art experimental work in this area is provided by the work of Was and colleagues at the University of Michigan. They combined the use of TEM, STEM, and APT to study the damage produced in a commercial purity 304 stainless steel alloy and a controlled-purity 304 alloy with increased Si content. These materials were irradiated to 5 dpa at 360 °C using 2 MeV protons. With TEM and STEM, a number of interesting observations were made. For example, dark-field diffraction contrast imaging in the TEM permitted quantitative analysis of faulted (Frank) loops generated during irradiation and revealed second phase particles caused by irradiation, believed to be rich in Ni and Si. STEM analysis revealed significant depletion of Cr, Fe, and Mn at grain boundaries and enrichment of Ni and Si there.
Each of these observations provides some information about the effects of radiation on structure. However, the complementary use of APT to analyze irradiated material provided a wealth of additional quantitative information about these features. For example, the dislocation loops were decorated by segregated Si or Ni- and Si-rich clusters. As a result, dislocation loops could be observed in the APT data; their size (6 nm) matched the quantitative measurement obtained from loop size measurements made on electron micrographs (5.7 nm). Figure 31 shows the APT data for an irradiated sample with excess Si content, revealing the distribution of Ni- and Si-rich clusters. As evidenced by the lack of overlap between the contours of 45 wt% Ni (a) and 15 wt% Si (b), the Ni and Si content vary from one particle to another (Fig. 32). Figure 32(c) shows a high magnification image of a Ni- and Si-rich cluster along with a composition profile, showing that although the enrichment of Ni and Si extends to ∼10 nm, only the ∼2 nm core of the cluster approaches the stoichiometric composition of the expected intermetallic (Ni3Si). Compared with this specimen, a stainless steel of lower Si concentration contained even fewer clusters that reached the composition of Ni3Si.
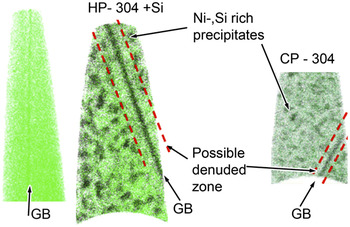
FIG. 31. Distribution of Ni and Si in HP-304, HP-304 + Si, and CP-304 irradiated to 5 dpa at 360 °C. Ni- and Si-rich clusters are indicated by arrows in HP-304-Si and CP-304. Possible denuded zones are indicated by dashed lines. Ni is shown in green and Si in gray. Figure courtesy of G. Was.
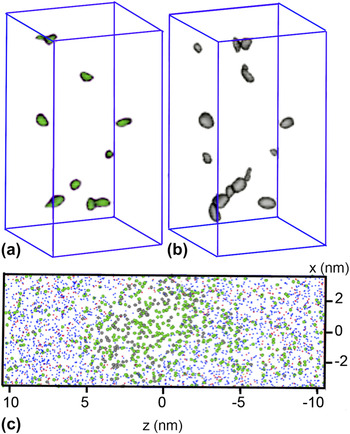
FIG. 32. Isosurface of (a) Ni at 45 wt% and (b) Si at 15 wt% in alloy HP-304 + Si irradiated to 5 dpa at 360 °C. The box is 40 nm × 40 nm × 70 nm. (c) Magnified image of a Ni- and Si-rich cluster in alloy HP-304 irradiated to 5 dpa at 360 °C. Figure courtesy of G. Was.
It is well known that irradiation causes compositional modifications at grain boundaries. STEM analysis of grain boundary composition, while quantitative, is not sufficiently sensitive to all elements. APT was used to characterize the composition of grain boundaries in the irradiated condition, yielding the data shown in Fig. 33. Both APT and STEM revealed grain boundary segregation of Ni and Si and showed excellent agreement in the magnitude and profiles of Ni, Cr, Mn, and Si. However, APT revealed B and P segregation that could not be resolved in STEM. The concentration of P at the grain boundary was about 15 times higher than in the bulk and B was more than 200 times higher after irradiation. This compositional modification has important implications for understanding the degradation in the mechanical properties of irradiated materials

FIG. 33. Composition profiles of minor elements (B, P, C, and S) across a grain boundary in alloy CP-304 irradiated to 5 dpa at 360 °C as characterized by APT. Figure courtesy of G. Was.
In analyzing damage evolution in materials, time-resolved measurements are obviously highly desirable. The attachment of an ion-accelerator to an electron microscope has enhanced the understanding of long-term damage evolution from displacement cascades as well as the evolution of the damage microstructure under prolonged irradiation in metals and semiconductors.Reference Birtcher, Kirk, Furuya, Lumpkin and Ruault306–Reference Jenkins, Yao, Hernandez-Mayoral and Kirk308 When direct experimental data on the structure evolution is lacking, there is an important opportunity for simulations to provide fundamental insights. An example of this is provided by the work of Misra and co-workers,Reference Demkowicz, Hoagland and Hirth309–Reference Misra, Demkowicz, Zhang and Hoagland312 who studied radiation damage in nanolayered composites with structural wavelengths on the order of a few nanometers. Figure 34(a) shows an under-focused bright-field TEM image of a helium ion–irradiated (150 keV, 1 × 1017 cm−2) nanolayered composite of Cu and Nb, with a 5 nm structural repeat length. At this dose, no helium bubbles, stacking-fault tetrahedra, or interstitial loops were detected, and the compositional sharpness of the Cu/Nb interfaces was retained. At higher helium doses (35 keV, 1.5 × 1017 cm−2), ∼1–2 nm diameter helium bubbles were resolved in defocused bright-field TEM images [Fig. 34(b)]. At higher temperatures, these bubbles can grow in situ during irradiation; at 500 °C, diameters of 20–50 nm were observed in a very coarse multilayer. However, in the 5 nm multilayer, the bubble size in the Cu layer is on the order of the layer thickness, indicating that bubble growth is arrested by the interfaces.

FIG. 34. Comparison of the damage structure produced in Cu-Nb multilayers following implantation with (a) 150 keV He ions to a dose of 1 × 1017 cm−2 at room temperature and (b) 33 keV He ions to a dose of 1.5 × 1017 ions cm−2. From Ref. Reference Misra, Demkowicz, Zhang and Hoagland312 Copyright JOM Journal of the Minerals, Metals and Materials Society, reproduced with permission.
These experimental data show that interphase interfaces act as sinks for radiation-induced point defects and solute atoms such as helium. To better appreciate the specific mechanisms underlying this effect, complementary atomistic simulations were used. Specifically, they showed that in the copper–niobium system, the interface structures exhibit multiple atomic arrangements with nearly degenerate energies. Thus, when a vacancy or interstitial is absorbed in the interface, locally the atomic arrangement can change from one structure to another, providing a means of temporarily storing defects until they can recombine (restoring the interface to its original configuration). Furthermore, the defect formation energy at an interface is significantly lower than in the bulk and a defect core gets delocalized at the interface, thereby increasing the distance over which a vacancy and an interstitial can recombine spontaneously. Taken together, the experimental characterization of irradiated samples and the atomistic modeling provide a sound physical picture for the damage evolution process in Cu–Nb multilayers and point to design principles for radiation-resistant materials.
2 Stress-corrosion cracking
The characterization approach to the classic problem of stress-corrosion cracking (SCC) has been revolutionized in recent years. Indirect methods, in which large-scale measurements are used to infer local details of corrosion behavior or crack propagation, are now being augmented by direct measurements that reveal the actual details of the microstructure and local composition over multiple length scales. The science of SCC thus stands to undergo dramatic expansion and revision in the coming years, entirely as a consequence of using a synergetic combination of characterization techniques.
An example of this strategy is provided by the work of Lozano-Perez et al. to understand the effects of cold work in SCC of 304 stainless steel; cold working is known to increase the crack growth rate in pressurized water nuclear reactors under primary water conditions, but the mechanisms that control crack propagation are unclear.Reference Lozano-Perez, Yamada, Terachi, Schroder, English, Smith, Grovenor and Eyre313–Reference Lozano-Perez, Rodrigo and Gontard319 Cold-worked samples are harder, have measurably different corrosion properties, and exhibit a complex microstructure with a high density of so-called twin deformation bands, which have a complex internal structure where sub-cells and dislocation bundles are frequently observed. The density of bands is dependent on the level of cold work. However, localized regions with high dislocation densities appear from the very early stages of deformation. These bands, as revealed by 3D microstructural analysis by FIB-based serial sectioning, oxidize to depths of about 1.5 μm from the nearest free surface (Fig. 35).Reference Lozano-Perez, Rodrigo and Gontard319 APT analysis of the surface oxide showed that it was composed of two layers, the inner layer was a Cr-rich spinel and the outer layer was a Fe-rich spinel (not included in the APT reconstruction shown in Fig. 36).Reference Lozano-Perez, Saxey, Yamada and Terachi318 The inner Cr-rich surface oxide is clearly visible at the top of the sample [Fig. 36(a)], and a volume containing the interface with the metal is shown in detail in Fig. 36(c) together with a concentration profile [Fig. 36(d)]. The most interesting findings, however, are a series of Cr-rich oxide intrusions below the oxide/metal interface, which can be seen in Fig. 36(a) and from the top (with the Cr-rich spinel cap removed) in Fig. 36(c). These oxide pockets, with sub-stoichiometric compositions, are associated with the defects caused by the earlier cold working (e.g., dislocations). Furthermore, Li, an additive to the cooling water in the nuclear reactor, was revealed for the first time to be incorporated in the growing Cr-rich oxide. High-resolution STEM imaging of the crack tip region confirmed that the deformation twins, and its associated high-defect densities, are preferential sites for oxidation. Oxidation rates were found to be higher than on the free surface, suggesting that they were stress assisted.Reference Lozano-Perez, Yamada, Terachi, Schroder, English, Smith, Grovenor and Eyre313 Finally, electron tomography was used to reconstruct a 3D volume containing a crack tip and all the relevant microstructural features around it. As can be seen in Fig. 37, the crack was arrested between regions with high deformation twin band density and opened considerably through plastic deformation of the top grain. Only the presence of diffraction contrast enabled the representation of the deformation twin as planes in 3D in the reconstruction [see Fig. 37(b)]. Reference Lozano-Perez, Rodrigo and Gontard319 Such microstructural details are of particular interest to fully understand the stresses in the sample and the interaction of the crack tip with these microstructural features.

FIG. 35. Reconstructed volume showing the open crack (dark) and the oxidized twin deformation bands (light), together with one of the original slices. Sample: 304SS with 20% CW. From Ref. Reference Lozano-Perez, Rodrigo and Gontard319. Copyright Elsevier, reproduced with permission.
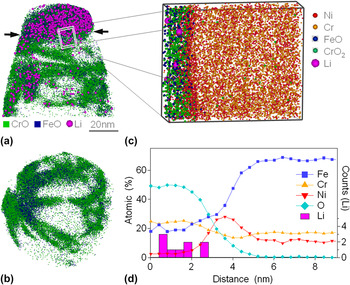
FIG. 36. (a) APT reconstruction showing the presence of lithium atoms within the cap and sub-interface oxides. (b) Top-view of the sub-interface region showing the distribution of oxides (cap oxide removed; only oxide species shown). The oxide regions beneath the cap are interconnected. (c) Sub-volume taken from the cap-oxide-to-metal interface showing selected species. (d) Concentration profile across the oxide–metal interface generated from the region in (c). The presence of lithium is represented by an atom-count because its concentration is very low. From Ref. Reference Lozano-Perez, Saxey, Yamada and Terachi318. Copyright Elsevier, reproduced with permission.

FIG. 37. (a) STEM HAADF image showing the crack tip used for the tomographic reconstruction. The high dislocation density and the location of several TDBs in the bottom grain are clearly visible; (b) 3D reconstructed volume representing all relevant features. Sample 304SS with 5% CW. From Ref. Reference Lozano-Perez, Rodrigo and Gontard319. Copyright Elsevier, reproduced with permission.
IV. GRAND CHALLENGES FOR MATERIALS CHARACTERIZATION IN 4D
In the course of their deliberations and discussions, the group identified major research directions that warrant focused attention in the coming decade. These “grand challenge” problems span instrumentation advances from general materials science questions of broad generality to specific engineering problems that demand extreme characterization of materials. In this section, we provide a short summary of these problems with the hope that these ideas will inspire new efforts.
A. Grand challenges in instrumentation
Although the specific development trajectories of each family of characterization methods were presented in Section II, a few broader challenges to the instrumentation community were identified. Several notable gaps in the characterization landscape are in need of focused attention in the coming years and these are outlined in this section.
1. Direct observation of atomic processes
There are no techniques presently with simultaneous sub-Ångström spatial resolution and picosecond temporal resolution, and yet these are the scales associated with atomistic mechanisms that underlie the most pressing problems in materials science. For example, diffusion mechanisms are accessible indirectly through inference or simulation,Reference Nishimura, Kobayashi, Ohoyama, Kanno, Yashima and Yamada320 whereas direct atomic-scale observation of such processes would propel the field forward in a giant leap. Apart from atomic dynamics on crystal lattices, major problems in interface diffusion and mobility, dislocation dynamics, glass rheology, and diffusion in amorphous materials all stand to be resolved if such a technique could be developed. Problems in damage evolution often involve the production, migration, and interaction of point defects on these scales and also await a method of direct observation. One can envision the development of, for example, next-generation DTEM with simultaneous spatial and temporal resolution that will make it possible to study point defect dynamics. Because of the accessibility of these scales with atomistic simulation methods, it is also possible to envision closely coupled experiments and models (in a manner similar to reverse Monte Carlo interpretation of experimental signals) that together provide insight on such processes.
2. Mapping of crystallographic information at the nanoscale
The tremendous impact of EBSD directly demonstrates the value of mapped crystallographic information, which provides insight on processing history, structure–property relationships, interfaces and interfacial networks, local plastic strain distribution, and phase structure. The transition of EBSD into a 3D technique and the emergence of complementary methods like 3D-XRD provide a clear evolutionary trajectory for the coming years. However, the limited spatial resolution of these methods leaves a substantial gap in the characterization toolbox, and there is a pressing need for the ability to map crystallographic orientation information with nanometer or even sub-nanometer resolution. Crystallographic information about individual nanocrystals, dislocation networks, and other complex features with nanometer-level detail are not accessible presently, except through traditional electron diffraction analysis, which is conducted manually. Recent years have seen significant development of automated crystallographic mapping routines in the TEMReference Rauch, Véron, Portillo, Bultreys, Maniette and Nicolopoulos321; the refinement and wide dissemination of these techniques is a significant challenge that can fill an important niche of broad applicability across the physical sciences.
3. Mapping of hydrogen
Many problems of technological and scientific importance rely upon knowledge of the distribution of hydrogen in materials; metal embrittlement, corrosion, SCC, hydrogen storage, catalytic surface processes, local impurity doping in semiconductors, and organic materials analysis represent a few specific examples. And yet today there is no established technique capable of mapping hydrogen at the nanometer length scales, especially in 3D. This shortcoming is attributable to detecting hydrogen at above background levels in analytical instruments and to the high mobility of the species. Some efforts have been made to explore hydrogen mapping with APTReference Gemma, Al-Kassab, Kirchheim and Pundt322–Reference Takahashia, Kawakamia, Kobayashia and Taruib324 or with EELS,Reference Kihn, Mirguet and Calmels325 but these are not widely accepted and in the current form are not applicable to all materials of interest. The development of a more robust and generally applicable capability would enable studies of hydrogen in a number of key technologically important areas.
4. Mapping of free volume
Excess volume, or free volume, is a nebulous feature of many microstructural elements, most notably dislocations, grain boundaries, and triple junctions. Their free volume content can be critical to their ability to act as vacancy sources or sinks, to their mobility, and to the pressure-dependence of properties that depend upon them. What is more, free volume is appreciated as perhaps the most important state variable controlling the properties of amorphous materialsReference Schuh, Hufnagel and Ramamurty326 and is of increasing interest in understanding the state and properties of grain boundaries in nanostructured materials.Reference Detor and Schuh305, Reference Vo, Averback, Bellon and Caro327 Unfortunately, a systematic tool to measure local excess volume associated with such features is lacking. Advances in high resolution TEM and so-called fluctuation microscopyReference Treacy, Gibson, Fan, Paterson and McNulty328 provide some steps towards resolving this complex problem, but have not yet reached the level of sophistication needed to address the free volume distribution as a key factor in structure–property connections or to study its evolution in real time. It is, therefore, a grand challenge to the field to develop a robust tool that can measure atomic density with nanometer-scale resolution in general atomic environments.
5. Automation and software
Across all the varied and diverse characterization methods discussed here, there is an overarching need for standardization of experimental methods and data analysis. For many of the techniques, the scientist remains actively involved in the data acquisition process; while this leads to improved quality with present instruments, it also introduces numerous uncontrolled variables and inevitably leads to variability across research groups and instruments. The trend towards automation of these techniques can address this issue; automated experimentation necessarily leads to standardization of accepted regimens. Similarly, better software tools are needed for handling the invariably large volumes of data that are associated with new characterization tools. This need includes software for archiving data in a readily accessible format, including the raw data for future re-processing in the likely event that better post-processing data software is later developed. The introduction of automation and standard software packages can also lead to discussions of data sharing protocols; the most efficient global materials research enterprise may be the one in which such data sets are broadly available to the entire community.
B. Grand challenges in the characterization of interfaces
Among the many microstructural features that can be characterized by the techniques in this study, interfaces offer the largest set of scientific questions that remain unanswered. With the improved resolution and field-of-view of today’s characterization toolbox, interface and surface science stands on the cusp of a major revolution. A number of grand challenges around interfaces were identified and these ranged from the level of individual interfaces to complex collections of interfaces in solid materials.
1. Perfect-fidelity reconstruction of a general interface
Virtually every technique reviewed in this article has been used to characterize interfaces, although in every case there are limitations to the characterization. For example, APT provides a view of interface chemistry, but with known artifacts and without providing knowledge of the interface crystallography. Similarly, TEM-based methods are usually restricted to a single view on boundaries with special symmetries. A near-term grand challenge for the field is to link all the available techniques together to completely characterize the nature of a single, general interface of no specific symmetry and to chemically identify each and every atom and its actual spatial location (in 3D) at a general interface. Such analysis would provide complete detail about the sites for solute segregation, excess free volume, as well as extrinsic and intrinsic dislocation content. Several of the instruments discussed in this article, when properly combined, are at the edge of being able to provide this level of quantification. For example, if APT detection efficiency could be improved to 100%, interface reconstructions could be validated and precisely corrected through quantitative comparison with atomic-resolution TEM tomography, using site-specific samples prepared by FIB.
2. High throughput mapping of interface properties
A second grand challenge for interface science is to move from high-fidelity characterization of individual interfaces to characterization and mapping of structure and properties across the full multi-dimensional spectrum of possible interfaces in a given system. For grain boundaries in single-phase materials, this corresponds to the characterization of five macroscopic degrees of freedom comprising the misorientation as well as the orientation of the boundary plane normal. For multiphase materials or materials without centrosymmetric point symmetries, the dimensionality of the space is even larger. The challenge of mapping these multidimensional interfacial character spaces is thus one of scope requiring systematic sampling over many interfaces, the vast majority of which are not of special symmetry. Although crystallographic stereologyReference Bunge and Schwarzer329–Reference Larsen and Adams331 and 3D-EBSD9 have permitted characterization of the spectrum of boundary types that exist within polycrystals, direct measurements of local boundary properties across this space are extremely rare as yet. The problem is, therefore, more complex and involved than simply preparing and systematically examining interfaces over this large continuum; rather, local property measurements are required at each point in the multi-dimensional space. Interfacial mobility, segregation and diffusion coefficients, resistance to cracking, slip transfer, sliding, conduction, and corrosion are all properties that are poorly mapped as a function of the interface character. Perhaps, the simplest boundary properties to access are those amenable to straightforward analysis via geometric or surface-analysis techniques. For example, local corrosion potentials at grain boundaries could be mapped periodically on select 2D slices during a serial sectioning procedure using electrochemical microscopy or atomic force microscopy after chemical etching. A far greater challenge is posed by properties that depend in detail on the atomic structure at local boundaries. For example, mapping the local segregation potential for solutes as a function of interface character does not seem tractable merely by combining the characterization tools available at present because the scales mismatch significantly. Although boundary character of a large collection of interfaces may be attained by 3D-EBSD or 3D-XRD methods, the problem of simultaneously acquiring atomic-level segregation information at each boundary (via ATP or electron microscopy-based spectroscopy techniques) appears essentially impossible. In this regard, improved overlap in the field-of-view of these techniques presents a significant roadblock to progress. Perhaps a more likely solution would be the emergence of a mesoscale method for orientation mapping in the TEM which, when combined with a chemical mapping method in the TEM, could address simultaneously both key elements of the problem.
3. Interface networks
Another significant challenge is posed by interfacial properties that are influenced strongly by the ensemble behavior of the interface network. For example, grain boundary sliding is decidedly a local property of each individual boundary, but is influenced by mechanical constraint from the surrounding grains, boundaries, and triple junctions. Similarly, interfacial cracks have stress fields that experience microstructure at some distance. Grain boundary mobility is a local property, but boundary motion in an ensemble of grain boundaries is much more complicated than a simple superposition of individual boundary mobilities. The effects of near-neighborhoodReference Schuh and Frary332, Reference Kumar, King and Schwartz333 as well as long-range network propertiesReference Frary and Schuh334–Reference Schuh, Kumar and King337 are appreciated in a qualitative sense, but quantitative assessment of ensemble properties and their connection to local interfacial properties remains a largely open topic of great importance for many fundamental materials evolution problems. With advanced characterization techniques such as 3D-XRD, it is now possible to study nondestructively the motion of interface ensembles and correlate such properties as local mobility to neighborhood. Modeling studies have pointed out the importance of long-range connectivity among boundaries of different character in several contexts, including diffusion,Reference Schuh and Ying338 creep,Reference Chen and Schuh339 and cracking,Reference Van Siclen340 but such studies provide, for the most part, early qualitative indications of such effects. A grand challenge for interface science is thus to successfully bridge characterization tools to understand complex collective effects among an ensemble of interfaces of varied character.
C. Grand challenges for the engineering science of materials degradation
In the realm of materials damage, characterization tools must provide details not only on specific microstructural features but also on their evolution with time and exposure to a stimulus. Many materials damage problems involve mechanisms that span orders of magnitude in spatial and temporal scales. What is more, these damage processes are often at the heart of technological problems with large economic and societal costs. The engineering science implications of materials characterization in 4D as it pertains to some of these problems as well as the challenges that should be addressed were considered.
1. Radiation damage
Despite decades of research, radiation damage in complex materials is still a topic comprising many unanswered questions. These are of vital interest not only for lifetime prediction and materials selection in contemporary engineering situations, but also for future materials needs in, for example, next-generation fission reactor cores or fusion reactor first walls. Additionally, radiation is now perceived as an interesting potential tool to restructure matter, both in the bulk and during deposition, to create nonequilibrium microstructures with enhanced properties. The key challenge in this space is to understand the defect clustering process in materials subjected to irradiation, as these clusters ultimately drive the damage. These advances will only be achieved by elucidating the atomic- and molecular-level mechanisms of defect production and damage evolution triggered by single and multiple energetic particles and photons interacting with solids and to follow the temporal evolution of the damage state over many orders of magnitude. A range of extreme photon and particle fluxes, including advanced photon and particle-beam sources, must, therefore, be coupled with the modern characterization toolbox. In particular, time-resolved characterization techniques are critical to understanding the kinetics and time evolution of defect aggregation, annihilation, and absorption. Accordingly, the improving spatial resolution and pulsed-time functionality of intense light and neutron sources create opportunities to image the formation of atomic and nanoscale defects as they are created. High-resolution TEM coupled to an ion accelerator can also provide real-time tracking of defect cluster initiation and growth. Development of an in situ ion irradiation capability in a TEM with spatial resolution of sub-Ångström and temporal resolution in the nanosecond range could elucidate experimentally the physics of interaction of radiation-induced defects at interfaces. Mechanisms involving emission of interstitials from grain boundaries to annihilate vacancies near boundaries may occur at nanosecond time scales as revealed by recent molecular dynamic computer simulations,Reference Bai, Voter, Hoagland, Nastasi and Uberuaga341 but cannot be verified currently due to lack of spatial and temporal resolution in in situ ion irradiation experiments in TEM. Radiation also induces local compositional changes that can be detected with APT, although synergy of APT with other in-situ methods will be required to develop a full time-resolved view of the process.
2. Corrosion
The degradation of material surfaces in chemically active environments is another topic where time-resolved characterization is viewed as critical to understanding existing materials performance and also in designing materials with superior corrosion properties. Corrosion problems occur in environments that render the material thermodynamically unstable, where stability is frequently governed by protective surfaces, such as oxides, sulfides, etc. The stability and permeation resistance of these films are a function of the temperature, pressure, type, and concentration of chemical species in the environment, as well as material composition phases, microstructure, deformation, imposed electrical potential or radiation, and other factors. A significant concern with ex-situ characterization, therefore, is that upon removal of a sample from the stimulus environment, the character of the surface film may evolve. Thus, fundamental knowledge of reaction dynamics and film stability in such environments is still lacking, and ex-situ characterization is considered unlikely to yield a deep understanding. In situ techniques based on time-resolved TEM, spectroscopy, XRD, etc. can provide complementary information on the oxidation process over different length scales. The present challenge for the field is to develop the capability to conduct such synergetic characterizations in realistic environments (involving high temperature, pressure, corrosive medium, and radiation).
3. Nucleation of life-limiting defects in structural materials
Although the basic mechanisms that underlie most mechanical failures (e.g., ductile rupture in overload conditions, or fatigue cracking in cyclic loading conditions) are known, these failure mechanisms are often responsive not to the average microstructural state but to extreme states at specific locations within a material. Nucleation of the life-limiting flaw is poorly understood, although nucleation may comprise a significant fraction of the component’s lifetime. The nucleation event in this context may pertain to dislocation source activation that marks the onset of plastic flow, crack initiation from a microstructural feature, or nucleation of the first void that precedes rupture. It is a grand challenge in understanding mechanical damage to study such nucleation events and learn to identify a priori regions within a microstructure that are susceptible to them. In the case of plasticity, the heterogeneous nucleation of dislocations at interfaces, surfaces, grain boundaries, and on existing dislocation networks is beginning to attract focused study, most of which is simulation-based; complementary 4D characterization tools must be plied to characterize dislocation networks in 3D as they evolve under an applied load. In the case of fatigue cracks, the literature establishes empirically that orientation, microstructure, and chemical environment all influence crack nucleation; 4D characterization methods may reveal how decohesion, delamination, or perhaps the accumulation of excess volume produces a crack that will limit the lifetime of a material. The microvoid coalescence mechanism of ductile rupture, while reasonably understood at low strain rates, remains mysterious under extreme conditions such as shock loading; 4D characterization of this process requires ultrafast analysis methods commensurate with the timescales of the shock itself.
4. Degradation at high temperatures
When elevated temperatures are involved, materials damage is often related to structural evolution, phase changes, coarsening, and their effects on properties. The challenge of characterizing damage evolution (corrosion, cracking, creep) in an evolving structure at high temperatures is certainly a grand one, but many critical energy technologies are limited by such considerations, especially those involving turbines. The materials used in such environments display microstructural complexity spanning multiple length scales. At the nanometer scale, there are problems of coarsening and rafting of nanoscale precipitates, complex solute segregation patterns at grain boundaries, phase interfaces, and dislocations, and nucleation and growth of topologically close packed phases. At the microscale there are casting and processing defects such as freckles or interfacial problems associated with engineering coatings at the surfaces. At even larger (super-millimeter) scales, there are additional issues of macro-chemical segregation due to the solidification process and complex residual stress patterns at the component level. The level of understanding of all these issues is sufficient for engineering design in many cases, but future advances in materials design require a more holistic and scientific understanding of these complex issues and how they interact. To this end, the full suite of current analytical methods must be applied synergistically, with considerable emphasis on in situ measurements in hostile and complex environments.
V. CONCLUSIONS: THE GRANDEST CHALLENGE
It is an exciting time to be a materials scientist; the many parallel advances in characterization that have been made in the past decade have opened new vistas on material structure, its origins in processing, its evolution with time, and its effect on properties. These characterization advances foreshadow a period of rapid growth in the discipline, in the depth of our scientific understanding, in our engineering capacity to mitigate materials damage, and in our ability to design, control, and manipulate the structure of a material to evoke unique properties. The grand challenges posed in Section IV reflect this optimistic expectation; we propose that nothing less than complete understanding of complex microstructures and their 3D spatial and temporal evolution should be the aim of the field in the coming decade.
An overarching conclusion is that materials characterization is a complex landscape of complementary capabilities, and all these are essential for resolving the multifarious time and length scales associated with materials structure. The most exciting advances in characterization to date have occurred when more than one technique was applied to provide complementary sets of data on a single feature or phenomenon. Nonetheless, the synergy among techniques presented in Sec. III is still only at the proof-of-concept level at this point. In light of this, it was proposed that now is the time for “big thinking” in technique synergy; as each characterization technique continues to advance, significant effort should be focused on integrating them together.
The question of how to achieve “extreme technique synergy” is one that is best addressed by the field through the creative activity of individuals and their interaction through collaboration and scientific exchanges. Some possible directions for extreme technique synergy were discussed. For example, the development of dedicated integrative characterization facilities that combine today’s capabilities in new ways. Specific examples might include the following:
(1) In situ electron microscopes comprising multiple columns suited to different techniques, permitting time resolution from the picosecond to super-millisecond scales
(2) An APT apparatus incorporating rapid, high-resolution TEM tomography to perfectly reconstruct the position of every atom in the evaporation sequence
(3) Dramatically accelerated time-resolved radiation tomography (electron, neutron, and x-ray) using two or more crossed-axis beams working in unison to provide complementary views of the same specimen.
Many other examples of a similar flavor were discussed at the workshop and many more can be envisioned.
Another clear direction for extreme technique synergy that is needed across the full spectrum of material science is the concept of “multiscale characterization.” Just as computational materials scientists developed the multiscale modeling paradigm when faced with multiple techniques at disparate scales, characterization scientists must now proceed to develop coordinated research programs that seek to address characterization as a multiscale problem. One opportunity would be to identify and focus on “hot spots” or “weak links” in a complex structure through the coordinated passing of characterization information from one scale to the next: neutrons at the component level, 3D XRD at the microstructural level, FIB-based local specimen preparation for in situ TEM, and APT analysis at the nanoscale. At each scale, the characterization data are used to focus on a smaller volume for analysis by the next method in the sequence. Many other multiscale paradigms can be envisioned, but it seems clear that many problems in the physical sciences span orders of magnitude in length and time scales, and coordination across both scales is a necessary next step for the field.
Although these proposals in “extreme technique synergy” are recognized as monumental, they represent a challenge more to the political and organizational mettle of the field than to our engineering abilities. In this light, it is hoped that this report will inspire thought, organization, and activity toward the vision of perfect-fidelity material characterization in 4D.
ACKNOWLEDGMENTS
This report was sponsored by the Council of Materials Science and Engineering of the U.S. Department of Energy, Office of Basic Energy Sciences. The authors thank Dr. Linda Horton and Professor Frances Hellman for their support. IMR acknowledges the support from Department of Energy BES under grants DE-FG02-07ER46443 and DE-FG02-08ER46525 for preparing this report. CS acknowledges the support from the National Science Foundation under grant DMR-0855402.







































